基于EDEM的带状深松全层施肥铲作业参数优化与试验

刘立晶 马 超 刘忠军

(1.中国农业机械化科学研究院， 北京 100083； 2.土壤植物机器系统技术国家重点实验室， 北京 100083)

0 引言

施肥方式是影响玉米产量的重要因素之一[1]，我国大多以人工表层施撒化肥，分期或者一次性撒施为主，一次性施肥容易造成前期烧种和后期脱肥，分期施肥费时费力且肥料利用效率低下[2]。我国面临着增肥不增产、土壤养分累积过多和化肥使用量过大等问题。深松可有效改善土壤结构、降低犁底层土壤容重、提高土壤中营养物的利用率和土壤的蓄水保墒能力，继而促进作物根系生长，提高作物产量。带状深松全层施肥耕作技术是保护性耕作的一种，是优越性比较突出的保护性耕作技术，是免耕、精耕、深松、精准施肥的结合体。这种耕作对土壤表层的扰动不到2/5，深松带状耕作兼顾了免、耕、深松的同时又兼顾了精准施肥。所以全层深松施肥对提高化肥利用率、减少环境污染具有重要意义[3]。

全层施肥将肥料一次性施入不同土层中，既可以提高肥料利用率，又减少作业次数。文献[4-5]对一次性深施、一次性浅施和分层施肥做了对比研究，发现分层施肥的玉米产量明显高于另外两种情况。文献[6]认为连年免耕会使肥料困在表层土壤中，极易造成烧种、烧苗，后期出现倒伏情况，分层施肥可以改善免耕播种这一弊端。文献[7]认为与常规的施肥相比，采用条带深松方式深施缓释肥的氮肥利用效率和干物质积累量显著增加，有利于根系下扎和提高根系活力。文献[8]研究认为采用深松全层施肥的方式在消耗最少水量的前提下获得较高的产量、水分利用效率和肥料生产能力。

文献[9]设计前后布置的施肥开沟器实现分层施肥。文献[10-11]设计了一种施肥量可调式分层施肥器，并利用离散元法对肥料颗粒的运动规律以及影响施肥配比的主要因素进行了仿真研究。文献[12]研制了一种分层施肥铲，浅层施肥平均深度为11.8 cm，深层施肥平均深度为19.5 cm，并通过试验证明采用此施肥方式对玉米的生长具有明显的促进作用。文献[13]经过对采用分层施肥后玉米生长及养分迁移的研究发现，玉米普通肥50、100、150 mm 3层施肥处理较1层、2层、混施处理利用率显著提高，最底部肥料所占比例应较大，有利于根系的吸收。总体看全层施肥研究集中在全层深松施肥铲结构设计和玉米生长过程两方面，对全层深松施肥铲的工作参数研究较少。

本文设计一种应用在带状免耕播种机上的玉米深松全层施肥铲，对其结构参数进行计算，同时利用EDEM对部件作业过程和作业效果进行仿真分析，研究工作速度和作业深度对全层施肥效果的影响规律，得出最优工作参数组合，并进行田间试验验证。通过对全层深松施肥铲工作参数的研究，进一步提高现有机具的作业性能。

1 带状深松全层施肥装置总体结构设计

1.1 结构示意图及工作原理

如图1所示的带状深松全层施肥装置主要由固定架、四连杆仿形总成、后支架、全层深松施肥铲、整地圆盘、碎土机构等组成。

该装置挂接在播种机前梁上，机器作业时，对土壤进行疏通，深松的同时进行全层施肥作业，再由碎土机构将土块细碎，整平土壤表面，为后续的播种单体作业提供一条清洁种带。

1.2 关键部件

1.2.1总体结构

全层深松施肥铲整体结构如图2所示，主要由深松铲、铲柄、铲尖、输肥管、施肥管和施肥板等组成。

1.2.2工作原理

工作时，深松铲疏松下层土壤并开出肥沟，肥料颗粒经输肥管进入施肥管，在重力作用下沿着施肥管管壁下滑，依次经4个出肥口流出，分别落入不同深度土层中，完成全层施肥作业。

2 关键零部件结构设计

2.1 深松铲结构设计

根据土壤动力学模型，深松铲的受力部分包括铲尖和铲柄两部分[14-21]。

2.1.1铲尖受力分析

深松铲铲尖的受力情况如图3a所示，土壤主要受剪切力的作用，依据图中受力分析可以得到铲尖前进方向上的平衡方程为

Fz=N0sinδ+μ1N0cosδ+Fb

(1)

式中Fz——牵引力，N

N0——铲尖斜面所受的法向载荷，N

μ1——土壤与铲尖的摩擦因数

δ——铲尖入土角，(°)

Fb——土壤对铲尖的阻力，N

作业过程中，土壤的切削力很小，当遇到较大土块、根茬或硬物时，切削阻力明显增大，通常情况下，土壤对铲尖的作用力可以忽略不计，因此铲尖上部土块的受力分析如图3b所示，土块在水平方向与竖直方向上的平衡状态方程为

N0(sinδ+μ1cosδ)-N1(sinδ1+μcosδ1)-
(Fc+Fg)cosδ1=0

(2)

G-N0(cosδ-μ1cosδ)-N1(cosδ1-μcosδ1)+
(Fc+Fg)sinδ1=0

(3)

(4)

式中G——土块重力，N

N1——土块前失效面的法向载荷，N

Fg——土壤加速力，N

Fc——土壤内聚力，N

μ——土壤内摩擦因数

δ1——土块前失效面的倾角，(°)

m——被加速的土壤质量，kg

v——被加速的土壤速度，m/s

tg——加速时间，s

在工作过程中，牵引力与土壤阻力是一对平衡力，结合式(1)～(3)解得

(5)

为简化式(5)，令

(6)

可得

(7)

式中Fz1——土壤阻力，N

土块的前剪切失效面积Sa和土块前失效面的倾角δ1取决于铲尖入土角δ[22]，又根据式(7)可知，当工作速度一定时，即Fg恒定，因此土壤阻力Fz1主要与铲尖入土角δ有关。入土角δ是影响深松铲入土性能的重要因素，入土角δ主要影响深松铲的入土性能和前进阻力，随着入土角的增大，入土能力变差，且阻力增加；入土角减小，疏松土壤效果变差。参考《农业机械设计手册》有关深松铲入土角δ的设计[23]，δ确定为23°。

入土隙角∂为地面与深松铲底面的夹角，如图4所示。入土隙角∂的存在便于深松铲入土，通过试验和文献[24-25]，∂取10°。

2.1.2铲柄曲线设计

为了减小作业过程中的阻力，开沟阻力随着工作速度递增，经研究发现，指数型曲线相较于直线、抛物线减阻效果更优[26-28]，因此铲柄入土部位的线型选择指数型，建立如图5所示的直角坐标系。取入土点A坐标为(x1、y1)、滑切曲线终点B坐标为(x2，y2)。

设滑切曲线方程为

y=ax

(8)

式中a——刃口曲线方程的底数

(9)

式中β——滑切曲线终止角，(°)

C——滑切曲线高度，mm

联立式(8)、(9)可得

(10)

综合可得铲柄曲线方程为

(11)

由式(11)可知，滑切曲线的形状由入土角δ、铲柄曲线终止角β和C来确定，铲柄曲线终止角β设计为80°，根据上文可知入土角δ为23°，结合玉米种植农艺要求，C确定为200 mm，因此a为1.33。

2.1.3材料选型

图6为仿真试验得到的深松铲前进阻力变化曲线，由此可知深松铲受到的平均阻力f1为5 073 N，受到的最大阻力fmax是6 250 N。

深松铲上部固定在机架上，工作时受弯矩作用，阻力臂L长0.56 m。

计算得深松铲受到的最大弯矩Ma为

Ma=fmaxL=3 500 N·m

(12)

深松铲截面为70 mm×25 mm的矩形，因此计算出截面的抗弯截面模量Wz为

(13)

式中b——横向截面长度，m

h——纵向截面长度，m

由式(12)、(13)可得屈服应力σ为

(14)

因此选用Q460作为该深松铲材料，其屈服强度为460 MPa，深松铲受到的屈服应力为171.6 MPa，远小于460 MPa。

2.2 施肥管结构设计

施肥管安装在深松铲的后方，且出肥口要与前进方向保持一定夹角，如图7所示。根据文献[10]对比影响施肥配比的因素可知，夹角为36°时，肥料分层效果较好。施肥管包含4个出肥口，上、中、下出肥口均安装有固定施肥板，玉米植株生长特性需要土层施肥量上少下多，因此施肥板长度不同[29]，各施肥口垂直方向上间隔5 cm，施肥深度分别为0～5 cm、5～10 cm、10～15 cm、15～20 cm。

3 EDEM仿真分析

通过EDEM软件对施肥过程进行模拟，对施肥的分层效果进行仿真分析，仿真中施肥板与水平面安装角为36°，研究发现安装角确定后，各施肥口的施肥量即确定。

3.1 仿真模型建立

EDEM中提供多种力学接触模型，研究肥料颗粒时，肥料与肥料颗粒之间采用的是Hertz-Mindlin(no-slip)接触力学模型，研究土壤时采用Hertz-Mindlin with bonding模型，根据文献[10]，确定模型相关参数如表1、2所示。

表1 土壤、肥料以及施肥铲参数Tab.1 Parameters of soil, fertilizer and shovel

表2 不同材料接触参数Tab.2 Contact parameters of different materials

肥料属于类球形颗粒，其球形率在90%以上，因此仿真模型可用球体代替肥料颗粒[11]，通过试验测量千粒肥料颗粒的直径均值为3 mm，且符合正态分布的规律，所以用直径3 mm的等效球体在EDEM中进行替代，并且利用EDEM软件中自动计算肥料的数据，质量0.026 3 g，体积1.41×10-8m3，施肥量750 kg/hm2。

按照表1、2的参数设定仿真模型，如图8所示。

图9为施肥管静态出肥量情况。仿真模型下方有4个收集器，便于利用EDEM软件的后处理模块对肥料进行统计与计算。

图10为5次静态排肥试验后得到的施肥量柱状图，5次试验后4层肥料占比均值依次为7%、18%、25%、50%。

3.2 仿真分析

通过EDEM的仿真分析，在控制单一变量的原则下，分别提取出了不同工作速度、不同作业深度下肥料纵面分布，如图11、12所示，不同的工作速度和作业深度导致肥料的横向扩散距离不同，工作速度和作业深度会影响肥料的均匀分布，因此本文将选取工作速度和作业深度2个因素研究各层肥量均匀性变异系数的变化规律。

3.3 不同土层肥量均匀性变异系数测量

在实际生产中，同一土层中肥量的均匀性会影响到作物生长，从而影响产量[30-32]，因此取肥量均匀性变异系数作为本试验的衡量指标，每层肥量取连续30段，每段长10 cm，分别计算每段肥料颗粒数目xi，每层肥量均匀性变异系数yj为

(15)

3.4 参数回归正交试验设计

结合正交试验的设计原理，选取工作速度x1和作业深度x2为试验因素，根据实际情况，工作速度为3～7 km/h，作业深度为21～29 cm，试验因素编码如表3所示。

表3 试验因素编码Tab.3 Horizontal coding of test factors

3.5 仿真试验结果

根据二次回归通用旋转组合设计并进行13组试验，按照试验方法分别进行试验，得到所需样本，借助EDEM的Grid Bin Group得到样本容量，计算出各组试验肥量均匀性变异系数。试验方案和结果如表4所示，表中X1、X2为编码值。

表4 试验方案及结果Tab.4 Test plan and results

通过对试验数据的处理，肥量均匀性变异系数方差分析结果如表5～8所示。

表5 0～5 cm土层肥量均匀性变异系数方差分析Tab.5 Variance analysis of variation coefficient of fertilizer uniformity in 0～5 cm soil layer

由表5～8拟合得到各因素影响肥量均匀性变异系数yi关于工作速度x1和作业深度x2的回归方程为

(16)

(17)

(18)

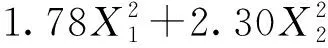
(19)

根据回归方程式(16)～(19)，利用Design-Expert软件绘制出工作速度与作业深度对肥量均匀性变异系数的响应曲面，如图13所示。根据响应曲面图13与表5～8可知，0～5 cm土层肥量均匀性变异系数较大，原因是由于工作中上方土壤回流滞后严重，肥料颗粒不能及时定位，因此变异系数较大；5～10 cm、10～15 cm、15～20 cm土层肥量均匀性变异系数变化趋势基本相同，但由上层到下层肥量均匀性变异系数依次减小，原因是同样受到土壤回流滞后的影响，随着深度增加，回流滞后的影响逐渐减小。通过方差分析可以看出，作业深度对肥量均匀性变异系数的影响比前进速度对肥量均匀性变异系数的影响小。当工作速度一定时，肥量均匀性变异系数随着入土深度增加而增大，当作业深度一定时，肥量均匀性变异系数随着工作速度的增加先增大后减小，在两者交互的情况下，肥量均匀性变异系数有明显的上升趋势。

表6 5～10 cm土层肥量均匀性变异系数方差分析Tab.6 Variance analysis of variation coefficient of fertilizer uniformity in 5～10 cm soil layer

表7 10～15 cm土层肥量均匀性变异系数方差分析Tab.7 Variance analysis of variation coefficient of fertilizer uniformity in 10～15 cm soil layer

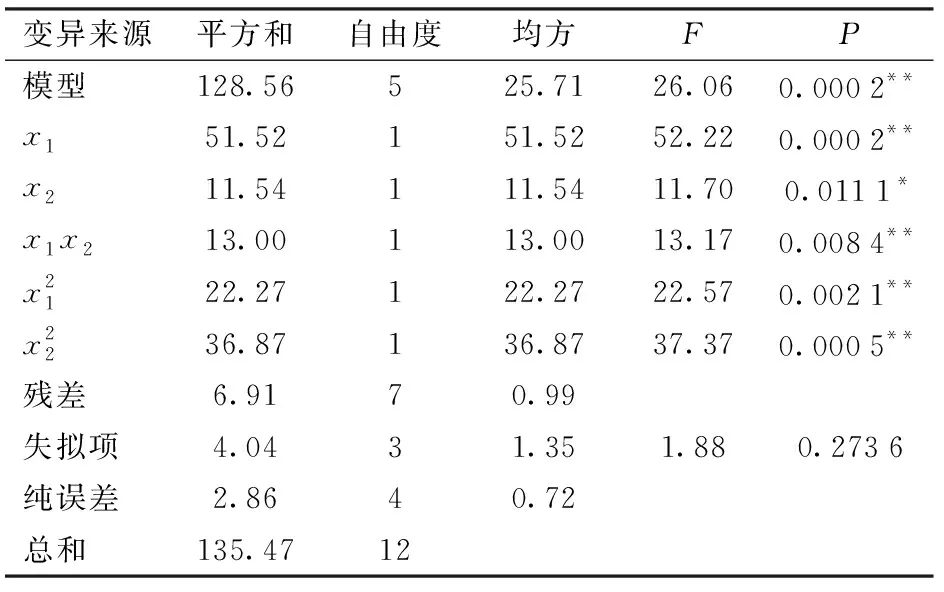
表8 15～20 cm土层肥量均匀性变异系数方差分析Tab.8 Variance analysis of variation coefficient of fertilizer uniformity in 15～20 cm soil layer

3.6 参数的优化求解

利用Design-Expert软件对响应面进行优化求解处理，得到最优的工作参数组合为：工作速度3.81 m/s，作业深度25.22 cm，0～5 cm、5～10 cm、10～15 cm和15～20 cm土层的肥量均匀性变异系数分别为37.02%、25.13%、19.84%、14.19%，符合JB/T 6274.1—2013《谷物播种机》的行业标准，设计可靠。

4 整机设计

该机具在播种开沟器前端安装了带状深松全层施肥装置，如图14所示。该装置在对播种带土壤深松的同时进行全层定点施肥，同时设置在该装置两侧的圆盘盘配合深松铲将苗带土壤进行整备，并经过后置的碎土机构碎土镇压，玉米精密播种单元在经过深松整备的清洁苗带上进行精密播种，从而实现带状深松全程施肥精密播种作业。

5 田间试验

为进一步验证此深松全层施肥铲离散元仿真试验的可靠性，开展田间试验进行验证。

结合仿真试验结果，重新设计制作试验部件，作业深度为25 cm，施肥位置0～20 cm，试验于2021年4月28日在吉林省扶余市试验地进行，以John Deere 3B-604型拖拉机为动力，待测部件搭载在带状免耕播种机上，如图15所示。前茬作物为玉米，常规免耕播种；玉米种植行距60 cm，株距26 cm，田间土壤平均含水率23%，秸秆覆盖率60%，玉米品种为能大115，化肥为保利复合肥(N 15%、P2O515%、K2O 15%)。

以最优参数(圆整为工作速度4 m/s，作业深度25 cm)进行试验。由于田间肥料分布难以采集，本试验采取作业完成后剖开土壤截面，记录各层的肥料颗粒数目，如图16所示。

试验计算得0～5 cm、5～10 cm、10～15 cm和15～20 cm土层的肥量均匀性变异系数分别为41.05%、24.11%、20.31%、14.63%，试验值与理论优化值相对误差分别为10.89%、4.06%、2.37%、3.10%。

6 结论

(1)为提高化肥利用率，以及适应作物不同生育期肥料需求，本文设计了一种玉米深松全层施肥铲，可将肥料按照上少下多的方式施入土壤中，且能够疏松深层土壤，为种子萌发提供良好的生长种床。

(2)通过二次回归通用旋转组合试验得出工作速度和作业深度与肥量均匀性变异系数的回归方程，响应面图分析表明，作业深度对变异系数的影响比工作速度对变异系数的影响小，在两者交互的作用下，肥量均匀性变异系数有明显的上升趋势。

(3)通过Design-Expert软件对响应面进行优化求解，田间试验表明，本设计在最优的工作参数组合工作速度4 m/s、作业深度25 cm下，具有最佳施肥性能，各层肥量均匀性变异系数分别为41.05%、24.11%、20.31%、14.63%。