基于LAI和VTCI及Copula函数的冬小麦单产估测

王鹏新 陈 弛 张树誉 张 悦 李红梅

(1.中国农业大学信息与电气工程学院， 北京 100083; 2.陕西省气象局， 西安 710014)

0 引言

冬小麦是我国主要粮食作物之一，对冬小麦进行大规模的长势监测和产量估测，不仅能为地方政府制定生产计划提供科学依据，也能为粮食安全提供保障。近年来，遥感技术以其快速、简便、宏观、无损及客观等优点被广泛应用于农业生产的各个环节[1]。国内外学者通常使用可以表征作物生长信息的植被指数(Vegetation index，VI)来建立与作物产量间的经验模型，进而进行作物估产。以往的研究中常用的植被指数有归一化植被指数(Normalized difference vegetation index，NDVI)[2]、增强型植被指数(Enhanced vegetation index，EVI)[3]、比值植被指数(Ratio vegetation index，RVI)[4]等。利用遥感技术获得的叶面积指数(Leaf area index，LAI)可以反映作物光合作用、呼吸作用、蒸腾作用及碳氮循环等生物物理过程[5]，常作为作物长势监测和产量估测的重要参数[6]。然而作物单产不仅与植被指数及其相关的长势参数有关，还与土壤水分有密切联系。在NDVI和地表温度(Land surface temperature，LST)的散点图呈三角形区域分布的基础上，文献[7]提出条件植被温度指数(Vegetation temperature condition index，VTCI)的干旱监测方法，弥补了单一遥感干旱监测指数的不足，并在干旱监测、预测和影响评估等领域得到了广泛的应用。在此基础上，综合考虑作物长势与干旱胁迫可以更加准确地描述作物生长状态，从而提高作物产量估测精度。

Copula函数是构造多元联合分布和随机变量间相关结构的重要工具。近年来，Copula函数以其在多变量分析中的便利性引起了学者们的广泛关注，它能够将变量的相关性结构与边缘分布分开处理，考虑变量间的非线性与非正态关系，没有任何限制[8-10]。VERGNI等[11]将Copula理论应用于农业干旱领域，利用Student Copula获得了向日葵相对发病率和相对严重程度的联合概率以及双变量返回期，为干旱规划和管理提供了有用的信息。张迎等[12]综合降雨和径流两种要素，基于Archimedean Copula构建了一种能够综合表征气象干旱和水文干旱的新型综合干旱指标，并用其表征渭河流域的干旱演变特征。针对Copula函数构建多元随机变量间联合分布时参数求解困难、不同Copula函数的参数不尽相同的问题，王鹏新等[13-14]分别利用主成分分析法(Principal component analysis，PCA)和核主成分分析法(Kernel PCA，KPCA)提取VTCI的主成分因子，基于Copula函数评估冬小麦主要生育期干旱对其产量的影响，验证了Copula函数对基于VTCI的干旱影响评估研究具有较好的适用性。然而作物的长势和产量是多个指标共同作用的结果，仅靠单一的指标进行作物长势监测研究难以反映不同指标在作物生长与产量估测过程中的相互影响[15]。因此，本文以陕西省关中平原为研究区域，选取VTCI和LAI为长势监测指标，将PCA应用于提取单个、两个特征变量的主成分数据，再结合无需求解参数的乘积Copula函数构建综合长势监测指标，并建立综合长势监测指标与冬小麦单产之间的线性回归模型，以期获得更准确的冬小麦单产估测方法。

1 材料与方法

1.1 研究区域概况

关中平原位于陕西省中部的渭河流域，西起宝鸡大散关，东至渭南潼关，北到陕北黄土高原，南至秦岭，坐标为106°22′～110°24′E，33°57′～35°39′N。行政区域包括西安市、铜川市、宝鸡市、咸阳市、渭南市和杨凌国家农业高新技术产业示范区，其中杨凌国家农业高新技术产业示范区由于面积较小，故将其划分到咸阳市境内。关中平原是陕西省的农业基地，也是全国粮食主要生产基地之一[16]。该区域年平均气温在6～13℃之间，年平均降雨量在550～700 mm之间，但分布极不均匀，11月到次年5月易发生干旱[17]。受全球气候变暖影响，农业干旱灾害不断加剧，由干旱造成的冬小麦减产现象时有发生[18-19]。

1.2 试验数据

1.2.1时间序列VTCI的生成

选取关中平原2012—2017年每年3—5月的Aqua-MODIS遥感数据的日地表反射率产品(MYD09GA)和日地表温度产品(MYD11A1)，获取日LST和日NDVI，通过最大值合成法分别逐像素取10 d内所包含的多日LST和NDVI的最大值作为该像素的LST和NDVI值，即获得旬LST和旬NDVI最大值合成产品。将多年某一旬的LST和NDVI最大值合成产品再一次运用最大值合成技术，生成多年旬尺度LST和NDVI最大值合成产品。基于最小值合成技术将多年某一旬LST的最大值合成产品逐像素取最小值，得到多年旬尺度LST最大-最小值合成产品；通过多年旬尺度NDVI和LST最大值合成产品确定研究区域VTCI的热边界，通过多年旬尺度NDVI最大值合成产品和多年旬尺度LST最大-最小值合成产品确定VTCI的冷边界。VTCI计算公式为[20-21]

(1)

其中

LSTmax(NDVIi)=a+bNDVIi

(2)

LSTmin(NDVIi)=a′+b′NDVIi

(3)

式中LST(NDVIi)——研究区域内某一像素的NDVI值为NDVIi时的地表温度

LSTmax(NDVIi)——研究区域内当NDVI值等于NDVIi时的所有像素地表温度的最大值，称作热边界

LSTmin(NDVIi)——研究区域内当NDVI值等于NDVIi时的所有像素地表温度的最小值，称作冷边界

a、b、a′、b′——待定系数，由研究区域NDVI和LST的散点图近似获得

VTCI的取值范围为[0,1]，其中，VTCI值越小，表示旱情越严重，值越大，则相反。根据越冬后冬小麦的生长情况，将越冬后的生育时期划分为返青期(3月上旬—中旬)、拔节期(3月下旬—4月中旬)、抽穗-灌浆期(4月下旬—5月上旬)和乳熟期(5月中旬—下旬)4个生育时期[22-23]。取某一生育时期内多旬VTCI的平均值作为该生育时期的VTCI值，叠加关中平原的行政矢量图，取各县(区)所包含像素的VTCI的平均值作为该地区该生育时期的VTCI值。

1.2.2时间序列LAI的生成

选取2012—2017年冬小麦主要生育时期的MCD15A3H产品，与MOD15A2(Terra-MODIS)和MYD15A2(Aqua-MODIS)产品相比，MCD15A3H具有较高的时间分辨率(4 d)和空间分辨率(500 m)，对于监测农作物的生长和物候特性更为有利。原始叶面积指数产品由于云和大气等因素的影响，会导致LAI数据出现骤降现象，从而降低准确性。为了解决这个问题，应用上包络线Savitzky-Golay(S-G)滤波对原始时间序列LAI进行平滑处理[24]，经上包络线S-G滤波平滑处理后的叶面积指数数据更加符合冬小麦的生长情况。

为了使LAI和VTCI具有相同的取值范围，将S-G滤波后的LAI进行归一化处理；逐像素取所在旬LAI的最大值作为该旬的LAI，取各生育时期所包含的多旬LAI的平均值作为该生育时期的LAI值，通过叠加研究区域的行政矢量图，取各县(区)所包含像素的LAI的平均值作为该地区该生育时期的LAI值。

1.2.3冬小麦单产数据来源

《陕西统计年鉴》记录了冬小麦的产量数据。因此，关中平原各县(区)2012—2017年的单产数据均来源于其所在市(西安市、咸阳市、宝鸡市、渭南市)的统计年鉴。

1.3 PCA-Copula法

主成分分析是一种多元统计方法，可通过降维技术将多个变量转换为少数几个主成分，这些主成分能够反映原始变量的大部分信息，通常表示为原始变量的线性组合。由于主成分因子是新的互相独立的变量，因此在建立Copula函数时无需求解参数，计算简便。

1.3.1主成分分析

首先根据样本数据构建矩阵An×p，计算协方差矩阵Rp×p，进而求出矩阵的特征值λi(i=1, 2,…,p)及其对应的单位特征向量ei，各主成分的贡献率Di用来反映其信息量[13]，计算公式为

(4)

最终选择几个主成分，即PC1,PC1,…,PCm中的m通常由主成分的累计贡献率G(m)来确定，计算式为

(5)

根据经验，当G(m)大于85%时，认为能足够反映原来的信息，对应的m就是选取的前m个主成分。第r个主成分的线性表示为

PCr=a1rX1+a2rX2+…+aprXp
(r=1,2,…,m)

(6)

式中PCr——第r个主成分因子

apr——所选指标在第r个主成分线性组合中的系数

p——原变量所选指标的个数

Xp——所选指标(如VTCI、LAI)的值

1.3.2Copula函数

Copula函数是定义在[0, 1]上均匀分布的随机向量的联合分布函数。根据Sklar定理[25]，联合分布函数与相关结构函数之间存在一一对应的关系，Copula函数形式可表示为

F(x1,x2,…,xj)=Cθ(F1(x1),F2(x2),…,Fj(xj))=
C(u1,u2,…,uj)

(7)

其中

uj=F(xj)

式中F——随机变量分布函数

j——样本容量

C——Copula函数

uj——随机变量xj的最优边缘分布函数

由于采用PCA方法提取样本数据的m个主成分因子间互无相关性，故可以通过相应的乘积Copula获取综合长势监测指标，即

(8)

式中I——基于前m个主成分确定的综合长势监测指标

1.3.3边缘分布函数确定与优度评价

由给定样本集合求解随机变量边缘分布函数的方法包括参数法和非参数法。其中参数法是假定总体服从某种已知的分布，利用极大似然法估计分布函数的参数，这种方法依赖于实现对总体分布的假设。常用的分布线型包括皮尔逊Ⅲ型分布、正态分布、广义极值分布、对数分布、指数分布等[26]。首先通过Kolmogorov-Smirnov(K-S)方法检验样本是否服从指定的分布，原假设为样本服从指定分布，备择假设为不服从指定分布。当输出检验值h=1时，在显著性水平下拒绝原假设；h=0时，则在显著性水平下接受原假设。若该样本某一主成分的多个指定分布均通过K-S检验，则通过各边缘分布的理论频率与经验频率之间的均方根误差(Root mean square error，RMSE)及赤池信息准则值(Akaike information criterion，AIC)评估拟合效果，RMSE和AIC越小，表明拟合效果越好[27]。一维随机分布的经验频率[28]计算公式为

(9)

式中N——样本数

s——从最小样本开始观察的顺序值

Qs——第s项的累计经验频率RMSE计算公式为

(10)

式中Qsir——第r个主成分第i个数据的经验频率

Qtir——第r个主成分第i个数据的理论频率

n——第r个主成分因子中数据的个数，取n为144

AIC计算公式为

VAIC=nlnVRMSE+2σ

(11)

式中σ——所选模型中参数的个数

当样本总体分布未知或不符合常见分布的线型时，则不易用参数法对边缘分布作出估计。非参数法则避开了线型选择的问题，经验分布与核密度估计均属于非参数检验方法，它们可以从样本数据本身出发研究数据分布的特征，估计未知的分布函数，不受限于事先对总体分布做出假设。

2 结果与分析

2.1 冬小麦4个生育时期各长势监测指标的主成分分析

由于VTCI和经归一化处理后的LAI的取值范围均为[0,1]，因此直接通过PCA方法对原始数据进行降维处理，根据主成分相应累计贡献率达到85%以上的原则选取主成分(表1)。VTCI第1主成分的贡献率为64.78%，第2主成分贡献率为25.61%，前2个主成分的累计贡献率为90.39%；LAI的第1主成分贡献率达到91.68%，第2主成分贡献率为7.10%，前2个主成分的累计贡献率为98.78%；VTCI和LAI双变量数据、共8项指标经PCA处理后的前3个主成分的贡献率分别为59.44%、14.41%和12.27%，其累计贡献率为86.12%。

表1 冬小麦4个生育时期不同长势监测指标的主成分贡献率及其线性表达式Tab.1 Principal component contribution rates and linear expressions of different growth monitoring indices at four growth stages of winter wheat

2.2 主成分因子边缘分布函数的确定

基于目前常用的分布线型，选取正态分布、广义极值分布和对数分布分别拟合冬小麦4个生育时期各长势监测指标的主成分因子，应用极大似然法获得对应的边缘分布函数参数，利用K-S检验对各主成分的边缘分布函数进行拟合优度评价(表2)。可以看出，各长势监测指标主成分因子的分布拟合情况分为2种，指定的3种分布均未通过K-S检验与仅通过正态分布和广义极值分布的K-S检验。以VTCI的第1、2主成分为例，阐述边缘分布函数的选择过程。VTCI第1主成分的正态分布、广义极值分布和对数分布均未通过K-S检验，因此选用非参数法拟合该主成分的边缘分布。由图1可见，VTCI第1主成分因子经验分布和核分布估计曲线的走势基本吻合，因此优选更加光滑的核分布估计结果作为该主成分的边缘分布。VTCI第2主成分的正态分布和广义极值分布均能通过K-S检验，依据边缘分布的理论频率与经验频率之间RMSE及AIC确定最优边缘分布(式(9))。经计算，广义极值分布的拟合结果(VRMSE=0.013，VAIC=-616.592)优于正态分布的拟合结果(VRMSE=0.016，VAIC=-592.383)，因此VTCI的第2主成分优选广义极值分布。同理可以得出，LAI的第1主成分优选广义极值分布，第2主成分选择核分布；VTCI和LAI的第1、2、3主成分均优选广义极值分布(表2)。

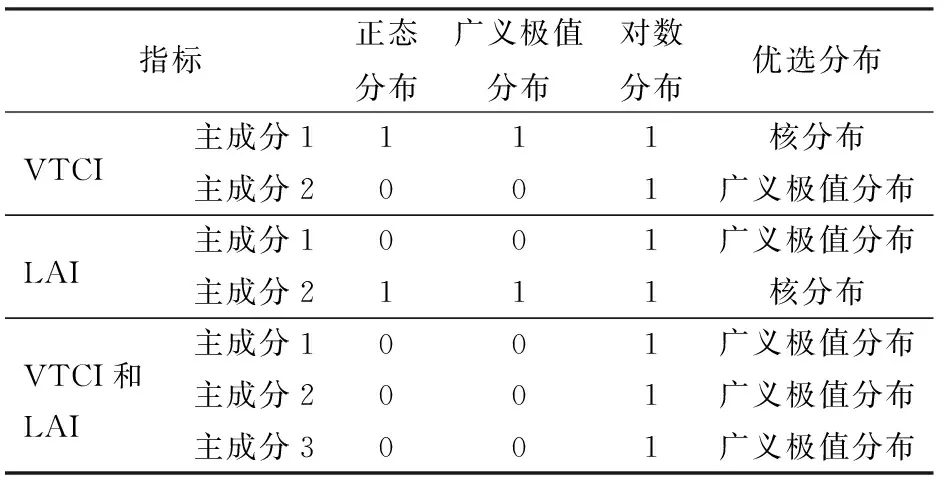
表2 冬小麦4个生育时期不同长势监测指标主成分因子的K-S检验值(h)及其优选分布Tab.2 K-S test value (h) and optimal distribution of principal components of different growth monitoring indices at four growth stages of winter wheat

2.3 综合长势监测指标与冬小麦单产间的线性回归分析

以VTCI为例，阐述综合长势监测指标的构建过程。从表1中VTCI第1主成分PCV1的表达式看，返青期VTCI的系数最大，其他生育时期的系数比较小，说明返青期VTCI对PCV1的影响最大。从第2主成分PCV2的表达式看，V1的系数为负数，说明随着返青期VTCI的减小，PCV2增大，可能是由于返青期的干旱的补偿效应造成的，即在冬小麦返青期发生一定程度的水分胁迫不会对作物生长造成太大的影响，反而能够提高作物在生育后期的水分利用效率，使产量增加[29]；PCV2在拔节期VTCI、抽穗-灌浆期VTCI、乳熟期VTCI上有均相近的正系数，说明这3个生育时期对PCV2的重要性都相似。基于此，分别以各主成分的贡献率在其累计贡献率中所占的比重将主成分综合，进一步获取前2个主成分的综合线性表达式为

PCV=0.717PCV1+0.283PCV2

(12)

将VTCI前2个主成分的线性表达式(表1)代入式(12)得到综合评价值为

PCV=0.664V1+0.246V2+0.218V3+0.213V4

(13)

由式(13)可见，返青期VTCI的系数最大，乳熟期VTCI的系数最小。但拔节期是干旱对冬小麦生长影响的关键因素，其次为抽穗-灌浆期，返青期和乳熟期的影响相对较小[22-23]。该模型的构建没有考虑前2个主成分各自的分布特征，因此仅采用主成分分析得到的综合评价值PCV存在不足，而将主成分分析与Copula函数结合的方法不受各个单因子变量边缘分布的影响。因此，根据各主成分对应的最优边缘分布特征建立联合分布(式(8))，进而构建不同的综合长势监测指标。

由于表1中选择各长势监测指标的主成分个数均基于经验方法，没有理论支持该方法反映出的信息量最优，因此利用PCA-Copula方法计算基于VTCI和LAI的包含不同主成分个数的综合长势监测指标，进而与冬小麦单产进行线性回归分析(图2、3、4)。结果表明，综合VTCI包含第1个主成分时(记为综合VTCI-1)与冬小麦单产的相关性较低(R2=0.066，P=0.002)(图2)；综合VTCI包含前2个主成分(记为综合VTCI-2)与冬小麦的相关性达到极显著水平(R2=0.246，P<0.001)，此时综合VTCI-2中包含的主成分也符合主成分个数的选取原则。

综合LAI包含第1个主成分(记为综合LAI-1)与冬小麦单产的相关性(R2=0.567，P<0.001)优于综合LAI包含前2个主成分(记为综合LAI-2)与冬小麦单产的相关性(R2=0.234，P<0.001)(图3)。这是由于建立LAI的第2主成分PCL2表达式(表1)中抽穗-灌浆期LAI、乳熟期LAI系数均为负值，即PCL2在抽穗-灌浆期LAI、乳熟期LAI均有中等程度的负载荷。LAI与作物的长势及产量呈正相关，因此表达式中负系数与实际情况不符，加入后会带来噪声，使精度下降。分析表明，利用PCA-Copula方法进行作物长势监测和产量估测时，主成分的选取并非越多越好，不仅需分析所采用方法的理论基础，而且需分析建立的各主成分表达式中各长势监测指标的系数与作物长势间的关系。

综合VTCI和LAI包含第1个主成分(记为综合G-1)与冬小麦单产之间的回归结果(R2=0.524，P<0.001)优于综合VTCI和LAI包含前2个主成分(记为综合G-2)与冬小麦单产之间的回归结果(R2=0.263，P<0.001)，以及综合VTCI和LAI包含前3个主成分(记为综合G-3)与冬小麦单产之间的回归结果(R2=0.117，P<0.001)(图4)。随着第2、3主成分的加入，综合VTCI和LAI与冬小麦单产之间的相关性逐渐降低。这是由于建立VTCI和LAI的第2主成分PCVL2表达式(表1)中拔节期VTCI、抽穗-灌浆期VTCI、乳熟期VTCI系数均为负值，其中PCVL2在乳熟期VTCI有中等程度的负载荷；建立VTCI和LAI的第3主成分PCVL3表达式(表1)中的4个负系数均与LAI相关。VTCI已被证明能够准确地反映作物水分胁迫信息，LAI与作物的长势和产量密切相关，PCVL2、PCVL3表达式中负系数指标的加入会导致综合值变小，精度下降，不符合实际情况。

由此可见，尽管没有满足主成分的累计贡献率不低于85%的要求，但包含综合长势监测指标第1个主成分的综合LAI-1、综合G-1相比于综合VTCI-2与冬小麦产量之间的关系更为紧密，以PCA-Copula方法为基础计算作物综合长势监测指标时，仅仅考虑主成分分析的理论基础不够全面，更需考虑各长势监测指标对作物长势监测结果产生的实际影响，从而建立与作物长势和产量最密切的综合长势监测指标。

2.4 冬小麦单产估测的精度评价

基于包含最优主成分个数的各综合长势监测指标分别建立估产模型，计算关中平原24个县(区)的估测单产。利用综合VTCI-2建立的冬小麦估产模型估测单产与实际单产的均方根误差为733.64 kg/hm2，相对误差为0.05%～57.76%，平均相对误差为13.99%；利用LAI-1建立的冬小麦估产模型估测单产与实际单产的均方根误差为556.28 kg/hm2，相对误差为0.18%～73.21%，平均相对误差为10.31%；利用综合G-1建立的冬小麦估产模型估测单产与实际单产的均方根误差为582.81 kg/hm2，相对误差为0.03%～54.79%，平均相对误差为11.03%。相比之下，基于综合VTCI-2建立的估产模型精度较低；基于综合LAI-1和综合G-1建立的估产模型总体估产误差较小，其中综合LAI-1建立的估产模型计算的估测单产存在部分年份或部分地区的冬小麦估测结果与实际偏差较大的情况。

为了进一步验证估测模型的精度，将基于综合LAI-1、综合G-1建立的冬小麦估产模型分别用于分析2012—2017年关中平原24个县(区)估测单产与实际单产的均方根误差和平均相对误差(表3)。基于综合LAI-1构建的冬小麦单产回归模型各县(区)估测单产与实际单产均方根误差为126.74(三原县)～1 148.87 kg/hm2(眉县)，估测单产与实际单产的平均相对误差以三原县最低，为2.35%，以蒲城县最高，为26.40%。基于综合G-1构建冬小麦单产回归模型各县(区)估测单产与实际单产均方根误差为125.91(大荔县)～1 061.63 kg/hm2(阎良区)，估测单产与实际单产的平均相对误差以大荔县最低，为2.56%，以合阳县最高，为23.62%。上述结果表明，基于综合LAI-1建立估产模型的决定系数(R2)虽略高于基于综合G-1建立的估产模型，但具体到各县(区)的估产时，误差范围大于综合G-1所建立的估产模型，说明利用单一LAI构建的综合LAI得到的冬小麦估产结果容易存在偏差。相对于单一指标构建的综合VTCI或综合LAI，基于双变量构建的综合干旱指标(综合VTCI和LAI)得到的冬小麦估产结果更加全面可靠，可用于研究区域冬小麦单产的估测。

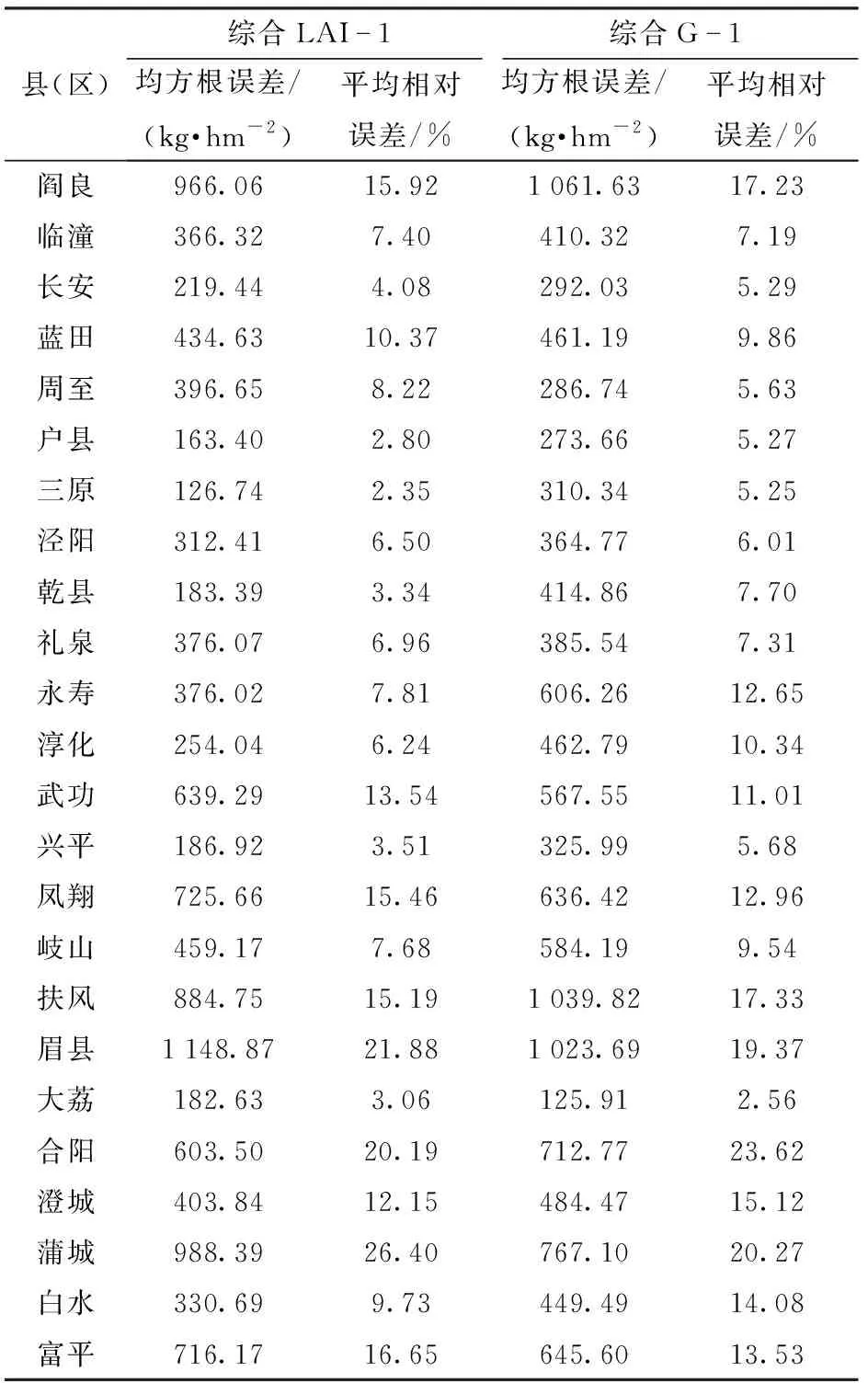
表3 关中平原各县(区)2012—2017年冬小麦估测单产与实际单产对比Tab.3 Comparison of estimated and actual winter wheat yields for each county (district) in Guanzhong Plain from 2012 to 2017

3 讨论

已有研究表明Copula函数对于基于VTCI的干旱影响评估具有良好的适用性[13-14]，LAI可以反映作物在不同时间阶段生长发育的动态特征和健康状况，是表征作物长势与进行产量预报的重要参数。鉴于此，本文基于冬小麦越冬后主要生育期VTCI、LAI为长势监测指标，尝试利用PCA-Copula法分别建立冬小麦主要生育期单变量(综合VTCI或综合LAI)、双变量(综合VTCI和LAI)的估产模型。由主成分分析提取出的少数的几个主成分因子几乎保留了原始变量的全部信息，在大多实际研究工作中，选取主成分的个数有多种方法，常使用的原则是主成分的特征值大于1或累计贡献率大于85%。它的优势在于计算简单，且对多数情况适用。但此方法没有理论支持，属于经验性方法。基于此，本文首先根据主成分的累计贡献率不小于85%的选取原则，在此基础上尝试令结合Copula获得的综合长势监测指标包含不同的主成分个数，对比它们与冬小麦单产之间的拟合效果。

综合LAI、综合VTCI和LAI均包含第1个主成分时与单产间的拟合效果更好，这是由于LAI的第2个主成分表达式、VTCI和LAI的后2个主成分表达式中存在载荷量较大的负系数。VTCI和LAI均与冬小麦的长势与产量密切相关，两者的值越大，作物长势越好、产量超高，因此负系数的出现不符合实际情况，加入后易导致精度降低。这一规律表明，开展多指标的主成分分析时，不仅要考虑主成分的累计贡献率，而且更要考虑各指标的系数与作物长势间的关系。

利用综合LAI构建的估产模型虽然模型的拟合精度较高，但只考虑单一指标对冬小麦产量进行估测结果存在偏差。具体到每一个县时，利用双变量指标综合G-1构建的冬小麦单产模型得到的估测单产误差范围比基于单变量构建的模型更集中，结果更加可靠。研究成果表明，使用BP神经网络和IPSO-BP神经网络构建双变量(VTCI和LAI)冬小麦估产模型的R2分别为0.310、0.342[30]。相比之下，利用综合G-1构建估产模型的R2更高，进一步说明基于PCA-Copula方法构建的双变量估产模型精度较高，可用于研究区域冬小麦单产估测。

4 结论

(1)采用PCA-Copula法分别对关中平原2012—2017年24个县(区)冬小麦主要生育时期单变量(VTCI或LAI)、双变量(VTCI和LAI)进行处理，获得综合VTCI、综合LAI、综合VTCI和LAI。结果表明，综合VTCI包含前2个主成分时与冬小麦单产的拟合精度优于包含第1个主成分的情况；综合LAI包含第1个主成分时与单产的拟合精度高于综合LAI包含前2个主成分；综合VTCI和LAI包含第1个主成分时比包含前2个、3个主成分时与单产间的拟合效果好。

(2)综合LAI-1与冬小麦单产间的回归模型拟合效果最好(R2=0.567，P<0.001)，综合G-1与冬小麦单产间的回归模型略次之(R2=0.524，P<0.001)，综合VTCI-2构建的估产模型拟合效果相对较差(R2=0.246，P<0.001)。具体到各县(区)的单产估测时，尽管综合LAI-1与单产间的相关性高于综合G-1与单产间的相关性，但基于综合LAI-1的估测单产相比于基于综合G-1的估测单产与实际单产之间的误差范围更大，说明基于单一LAI构建的综合长势监测指标反映的冬小麦长势与产量信息不够全面。因此，基于双变量综合VTCI和LAI构建的冬小麦估产模型更加全面可靠。