基于RSM和GA-BP-GA优化的油茶籽仿真参数标定
丁辛亭 李 凯 郝 伟 杨其长 闫锋欣 崔永杰
(1.西北农林科技大学机械与电子工程学院,陕西杨凌 712100;2.农业农村部农业物联网重点实验室,陕西杨凌 712100;3.中国农业科学院都市农业研究所,成都 610213)
0 引言
油茶(CamelliaoleiferaAbel.)作为中国特有的一种纯天然高级油料,广泛种植于浙江、江西、河南、湖南、广西等地区,种植面积超过4.47×106hm2,油茶籽、茶油产量分别达到3.14×106、7.2×105t[1]。通过推广优良品种、扩大种植面积、改造中低产林,油茶生产潜力持续提升,但是油茶籽剥壳、播种、栽植等生产加工环节的机械化水平仍然较低,成为制约油茶进一步发展的重要因素。
随着计算机技术的发展,离散元仿真为颗粒动态行为的虚拟仿真提供了一种全新的思路[2-3],具有省时省力、成本低、结果可视化等优点,为机具设计及优化提供理论依据[4]。国内外学者对土壤[5]、谷物[6-11]、三七[12]、花生[13]、葵花籽[14]等物料进行了离散元建模与参数标定,结果表明不同物料间的接触参数差异较大,而对油茶籽离散元仿真参数的标定鲜有报道。
以上各物料均采用响应面法(Response surface methodology,RSM)对显著性参数进行优化,而机器学习作为一种新兴的非线性回归建模方法,在数据拟合、预测和优化方面表现出优异的灵活性和预测能力。尤其是基于遗传算法(Genetic algorithm,GA)的BP(Back propagation)神经网络(GA-BP),能够避免RSM容易产生局部最优解的影响,更适合于达到全局最优组合设计的目标,具有更高的拟合度与精准的预测值[15],但该方法未见应用于离散元仿真参数优化与标定中。
本文以油茶籽为研究对象,采用逆向工程技术提取4种常见形状油茶籽的轮廓,在EDEM软件中建立填充球形颗粒的油茶籽离散元模型;结合油茶籽堆积角(Angle of repose, AOR)物理试验与仿真试验,通过Plackett-Burman Design和最陡爬坡试验筛选出对油茶籽堆积角有显著影响的参数及其取值范围;比较随机森林、支持向量机(Support vector regression,SVR)、BP人工神经网络(BP)和GA-BP 4种机器学习回归模型的预测能力和拟合稳定性,选择最优模型作为油茶籽堆积角预测模型;并与RSM方法对比,寻求最优的显著性参数组合,以进一步减小仿真误差、提高参数标定精度。
1 仿真参数标定方法
1.1 试验材料
本文油茶籽为2021年野生油茶籽,产自浙江省衢州市开化县。用数显游标卡尺(精度0.01 mm)随机测量100个油茶籽颗粒,其形状主要有球体、半球体、1/4球体和1/6球体,其各形状占比约为10%、30%、50%和10%。油茶籽半径分布如图1所示。
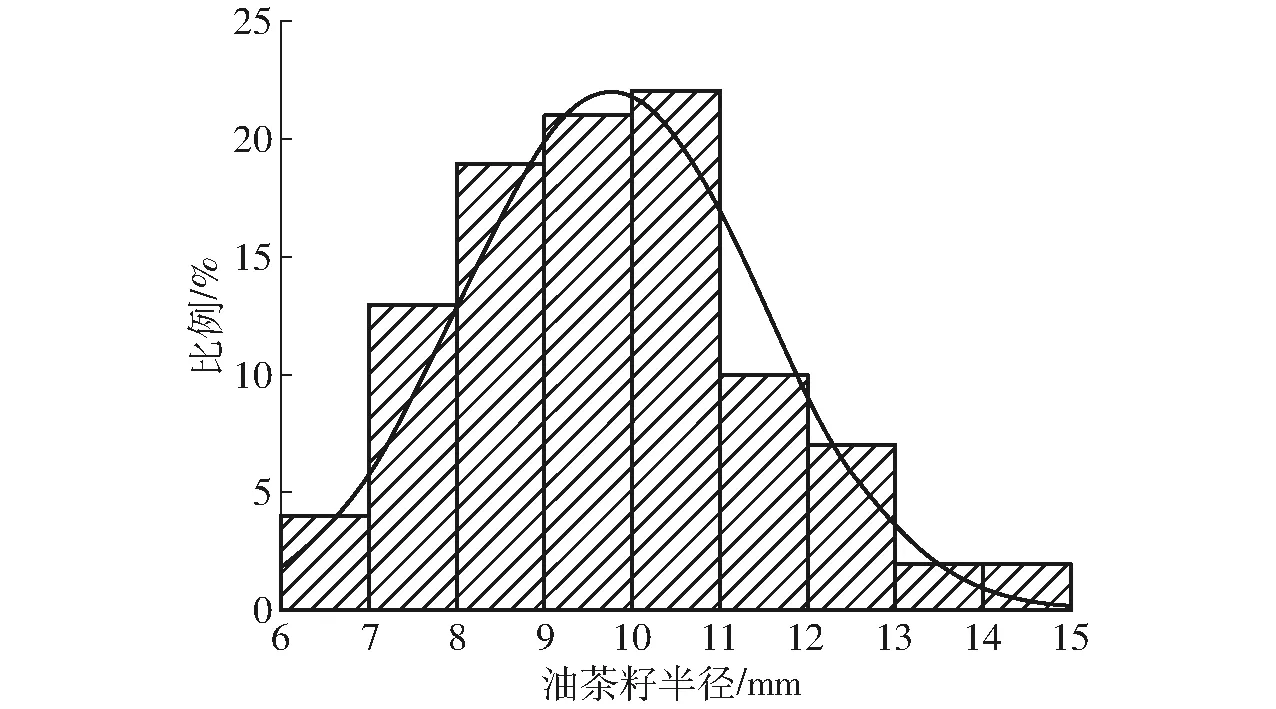
图1 粒径分布
使用排水法测量油茶籽密度。将质量为w的油茶籽缓缓放入100 mL量筒内,为了防止加水后油茶籽漂浮,将100 g砝码缓缓放入量筒内置于油茶籽上方。向量筒内添加50 mL水,测得总体积为v。使用同样方法测得100 g砝码体积为vF,油茶籽密度计算式为
(1)
通过5次试验测得油茶籽密度为0.864~0.996 g/cm3。
1.2 物理试验
1.2.1堆积角
将152.2 g油茶籽放入直径63 mm、高150 mm的无底316钢制圆筒中,圆筒以速度30 mm/s匀速上提,形成油茶籽堆。使用量角器测量堆积角误差较大,因此采用图像处理方法进行测量。使用基于Python语言的OpenCV 3.4开源软件包对颗粒堆进行图像处理,首先去除图像的冗余背景,得到原始图像(图2a),然后对原始图像进行灰度处理(图2b)和二值化处理(图2c),接着采用Canny边缘检测算法提取边界轮廓(图2d)并保存。最后采用Origin 2019b软件的Digitizer工具导入处理后的颗粒堆边界轮廓图像,设置图像像素与坐标轴后选取图像轮廓,即可得到轮廓像素点坐标(图2e),采用非线性拟合得到其高斯分布函数。参照文献[16-17]的高斯函数推导过程,得到油茶籽颗粒堆积角,该试验重复10次取平均值,最终得到油茶籽实际堆积角为(27.93±1.46)°。油茶籽仿真试验堆积角测量与该方法相同,且以堆积角物理试验平均值27.93°为参数标定的寻优目标。

图2 油茶籽堆积角图像处理
1.2.2碰撞恢复系数
(1)油茶籽-油茶籽间碰撞恢复系数
采用双摆装置(图3)测量油茶籽-油茶籽间碰撞恢复系数。油茶籽1与油茶籽2的外壳钻1 mm孔,并用相同长度的轻质尼龙绳连接油茶籽与钢杆。测试时,使用i-SPEED型高速摄影机(最高帧速率10 000 f/s)记录两油茶籽的运动轨迹。油茶籽1自然悬挂于最低点,油茶籽2与油茶籽1的相对高度(h0)为80 mm,油茶籽1以初速度为0释放,下落至最低点时与油茶籽2相撞,油茶籽1与油茶籽2继续摆动,其摆动最高点与最低点的垂直距离分别为h1和h2。根据碰撞恢复系数定义,油茶籽-油茶籽间碰撞恢复系数计算式为

图3 油茶籽-油茶籽间碰撞恢复系数测量
(2)
式中e1——油茶籽-油茶籽间碰撞恢复系数
v′1、v″1——碰撞前、后油茶籽1瞬时速度,m/s
v2——碰撞后油茶籽2瞬时速度,m/s
g——重力加速度,m/s2
由20次重复试验测试得到油茶籽-油茶籽间碰撞恢复系数为0.27~0.51。
(2)油茶籽-钢板间碰撞恢复系数
采用油茶籽自由落体碰撞钢板的方法(图4)测量油茶籽-钢板间碰撞恢复系数。测试时,使用高速摄影机记录油茶籽的运动轨迹。油茶籽在距钢板H0=170 mm以初速度为0释放,以自由落体状态与钢板相撞后反弹高度H1。根据碰撞恢复系数的定义,油茶籽-钢板碰撞恢复系数计算式为

图4 油茶籽-钢板间碰撞恢复系数测量
(3)
式中e2——油茶籽-钢板间碰撞恢复系数
v0、v1——碰撞前、后油茶籽速度,m/s
由20次重复试验测试得到油茶籽-钢板间碰撞恢复系数为0.33~0.53。
1.2.3油茶籽-钢板间静摩擦因数
使用斜面法测量油茶籽-钢板间静摩擦因数,试验装置如图5所示。选用非球形油茶籽置于可调坡度的斜面上,缓慢转动旋转轮使斜面一侧抬升,当油茶籽在斜面上具有下滑趋势时,记录油茶籽抬升高度a和此时油茶籽距离转轴距离b。油茶籽-钢板间静摩擦因数计算式为
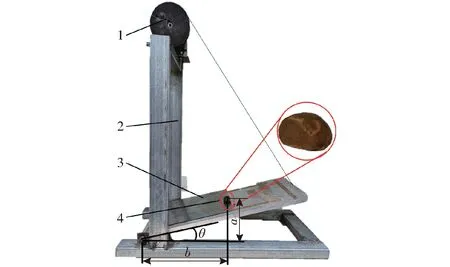
图5 油茶籽-钢板间静摩擦因数测量装置
(4)
式中f——油茶籽-钢板间静摩擦因数
θ——斜面与水平面的夹角,(°)
通过20次试验测得油茶籽-钢板间静摩擦因数为0.273~0.390。
1.3 仿真模型设置
离散元模型需要与实际物体外观大致相符合。在离散元仿真参数设置中,输入值不同时,得到的结果也不同。因此,以物理试验值的堆积角为目标,采用EDEM 2021软件对各个本征参数和接触参数进行寻优标定。
1.3.1油茶籽离散元模型建立
油茶籽为不规则形状颗粒,为了精确建立轮廓模型,选取半径与平均值相近的油茶籽建立轮廓模型,油茶籽实物如图6所示。应用逆向工程技术,通过OKIO 5M工业级三维扫描仪(5×106像素,测量精度5 μm,蓝光光栅扫描)扫描油茶籽外轮廓,将点云数据导至Geomagic Warp软件中进行合并拼接得到油茶籽模型,最后将油茶籽模型导入GOM Inspect软件,对尖锐、噪点进行锐化去噪得到油茶籽三维模型[12,14,18]。然后将油茶籽三维模型导入EDEM软件中进行颗粒自动填充,设置平滑值为5,最小颗粒半径为1.3 mm,得到由不等径颗粒组成的油茶籽离散元模型,球体、半球体、1/4球体、1/6球体颗粒数分别为5、40、40、37。

图6 油茶籽离散元模型构建过程
1.3.2钢板和无底钢制圆筒模型
用SolidWorks软件建立与试验装置相同的钢板和无底钢制圆筒的三维模型,将其保存为STP文件导入EDEM软件;参照文献[19]得到钢材泊松比为0.3,密度为7.865 g/cm3,剪切模量为79 700 MPa。
1.3.3接触模型
试验过程中,除颗粒与颗粒间接触,还会有颗粒与钢材之间的作用力。由于实际试验中油茶籽与钢材表面光滑且几乎无粘附力,因此仿真时选用Hertz-Mindlin(no slip)接触模型。
1.3.4仿真参数设置
在仿真试验时,以速率40粒/s、油茶籽形状按照1.1节所述比例生成100个油茶籽,仿真试验的Rayleigh时间步长约为20%,仿真总时长为7 s,数据保存时间间隔为0.1 s,网格尺寸为2.5倍的最小颗粒半径。
1.4 试验设计与方法
1.4.1RSM试验
(1)PBD试验
并不是所有参数都对堆积角有显著影响,没有显著影响的参数并不能基于堆积角来标定,否则标定的参数不准确[20]。利用Design-Expert软件进行PBD试验设计与分析,对油茶籽颗粒的本征参数(泊松比、剪切模量、密度)和接触参数(油茶籽-油茶籽间碰撞恢复系数、油茶籽-钢板间碰撞恢复系数、油茶籽-油茶籽间静摩擦因数、油茶籽-钢板间静摩擦因数、油茶籽-油茶籽间滚动摩擦因数和油茶籽-钢板间滚动摩擦因数)进行筛选,筛选出对油茶籽堆积角有显著影响的参数。通过试验与参考相关文献,得到所需标定的9个参数取值如表1所示。
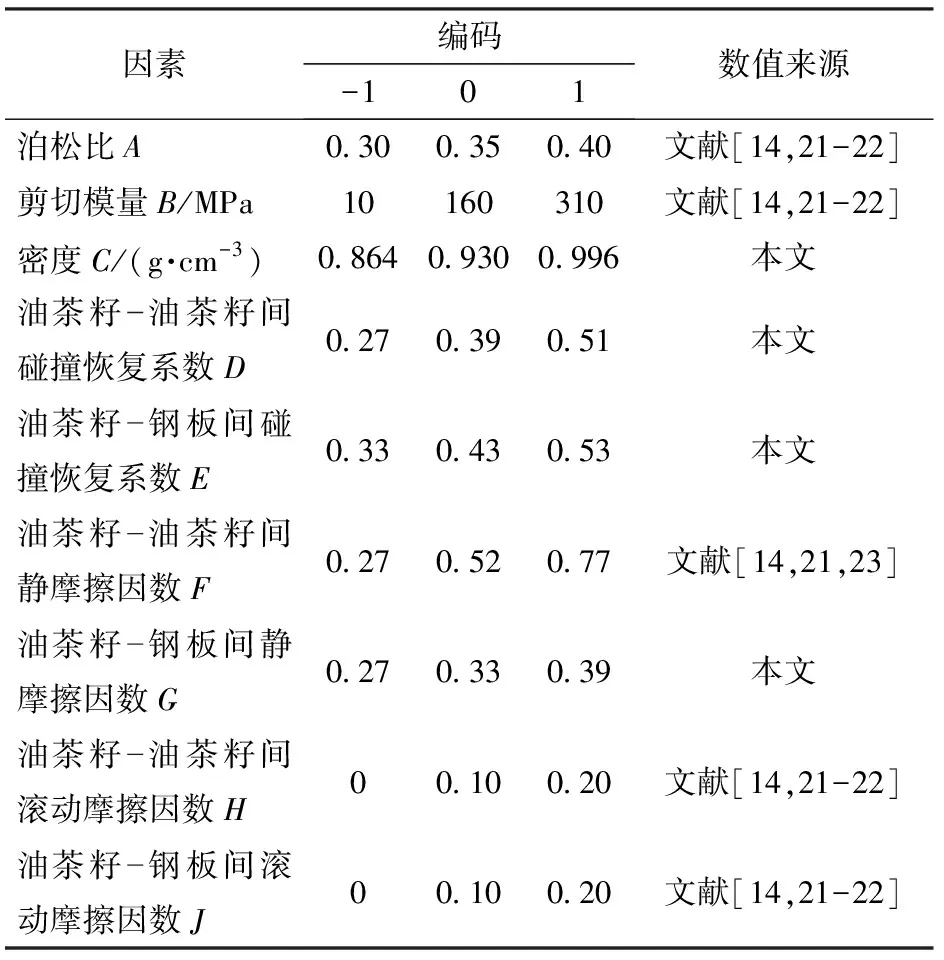
表1 PBD因素编码
(2)最陡爬坡试验
应用RSM分析方法建立回归模型求解最优值,其前提是因素的最优值在所选高低水平范围内,最陡爬坡试验可以较快地确定因素最优值所在区间。以PBD试验筛选显著性影响因素F、G和H,将其对应的水平区间等分为6份,非显著性参数选择中间水平,进行堆积角仿真试验。以最小相对误差为目标,确定中心组合RSM试验的上下限。相对误差计算式为
(5)
式中e——相对误差,%
y——实测油茶籽堆积角,(°)
z——仿真油茶籽堆积角,(°)
(3)中心组合响应面试验
综合最陡爬坡试验结果,采用中心组合响应面(Central composite design,CCD)试验进行RSM分析试验,以确定最优参数。将最陡爬坡试验结果范围作为上下限进行RSM试验,非显著性参数选择中间水平,显著性参数及仿真因素编码如表2所示。
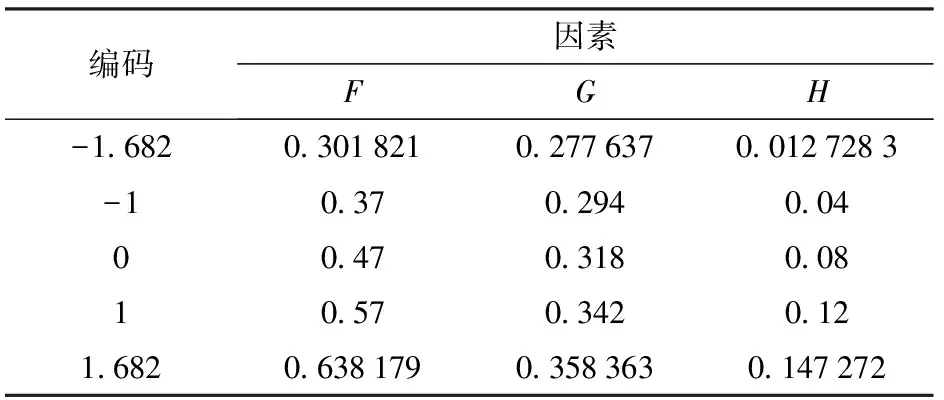
表2 CCD因素编码
1.4.2机器学习回归拟合建模
对RSM所用的相同数据,采用Matlab进行随机森林、SVR、BP、GA-BP回归拟合建模,寻找最优回归拟合算法。为了避免过度训练和过度参数化,将总数据(23组)随机分成17组(70%)进行训练,3组(15%)进行测试和3组(15%)用于验证[24-25]。选择mapminmax函数对输入和输出数据进行归一化处理,以消除量纲的影响。
(1)随机森林
随机森林回归通过随机抽取样本和特征,建立多棵相互不关联的决策树,通过并行的方式获得预测结果。设置决策树数目为100,最小子叶数为5。
(2)SVR
SVR是一种有监督的机器学习算法,使用对称损失函数进行训练。设置SVR类型为epsilon-SVR回归,损失函数为0.01,核函数为径向基函数,gamma函数值为0.8。
(3)BP
使用基于Levenberg-Marquardt算法和性能函数均方误差(MSE)的反向传播网络来训练网络[26]。隐含层和输出层的传递函数分别为Sigmoid函数和线性函数。规定训练的目标误差为0.001,设定学习速率为0.001,其中最大训练步数为50。
选择最优的拓扑结构是神经网络成功应用的关键。输入层设定3个神经元:油茶籽-油茶籽间静摩擦因数(F)、油茶籽-钢板间静摩擦因数(G)、油茶籽-油茶籽间滚动摩擦因数(H),油茶籽堆积角设定为输出层;隐含层的隐藏层节点个数s需要采用试错法来确定,隐藏层节点个数s计算式为
(6)
式中n、l——输入层和输出层神经元数
c——常数,取1~11[27]
根据式(6)计算s取值范围为3~13。
(4)GA-BP
由于BP存在对初始权值和阈值敏感,全局搜索能力差,容易陷入局部极小值等问题[28]。在执行BP神经网络之前,利用遗传算法对隐含层和输出层初始权值w1、w2,以及隐含层和输出层阈值b1、b2进行优化。调用遗传算法GAOT工具箱,通过选择、交叉和突变迭代优化个体的种群,把遗传算法优化后得到的初始权值和阈值赋值给BP神经网络进行学习更新,直到获得终止标准[29]。遗传算法参数设置为:进化迭代次数为300,种群规模为100,选择函数为几何规划排序选择(normGeomSelect)、系数为0.09,交叉系数为0.8,突变系数为0.2[30]。
1.4.3GA寻优
对于未知的非线性函数,仅通过函数输入输出数据难以精确寻找函数极值,所以结合遗传算法的非线性寻优能力,以建立的神经网络模型为遗传算法的适应度函数,以堆积角27.93°为寻优目标,对油茶籽-油茶籽间静摩擦因数(F)、油茶籽-钢板间静摩擦因数(G)、油茶籽-油茶籽间滚动摩擦因数(H)取值进行寻优。设定遗传算法的进化迭代次数为100,种群规模为200,选择函数为normGeomSelect、系数为0.8,交叉系数为2,突变系数为0.2。
1.4.4数据分析与处理
采用Design-Expert软件进行试验设计、数据处理与统计分析,算法运行平台为Matlab R2022a。
通过决定系数R2、均方误差(MSE)和平均绝对偏差(AAD)评估RSM和机器学习模型的预测性能[37],R2越大表明模型拟合度越高,MSE和AAD越低,表明模型精度和稳定性越好。
2 结果与讨论
2.1 PBD试验筛选显著性参数

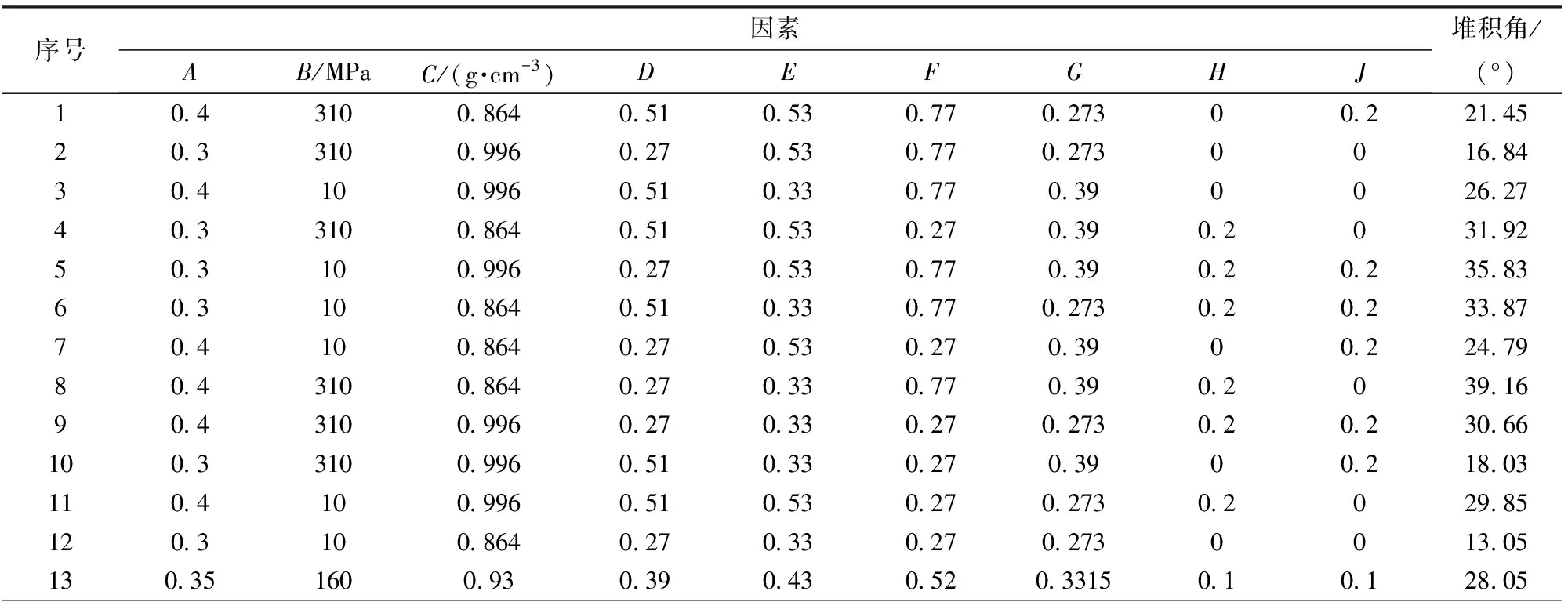
表3 PBD方案及结果

表4 PBD试验结果方差分析
2.2 最陡爬坡试验确定显著性参数最优值区间
根据PBD试验的结果,对堆积角的影响效果不显著的因素选用中间水平,即油茶籽泊松比0.35,剪切模量160 MPa,油茶籽-油茶籽间碰撞恢复系数0.39,油茶籽-钢板间碰撞恢复系数0.43,油茶籽-钢板间滚动摩擦因数0.10;根据试验测量结果,油茶籽密度为0.939 g/cm3;3个显著性参数(油茶籽-油茶籽间静摩擦因数、油茶籽-钢板间静摩擦因数和油茶籽-油茶籽间滚动摩擦因数)参考PBD试验因素水平表取值进行最陡爬坡试验,并计算油茶籽仿真堆积角与实际堆积角的相对误差,试验方案及结果如表5所示。

表5 最陡爬坡试验方案及结果
结果表明,随着油茶籽-油茶籽间静摩擦因数(F)、油茶籽-钢板间静摩擦因数(G)和油茶籽-油茶籽间滚动摩擦因数(H)的增大,油茶籽仿真堆积角也持续增大。同时堆积角的相对误差呈先减小后增大,其中第3组试验的相对误差最小,为10.89%,因此选择第3组试验所选的水平附近,即第2、3、4组试验所选的水平进行RSM分析试验,建立RSM回归模型。
2.3 RSM分析试验
CCD试验方案包括23个试验点,其中包括14个分析因子,9个零点估计误差,试验设计方案及响应值如表6所示。
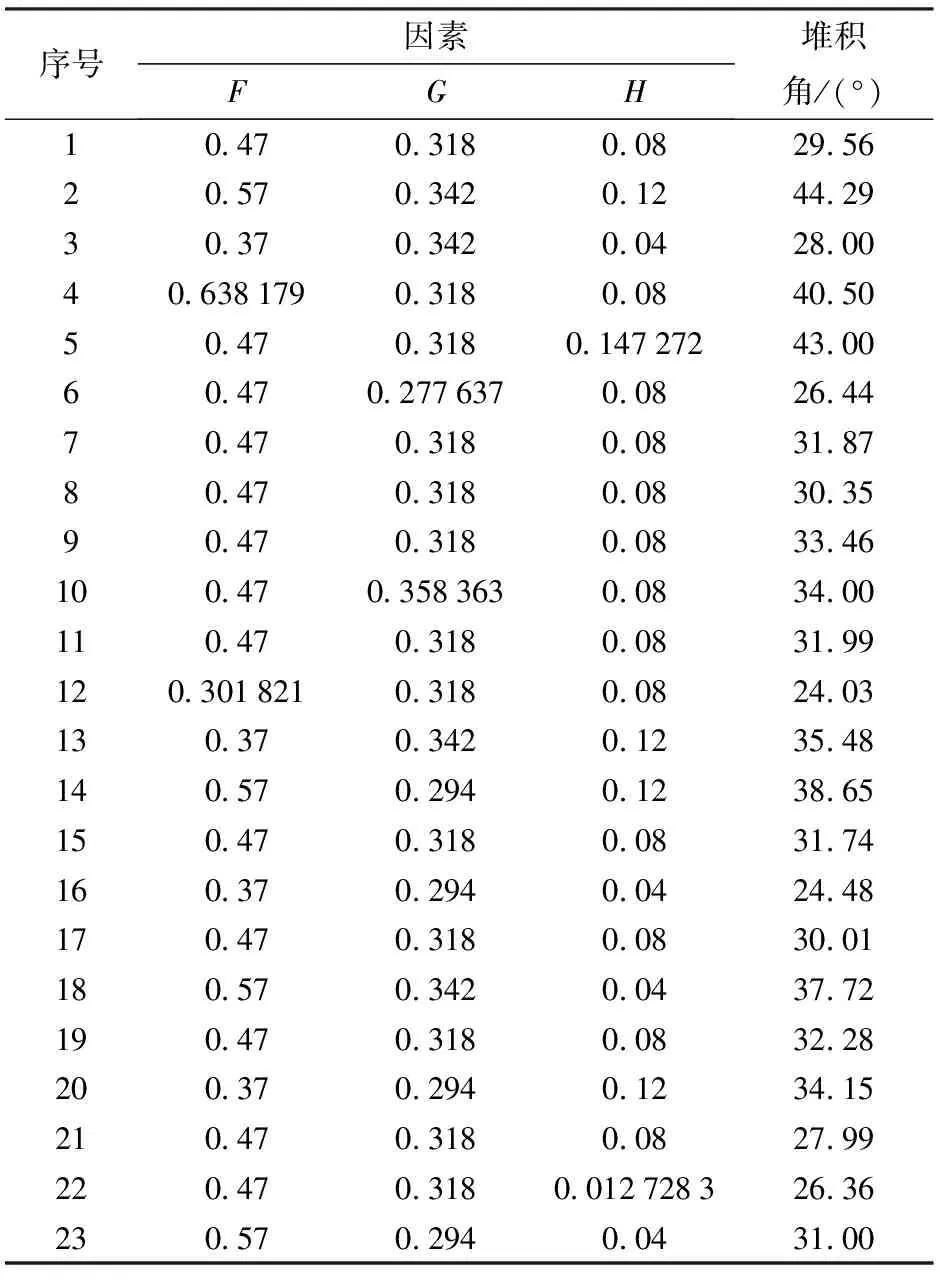
表6 CCD方案及结果
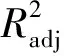
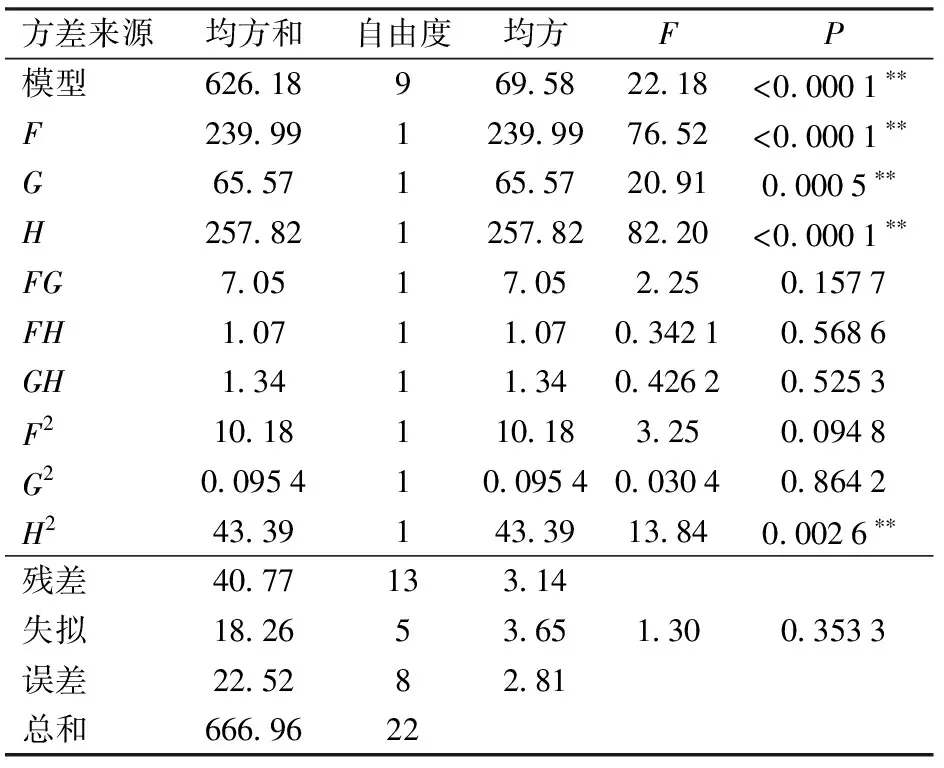
表7 CCD二次回归模型方差分析
剔除对二次回归模型影响不显著的因素,优化后的回归模型方差分析如表8所示,失拟项为0.342 3、精确度为25.10,较优化前所得回归方程的可靠性和精确性有改善。优化后回归方程为
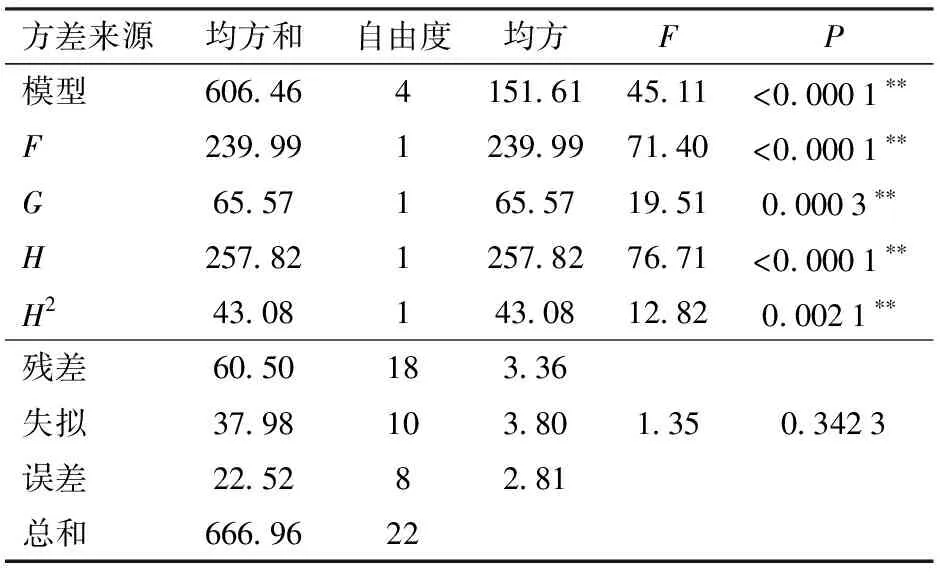
表8 CCD优化回归模型方差分析
α=-19.32+41.92F+91.30G-56.03H+
1 029.09H2
(7)
式中α——堆积角,(°)
2.4 交互因素对堆积角的影响
油茶籽-油茶籽间静摩擦因数(F)固定时,油茶籽-钢板间静摩擦因数和油茶籽-油茶籽间滚动摩擦因数的响应曲面如图7a所示,当油茶籽-钢板间静摩擦因数(G)不变时,堆积角随着油茶籽-油茶籽间滚动摩擦因数(H)增大逐渐增加,且变化趋势明显;当油茶籽-油茶籽间滚动摩擦因数(H)不变时,堆积角随着油茶籽-钢板间静摩擦因数(G)增大逐渐增加。
油茶籽-钢板间静摩擦因数(G)固定时,油茶籽-油茶籽间静摩擦因数(F)和油茶籽-油茶籽间滚动摩擦因数(H)的响应曲面如图7b所示,当油茶籽-油茶籽间静摩擦因数(F)不变时,堆积角随油茶籽-油茶籽间滚动摩擦因数(H)增大逐渐增加;当油茶籽-油茶籽间滚动摩擦因数(H)不变时,堆积角随着油茶籽-油茶籽间静摩擦因数(F)增大逐渐增加,两者变化趋势显著。

图7 交互因素对堆积角的影响
油茶籽-油茶籽间滚动摩擦因数(H)固定时,油茶籽-油茶籽间静摩擦因数(F)和油茶籽-钢板间静摩擦因数(G)的响应曲面如图7c所示,当油茶籽-油茶籽间静摩擦因数(F)不变时,堆积角随油茶籽-钢板间静摩擦因数(G)增大逐渐增加;当油茶籽-钢板间静摩擦因数(G)不变时,堆积角随油茶籽-油茶籽间静摩擦因数(F)增大逐渐增加。
2.5 机器学习回归模型对比
通过比较4种回归模型算法的R2、MSE和AAD,来确定能够适用后续试验的回归模型。对于BP来说,隐含层神经元数量较少容易导致模型欠拟合;数量过多可能会导致过拟合和训练时间过长,因此采用试错法对隐含层中的神经元数3~13进行研究。由于训练样本较少,回归拟合时会出现误差,因此重复训练5次,结果如表9所示。
由表9可知,SVR和GA-BP两种算法的预测能力比随机森林和BP更准。其中SVR的变异系数最小,拟合效果最稳定;但是SVR的R2(0.956 4)、AAD(0.099 1)和MSE(1.077 4)不及隐含神经元数为11的GA-BP网络,该网络具有最大的R2(0.960 1)、最小的AAD(0.099 4)和最小的MSE(0.898 4),并且其变异系数相对较小,即拟合效果较稳定。因此,选择11个隐含神经元的GA-BP为本研究的回归模型。由此,建立GA-BP模型的拓扑结构为3-11-1(图8)。

图8 GA-BP最优拓扑结构图
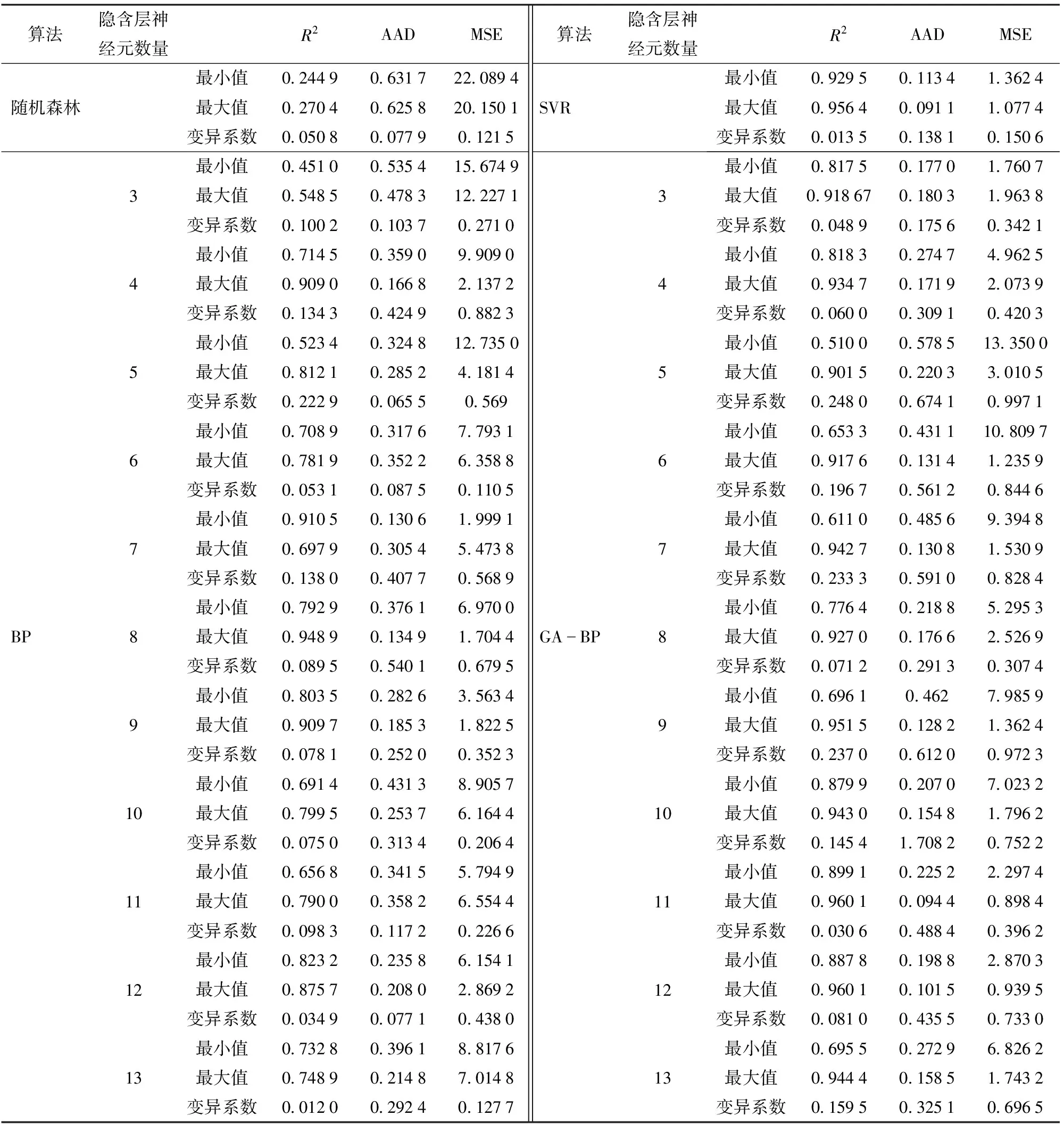
表9 机器学习回归模型对比
如图9所示,随着训练周期的增加,以训练组、验证组和测试组的MSE进行性能评价。MSE能够根据数据的变化程度衡量数据的平均误差,MSE越小,模型描述试验结果的精确度越好。在训练至第2步时获得了最佳验证性能,MSE为0.009 56,表示神经网络训练完成。因此,该GA-BP网络训练收敛速度较快且非常稳定,表明该模型能够较好地满足试验需求。
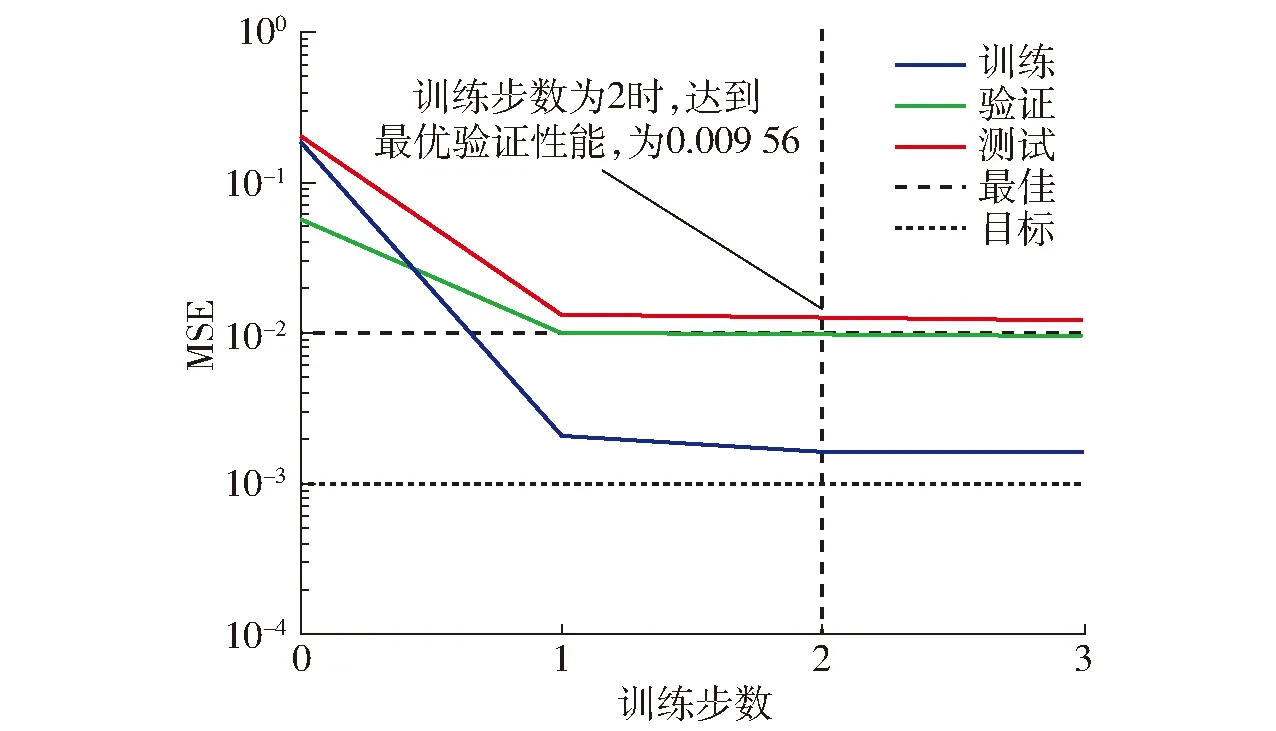
图9 性能曲线
在上述优化的基础上,得到了性能优良的神经网络模型。如图10所示,训练后分析显示,训练、验证、测试和所有数据相关系数R分别为:0.979 5、0.999 0、0.973 3和0.965 8,表明预测和实际数据之间具有良好的相关性。说明该神经网络模型能够适用后续的试验分析。
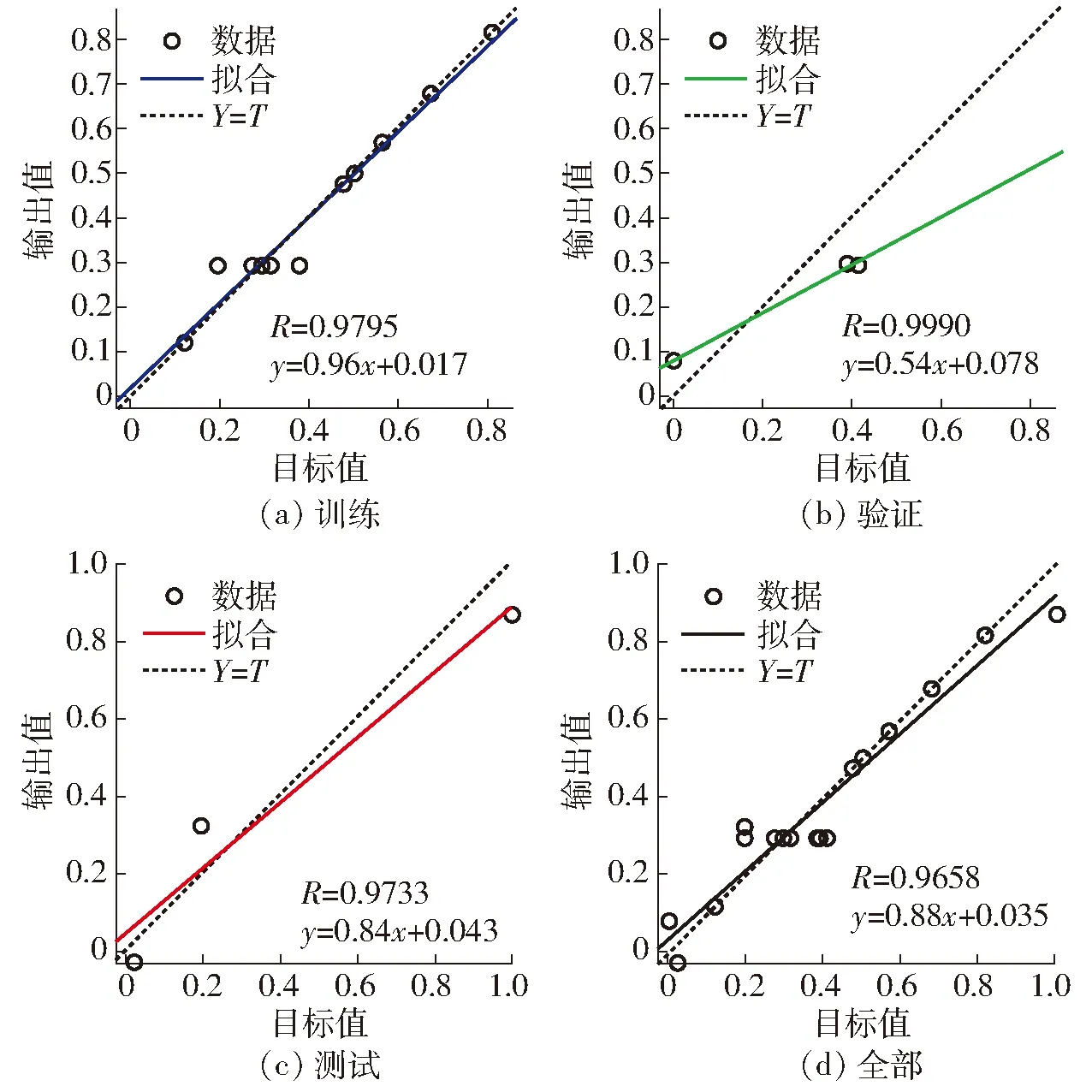
图10 回归分析结果
2.6 RSM和GA-BP-GA优化方法比较
图11为两种模型的实测值与预测值的对比。由图11可知两种模型均具有较好的拟合精度。GA-BP-GA模型的评价指标(R2=0.928 3,AAD为0.200 0,MSE为1.988 2)均优于RSM模型(R2=0.909 3,AAD为4.237 3,MSE为2.629 7),R2提高2.09%,AAD和MSE分别降低95.28%和24.39%。这表明GA-BP-GA模型预测能力优于RSM,具有较高的预测精度,这与前人研究结果相似[31-32]。
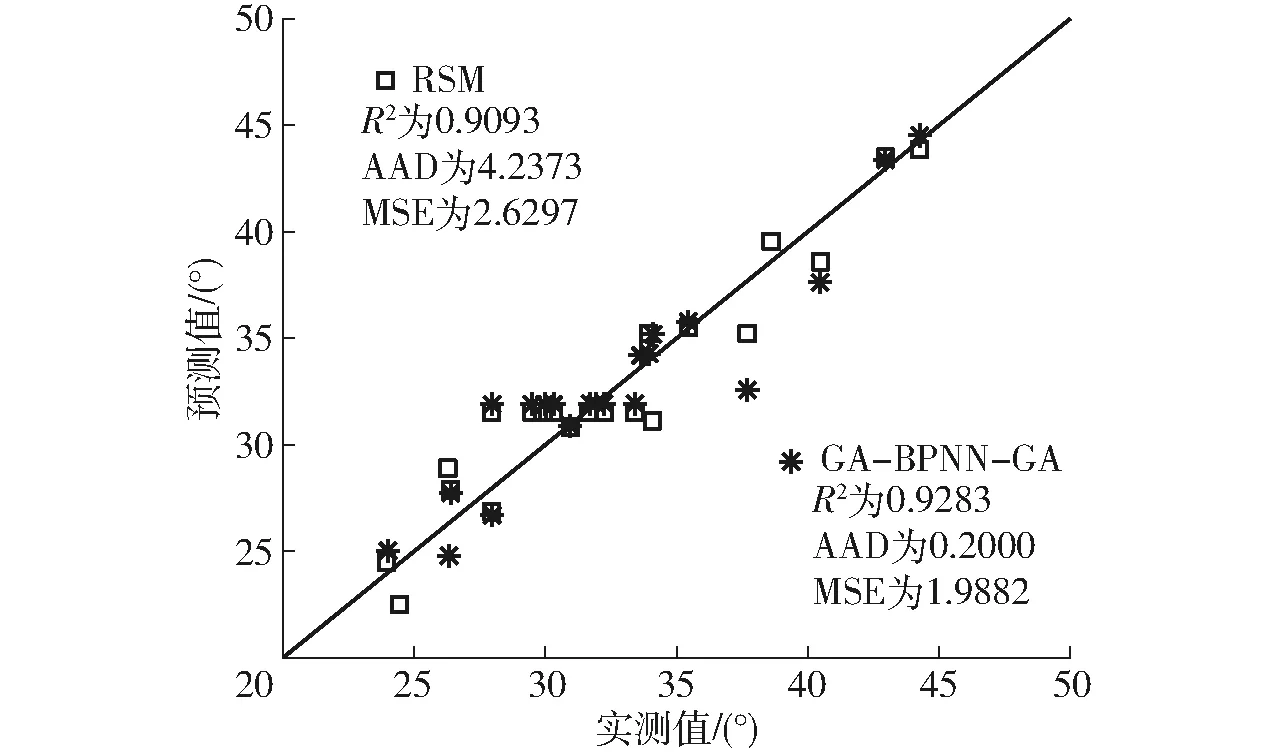
图11 RSM和GA-BP-GA方法的预测值与实测值
2.6.1RSM参数优化
应用Design-Expert软件以油茶籽实际堆积角平均值(27.93°)为目标,利用Numerical模块对回归模型进行优化求解,优化约束条件为
(8)
对得到的若干组解进行油茶籽堆积角仿真验证,得到与物理试验形状相近的一组最优解:油茶籽-油茶籽间静摩擦因数为0.383、油茶籽-钢板间静摩擦因数为0.335、油茶籽-油茶籽间滚动摩擦因数为0.064。测得油茶籽仿真堆积角为26.99°,与油茶籽实际堆积角的相对误差为3.33%。
2.6.2GA-BP-GA参数优化
图12为随进化代数变化的适应度变化曲线。最初GA利用其群体搜索特性使得被选择个体的适应度骤降;随后,GA进行多次的交叉和选择处理,被选择个体的适应度产生小范围的正向改变,逐步向目标值靠近;当进行到第42次选代时,适应度曲线逐渐收敛于0附近,这表明预测值与目标值之差极小;通过多次循环选代,当进化迭代次数达到目标值100时,GA停止选择并得出适应度最接近的个体。运行得到的最优参数:油茶籽-油茶籽间静摩擦因数为0.443、油茶籽-钢板间静摩擦因数为0.319、油茶籽-油茶籽间滚动摩擦因数为0.063。测得油茶籽仿真堆积角为27.63°,与油茶籽实际堆积角的相对误差为1.09%。
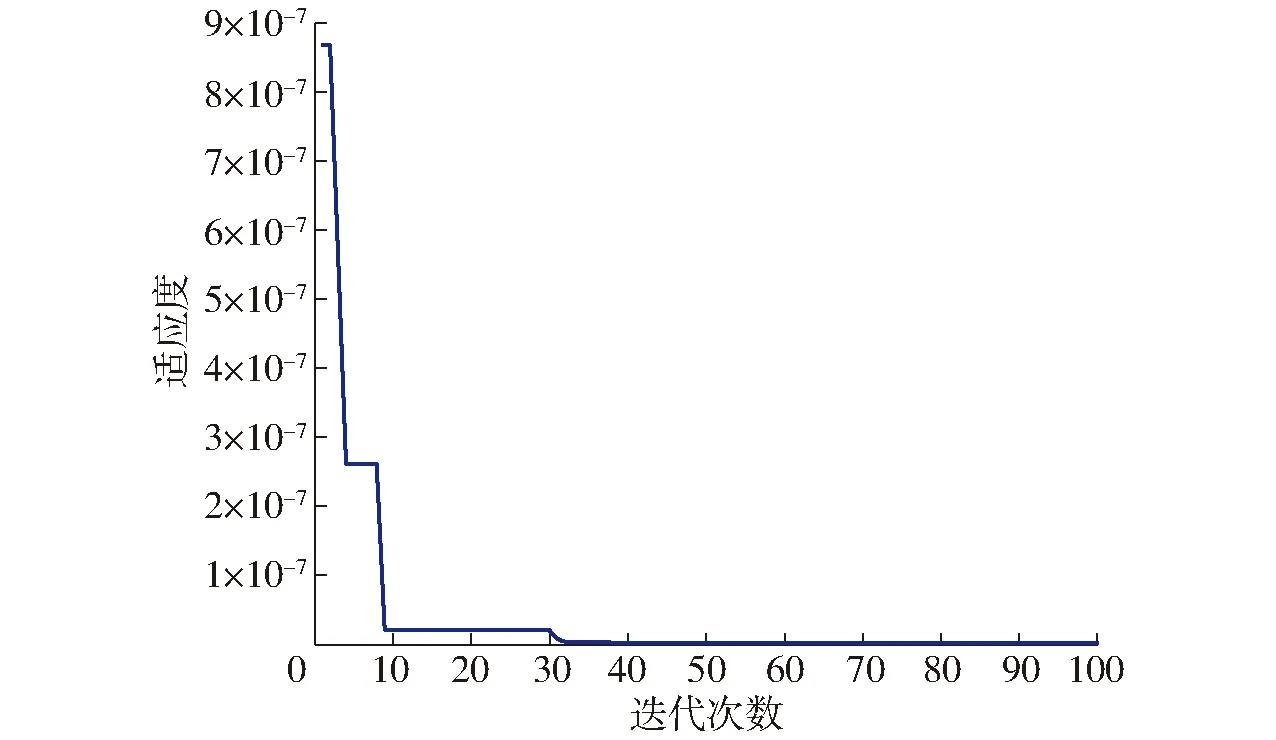
图12 适应度变化曲线
两种模型堆积角预测误差均小于5.00%,说明所得3个显著性参数的最优值准确可靠,两种方法均可用于堆积角预测。而GA-BP的预测精度高于RSM,并且GA-BP-GA寻优后的堆积角预测误差比RSM更小,表明GA-BP-GA的预测结果与真实值更接近,这与其他工艺优化结论一致[27,30,33]。
2.7 验证试验
仿真试验与物理试验对比如图13所示,两者油茶籽颗粒堆轮廓接近,表明仿真堆积角与物理堆积角试验休止角无显著性差异,该研究所建油茶籽模型与参数标定结果可用于离散元仿真研究。

图13 参数标定的物理试验与仿真试验对比
3 结论
(1)采用逆向工程技术提取了4种形状油茶籽的轮廓,并在EDEM软件中通过自动填充方式,建立了填充球形颗粒的油茶籽离散元模型。
(2)通过物理试验测得油茶籽的堆积角为(27.93±1.46)°,以及密度、碰撞恢复系数和油茶籽-钢板间静摩擦因数的参数区间,采用PBD试验和最陡爬坡试验筛选出影响堆积角的显著性因素(油茶籽-油茶籽间静摩擦因数、油茶籽-钢板间静摩擦因数、油茶籽-油茶籽间滚动摩擦因数),并进一步缩小显著性参数取值范围。
(3)比较了随机森林、SVR、BP和GA-BP 4种机器学习回归模型的R2、AAD、MSE及变异系数,当隐含层神经元数为11时,GA-BP的R2(0.960 1)最大、AAD(0.099 4)和MSE(0.898 4)最小,并且其变异系数相对较小,表明其预测能力和拟合稳定性较高,由此建立了拓扑结构为3-11-1的GA-BP回归模型作为油茶籽堆积角预测模型。
(4)采用遗传算法对GA-BP回归模型进行反函数寻优,得到油茶籽-油茶籽间静摩擦因数为0.443、油茶籽-钢板间静摩擦因数为0.319、油茶籽-油茶籽间滚动摩擦因数为0.063,测得仿真堆积角为27.63°,与实际堆积角的相对误差为1.09%,优于RSM的相对误差(3.33%)。表明在油茶籽参数标定中,GA-BP-GA的参数优化效果优于RSM,并且该研究所建油茶籽模型与参数标定结果可用于离散元仿真研究。

