基于改进复合三角函数的伺服压力机轨迹规划研究

徐道春 吕明青 邵珠峰 陈涵玉 胡益玮 王传英

(1.北京林业大学工学院，北京 100083；2.北京林业大学林业装备与自动化国家林草局重点实验室，北京 100083；3.清华大学摩擦学国家重点实验室，北京 100084；4.清华大学精密超精密制造装备及控制北京市重点实验室，北京 100084；5.济南二机床集团有限公司，济南 250022)

0 引言

随着汽车工业的高速发展，高强度钢板、铝合金板材、非等厚拼焊钢板等在汽车中的应用日益普及。机械压力机的滑块运动特性单一、柔性差，难以适用不同材料的冲压成形工艺。伺服压力机是基于伺服控制技术的一种新型冲压成形设备，可灵活调整滑块的运动曲线，能够满足不同材料的多种成形工艺要求，具有加工柔性好、成形精度高、节能增效等特性[1-2]。同时，大型伺服压力机滑块等主传动部件的惯性较大，且速度变化剧烈，合理的运动轨迹能有效降低系统能耗，提高加工精度[3]。伺服压力机主传动机构轨迹规划的重点是主驱动伺服电机的加减速控制。

目前加减速控制算法主要包括S形曲线加减速[4-8]、多项式加减速[9]、三角函数加减速[10]、NURBS曲线[11]、Bezier曲线[12-14]、B样条曲线[15-16]等。其中，S形曲线加减速存在加加速度突变，三角函数和多项式加减速满足加速度和加加速度连续的要求，避免了加工的柔性冲击[17]，NURBS和B样条曲线具有局部可调性，使对关键点的建模更灵活，但会在求解中导致最优关键点的不唯一，Bezier曲线的每个控制点均影响曲线形状，求解复杂。郝齐等[6]采用S形曲线优化了轨迹的最大加速度，降低了最大驱动力及对电动机的要求。刘志峰等[7]采用五阶段S形曲线优化了加加速度幅值来抑制同步带传动印刷机系统的扭振。张相胜等[8]将传统S形曲线加减速控制模型的加加速度变化规律设计为三角形状，以此解决算法本身存在的加加速度阶跃的问题。宋清玉等[18]采用2个不同周期的三角函数叠加进行加减速模型构造，从而降低对电动机功率的要求，但该算法固定了变速区间的时间占比。

在伺服压力机拉深工艺的轨迹规划中，压力机质量最大的运动部件滑块做变速运动时所产生的惯性力会造成较大的振动，进而影响冲压件的精度与模具的寿命。生产节拍即一个冲压周期完成的冲压件数量，直接影响生产效率。为了降低压力机滑块的变速冲击，提高冲压件的精度和模具寿命，QU[12]和尚万峰等[13]以滑块加速度和加加速度峰值最小化为优化目标，降低了滑块的加速度从而降低其惯性力对冲压件的冲击。SONG等[19]以实现冲压生产节拍最高为优化目标，缩短了伺服压力机的冲压周期，提高了生产效率。上述研究重点关注冲压工作段的轨迹，分别研究了避免冲击和提高效率等方面，但是缺乏综合性能和能耗优化的考虑，大型伺服压力机频繁的加减速变化和克服工件的变形所需的能量完全由伺服电机提供，从而使伺服电机的能耗巨大，因此本文将降低能耗考虑在优化目标中以降低生产成本。

本文对大型伺服压力机高效拉深工艺模式进行研究，首先需通过建立包含关节摩擦力的高精度动力学模型以保证后续轨迹规划建模的精确性，同时为实现提高伺服压力机的生产节拍要求，对现有的伺服电机柔性加减速控制方法进行改进。在此基础上，为同时降低伺服电机的能耗，综合冲压生产节拍最大化和能耗最低为优化目标，建立大型伺服压力机高效拉深工艺轨迹优化设计数学模型，并研究该优化问题的求解方法，以期完成伺服压力机电机转速优化和滑块轨迹规划。

1 伺服压力机拉深工艺模式

研究的六连杆式伺服压力机结构如图1所示，其主传动机构及简图如图2和图3所示，曲柄为主动杆件，三角杆起到调速作用，偏心轮与三角杆中点为摇杆。

图1 六连杆伺服压力机

图2 六连杆主传动机构

图3 六连杆主传动机构简图

主驱动伺服电机通过传动机构驱动下方滑块进行冲压工作，其工序成型能量为800 kJ，公称力为8 500 kN的行程为8 mm，载荷作用范围为0～250 mm。通过前期研究的运动学建模和遗传算法优化得到机构尺寸。针对机构运动稳定性、传力性能、位置精度及增力特性进行分析，以滑块速度波动、压力角、侧向力和机构的机械增益为优化性能指标，通过统一量纲和线性加权的方式构造出反映综合性能的多目标优化函数，引入几何以及行程约束，并添加压力机的工作空间和杆件不干涉等约束条件，采用遗传算法完成多目标优化设计，如图4～7所示。由图4～7可知，其尺寸优化后，机构运动稳定性更好、侧向力减小即对滑块位置精度影响更小、传力性能及增力特性更优。从传动机构的基本结构构型进行尺寸优化设计，利于压力机基本的运动性能提升，同时为了充分发挥伺服压力机高能效和高效率的优势，需对伺服电机加减速控制和其滑块的运动轨迹进行规划。以优化后尺寸为基础，建立包含关节摩擦力的高精度动力学模型。

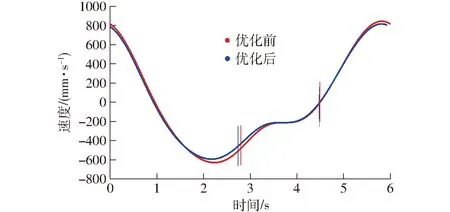
图4 滑块速度曲线

图5 滑块侧向力曲线

图6 机械增益曲线

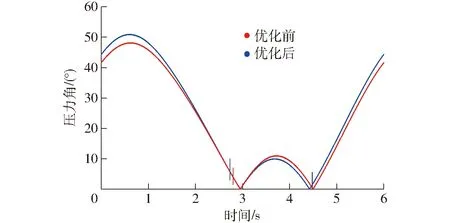
图7 滑块处压力角曲线

伺服压力机工艺模式分为4个阶段[19-20]，如图8所示，空载高速向下进给Ⅰ，工作行程匀速向下运动Ⅱ，空载快速返回Ⅲ，曲柄低速运行段Ⅳ，t41为机械手取件并传输所需的安全时间。

图8 伺服压力机运动分相图

由关键点进行控制，关键点1：设置滑块闭合角θ1，据此可得滑块下移高度s1。θ1为让机械手安全离开压力机时的曲柄转角，对应的s1是机械手离开需要的高度空间。关键点2：设置冲压起始的转速N2以及需要的冲压起始角θ2，并根据方程计算出对应滑块高度s2以及滑块速度v2。关键点3：设置冲压结束转速N3以及冲压结束角θ3，同样计算出对应滑块速度v3，以及冲压结束时滑块高度s3。关键点4：设置滑块开启角θ4，据此计算出该角度下滑块所处的高度s4。

为了提高生产效率，伺服压力机通常采用连续工作模式。即在机械手传输时伺服电机低速运行，而不是停在上死点处。因此工作段Ⅱ需要滑块匀速冲压，非工作段Ⅰ和Ⅲ为高速运动段，提高生产节拍，非工作段Ⅳ为低速运动段，为机械手传输冲压件留出时间。伺服压力机的连续工作模式避免了伺服电机频繁启停操作。

2 动力学分析

2.1 动力学建模

对该伺服压力机的六连杆系统进行动力学分析，如图9所示。采用达朗贝尔原理，引入惯性力建立各杆的力和力矩平衡方程，建模中考虑滑块自接触板料时输出的工作载荷压力F、曲柄扭矩M、滑块下方所受气压装置平衡力Fp、滑块处摩擦力、各转动关节摩擦力和力矩。

图9 六连杆机构的动力学受力图

在大型机械传动中，关节间的摩擦损耗不可避免，并且对能耗的影响很大。因此在动力学建模中考虑关节间摩擦。在压力机主传动六连杆机构中，摩擦主要是由于关节铰链之间的转动和滑块移动产生，故在此机构的动力学分析中，将关节间摩擦力用“库伦-粘性”摩擦模型进行计算，使模型更接近实际情况。

以杆OA为研究对象，对其进行受力分析可得

F11x+F12x+f11sinθ11+f12sinθ12=

-m1at1sinθ1-m1an1cosθ1

(1)

F12y+F11y-m1g-f11cosθ11-f12cosθ12=

m1at1cosθ1-m1an1sinθ1

(2)

考虑平衡力矩，计算得

M-(F12x+f12sinθ12)r1sinθ1+

(F12y-f12cosθ12)r1cosθ1-m1gRC1cosθ1=Jz1α1

(3)

其中at1=α1RC1=α1λC1r1

式中RC1——杆OA质心到转动中心O的距离

Jz1——杆OA绕点O的转动惯量

F11x——杆OA在转动副O处所受力的水平分量

F11y——杆OA在转动副O处所受力的垂直分量

F12x——杆OA在转动副A处所受力的水平分量

F12y——杆OA在转动副A处所受力的垂直分量

m1——杆OA质量

f11——点O处关节摩擦力

f12——点A处关节摩擦力

θ11——合力F11与X轴的夹角

α1——杆OA角加速度

ω1——杆OA角速度

λC1——杆OA质心位置系数

r1——杆OA长度

θ12——合力F12与X轴的夹角

an1——杆OA法向加速度

at1——杆OA切向加速度

η11——杆OA在转动副O处的粘性摩擦系数

η12——杆OA在转动副A处的粘性摩擦系数杆BC和杆DE的分析过程类似，不再赘述。

以三角杆ABD为研究对象，对其进行受力分析可得

F56x+F23x-F12x+f56sinθ56-

f12sinθ12+f23sinθ23=m2ax2

(4)

F56y-F12y+F23y-f56cosθ56+

f12cosθ12-f23cosθ23=m2ay2

(5)

考虑平衡力矩，计算得

-(F23x+f23sinθ23)r2sinθ2+(F23y-f23cosθ23)r2cosθ2-

(F56x+f56sinθ56)r5sinθ5+(F56y-f56cosθ56)r5cosθ5-

m2gRC2cos(θ2+γ1)=Jz2α2

(6)

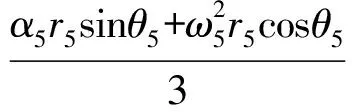
式中m2——三角杆ABD质量

γ1——杆BD的中线与杆AB的夹角

μ23——杆BC在转动副B处的粘性摩擦系数

μ56——杆DE在转动副D处的粘性摩擦系数

η23——杆BC在转动副B处的库伦摩擦系数

η56——杆DE在转动副D处的库伦摩擦系数

RC2——三角杆ABD质心到转动中心A的距离

Jz2——三角杆ABD绕点A的转动惯量

θ2——杆AB与X轴夹角

r2——杆AB长度

θ5——杆AD与X轴夹角

r5——杆AD长度

f23——点B处关节摩擦力

f56——点D处关节摩擦力

θ23——合力F23与X轴的夹角

θ56——合力F56与X轴的夹角

ax2——三角杆ABD质心加速度的水平分量

ay2——三角杆ABD质心加速度的垂直分量

以滑块E为研究对象，对其进行受力分析可得

F67x+f67sinθ67=Fn

(7)

Fp+F-m7g+f67cosθ67-F67y+f77=-mia

(8)

其中

f77=μ77Fnsgn(v)

mi=λmiρr(i=1,2,3,6,7)

Fp=(λ1m1+λ2m2+λ3m3+λ6m6+λ7m7)g

式中λi——平衡力系数

ρ——杆系材料线密度

λmi——杆系质量系数

m3——杆BC质量

m6——杆DE质量

m7——滑块质量

f77——滑块处滑动摩擦力

v——滑块速度

a——滑块加速度

θ67——合力F67与X轴的夹角

2.2 模型参数选取

建立的杆系动力学方程中包含杆系质量、关节摩擦系数、平衡力和工作段载荷模型等影响参数。因此需要对这些模型参数进行合理地选择和辨识，以提高系统优化的准确性。

2.2.1杆系质量

伺服压力机制造过程中，杆系材料一般为45钢或Q235，其材料密度为7 800～7 850 kg/m3。查阅现有的压力机图纸，近似认为杆件的线密度为500 kg/m。而实际伺服压力机由4个结构相同、空间位置对称的杆系组成，所以在计算中取杆件线密度为2 000 kg/m。对于六连杆当中的三角杆，由于其实心的三角形结构，且上面附有质量较大的偏心轮，因此在计算时乘以系数λm2。查阅已有的三角杆图纸并计算其质量，取λm2=12。

2.2.2关节摩擦系数

选用“库伦-粘性”摩擦模型对各转动副关节进行动力学建模，摩擦力为f=μN+ηωr，其中的库伦摩擦系数μ和粘性摩擦系数η都需要根据实际情况进行合理的取值，以确保模型尽可能地贴合实际。

曾宇翔[21]曾对伺服压力机杆系动力学中的摩擦力进行了系统性的建模与分析，并利用实验数据对库伦-粘性摩擦系数进行了辨识。根据其研究成果，本文库伦摩擦系数μ取0.1，粘性摩擦系数η取0.25。

2.2.3平衡力

为了消除杆系质量和转动副间隙对压力机工作性能的影响，保证传动机构平稳运动，压力机通常会使用平衡器对重力进行平衡。在此次建模中，近似认为平衡力作用在滑块上，其大小恒定，为Fp=λ∑mig。其中λ为平衡系数，需要根据实际情况和仿真结果进行选取。图10为不同平衡系数下的曲柄转矩，可以看出随着平衡系数的改变，非工作段内的曲柄转矩会受到较大影响。在与实际的工作数据进行比对后，选择平衡系数λ=0.95。

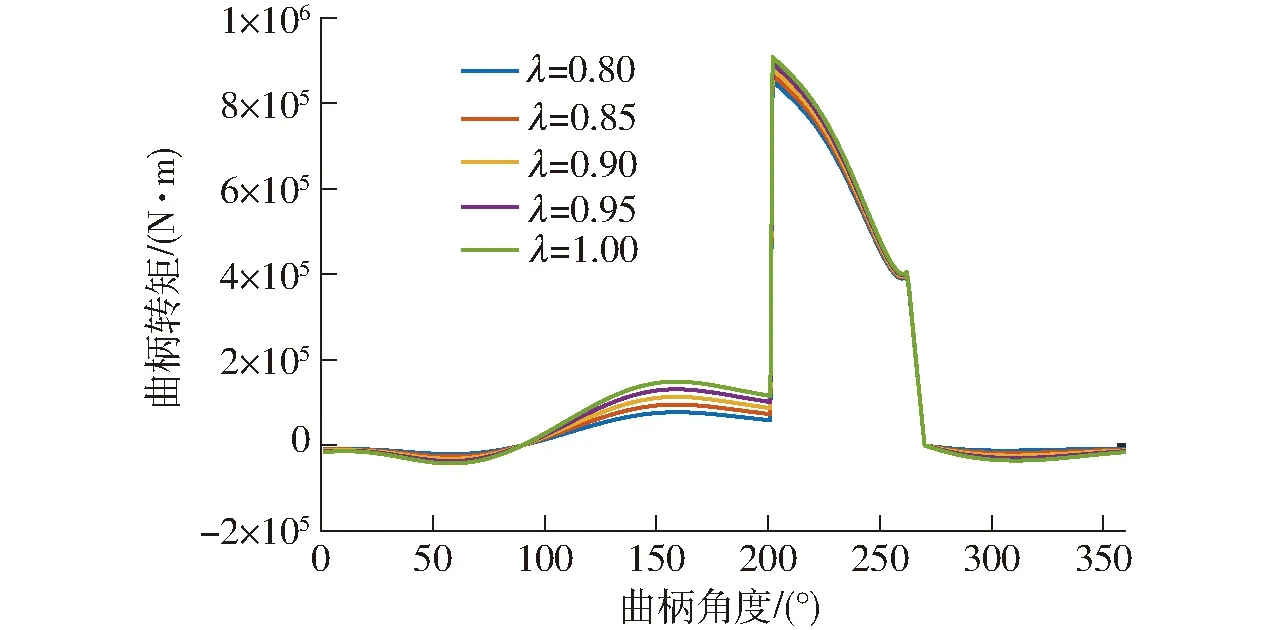
图10 不同平衡系数对曲柄转矩的影响

2.2.4载荷模型

在工作段，滑块会受到巨大的工作力，而工作力会随着与下死点距离发生改变。在板料成型的过程中，通常认为对于同种材料、同一个模具来说，板材变形的能量是固定的，由此再根据实际测量的部分关键点工作力数据，可以推导工作载荷的近似模型。原载荷模型分段采集呈阶梯状，由于存在一定的间断点，并不能完全贴合实际情况。在考虑到实际问题的性质，选用F(s)=asb+c作为载荷模型，由载荷参数得边界条件为

(9)

解得F(s)=46 779s-0.97+2 279.5(kN)。图11为修改前后载荷模型的载荷，从图11中可以看到，修改后载荷模型能够在有效贴合实际情况，同时提高了模型光滑性，有利于后续计算和优化。

图11 不同载荷模型载荷对比

3 伺服电机转速优化及滑块轨迹规划建模

3.1 复合三角函数加减速控制模型改进

加减速过程采用复合三角函数进行建模，即采用两个不同周期的三角函数叠加作为伺服电机加减速的构造函数，如图12所示。宋清玉等[18]采用加速区间分阶段的x为0.25的加减速曲线，并成功降低了系统对伺服电机功率的要求，在此基础上，对占比进行优化以获得更加良好的转速曲线。

图12 复合三角函数的角加速度示意图

函数角加速度方程为

(10)

通过积分得到角速度函数为

ω(t)=

(11)

根据边界条件ω(0)=ω1,ω(t0)=ω2，以及函数连续的条件，求解得

(12)

因此角速度表达式为

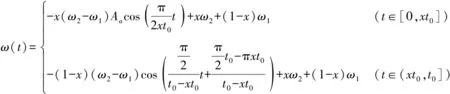
(13)

对式(13)进行积分，求解角度随时间变化的关系，同时代入边界条件进行计算，最后得到

(14)

同时有

(15)

伺服电机在工作过程中的角速度曲线如图13所示。根据θ1、θ2、θ3、θ4确定选取的角速度极值角度范围即θ12、θ34、θ41。其中，θ1、θ2、θ3、θ4以及ω2、ω3为已知参变量，而其余3个极值位置角度θ12、θ34、θ41，角速度ω12、ω34、ω41，5个角度θ12、θ2、θ3、θ34、θ41之间的x12、x23、x34、x45、x51取值为需要优化的参变量。

图13 伺服电机整周工作的角速度曲线及关键点

3.2 滑块轨迹规划约束条件

(16)

(17)

式中tc——伺服压力机冲压周期

u——传动比

电机要满足T(Nmean,Trms)≤T(Sl)，前者为伺服电机实际热极限点，后者为伺服电机理论热极限曲线。

3.3 滑块轨迹规划目标函数

为实现效率与能耗的综合优化，确定综合优化目标函数为

(18)

其中

T=t12+t23+t34+t41

式中W——压力机周期能耗

w1、w2——权重

T——压力机周期节拍时间

Wmax=5.4×106J，Tmax=6 s，w1、w2在此优化中均取0.5，视为二者的优化效果相当，可根据实际需求进行调整。

4 优化结果分析

采用上述数学模型和遗传算法[22]进行电机转速和滑块轨迹的优化，得到优化结果如表1所示。

表1 六连杆伺服电机的转速轨迹参数

由表1取由目标函数得到的优化值，求解过程如图14所示。

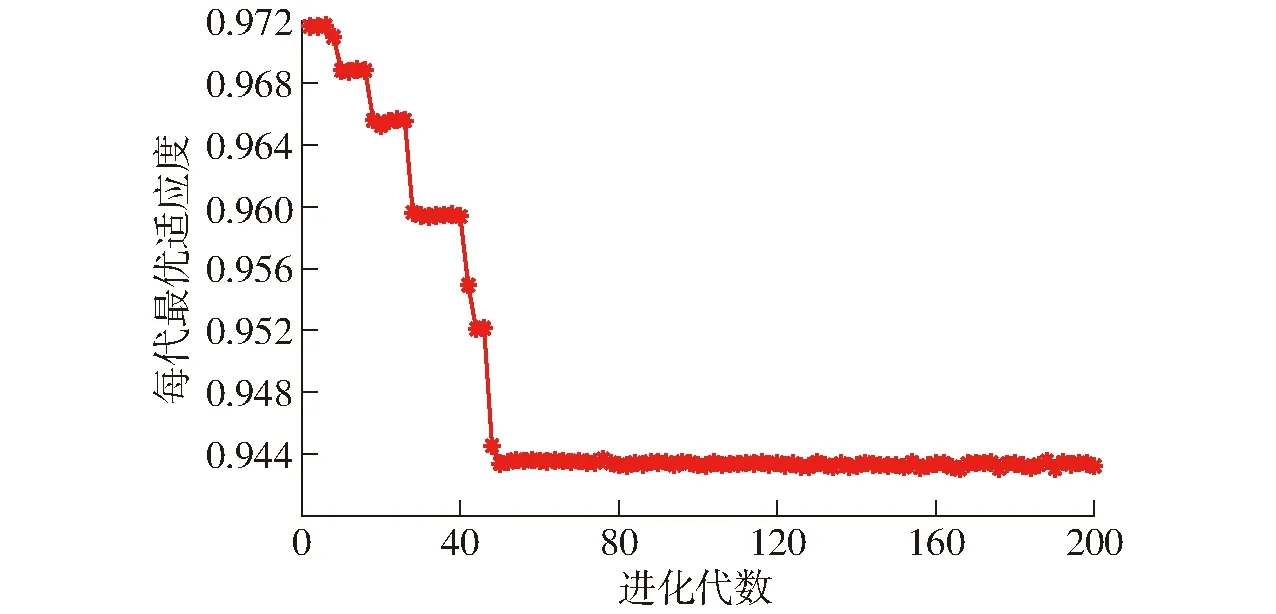
图14 多目标求解过程图

将表1优化后的数值建模得到电机优化后的曲柄转速和能耗对比见表2。

表2 目标值对比

优化前后生产节拍时间如图15所示，其时间减小3.23%。

图15 曲柄角速度曲线

优化前后曲柄转矩如图16所示，其能效提升4.54%。

图16 曲柄转矩曲线

图17为伺服电机在一个冲压周期内的动态限和热极限校核结果，伺服电机理论加载转矩和热极限点满足边界要求，伺服电机校核结果安全。

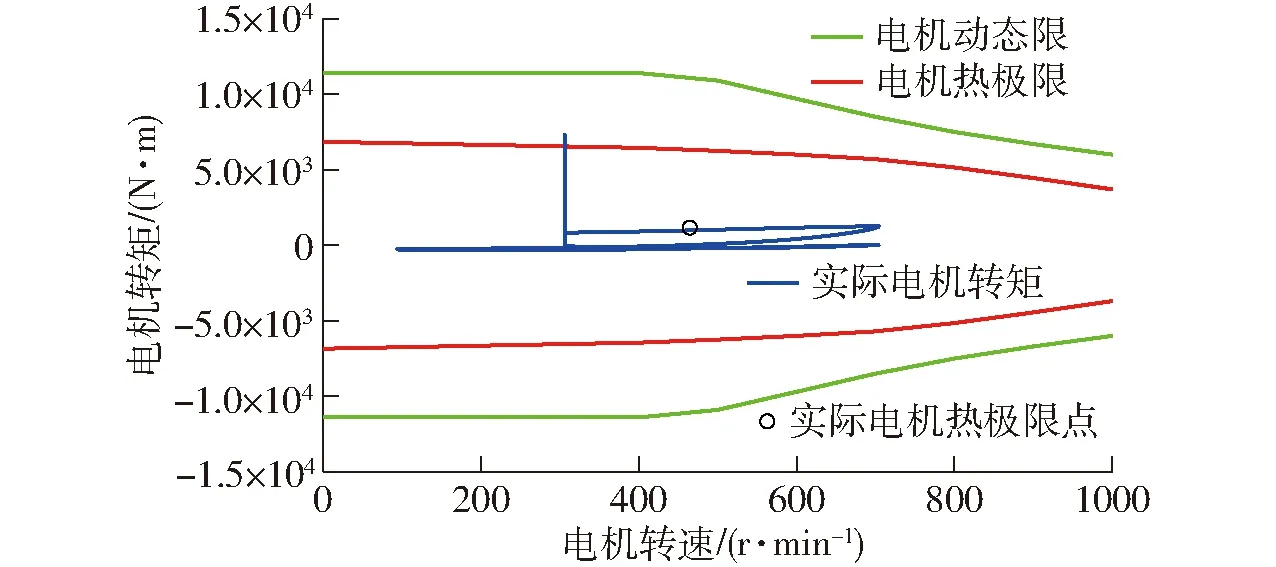
图17 伺服电机动态限和热极限校核结果

5 结论

(1)建立了伺服压力机主传动机构的动力学模型，以库伦-粘性摩擦模型为基础考虑了其关节摩擦力，同时完善了滑块处的工作载荷模型，提高了模型的准确性。

(2)改进了基于复合三角函数的伺服电机柔性加减速控制模型，既保留曲柄转速、加速度和加加速度变化连续的优势，避免了加减速过程对伺服压力机的柔性冲击,又优化了变速区间的时间占比，提高了生产效率，可用于伺服压力机拉深轨迹规划。

(3)建立了大型伺服压力机高效拉深工艺轨迹规划数学模型，提出了综合冲压生产节拍最大化和能耗最低的优化目标，并提出了更全面有效的实际工程约束条件，优化结果表明，滑块运动轨迹更优。