测风激光雷达光学参量对相干效率的影响

彭 涛,王 茜,石 磊,姜 勇,陈 涌,周鼎富

(西南技术物理研究所,成都 610041)

引 言

激光雷达(light detection and ranging,LiDAR)作为一种常用光学遥感设备在风场测量应用中扮演着愈发重要的作用[1-9]。相干测风技术通过本振光与大气后向散射信号光的拍频获取大气气溶胶的多普勒频移信息,从而实现风速测量。相较直接探测方式,其具有高增益、小体积、激光器指标易实现等优点,是远程测风的通用手段。相干效率表征了接收的信号光光场与本振光光场之间的匹配程度,是相干探测模式下的关键指标。系统中激光器、探测器、光学天线等关键光学单元的性能参数,以及大气扰动程度直接影响相干效率的大小。目前,相干测风激光雷达正朝着远程、小型化、低成本的趋势发展[10-12],对关键器件的优化设计提出了更高的要求,因此,研究测风激光雷达光学参量对相干效率的影响具有重要意义。

相干测风激光雷达的相关技术在国内外得到了广泛研究。AUGERE等人将全光纤相干多普勒测风雷达搭载于机载平台进行了挂飞测量,水平探测距离为3 km,垂直距离分辨率100 m[13]。WITSCHAS等人基于重力波研究开展了机载激光测风雷达的飞行试验,测量数据经比对,风速均方根误差小于0.2 m/s[14]。WANG等人提出了相干多普勒测风雷达联合时频算法,与传统快速傅里叶变化法相比,提升了系统时空分辨率、信噪比和最大测程[15]。MARTIN等人针对脉冲相干激光雷达系统,研制了小型化集成电路,配合信息处理算法实现了小能量远距离的硬目标探测[16]。CLEMENT等人利用频移环自相关处理法实现了1550 nm激光相干探测系统发射光束的脉冲压缩[17]。HAYLOCK等人研制了微型亚微秒电光开关,并应用于近程激光相干测速系统[18]。以上研究主要集中于对相干测风激光雷达相关试验结果进行分析,或是对风场反演和信息处理算法进行优化,但是对于光学系统的设计仿真鲜有报道,无法从理论上分析不同湍流条件下重要光学参量对系统性能指标的影响。

本文中针对相干测风激光雷达,首先概述了光学系统的组成和工作原理,然后基于光场叠加法讨论分析了关键光学参量对系统相干效率的影响,最后针对不同参量开展了整机性能验证实验,可为激光器、光学天线、接收器件的设计优化提供理论支撑。

1 相干测风光学系统

相干测风光学系统如图1所示。1550 nm半导体激光种子器发射几百赫兹线宽的激光,经1×2光纤分束器分束后,一路作为本振光(local oscillator,LO),频率为f0,输入光纤耦合器;另一路经声光调制器(acousto-optic modulator,AOM)调制成脉冲激光,频率为f0+f1,再经脉冲掺铒光纤放大器(erbium-doped fiber amplifier,EDFA)放大输出,然后经光学环行器和天线射向目标空域。激光与大气气溶胶作用后产生多普勒频移,后向散射信号光频率为f0+f1+f2,依次经天线和环行器进入光纤耦合器,与本振光相干拍频。最后,拍频信号由光电平衡探测器(balance detector,BD)转换为光电流,实现后续的信号处理和风场反演。定义信号光与本振光在拍频过程中振幅和相位的匹配程度为相干效率。该指标直接影响相干测风激光雷达系统的信噪比,是重要性能指标。由于光学系统涉及的参量较多,包括本振光束腰、光纤耦合器芯径、光学系统像差等,所以对相干效率的影响需要逐一分析。

图1 光学系统图

2 光学参量分析

2.1 本振光束腰

本振光通过窄线宽半导体种子激光器分束获得,光场ELO满足高斯分布：

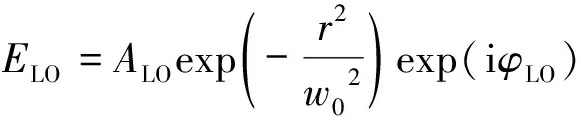
(1)

式中,ALO为本振光振幅强度,r为径向尺寸,w0为束腰半径,φLO为本振光初始相位。

回波信号光经光学系统耦合进入光纤耦合器,光场Es满足艾里分布：

(2)

式中,As为信号光振幅强度,J1(·)为第1类1阶贝塞尔函数,d为光学系统入瞳直径,λs为信号光波长,f为光学系统焦距,ks为信号光波数,φs为信号光初始相位,F为光学系统F数(F=f/d)。

通过计算本振光和信号光在光纤耦合器端面的叠加场,得到相干效率η：

η=

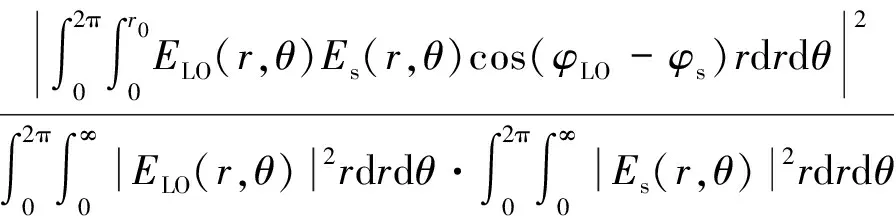
(3)

式中,r0为纤芯半径,r、θ为极坐标参数。

系统工作波长为1550 nm,光学系统焦距为300 mm,接收光纤芯径为10 μm,假设初始状态下信号光与本振光同相位,不同光瞳口径下相干效率与本振光束腰半径的变化曲线如图2所示。对于相同的光瞳口径,相干效率随光纤端面本振光的增大而先增大再减小,具有最大值,最大相干效率为81.4%。光瞳口径从80 mm增大到100 mm时,最优束腰半径从

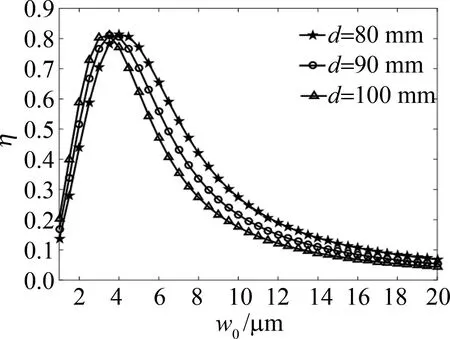
图2 相干效率与本振光束腰半径的变化曲线

4.25 μm减小到3.3 μm,这是因为在系统焦距一定的情况下,光瞳口径越大,信号光在焦平面处的艾里斑半径越小,所以最佳匹配的本振光束腰半径越小。束腰半径大于最优值时,相干效率急剧下降,当w0=20 μm时,相干效率只有6.8%,原因在于在束散角相同的条件下,束腰越大,光束质量越差,本振光光场振幅分布严重变形,有效相干面积大幅减小。

2.2 光纤耦合器芯径

本振光和信号光叠加后的光场与光纤耦合器的模场匹配时,才能近似空间信号光被全部无损接收,因此光纤耦合器端面有效叠加场的相干效率η′：

η′=

(4)

式中,M(r,θ)为光纤模场分布。光纤耦合器通常采用单模光纤,模场分布为：

(5)

式中,wm为模场半径。根据Marcuse经验公式,wm=r0/(lnν)0.5(2<ν<2.4),ν为归一化频率。

目前市场上传输光纤的芯径一般为8.4 μm～10.2 μm,也有特殊的4 μm、6 μm、12 μm和25 μm。不同光学F数情况下,相干效率与光纤耦合器芯径的变化曲线如图3所示。对于相同的光学系统,相干效率随光纤芯径的增大而迅速增大,然后趋于平稳。这是因为当耦合器芯径小于有效叠加场尺寸时,随着耦合器芯径的增大,接收视场将会增大,有效相干面积呈芯径的平方增大;当耦合器芯径大于有效叠加场尺寸时,即使耦合器芯径继续增大,但有效相干面积已不变,所以相干效率也保持稳定。不同光学系统的最大

图3 相干效率与光纤耦合器芯径的变化曲线

相干效率一致,为81.4%,但达到最大相干效率需要的最小芯径r0,min有差异。当F=2时,r0,min=4.5 μm,该类光纤耦合器属于常规货架产品;当F=4时,r0,min=6 μm,该类光纤耦合器需要定制。因此,光学系统的设计在满足最大相干效率前提下,需要权衡系统尺寸重量和光纤耦合器的选型及价格等因素。

2.3 光学系统像差

相位匹配是实现相干探测系统高效拍频的关键因素,光学系统像差会造成信号光波前畸变,产生相位误差,导致耦合光斑的斯特列尔比下降。利用Zernike多项式表征信号光波前畸变,光学系统产生的5种初级像差(倾斜、离焦、球差、彗差、像散)分别表示为[20]：

(6)

式中,W111、W020、W040、W131、W222分别为5种像差系数。

含有光学系统像差影响的相干效率η′表示为：

η′=

(7)

式中,信号光波数ks=2π/λs。

光纤耦合器纤芯直径为10 μm,天线口径为100 mm,本振光束腰半径为3.3 μm,相干效率与光学系统像差的变化曲线如图4所示。倾斜对相干效率的影响最大,当波像差为0.2λ(λ为工作波长)时,相干效率为71.8%,下降了9.6%,原因在于波前倾斜造成焦平面处信号光光斑偏移,与本振光同轴度降低,两光场重叠面积快速减小,损耗了有用的光能量。同等波

图4 相干效率与光学系统像差的变化曲线

像差,像散和离焦导致相干效率下降4.4%和2.1%,而彗差和球差造成的影响近似相等且最小,约0.3%。实际应用中,环境温度变化和机械振动必然存在,所以应采用主动或被动消热差设计,使整个光学系统波像差均方根值(root mean square,RMS)不大于0.06λ,同时对光学系统进行减震设计。

3 大气湍流的影响

相干测风激光雷达以大气为传输通道,由于大气湍流的存在,回波信号光会引入波前相位差[19]。根据冯卡曼模型,平均相位延迟〈φ2〉表示为[20]：

〈φ2〉=0.782Lks2Cn2L05/3

(8)

式中,L为探测距离,Cn2为大气折射率结构常数,L05/3为湍流外尺度。

考虑大气湍流影响后,相干效率η′表示为：

η′=

(9)

通常认为Cn2<10-17m-2/3为弱湍流, 10-17m-2/3≤Cn2≤10-15m-2/3为中湍流,Cn2>10-15m-2/3为强湍流。不同湍流强度情况下,相干效率与探测距离的变化曲线如图5所示。在相同天气条件下,相干效率随探测距离的增大而减小。对于强湍流情形,当L=8 km时,η′降至28.2%,再往远距离探测较困难;对于弱湍流情形,当L=30 km时,η′仍有41.6%,与目前报道的可实现探测最远距离相吻合。在同一探测距离处,随着湍流强度增大,相干效率减小,但减小量在不同距离区间有差异。当L<3 km时,|Δη′|<12.2%;当3 km≤L≤30 km时,η′急剧下降,特别地,在L=17 km处,减小量为最大值,|Δη′|max=48.1%。这是因为近距离探测时,大气散射回波信号强度较强,湍流影响较小;中远距离探测时,激光受大气扰动及退偏影响严重,散斑效应显著。

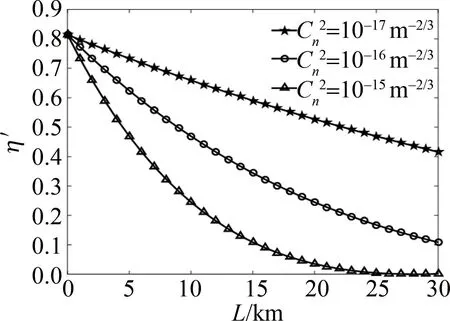
图5 相干效率与探测距离的变化曲线

4 实验与讨论

分束器本振光支路分别采用不同芯径的单模光纤跳线模拟本振光束腰w0,利用不同光瞳口径d的光学天线在同一测试地点,对相同环境的径向风速进行测量,如图6所示。由于测风激光雷达相干效率表征信号光场与本振光场的匹配度,所以最终由系统获得的信号频谱强度I或信噪比α量化表示。

图6 实验系统示意图

实验中,激光器工作波长为1550 nm,输出单脉冲能量为300 μJ,AOM中频为80 MHz,距离门长度设置为80 m。测量并记录不同天线口径下,不同本振光束腰拍频计算得到的第40个距离门的频谱强度,如表1所示。当天线口径为80 mm时,随着本振光的增大,频谱强度先增大后减小,因此本振光束腰半径存在最优解;随着天线口径增大,最优解会减小,与仿真结果相符。

表1 不同天线口径、不同本振光束腰下的频谱强度

为了验证接收光纤芯径对相干效率的影响,订制了纤芯直径D为12 μm和25 μm的光纤耦合器,与常用的9 μm芯径光纤耦合器进行比对实验。光学系统焦距为300 mm,口径80 mm和100 mm天线对应的F数分别为3.75和3,测量结果如表2所示。当光学F数不变时,频谱强度随光纤芯径的增大而增大,然后趋于平稳。在平稳状态前,对于相同的光纤芯径,F数越小,频谱强度越大。例如,对于9 μm光纤芯径,F数从3增加到3.75时,频谱强度下降25%。这是因为F数与光学口径成反比,大口径光学天线接收的回波信号更多。

表2 不同光学F数、不同接收光纤芯径下的频谱强度

为了验证光学系统像差对相干效率的影响,加工了两套相同的光学系统,一套经过严格装调测试,满足波像差RMS为0.036λ,如图7所示。另一套未做装调,并处于离焦状态,RMS远大于0.06λ。将两套光学系统装入测风激光雷达系统进行比对测量,记录在第40个距离门的频谱强度,前者为3×1011a.u.,信号细锐清晰,后者为2.5×107a.u.,尖峰噪声激增,信号完全淹没在噪声中。实验结果表明,满足光学像差要求的系统在第40个距离门处的中频信号频谱可有效提取,相干效率高;反之,信噪比极低,相干效率很低,与仿真结果一致。

图7 光学系统波前质量示意图

开展大气湍流影响实验时,将雷达安置于同一测试地点,针对典型天气条件(条件一：大雨或雾霾,能见度V≤5 km;条件二：晴朗,大气气溶胶含量高,能见度V≥20 km)进行测量,并利用系统在不同探测距离处的信噪比α表征相干效率,测量结果如图8所示。光学天线口径为100 mm,束散角为40 μrad,波像差为0.036λ,本振光束腰为3.3 μm,光纤耦合器芯径为12 μm。晴空条件下,系统最远测程可达15 km,大雨或雾霾天气条件下,系统最远测程6 km,原因在于雨水和大气微粒对信号光的吸收和散射导致光强起伏和相位波动,造成相干效率下降。对于近程,即L<3 km时,湍流对系统信噪比影响较小;当L>3 km时,在强湍流情况下,系统信噪比随探测距离的增加急剧下降;当L=6 km时,系统信噪比小于5,提取中频信号频谱变得困难。实验结果与仿真结果基本吻合,实测的最远测程比理论值小,且信噪比曲线存在局部波动,这是因为建模仿真使用的冯卡曼模型将相位噪声理想化为平均相位延迟,忽略了实际情况中大气湍流的随机性。

图8 信噪比与探测距离的变化曲线

5 结 论

针对相干测风激光雷达,阐述了光学系统组成和工作原理,定义了系统相干效率;基于本振光和信号光的光场叠加理论,讨论分析了本振光束腰、光纤耦合器芯径、光学系统像差对相干效率的影响;引入大气湍流平均相位延迟参量,建模分析了大气扰动对相干效率的影响,并开展了验证实验,测量了不同光学参量的系统在典型天气条件下的信噪比。结果表明,光瞳口径从80 mm增大到100 mm时,最优束腰半径从4.25 μm减小到3.3 μm。当光学F数不变时,相干效率随接收光纤芯径的增大而增大,最后趋于平稳。对于9 μm光纤芯径,F数从3增大到3.75时,频谱强度下降25%。为保证系统相干效率,光学系统波像差RMS不大于0.06λ。在相同天气条件下,相干效率随探测距离的增大而减小,晴朗天气条件下,能见度不小于20 km时,系统最远测程可达15 km。对于近程,湍流对相干效率的影响较小,当L>3 km时,在强湍流情况下,系统信噪比随探测距离的增加急剧下降;当L=6 km时,系统信噪比小于5。因为大气干扰和退偏效应客观存在,所以在优化光学参量的同时,应考虑信号光与本振光的偏振匹配。

本文中对相干测风激光雷达激光器和光学天线的设计,以及接收器件的选型和参数优化具有参考意义。