基于优化遗传算法的焊接机器人路径规划研究

范祺，蔡玉强*,，贾思楠

基于优化遗传算法的焊接机器人路径规划研究

范祺1，蔡玉强*,1，贾思楠2

（1.华北理工大学 机械工程学院，河北 唐山 063210；2.华北理工大学 矿业工程学院，河北 唐山 063210）

为提高焊接机器人的精度和效率，得到最优的机器人路径规划，以现代HA006型机器人为研究对象，在SolidWorks平台构建其三维模型，依据D-H法获得其连杆参数数据，进行运动学正逆解理论计算，使用MATLAB robotics工具箱进行运动学正逆解验证；使用五次多项式曲线方法进行关节空间轨迹规划，发现加速度在开始结束位置的突变是影响运动过程平稳性的主要原因；基于优化遗传算法进行路径规划，将适应度函数结合路径长度和平滑度两项指标，最终仿真得到平滑的优化路径曲线。

D-H法；运动学正逆解；五次多项式；优化遗传算法；路径规划

随着金属加工需求的增加，对焊接工艺的要求变得越来越高，在生产线中引入焊接机器人是大势所趋。焊接机器人相比于传统手工焊大幅提高了焊接精度。目前常见的焊接机器人都是在机器人末端执行器处安置焊枪，机器人末端位姿运动能否达到预期运动规律，直接决定了焊接精度与焊接效率[1]。合理的机器人轨迹规划和路径规划是提高作业质量的关键[2]。

1 机器人运动学

1.1 机器人连杆参数

选取HA006型机器人为研究对象，在SolidWorks平台构建其三维模型，如图1所示。

图1 HA006机器人三维模型

采用Denvait和Hartenberg提出的在空间中表达机器人各构件相对于坐标系的矩阵表述方法，简称D-H法[3]。根据D-H法，HA006型机器人连杆参数坐标系如表1所示。

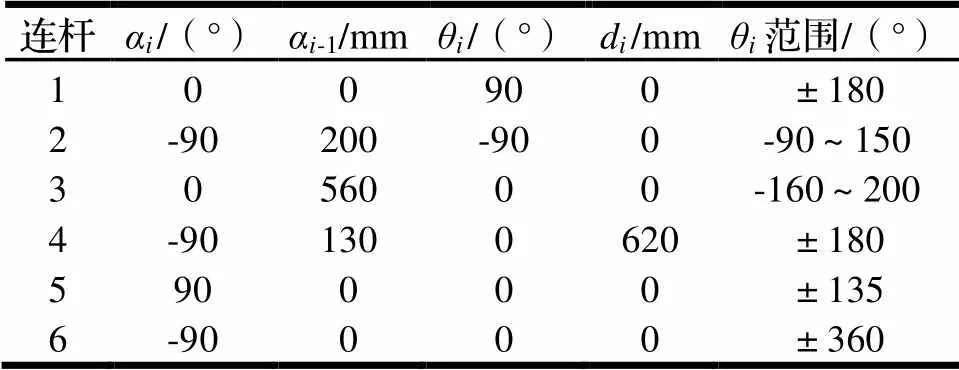
表1 HA006机器人D-H参数

注：α为连杆扭转角；α-1为连杆长度；θ为关节转角；d为连杆偏距。

1.2 MATLAB中建立机器人模型

在MATLAB robotics工具箱中根据D-H参数建立空间连杆模型，调用MATLAB中link类函数建立机器人模型，如图2所示。

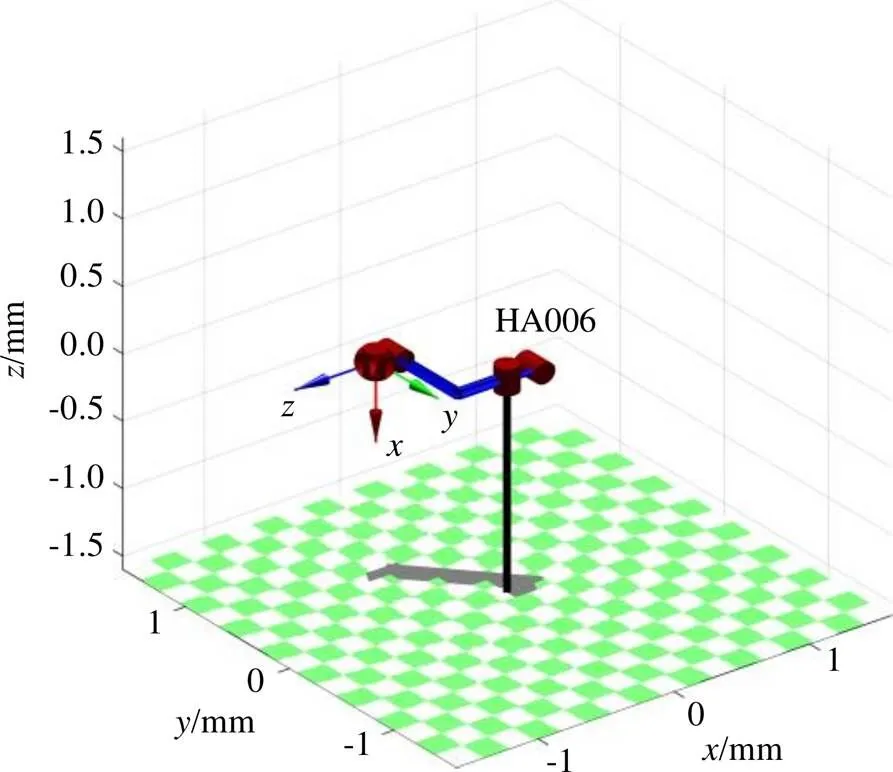
图2 MATLAB robotics工具箱模型

建立模型的程序为：

L(1)=Link([000pi/20],'modified');

L(2)=Link([-pi/20.200-pi/200],'modified');

L(3)=Link([00.560000],'modified');

L(4)=Link([-pi/20.13000.6200],'modified');

L(5)=Link([pi/20000],'modified');

L(6)=Link([-pi/20000],'modified');

Six_Link=SerialLink([L(1),L(2),L(3),L(4),L(5),L(6)]);

Six_Link.name='HA006';

1.3 正运动学

机器人运动学正解就是将各连杆相对于基坐标系变换矩阵做相乘变换，在已知各关节运动角度的基础上，得到末端执行器的位姿矩阵为[4]：

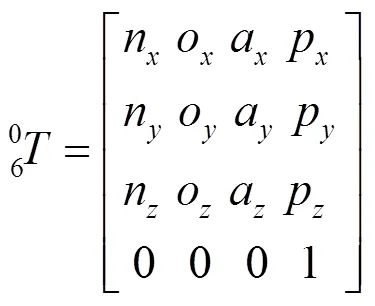
式中：

在MATLAB中调用fkine函数进行运动学正解验证，选取关节角度值依次为pi/2、pi/3、pi/4、pi/2、pi/6、pi/2，按照理论推导出的末端执行器的位姿矩阵为：

调用的fkine函数为：

Six_Link.fkine([pi/2pi/3pi/4pi/2pi/6pi/2])

最终验证仿真结果与计算理论值一致。

1.4 逆运动学

运动学逆解是在已知机器人末端姿态矩阵的情况下反求出各关节角的大小，用代数方法反求出各关节角的角度大小为：

将式（2）代入调用的ikine[5]中进行运动学逆解验证，调用的ikine函数为：

Six_Link.ikine6s(T1)

计算结果显示运动学逆解与理论值一致，说明机器人连杆参数模型的正确性，机器人模型建立无误，可以进行轨迹规划等后续操作。

2 机器人关节空间轨迹规划

关节空间轨迹规划中常用的方法是三次、五次以及高次插值多项式的方法，为了提高轨迹的平滑性能，未来主流的方法是B样条曲线、NURBS曲线方法。五次插值多项式方法通常是已知初始位置与结束位置的角度和角速度，增加了加速度的约束条件，适用于点到点之间的运动，利用MATLAB软件调用jtraj函数进行仿真[6-8]，可以得到各关节运动参数随时间变化的关系，其中关节6的角度、角速度、角加速随时间的变化情况如图3所示。

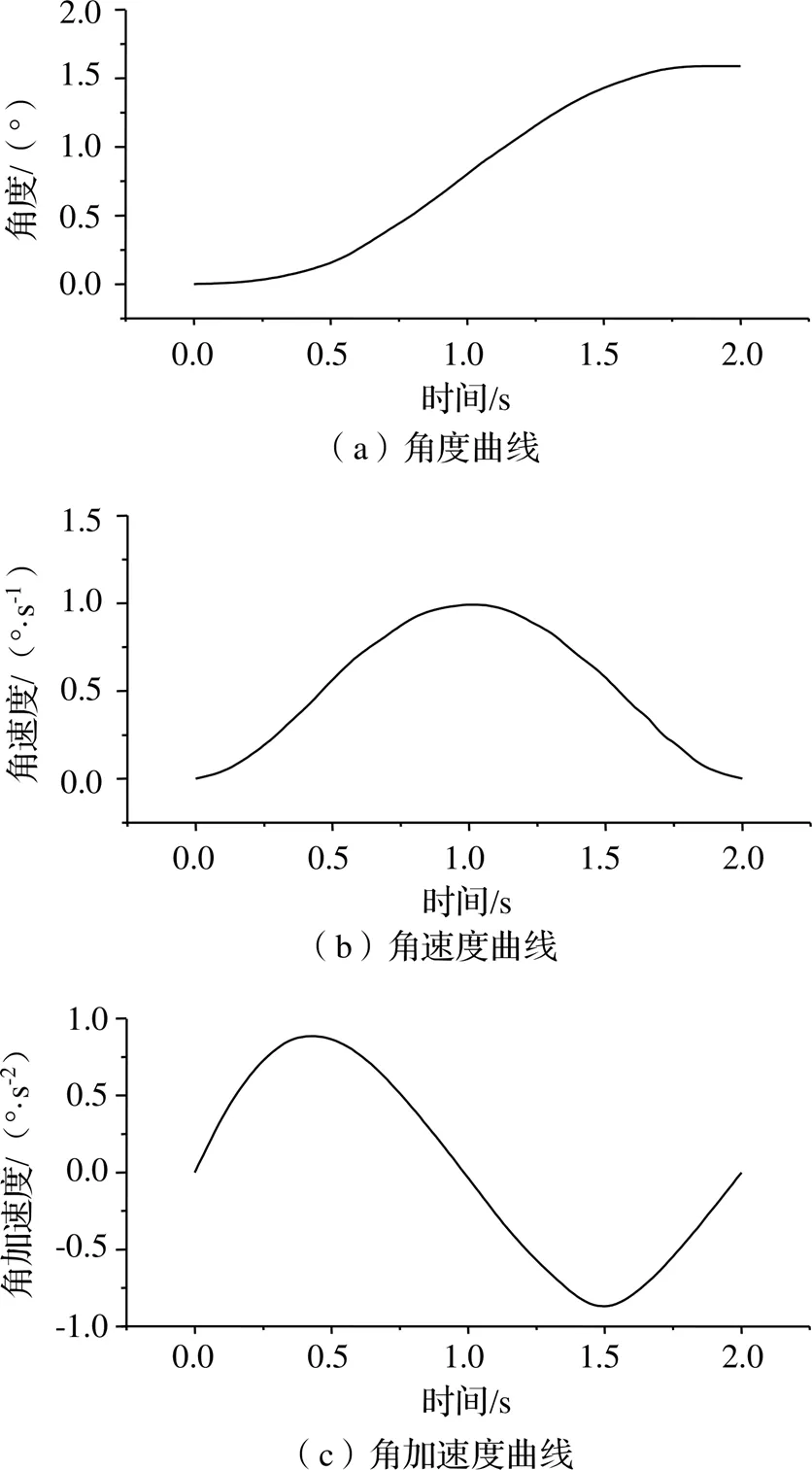
图3 关节参数运动曲线

在图3运动轨迹中，关节6的角度、角速度、角加速随时间变化的曲线是连续但不够平滑，特别是在开始、结束和曲线拐点时刻，加速度的突变是机器人运动过程中产生冲击的主要原因。

3 基于优化遗传算法的机器人路径规划

在当前的机器人路径规划领域中，包含Dijkstra、A*、RRT（Rapidly-exploring Random Tree，快速随机探索树）、RRT*和InformdRRT*算法，以及遗传算法和蚁群算法。其中基于智能算法的遗传算法和蚁群算法具有完备性，只要在起始点与目标点有解，那么就一定能够得到解，如果无解说明路径不存在[9]。各类算法中，优化遗传算法的计算时间最长、效率最低，但规划的路径更为平顺，路径长度更为合理。各类算法的计算原则如图4所示。

遗传算法在串联机器人路径规划中应用较为广泛，算法的规划流程如图5所示。

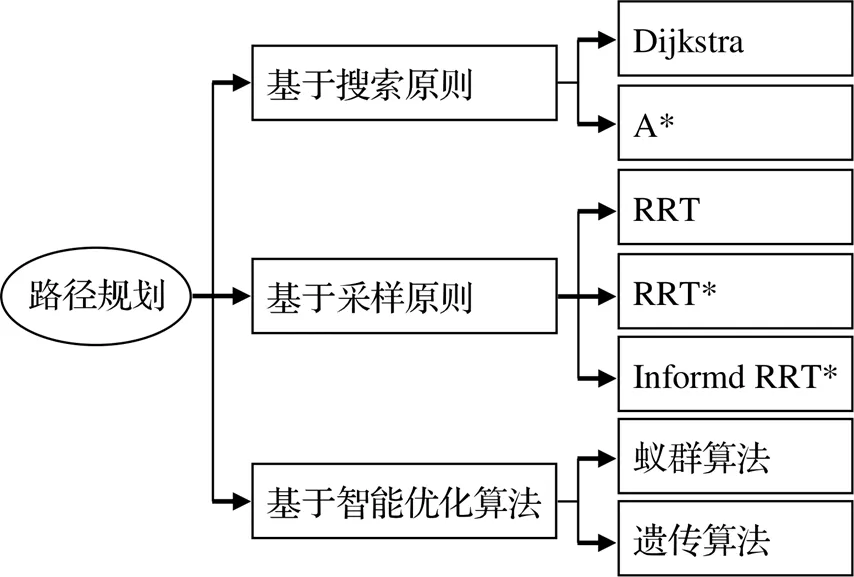
图4 路径规划算法

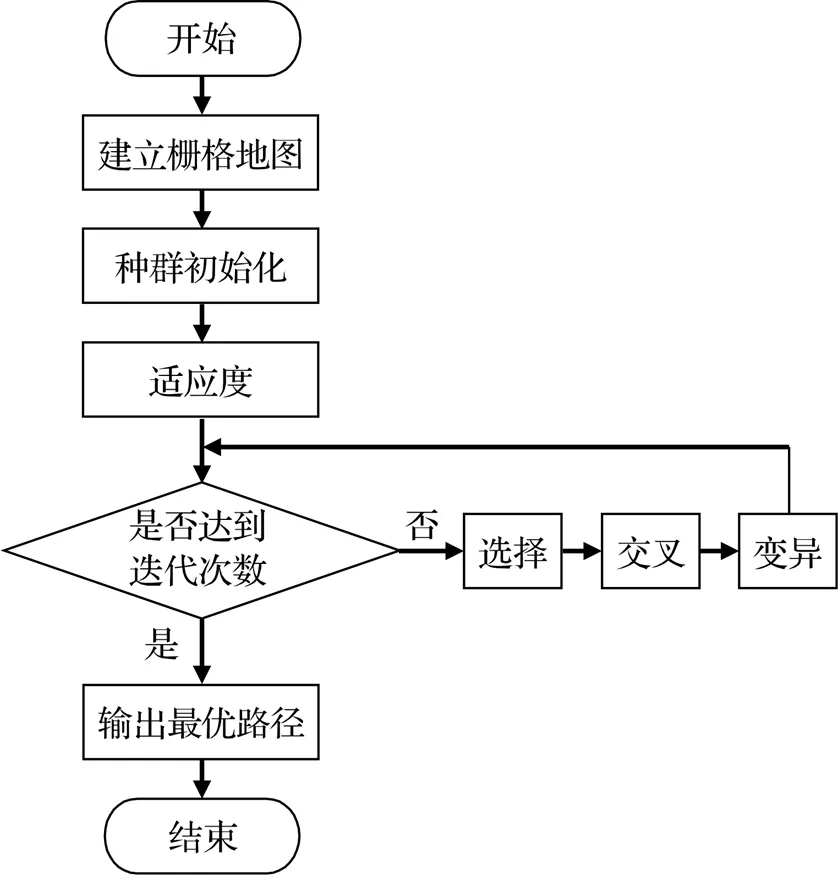
图5 遗传算法流程图

3.1 建立栅格地图

通过栅格法建立机器人工作的静态环境模型，空间环境精度与栅格面积成反比，栅格面积越小，存储的信息量就越大，这样路径规划所需的时间就越长；栅格面积如果过大，工作空间环境信息[9]又不能准确地表达出来，因此选择了20×20的栅格地图，并做出以下规定；

（1）路径规划中把机器人当做质点处理；

（2）机器人运动空间为二维平面，忽略掉障碍物高度；

（3）在机器人开始运动后，确定障碍物大小，且不存在动态障碍物。

为方便仿真，机器人整体运动空间用正方形栅格地图表示，如图6所示，栅格黑色表示栅格内存在障碍物，白色表示栅格内无障碍物。

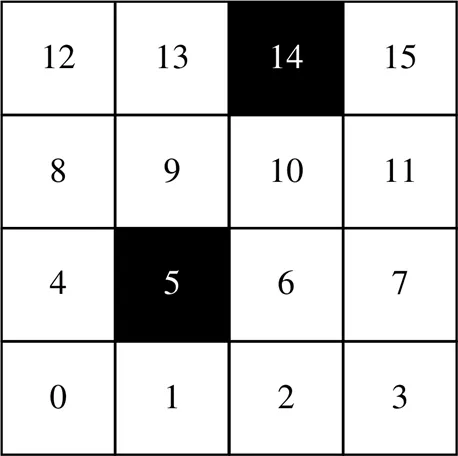
图6 栅格地图

在构建运动栅格地图时，建立直角坐标系，原点为左下角第一个栅格，在坐标系内用(,)的形式表示每一个栅格，从原点开始对栅格进行编号，编号和坐标间的关系为：

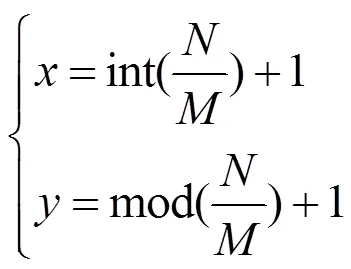
式中：为栅格号；为栅格数量；mod为取余；int为取整操作，表示取整格尺为每一行栅格数。

3.2 种群初始化

机器人的起始位置为栅格0，目标位置为栅格399。种群初始化要求随机产生多条不与障碍物相撞的可行路径，机器人每次行走一个栅格，因此每行每列至少有一个栅格在可行路径中。所以初始化时先按顺序在每一行随机取出一个无障碍栅格，形成一条间断的路径，再从第一个栅格开始判断相邻的两个栅格是否为连续栅格，栅格是否连续的判断方法为：

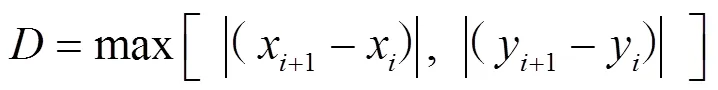
若＝1，则说明两个相邻栅格连续，可在避免死循环的情况下继续规划路径。

对于≠1的不连续栅格，需取中点栅格，其坐标为：

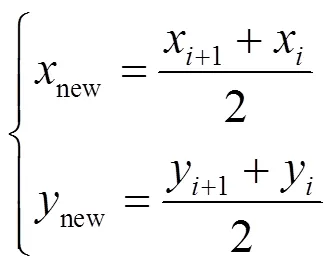
若新栅格为无障碍物栅格，则插入两个不连续栅格中间。继续判断新插入是否连续，若不连续则循环以上步骤，直到两个栅格连续。当两个栅格连续后取下一个栅格，循环以上步骤，直到整条路径连续。

3.3 适应度函数计算

传统遗传算法中，遗传因素中主要是路径因素，要保持路径最短。改进遗传算法中，适应度函数包括最优路径和平滑度两部分，路径长度为：

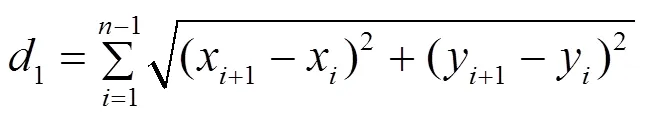
路径长度的适应度为：

路径规划中需尽可能避免过多次的大幅度转弯，因此需要控制路径轨迹的平滑度，定义平滑度为路径中所有相邻三点的距离，平滑度适应度为2。

适应度函数的两部分需要取一个权重，为：

＝1＋2（9）

式中：和为适应度函数的权重参数，决定了路径的最终走向。

3.4 遗传算子

选择轮盘赌方法，先获得适应度函数各部分之和，根据权重占比情况，选择出下一代个体。这种方法在保证了部分非最优的个体的同时，又防止陷入局部最优解的问题。

交叉前先确定交叉概率p，之后产生随机数与p比较，进行交叉操作的条件是随机数小于p。交叉操作是在已获得的两条路径中找出两个相同栅格，选取其中一个栅格交换它们之后的路径。

变异前先确定变异概率p，之后产生随机数与p比较，进行变异操作的条件是随机数小于p。在随机路径中找到除起点终点外的两个栅格，去除它们之间的路径，然后以这两个栅格为相邻点，按照初始化操作将这两个栅格连续化。这样的变异操作增加了个体的多样性[10]。

3.5 仿真结果

使用MATLAB遗传算法工具箱进行仿真，设定种群数量为150，p＝0.8，p＝0.2，＝8，＝2，限制迭代次数不超过100次，仿真后得到图7。

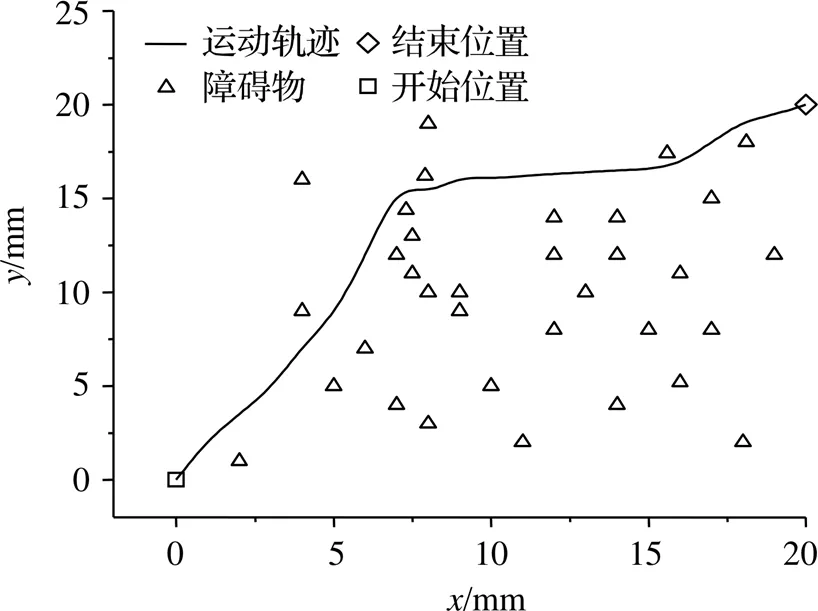
图7 路径仿真结果

由仿真结果可看出，结合考虑了路径长度和平滑度的路径规划，在经过多次迭代后达到收敛，最终规划的路径在长度上虽然不是最短的，但曲线的平滑性得到较大改善，避免了锐角的出现。

4 结论

（1）以HA006型机器人为研究对象，得到其连杆参数数据，通过理论计算得到其运动学正逆解，在MATLAB的robotics工具箱中进行正逆解验证，最终证明HA006机器人模型建立的正确性。

（2）机器人关节空间轨迹规划利用五次插值多项式方法，得到其关键运动参数随时间变化的曲线，发现加速度突变问题是影响运动过程平稳性的关键，为后续提高机器人平稳性、减少振动等技术要求做了准备。

（3）为实现基于优化遗传算法的路径规划，介绍了种群初始化、适应度函数、选择方法、变异方法和交叉方法，针对适应度函数进行优化，解决传统遗传算法路径不够平滑的问题，设计更加合理的平滑函数，得到合理的路径规划。

[1]孙英飞. 我国工业机器人发展研究[J]. 科学技术与工程，2012，12（12）：2912-2920.

[2]戴为志，俞海涛，王继文. 钢结构焊接机器人的现状及发展方向[J]. 金属加工（热加工），2021（12）：7-12.

[3]任军辉，乔琳. 基于UG机器人末端执行器的设计与运动仿真[J]. 南方农机，2022，53（5）：22-24.

[4]杨晓玉，富荣昌，王文远. 基于ADAMS和MATLAB的双足机器人运动轨迹规划和控制的联合仿真[J]. 煤矿机械，2022，43（1）：6-9.

[5]庄衡衡，丁飞，章华涛，等. 五自由度机器人运动控制与空间位姿仿真系统[J]. 中国测试，2021，47（11）：14-20.

[6]李双双. 工业机器人建模、运动仿真与轨迹优化[D]. 呼和浩特：内蒙古大学，2012：30-34.

[7]于佳乔，李岩. 基于改进遗传算法的自动导航小车路径规划调度[J]. 机床与液压，2022，50（5）：16-20.

[8]乐英，库巍，卢艺，等. 基于优化的六自由度工业机器人NURBS轨迹规划[J]. 组合机床与自动化加工技术，2017（11）：41-43.

[9]曾关平，王直杰. 基于改进遗传算法的机械臂时间最优轨迹规划[J]. 科技创新与应用，2020（22）：6-9.

[10]胡锦楠，杨泽. 基于遗传算法的喷涂轨迹规划方案研究[J]. 科技创新导报，2019，16（25）：68-69.

Path Planning of Welding Robot Based on Optimized Genetic Algorithm

FAN Qi1，CAI Yuqiang1，JIA Sinan2

( 1.School of Mechanical Engineering, North China University of Science and Technology, Tangshan 063210, China; 2.School of Mining Engineering, North China University of Science and Technology, Tangshan 063210, China)

In order to improve the welding accuracy and efficiency of the welding robot and obtain the optimal path planning, a three-dimensional model of Hyundai Robot HA006 is constructed on the SolidWorks platform. The connecting rod parameter data is obtained based on the D-H method, and the theoretical calculation of kinematic forward and inverse solution is carried out. The kinematic forward and inverse solution is verified by using the MATLAB robotics toolbox, and the joint space trajectory planning is carried out by using the combination of quintic polynomials andspline curves. It is found that the sudden change of acceleration at the beginning and end position is the main reason that affects the stability of the motion process. Based on the optimized genetic algorithm and combined the adaptability function with the two indicators of path length and smoothness, the smooth optimized path curve is finally obtained by simulation.

D-H method；kinematic forward and inverse solution；quintic polynomial；optimized genetic algorithm；path planning

TP242.3

A

10.3969/j.issn.1006-0316.2023.01.011

1006-0316 (2023) 01-0068-06

2022-03-03

河北省教育厅项目（2019GJJG216）；华北理工大学博士启动基金项目（BS2017094）

范祺（1998－），男，河北唐山人，硕士研究生，主要研究方向为机械机构学与机械动力学，E-mail：tangshanfankuli@163.com。*通讯作者：蔡玉强（1967－），男，河北唐山人，博士，教授，主要研究方向机械动力学，E-mail：1824880027@qq.com。