基于刚柔耦合动力学的高速列车转向架构架振动疲劳研究

李传迎，李鹏，吴兴文，董晓华

基于刚柔耦合动力学的高速列车转向架构架振动疲劳研究

李传迎1，李鹏1，吴兴文*,2，董晓华3

（1.中车青岛四方机车车辆股份有限公司，山东 青岛 266111；2.西南交通大学 机械工程学院，四川 成都 610031；3.西南交通大学 牵引动力国家重点实验室，四川 成都 610031）

构建了考虑转向架构架高频柔性的刚柔耦合动力学模型，结合模态应力恢复方法实现了考虑轨道激励的转向架构架动应力求解。基于该模型，提出一种基于典型服役模式扫频激励的转向架构架动态薄弱位置识别方法，研究了转向架构架薄弱位置动应力在典型服役工况下的应力特征和各特征工况损伤；最后，结合京广线路分布特征，研究了转向架构架薄弱位置的损伤。结果表明：基于典型服役模式扫频激励识别的结构动态薄弱位置，能够包含传统准静态方法识别的静态薄弱位置，同时可以识别薄弱位置的敏感频带；曲线半径对转向架关键位置损伤具有显著影响，随着曲线半径的减小损伤显著增大；考虑京广线曲线和直线分布特征，计算得到的转向架构架关键位置损伤满足1200万公里设计寿命的要求。

高速列车刚柔耦合动力学；模态应力恢复；静态薄弱位置；动态薄弱位置

高速动车组转向架构架在实际运营过程中既要承受来自车体的低频载荷，又要承受来自轮轨的高频载荷。针对转向架构架强度和疲劳强度，传统方法主要参照EN13749[1]、UIC[2]和JIS[3]等标准，使用准静态方法进行校核。该方法一般只能模拟车体自上而下的低频载荷，低估了实际服役过程中轮轨高频载荷对转向架构架的影响，难以识别构架结构模态振动对薄弱位置的贡献[4]，从而使得转向架部件，特别是转向架的附属部件，在实际服役过程中容易遭受轮轨高频振动导致的结构振动疲劳问题。

任尊松等[5]通过有限单元法和动力学理论建立了完整的刚柔耦合动力学模型，并通过模态应力恢复法得到了柔性构架的动态应力响应，为振动疲劳寿命的评估奠定了基础。卢耀辉等[6]通过对仅考虑构架主体柔性的刚柔耦合动力学模型与刚体动力学模型进行对比，发现柔性构架垂向加速度响应远大于刚性构架；而且随着频率的增大，由于构架自身结构弹性振动，柔性构架对响应的影响突出，刚性构架对响应的影响则趋于衰减；最后利用多项式拟合法和Miner线性累计损伤理论对构架的裂纹扩展寿命进行了计算。王蕾等[7]利用准静态方法对构架进行静强度计算，并确定构架静态薄弱位置，其次利用SIMPACK动力学模型和快速傅里叶变换得到加速度功率谱，最后利用模态叠加法、Steinberg三区间法和累计损伤理论对焊缝位置的疲劳强度进行寿命评估，发现与横向和纵向相比，由于构架垂向刚度小，垂向加速度激励对构架的损伤影响最大。朱涛等[8]首先利用傅里叶变换对时域数据与频域数据进行相互转换，然后利用三次样条插值法获得速度与加速度关于时间的函数，最后基于频域法对构架薄弱位置的疲劳寿命进行评估，发现在基于频域法进行寿命评估时，利用位移激励、速度激励或者加速度激励转化出的频域信号计算得到的构架寿命差别很小。张丽等[9]研究了考虑构架弹性振动响应与不考虑构架弹性振动响应对某车体构架疲劳寿命的影响，对比发现，考虑构架弹性振动后，测点累计损伤值更大，疲劳寿命只有原设计寿命的1/3，甚至更低，由此可见，构架弹性振动对构架的影响不可忽略。

实际服役条件下，构架弹性振动会引起构架薄弱位置的动态变化，称为动态薄弱位置[10]，而由准静态载荷产生的应力薄弱位置称为静态薄弱位置。动态薄弱位置与静态薄弱位置相辅相成，可以更加全面地掌握构架的薄弱位置，对构架的抗疲劳设计具有重要意义。

本文基于柔性体建模理论和模态应力恢复法，建立了考虑构架柔性的高速列车刚柔耦合动力学模型；依据UIC 615-4[2]，基于构架有限元模型，对构架进行静态薄弱位置识别；基于构架扫频模型，通过模拟浮沉、点头、侧滚和扭转四种工况，对构架进行动态薄弱位置识别。在此基础上，基于京广线路条件，研究分析不同曲线半径对构架特征应力谱的影响，最后基于Miner线性累计损伤理论和材料-曲线对构架薄弱位置进行寿命评估。

1 基于模态法的高速列车刚柔耦合动力学模型

高速列车构架在实际服役过程中，会受到来自车体自上而下的低频载荷和来自轮轨之间的高频激励载荷。轮轨高频激励载荷一般通过轮对轴箱和一系悬挂系统传递至构架，从而引发构架结构模态共振，最终导致构架疲劳失效。传统的多刚体动力学模型只能反映系统的低频特性，不能考虑构架弹性振动带来的影响。为此，本文从大系统刚柔耦合动力学的角度研究高速列车构架振动疲劳特性。首先基于有限元法建立高速列车构架有限元模型，构架有限元网格采用SOLID185实体单元，共划分675173个单元和215291个节点；然后基于模态综合法和高速列车动力学模型建立考虑构架柔性的高速列车刚柔耦合动力学模型，如图1所示。其中，钢轨外形采用CN60，车轮踏面外形采用LMA，模型中横向止挡、抗蛇行减振器的非线性特性均采用分段线性方式来描述。

图1 高速列车刚柔耦合系统动力学模型

相对于构架参考坐标系，有：

(,)＝＋(,) （1）

式中：为构架上任意点位置坐标；(,)为点弹性振动；(,)为点弹性振动响应。

根据模态叠加法，有：

(,)＝() （2）

式中：为模态矩阵；()为构架各阶模态正则坐标。

根据模态应力恢复法，有：

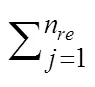
式中：为弹性振动导致的节点应力；n为模态应力恢复法中考虑的模态数目；σ为第阶模态应力；q为第阶模态坐标。

在本文的研究中，考虑了构架1000 Hz以内的柔性模态，构架前5阶模态如图2所示。

2 构架薄弱位置识别

大量研究表明，结构失效主要起始于结构的薄弱位置，因此如何准确又全面地识别构架薄弱位置是构架强度设计的关键。构架在准静态载荷作用下产生的应力薄弱位置称为静态薄弱位置；在实际服役过程中，由于动态激励（如钢轨波磨、车轮多边形等）引起构架高频弹性振动而导致构架产生应力集中的位置称为动态薄弱位置。为此首先基于UIC 615-4[2]利用以往的准静态分析方法对构架静态薄弱位置进行识别，然后利用考虑构架柔性的刚柔耦合动力学扫频模型，使用扫频方法模拟构架各种服役模式，以识别构架动态薄弱位置。

2.1 构架静态薄弱位置识别

为识别构架静态薄弱位置，基于UIC 615-4定义边界条件，并编制13个静强度组合工况，模拟高速列车在实际服役过程中经常承受的载荷，主要包括垂向载荷、横向载荷和轨道扭曲等。结果表明，基于UIC 615-4规定的各组工况下，构架最大等效应力为150.1 MPa，位置为转臂座拐角焊缝区域，小于构架材料焊缝区许用应力215 MPa，因此构架满足静强度要求。转向架构架薄弱位置区域主要如图3所示。

2.2 构架动态薄弱位置识别

基于准静态方法得到的静态薄弱位置，既不能完全反映构架关键薄弱点，又不能反映构架弹性共振对关键位置应力的贡献量，因此，有必要对高速列车在实际服役条件下的动态薄弱位置展开研究。

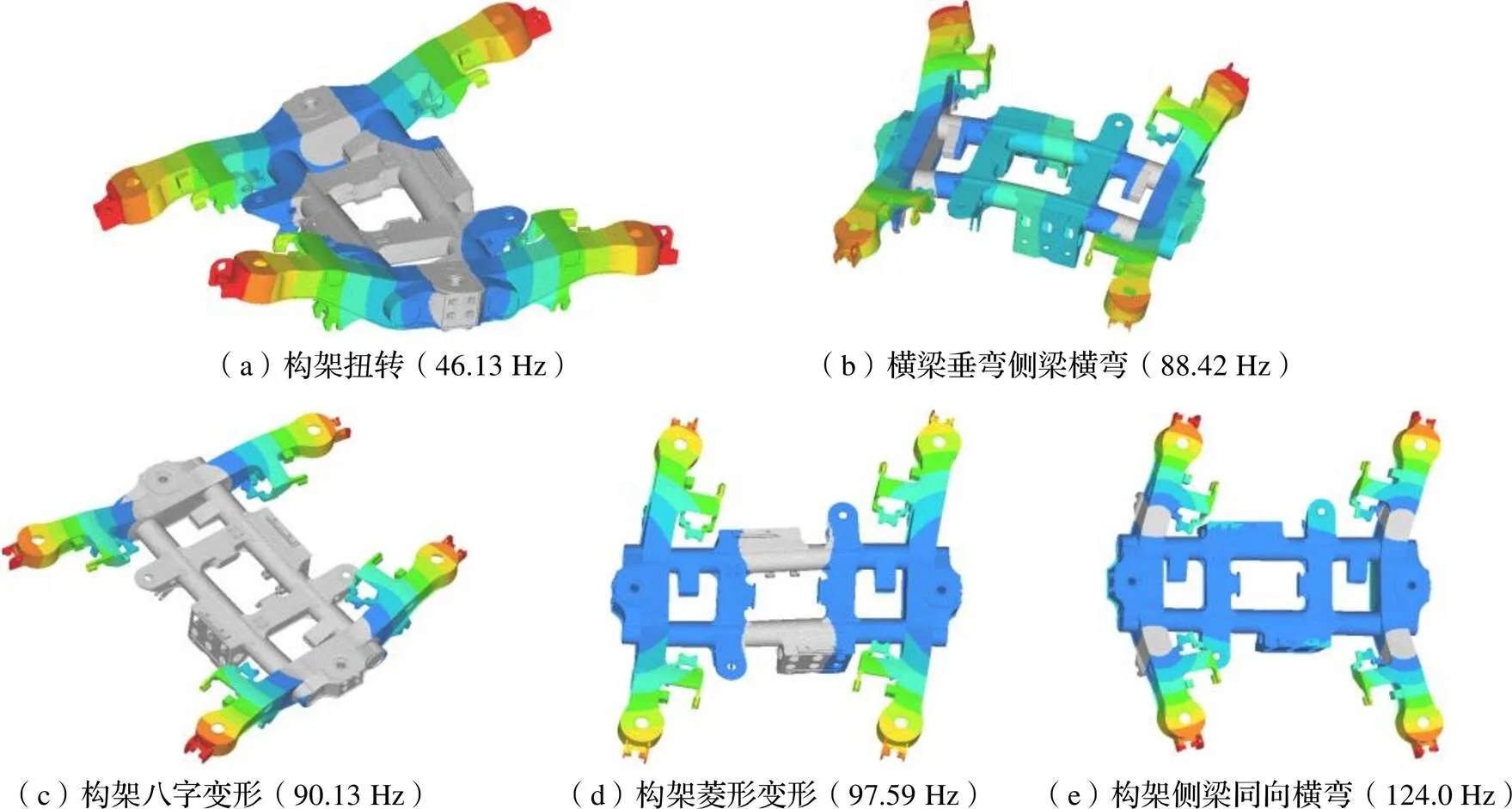
图2 构架振型及频率

图3 构架静态薄弱位置

利用考虑构架柔性的高速列车刚柔耦合动力学模型，结合模态应力恢复法，考虑线路中可能存在的激励频率，将其中的车轮及轨道删除，保留车轴。在轴箱位置处设立幅值为2 mm、频率从小变化到800 Hz的正弦扫频激励，仿真60 s，并设置正弦扫频激励的方向，可组合出构架沉浮、点头、侧滚及扭转等激励形式，从而得到能激起构架高频模态的扫频模型，以反映构架在实际服役过程中可能出现的振动情况，分析各种激励频率条件下构架的动态薄弱位置。具体扫频激励施加示意图如图4和表1所示。

表1 各种扫频激励模式

注：表示垂向向下，-表示垂向向上。

通过扫频分析，高速列车构架动态薄弱位置主要如图5所示。

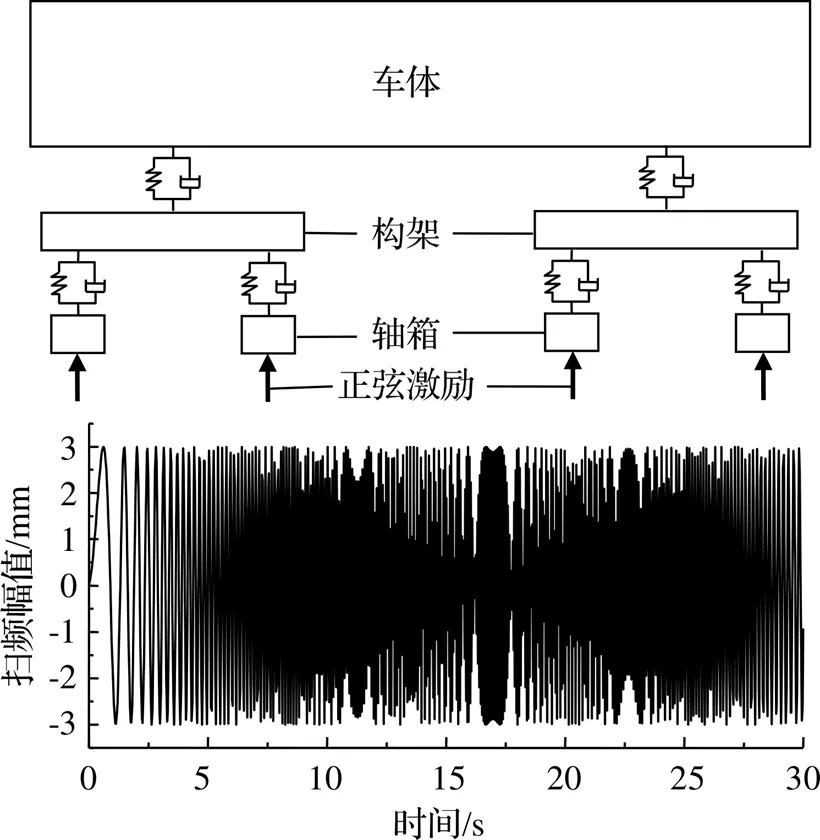
图4 扫频激励及其示意图

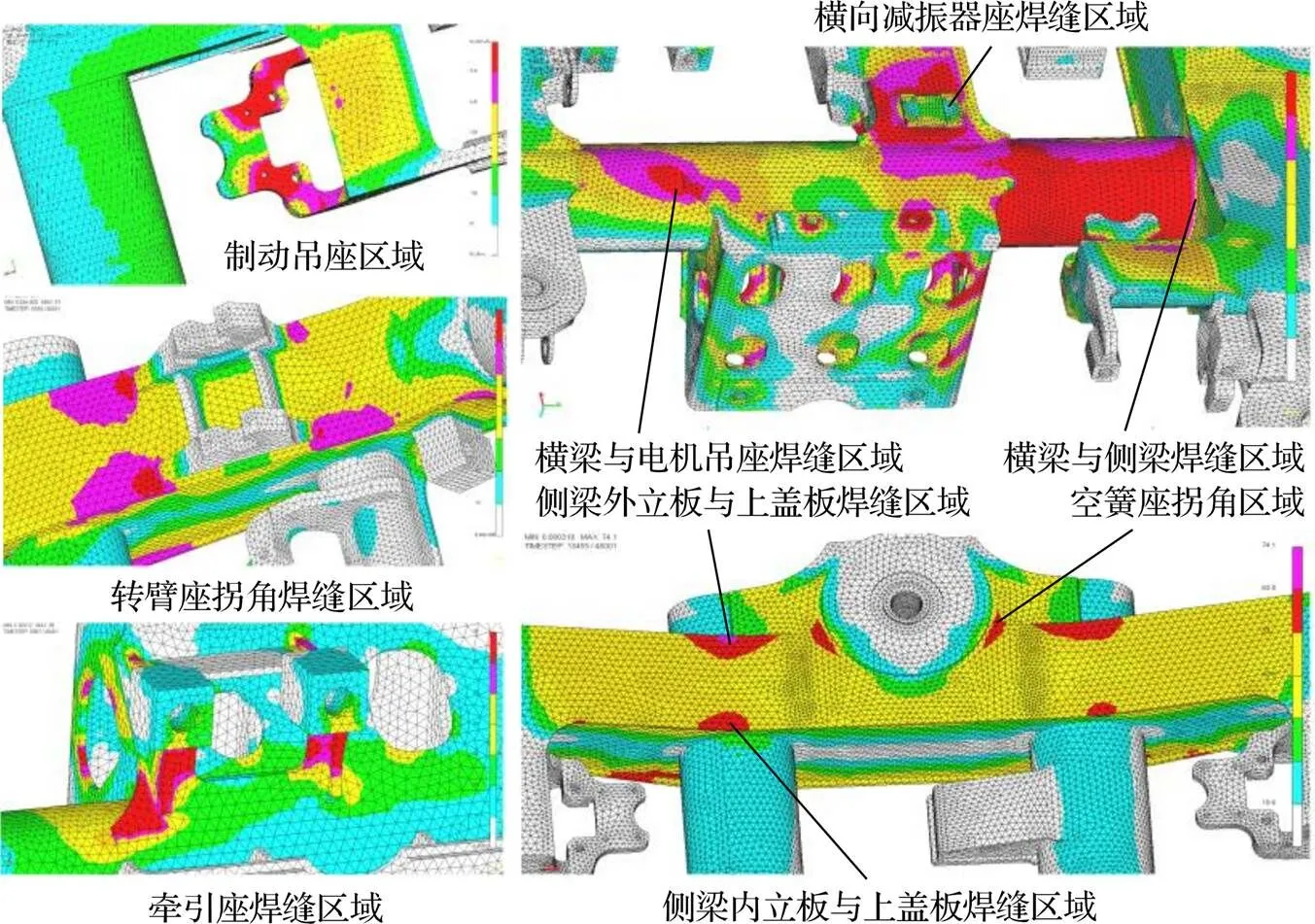
图5 构架动态薄弱位置

图6给出了浮沉扫频激励下构架几个关键位置的动应力频谱图。结果表明，关键薄弱位置在49 Hz、62.8 Hz、80 Hz、97 Hz、125 Hz和161.8 Hz附近出现明显的共振峰值。其中49 Hz与构架的扭转模态（46.13 Hz）发生共振；97 Hz与构架菱形变形模态（97.59 Hz）发生共振；125 Hz与构架侧梁同向横弯模态（124 Hz）发生共振；161.8 Hz与构架侧梁异向垂弯模态（168.3 Hz）发生共振，构架菱形变形模态对构架薄弱位置的影响较大。构架关键位置在共振区域应力数倍增大，是导致高速列车构架振动疲劳失效的主要原因，因此适当重新修改设计转向架构架结构，使转向架构架在实际服役过程中不再与构架自由模态发生共振，对高速列车安全运行具有重要意义。62.8 Hz和80 Hz初步推断为与转向架局部弹性振动模态发生共振，但仍不排除由钢轨波磨和车轮多边形导致。

对比构架静态薄弱位置可以发现，构架动态薄弱位置更加全面地反映了构架关键薄弱位置，而且根据构架自由模态和关键位置时频谱图，既可以分析共振区域，又可以直观分析构架弹性共振对关键位置应力的影响。

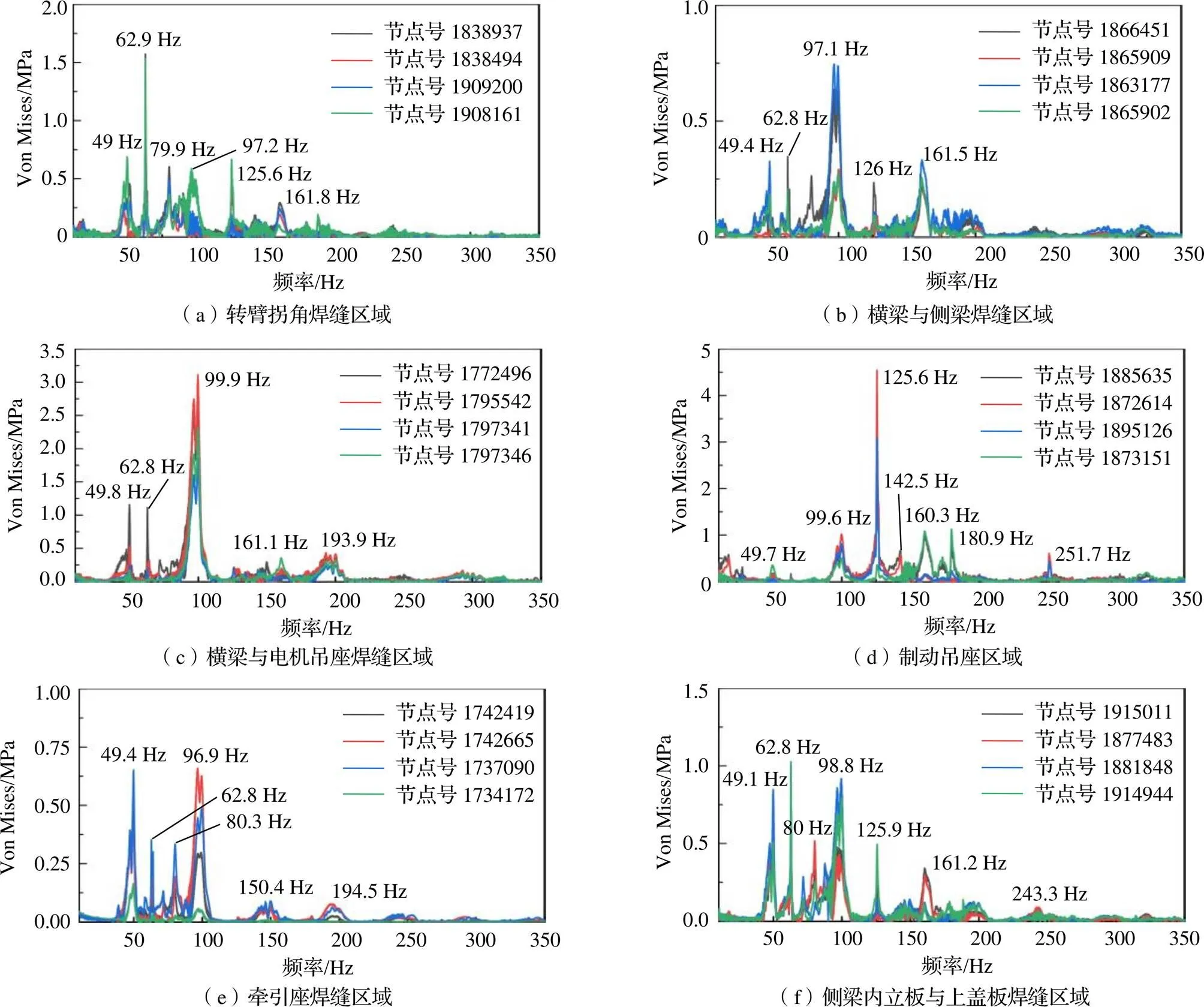
图6 浮沉激励模式下关键部位频域响应

3 构架薄弱位置动应力及损伤研究

高速列车转向架构架在实际服役条件下，主要受到线路几何和轨道不平顺导致的动态载荷。为明确线路曲线半径对构架关键薄弱位置应力的影响，本节基于京广线路条件、考虑构架柔性的刚柔耦合动力学模型，研究了同一速度下不同曲线半径对构架薄弱位置动应力的影响，并利用雨流技术法和国际焊接学会IIW标准的焊接接头-曲线（疲劳应力与疲劳寿命的关系曲线）对构架薄弱位置的寿命进行评估。

3.1 薄弱位置动应力分析

根据京广线路实际曲线比例和特点，取半径800 m、1200 m、2500 m、6000 m和14000 m（直线）共计5种曲线，速度均为300 km/h，以武广谱作为轨道不平顺激励，分析构架关键位置动应力响应，图7给出了侧梁内立板与上盖板焊缝时域与频域图。

结果表明：速度保持不变时，随着曲线半径的减小，侧梁内立板与上盖板焊缝区域动应力呈明显增大的趋势，特别是800 m曲线半径情况下动应力幅值明显大于直线状态。由此说明，曲线半径减小会使车辆稳定性下降，从而导致高速列车转向架构架振动加剧，恶化构架薄弱位置动应力。由图7（b）可知，构架振动能量主要分布在6.75 Hz、11.07 Hz、28.1 Hz、43.2 Hz、63.1 Hz和97.3 Hz附近。6.75 Hz、11.07 Hz和28.1 Hz左右振动能量最大主要是由于高速列车通过曲线时侧滚和离心力作用激发了构架刚体运动模态，其中构架浮沉模态（6.73 Hz）、构架横移模态（11.02 Hz）和构架侧滚模态（27.15 Hz）对构架关键位置动应力贡献较大；43.2 Hz和97.3 Hz附近动应力明显增大是由于激发了构架的扭转模态和菱形变形模态。从图中还可以看出，随着线路曲线半径减小，构架关键位置振动能量逐渐增大，由此说明线路曲线半径变化对构架动应力的影响不可忽略。

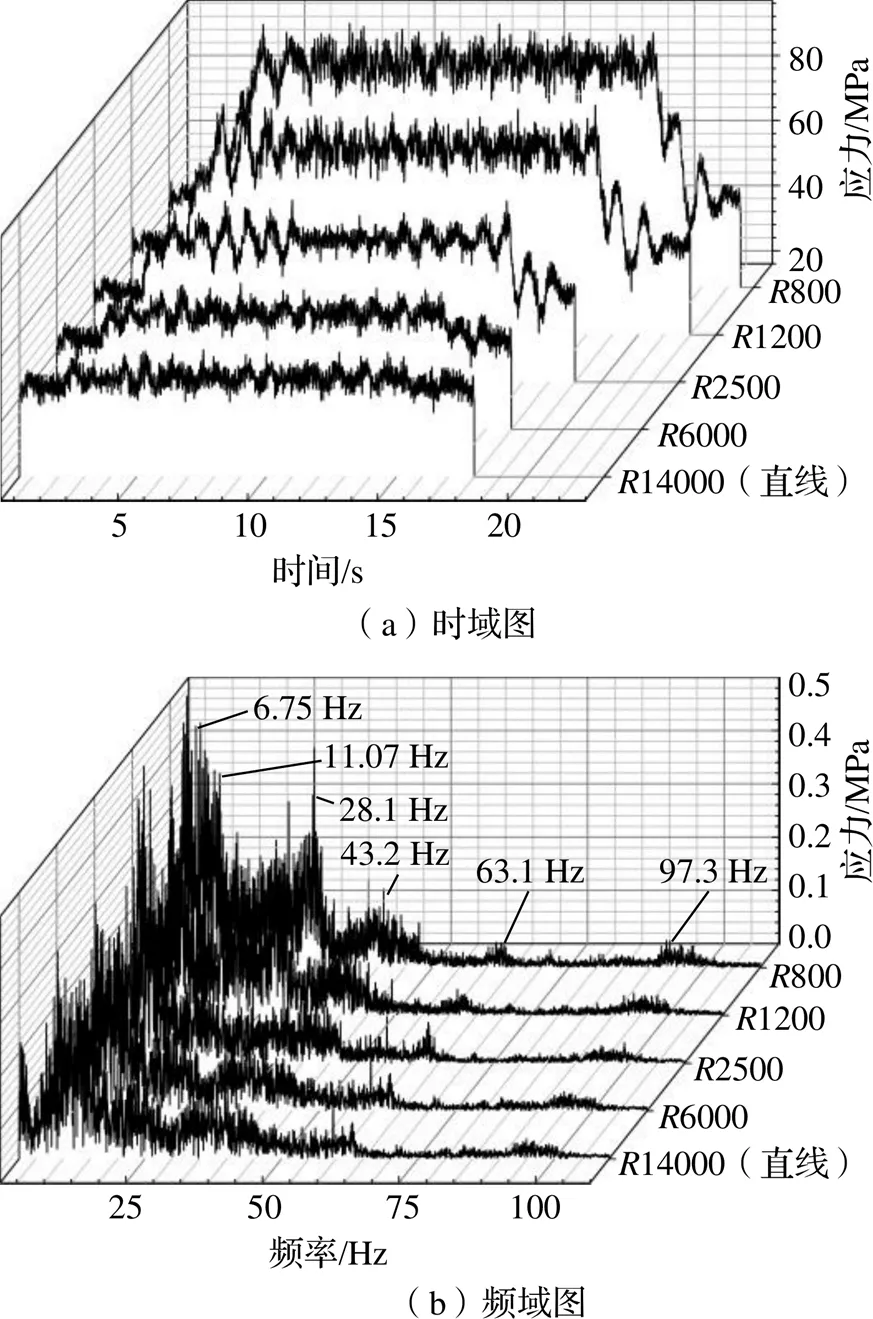
图7 侧梁内立板与上盖板焊缝区域动应力响应时频图

3.2 薄弱位置损伤分析

经验表明，结构的疲劳失效往往起始于结构薄弱位置，本小节主要针对构架几个关键薄弱位置，分析在同一速度不同曲线半径下，动应力对构架关键薄弱位置疲劳寿命的影响。首先基于高速列车刚柔耦合动力学模型计算得到车辆以300 km/h的速度通过1 km不同曲线半径下构架关键薄弱位置的动应力响应，然后基于雨流计数法和国际焊接学会IIW标准规定的焊接接头-曲线（图8），计算构架关键薄弱位置的损伤，如图9所示。

结果表明，小曲线半径（≤3500 m）对构架薄弱位置损伤明显大于大半径曲线和直线，而且当曲线半径小于等于3500 m时，随着曲线半径的减小，动应力对构架薄弱位置的损伤逐渐增大。当曲线半径大于3500 m时，曲线半径对构架损伤的影响基本保持不变。

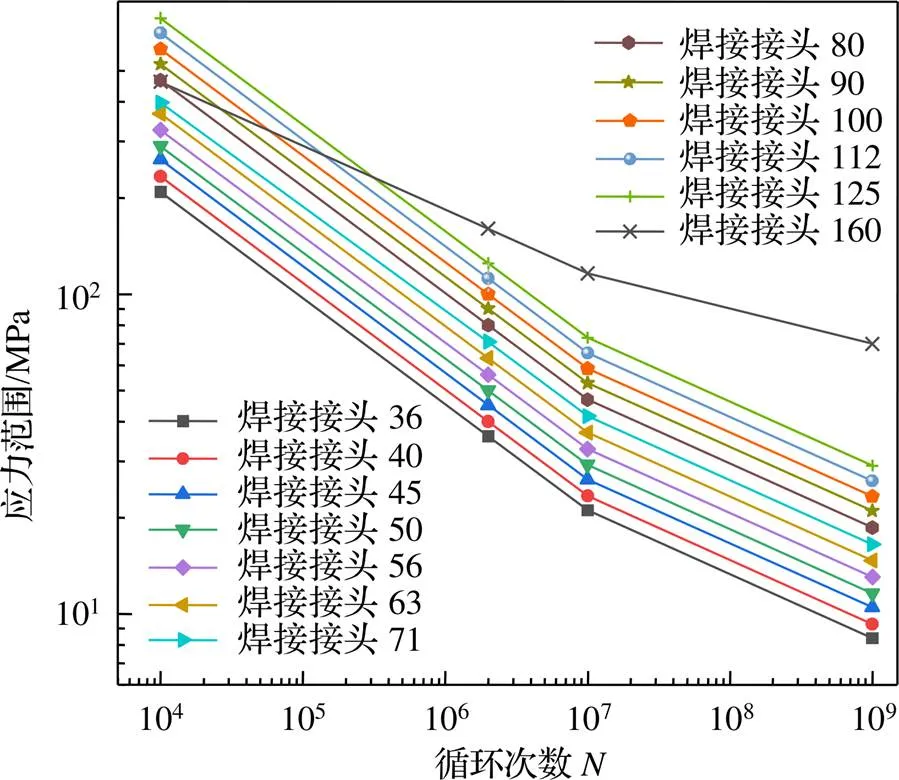
图8 焊接接头S-N曲线

4 高速列车构架振动疲劳寿命预测

高速列车构架作为主要传力部件，其疲劳可靠性是保证车辆高速、稳定和安全运行的关键。本节以京广线线路条件和高速列车刚柔耦合动力学模型为基础，采用威布尔分布和Miner线性累计损伤理论对构架关键薄弱位置的振动疲劳寿命进行预测。京广线全程2298 km，其中曲线半径小于14000 m的线路占总里程的38.49%，如表2所示。对京广线路曲直信息进行统计分析，以威布尔分布进行参数拟合，拟合曲线及参数如图10所示。

表2 京广线路曲直信息

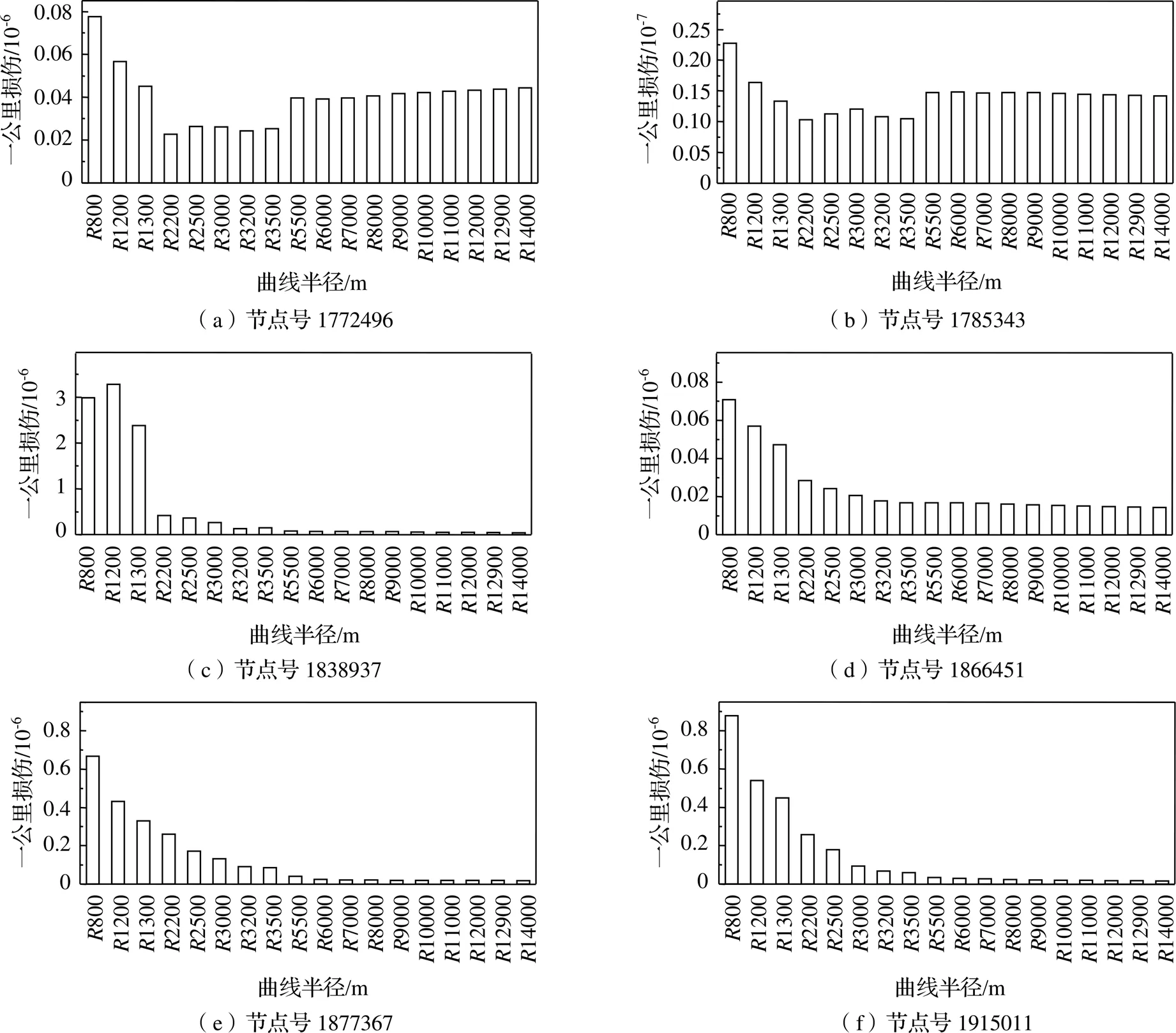
图9 不同曲线半径通过情况下构架关键薄弱位置损伤

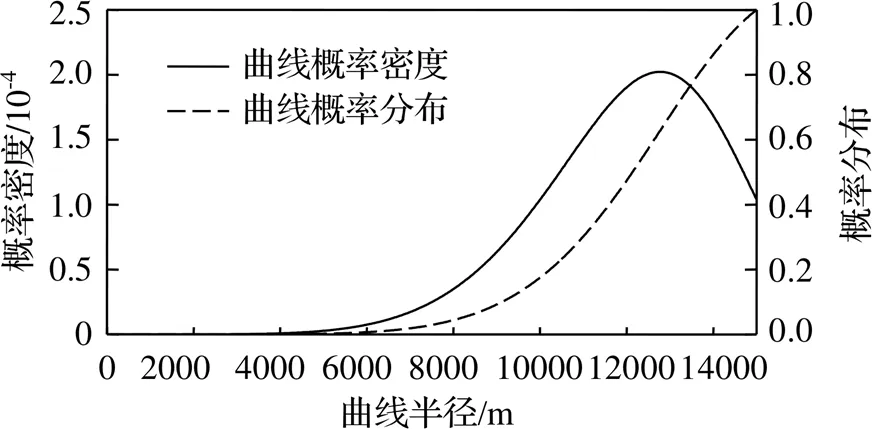
图10 曲线概率密度及概率分布

为反映高速列车通过各曲线半径的实际情况，首先基于图10进行两万个点的随机抽样，模拟高速列车运行两万公里时通过各曲线半径的情况，并根据京广线路实际曲线半径进行区间统计，如图11所示。然后根据Miner线性累积损伤理论和高速列车在不同曲线半径通过情况下构架薄弱位置的损伤（图9），计算得到高速列车运行2万公里时构架关键薄弱位置的损伤，如表3所示。最后将Miner线性累计损伤理论转化为里程公式计算总损伤等于1时的安全运行公里数，如图12所示。

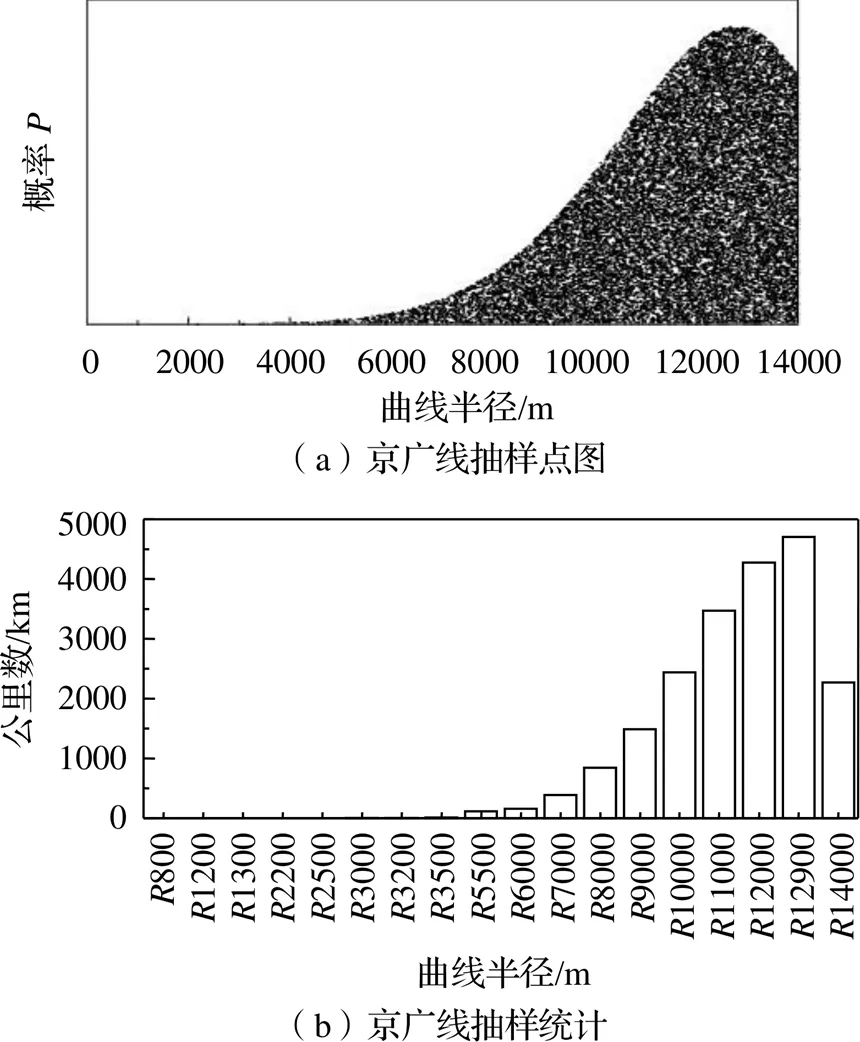
图11 抽样区间及抽样统计

表3 两万公里薄弱位置累计损伤

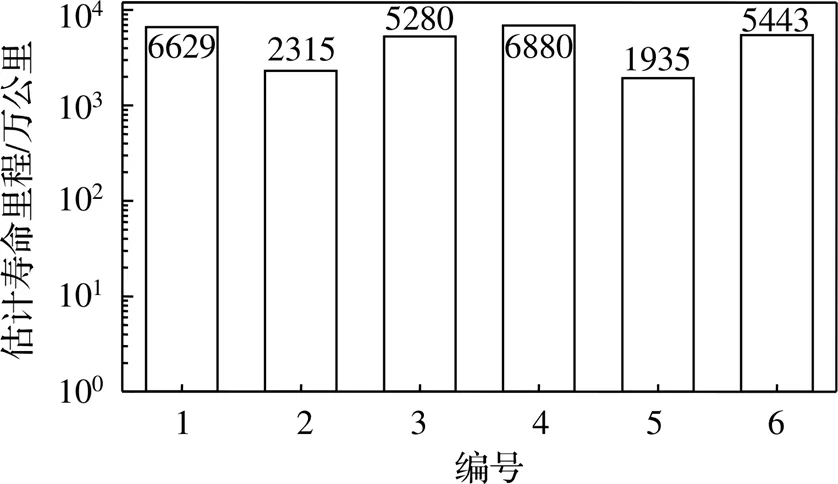
图12 估计寿命里程

结果表明，基于威布尔分布和Miner线性累计损伤原则计算得到最大损伤为1.03×10-3，出现位置为转臂座拐角焊缝区域，预测服役寿命为1935万公里，满足高速列车转向架构架1200万公里的寿命要求。

5 结论

本文基于UIC 615-4对高速列车构架静态薄弱位置进行识别；基于考虑构架柔性的高速列车刚柔耦合动力学模型对构架动态薄弱位置进行识别；研究了不同曲线半径下构架薄弱位置特征动应力，并对构架薄弱位置进行了疲劳寿命预测，可以得到如下结论：

（1）基于高速列车刚柔耦合动力学模型和扫频方法可更加全面地识别构架薄弱位置。构架主要的薄弱位置包括转臂座拐角焊缝区域、横梁与侧梁焊缝区域、侧梁外立板与上盖板焊缝区域、横向减振器座焊缝区域、侧梁内立板与上盖板焊缝区域等部位，弥补了基于现有标准的构架薄弱位置静态识别方法的不足。

（2）在浮沉扫频激励下，构架结构弹性共振对构架动应力影响明显，影响构架动应力的模态主要是构架扭转模态、构架菱形变形模态、构架侧梁同向横弯模态和构架侧梁异向垂弯模态，其中构架菱形变形模态对构架薄弱位置的影响较大。

（3）小半径曲线（≤3500 m）对构架薄弱位置动应力影响明显，当曲线半径大于3500 m时，曲线半径对构架损伤的影响基本保持不变。高速列车在通过曲线工况时，易激发构架浮沉模态、侧滚模态和横移模态等刚体运动模态。

（4）基于威布尔分布和Miner线性累积损伤理论的构架疲劳寿命预测表明，转向架构架最大损伤出现位置为转臂座拐角焊缝区域，预测服役寿命为1935万公里，构架所有薄弱位置预测服役寿命均可满足高速列车转向架构架1200万公里的寿命要求。

[1]DIN EN13749：2011-06，Railway applications-wheelsets and bogies-method of specifying structural requirements of bogie frames[S]. London：European Committee for Standardization，2011.

[2]UIC 615-4：2003，Motive power units-bogie and running gear-bogie frame structure strength tests[S]. Paris：International Union of Railways，2003.

[3]JIS E 4207：2004，Test methods of static load for truck frames and truck bolsters of railway rolling stock[S]. Tokyo：Japanese Standards Association，2004.

[4]吴霜. 高频激励下构架动应力响应与损伤研究[D]. 北京：北京交通大学，2019.

[5]任尊松，孙守光，李强，等. 构架结构振动与动态应力仿真研究[J]. 机械工程学报，2004（8）：187-192.

[6]卢耀辉，向鹏霖，曾京，等. 高速列车转向架构架动应力计算与疲劳全寿命预测[J]. 交通运输工程学报，2017，17（1）：62-70.

[7]王蕾. 转向架构架随机振动疲劳强度分析[D]. 大连：大连交通大学，2019.

[8]朱涛，肖守讷，阳光武，等. 基于频域法的转向架构架疲劳寿命研究[J]. 机械强度，2016，38（1）：160-166.

[9]张丽，任尊松，孙守光. 构架弹性振动对疲劳寿命影响研究[J]. 铁道机车车辆，2015，35（2）：115-119.

[10]乐柄伸，吴兴文，黄运华. 高速列车车体动态薄弱位置及特征应力谱研究[J]. 机械，2020，47（09）：9-16.

Study on Vibration Fatigue of High-Speed Train Bogie Frame Based on Rigid Flexible Coupling Dynamics

LI Chuanying1，LI Peng1，WU Xingwen2，DONG Xiaohua3

( 1.CRRC Qingdao Sifang Co., Ltd., Qingdao 266111, China; 2.School of Mechanical Engineering, Southwest Jiaotong University, Chengdu610031, China; 3.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China )

The rigid flexible coupling dynamic model considering the high frequency flexibility of the bogie frame is constructed, and the dynamic stress of the bogie frame considering the track excitation is solved by combining the modal stress recovery method. According to this model, a method for identifying the dynamic weak position of the bogie frame based on the sweep frequency excitation of typical service mode is proposed, and the stress characteristics of dynamic stress at the weak position of the bogie frame under typical service conditions and damage under each characteristic condition are studied. Finally, on the basis of the distribution characteristics of the Beijing-Guangzhou line, the damage of the weak position of the bogie frame is studied. The results show that the structural dynamic weak position identified based on the sweep frequency excitation of typical service mode includes the static weak position identified by the traditional quasi-static method, and can identify the sensitive frequency band of the weak position. The curve radius has a significant impact on the damage of the key positions of the bogie, and the damage increases significantly with the decrease of the curve radius. Considering the curve and straight-line distribution characteristics of the Beijing-Guangzhou line, the calculated damage at the key positions of bogie frame meets the requirement of the expected total mileage of 12 million km.

rigid-flexible coupled dynamic model of high-speed train；modal stress recovery method；static weak position；dynamic weak position

U270

A

10.3969/j.issn.1006-0316.2023.01.004

1006-0316 (2023) 01-0020-09

2022-04-21

国家重点研发计划（2018YFE0201401）；国家自然科学基金（51805450）；四川省应用基础研究（2020YJ0075）

李传迎（1988－），男，山东聊城人，硕士研究生，主要研究方向为车辆系统动力学和结构疲劳，Email：lichuanying@cqsf.com。*通讯作者：吴兴文（1988－），男，四川成都人，博士，副教授，主要研究方向为振动疲劳，Email：xingwen_wu@163.com。