考虑漏磁和磁饱和的混合悬浮系统控制性能分析

卢相宇，马卫华，罗世辉，刘清辉

考虑漏磁和磁饱和的混合悬浮系统控制性能分析

卢相宇，马卫华*，罗世辉，刘清辉

（西南交通大学 牵引动力国家重点实验室，四川 成都 610031）

相比于纯电磁悬浮系统，混合悬浮系统由于增加了不可控的永磁体，其控制难度增加，且更容易发生吸死状况。本文针对混合悬浮系统的控制性能展开研究。首先，基于混合悬浮电磁铁结构建立其数学模型，利用有限元仿真软件对数学模型进行修正，得到更与实际情况相贴合的数学模型。其次，对系统运动方程进行线性化处理，建立了系统的传递函数，并进行稳定性分析。最后，分别建立PID和模糊PID控制器，并通过SIMULINK模块进行仿真。结果表明，两种控制器均能实现稳定悬浮，但模糊PID控制器超调量更低、防吸死性能更佳，具有更优的控制性能。

混合磁浮；电磁铁；有限元；PID控制；模糊PID控制

中低速磁浮列车因其噪声小、低能耗、运行平稳、爬坡能力强、转弯半径小等优点日渐成为轨道交通行业的研究热点。磁浮列车的悬浮力由悬浮电磁铁提供，悬浮电磁铁的性能直接决定着磁浮列车的悬浮稳定性和悬浮控制的难度[1]。纯电磁结构的悬浮电磁铁利用通电线圈产生电磁力，与F轨相吸，达到列车悬浮的目的。该种电磁铁方案有结构简单、易于控制等优点，但是存在提供的最大悬浮力较小以及电阻损耗较大等问题[2]。随着永磁材料的不断发展和高性能的钕铁硼永磁体的出现，电磁－永磁混合悬浮（以下简称混合悬浮）电磁铁得到了快速的发展。混合悬浮电磁铁的优势在于：在额定悬浮间隙下，列车的悬浮力大部分由永磁体提供，线圈提供小部分悬浮力，起控制调节作用，从而减小稳定悬浮时的电流，能有效解决温升问题[3-5]。因此，混合悬浮系统是未来电磁悬浮的一个发展方向，其控制与工程化目前是磁浮领域的研究重点。

国内外许多学者开展了混合磁浮系统控制性能的研究。CHO等[6]提出了零功率控制策略，并在单自由度动态试验中验证了零功率控制的可行性。KIM等[7]设计了基于扩展龙伯格观测器思想的质量观测器，研究了变质量情况时的零功率控制问题。龙志强等[8]利用线性二次最优控制的方法设计了零功率控制器，在负载变化的情况下仍可实现零电流运行。徐正国等[9]在传统PID控制基础上引入模糊控制和专家控制的思想，建立模糊自适应和专家PID控制器，提高了系统的动态响应速度，减小了跟踪误差。李云钢等[10]基于滑模控制的方法设计悬浮控制器，在实现混合悬浮系统稳定悬浮的同时，使稳定电流保持为零。张文清[11]利用磁通反馈对混合悬浮系统设计了控制器，并通过试验平台进行试验，结果表明基于磁通反馈设计的控制器与传统控制器相比超调量更小，抗干扰能力更强。龙鑫林等[12]基于非线性反馈控制的方法设计了混合悬浮控制器，并提出重构速度信号的方法来减小系统超调量，能有效防止吸死及撞击轨道现象的出现。KUO等[13]结合滑模控制和模糊控制的思想设计了模糊滑模控制器，并进行仿真分析，结果表明模糊滑模控制效果优于单一的模糊控制和滑模控制。

综上所述，国内外学者对混合悬浮电磁铁的研究取得了一系列成果，但在建立悬浮力的数学模型时少有全面考虑漏磁、磁饱和等因素的影响，得到的悬浮力表达式与实际情况有较大差异。针对此问题，本文以混合悬浮系统为研究对象，首先对其结构进行分析，建立其数学模型。再根据有限元仿真结果对数学模型进行修正，使悬浮力表达式中包含漏磁、磁饱和等因素的影响。最后分别建立PID（Proportion Intergal Derivative，比例积分微分）控制器和模糊PID控制器，进行仿真分析对比二者的控制性能差异。

1 混合悬浮系统结构与模型分析

1.1 混合悬浮系统结构

混合悬浮系统简化结构如图1所示，主要包含轨道、永磁体、铁芯、极板、线圈等部件。永磁体与线圈为串联关系，当电磁铁工作在额定工况时，由永磁体提供绝大部分悬浮力，电磁线圈只需提供少部分悬浮力，起控制调节作用，从而达到节能的目的。

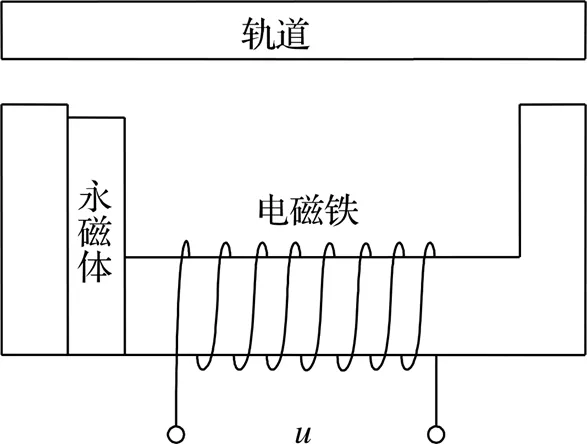
u为电压，V。

为简化模型，做出假设：忽略漏磁及铁芯和轨道的磁阻，可得[14]：

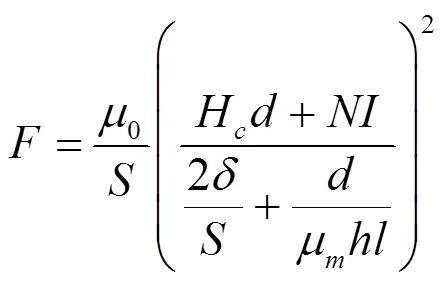
1.2 数学模型修正

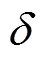
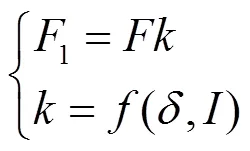
式中：1为修正后的悬浮力，kN；为修正系数。

仿真时设置悬浮间隙值范围为2～16 mm，步长2 mm。通入电流，得到悬浮力随电流变化的仿真值，将式（1）解析计算值与仿真值相除，拟合得到修正系数值。不同悬浮间隙下，悬浮力随电流变化的仿真值和理论值如图2所示，可以看出，随着电流的增加，悬浮力的仿真值和理论值都不断增加，但仿真值在增加到一定值以后增加速率降低，曲线趋于平缓；理论值随着电流的增加，增加速率越来越大。这是因为电流增加大一定值后，轨道、极板和铁芯达到了磁饱和，磁通增加速率降低，但理论公式中并未考虑这些因素，所以理论值与实际值相差较大。

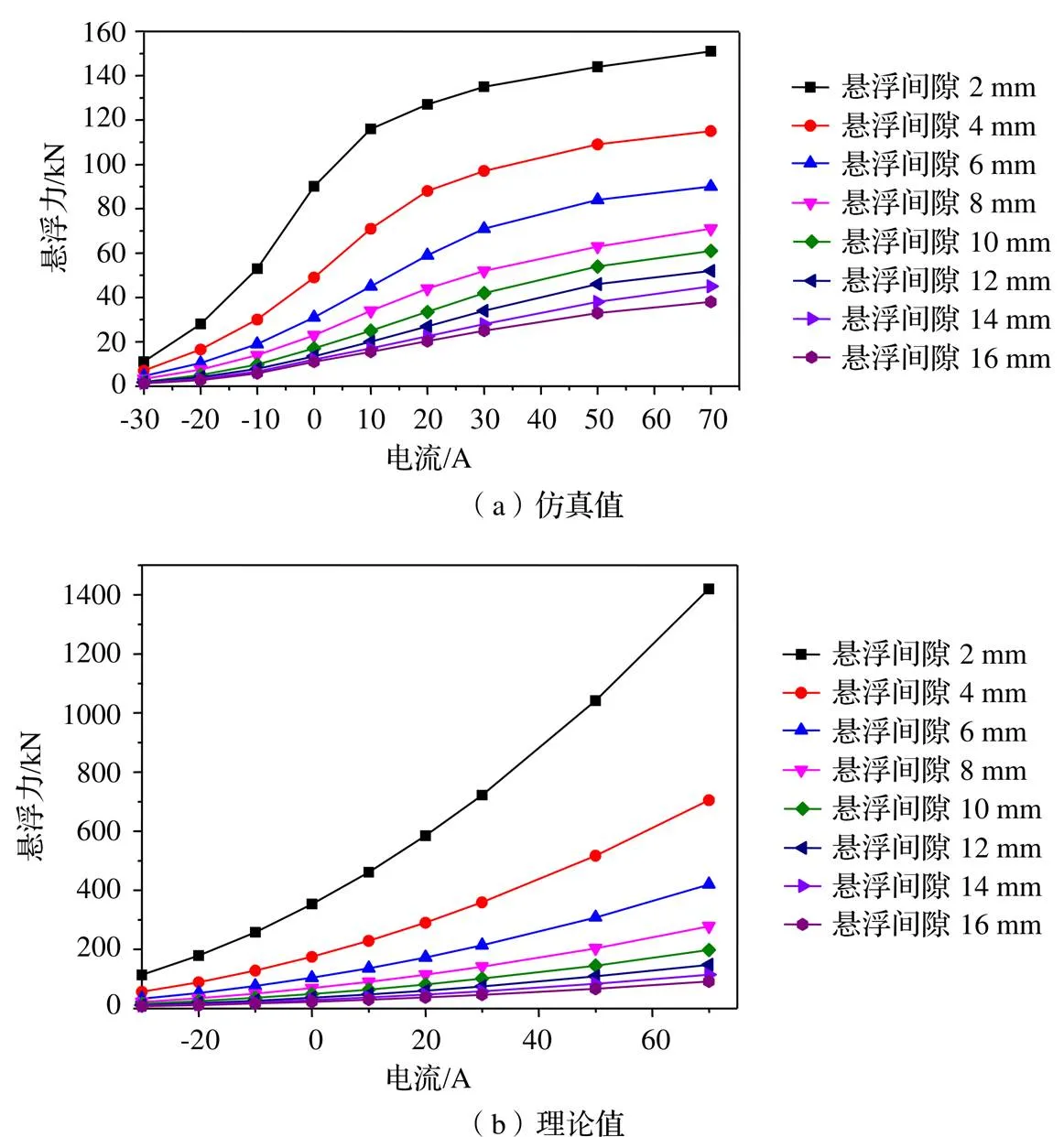
图2 悬浮力随电流变化值

修正系数与悬浮间隙和电流的关系如图3所示，可以看出，随电流的变化呈抛物线，且悬浮间隙不同时，随电流的变化情况也不同。因此用以悬浮间隙和电流为变量的二元多项式来拟合修正系数。

利用1stOpt软件对修正系数进行拟合，得：

为了检验修正系数对漏磁、铁磁材料磁阻及磁饱和效应的修正情况，分两种情况对比拟合公式与有限元仿真结果，如图4所示：①选取悬浮间隙9 mm时，悬浮力随电流的变化情况；②选取电流25 A时，悬浮力随悬浮间隙的变化情况。从图中可以看出，悬浮力的拟合值与仿真值接近，最大误差不超过9%，表明拟合效果良好。

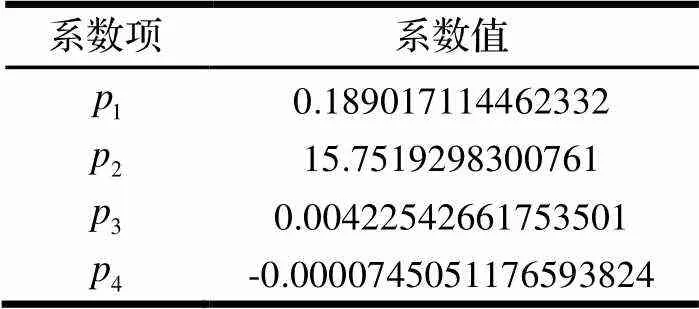
表1 拟合公式各项系数值

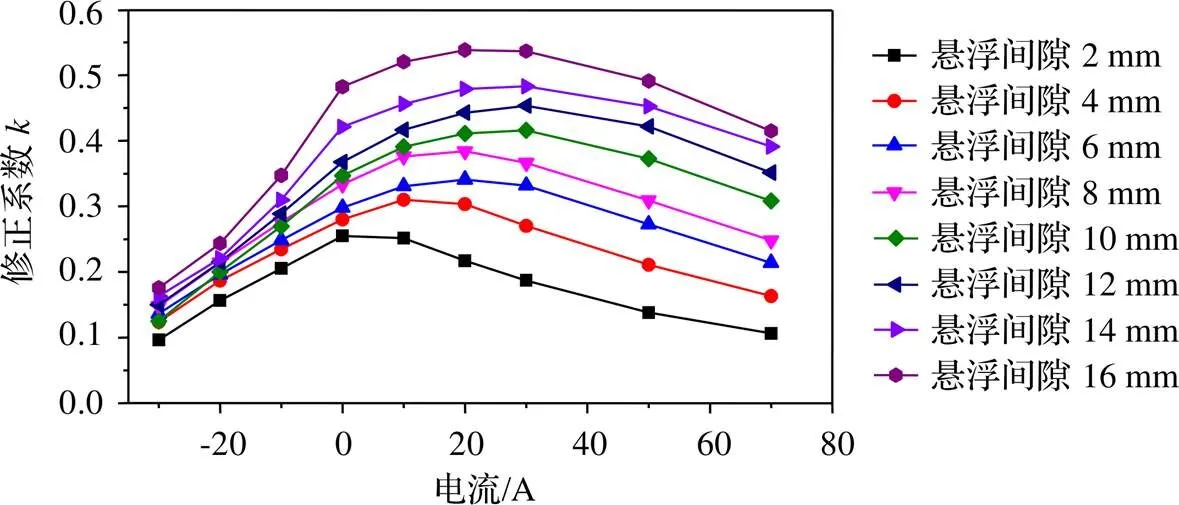
图3 k随悬浮间隙和电流变化值

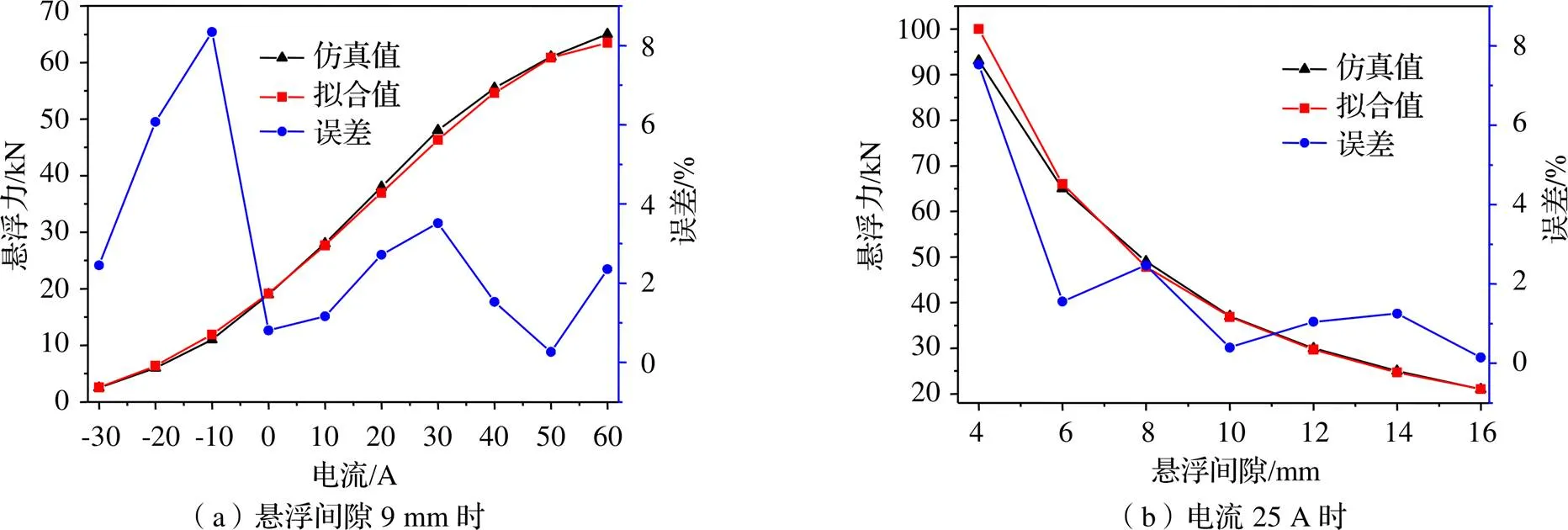
图4 拟合公式和仿真结果对比

1.3 混合悬浮系统模型分析及线性化处理

由前文推导可得：

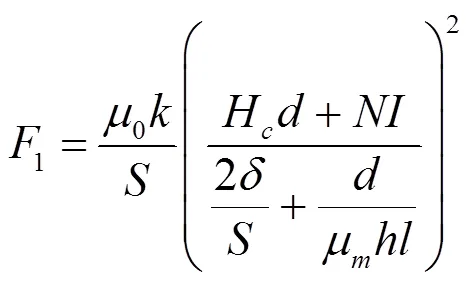
电路中有：

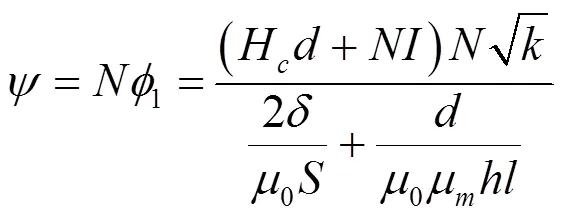
由基尔霍夫定律和楞次定律可得电磁铁中电压与电流的关系为：

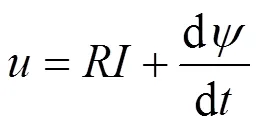
式中：为电阻，Ω；为时间，s。

将悬浮电磁铁看成一个简单力学质点，受到自身重力和悬浮力作用，认为受到的干扰力也在竖直方向。规定向下为正，根据牛顿第二定律，可得到电磁铁的运动方程为：

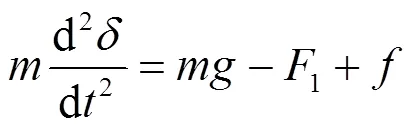
式中：为质量，kg；为干扰力，N；为重力加速度。

本文以新型磁浮列车电磁铁为研究对象，额定8 mm间隙下一块电磁铁提供35 kN悬浮力，需要电流为13 A[15]。

式（5）～（8）为悬浮控制系统的基础模型，且是一组非线性方程，为了利用线性控制理论设计控制器，需对其进行线性化处理。

本文采用泰勒级数展开线性化的方法来得到一个近似的线性化模型。有：

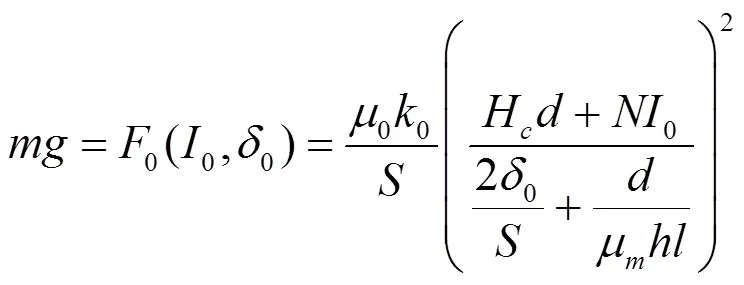
电磁力方程在平衡点处作泰勒级数展开为：

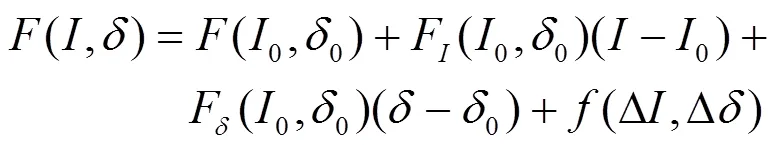
最后一项为高阶项，可以忽略，电磁力方程线性化结果为：

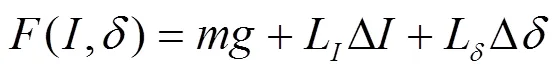
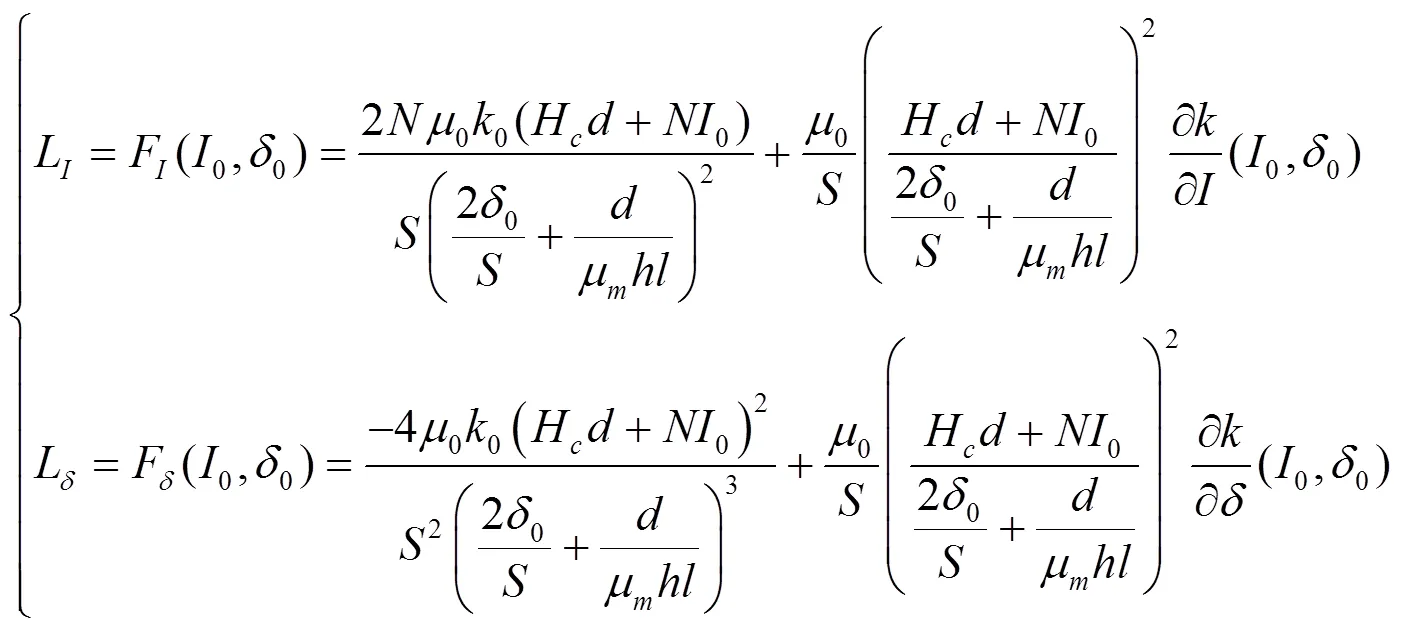
代入相关参数，可得：

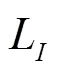
以电流为输入变量，忽略外部干扰力的影响，将式（11）进行拉普拉斯变换，可以得到系统的开环传递函数为：

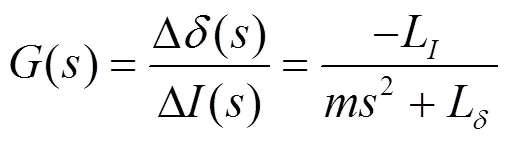
式中：为时间拉普拉斯变换后在虚轴对应的位置。

根据劳斯定理可以得到劳斯判据表，如表2所示。可知，第一列的元素不是全为正，因此可以判定系统存在不稳定的根，系统开环不稳定。要想让系统实现闭环稳定，需要设计控制器进行调节。

表2 开环系统劳斯判据表

2 控制器设计

2.1 PID控制器

因为悬浮系统是一个连续的系统，所以PID控制器的传递函数又可表示为：

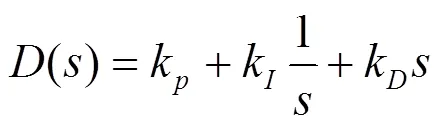
由悬浮系统的开环传递函数和控制器的传递函数，可以得到系统的闭环传递函数为：

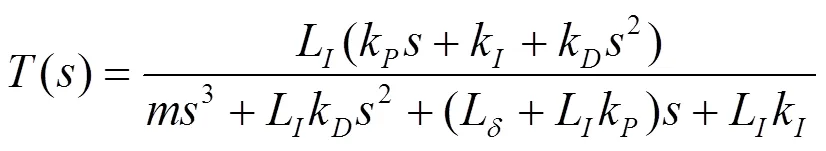
系统的闭环控制结构如图5所示。

为求得具体的控制参数，本文采用极点配置法进行求解。假设得到的闭环传递函数的特征方程可以分解为：

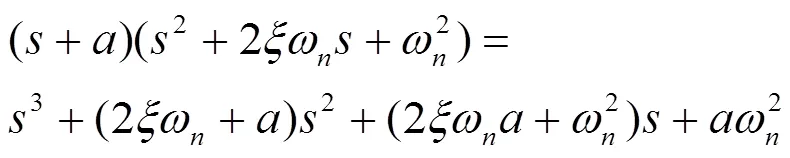
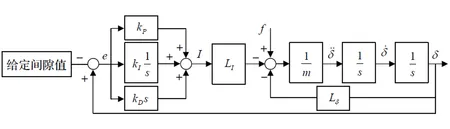
图5 悬浮系统PID控制结构图

有：

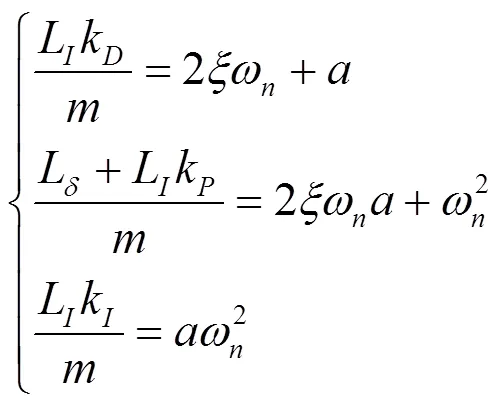
可求得：

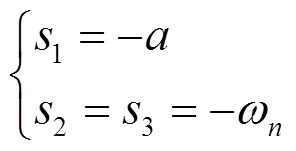
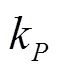
2.2 模糊PID控制器

模糊PID控制系统的基本结构如图6所示，主要针对PID控制器的三个控制参数进行实时调整，增强控制效果。

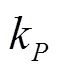
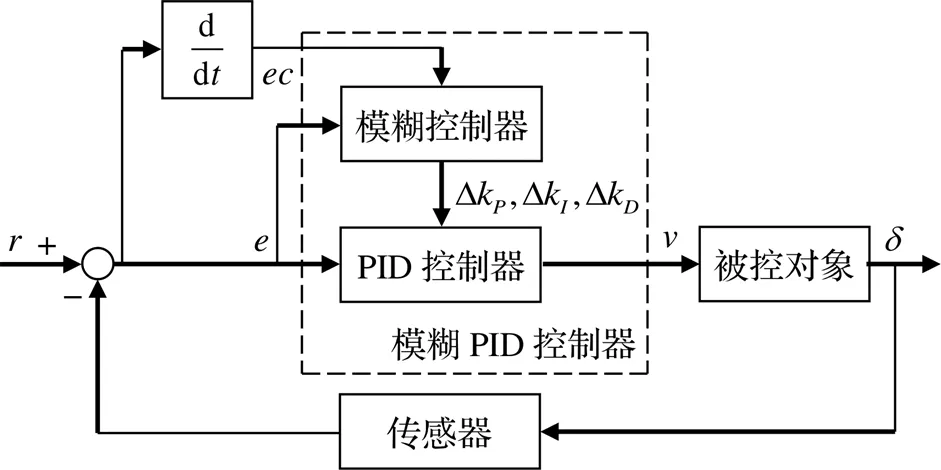
e为偏差；ec为偏差的变化率；r为输入期望值；v为控制器输出。

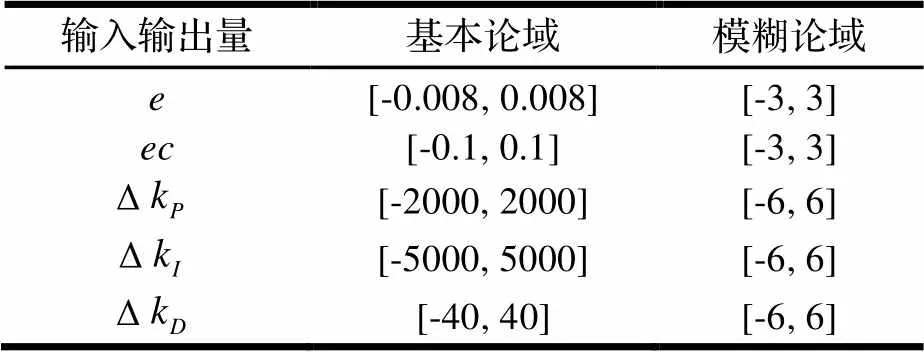
表3 输入输出量的基本论域和模糊论域

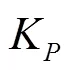
语言变量的隶属度函数如图7所示。采用三角形和高斯型两种类型的隶属函数。

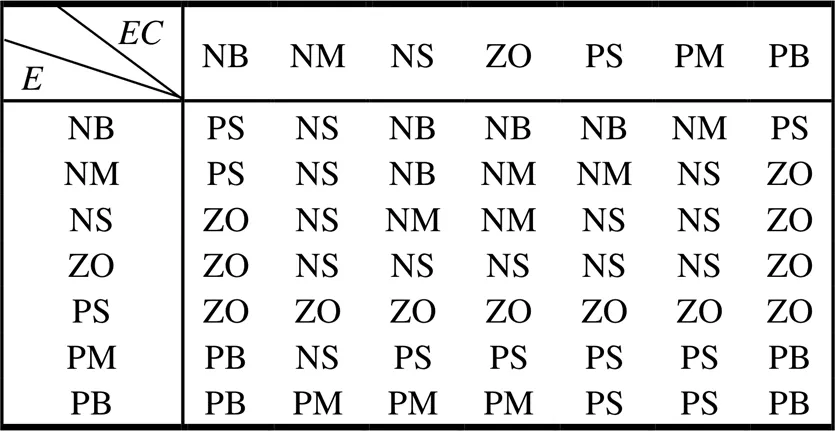
模糊控制规则如表4～6所示。

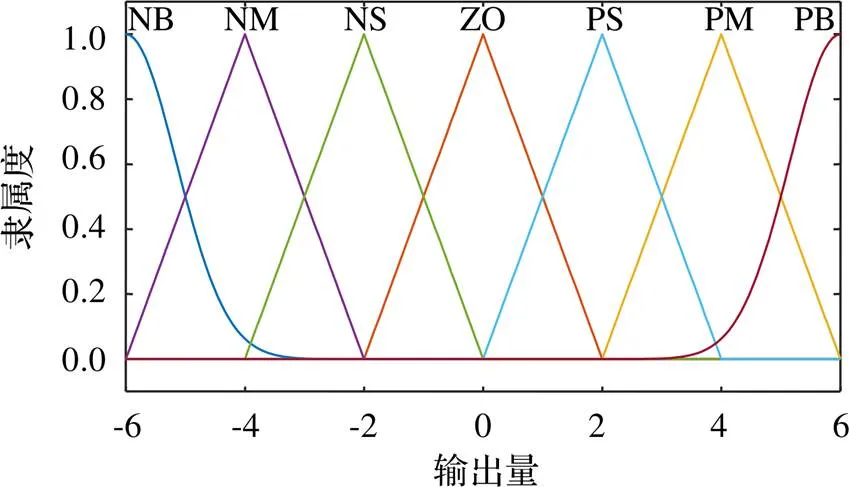
图7 语言变量的隶属度函数

表4 ΔK模糊控制规则表

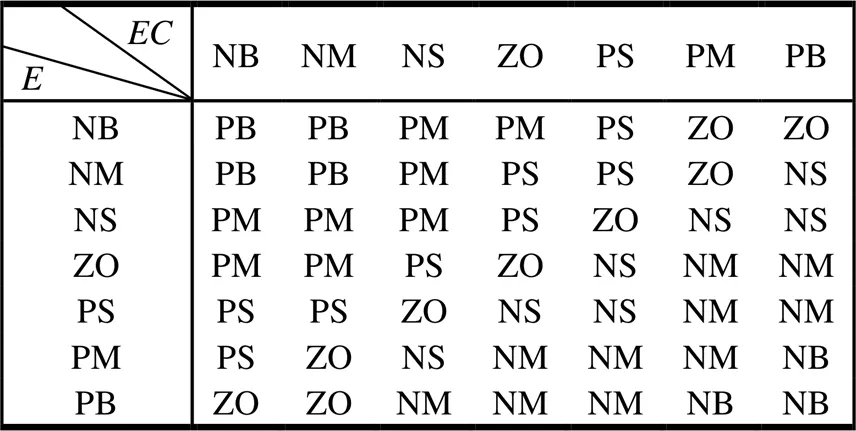
表5 ΔK模糊控制规则表

表6 ΔK模糊控制规则表

3 仿真分析

在SIMULINK中建立控制模型，如图8所示。设置初始的悬浮间隙为12 mm，电流为0 A，平衡点的位置为8 mm，可以得到系统的阶跃响应曲线，此时模糊PID系统和PID系统间隙的波动情况对比如图9所示。可以看出，采用模糊PID控制的系统超调量更小，且达到稳定状态所需的调节时间更短。

为检验系统的防吸死性能，系统在平衡点处运行，在1 s时刻给系统增加一个0.005 mm的间隙阶跃干扰，模拟突发的吸死状况，此时模糊PID控制器和PID控制器间隙的波动情况对比如图10所示。可以看出，模糊PID系统和PID系统均能从吸死工况下回到平衡位置，但模糊PID控制系统回到平衡位置所需时间更短，表明模糊PID控制器具有更强的防吸死性能。

-C-为常数，-K-为增益，均为simulink程序里自带的注释。

4 结论

本文以混合悬浮系统为研究对象，对其控制性能进行探究。通过研究可以得到如下结论：

（1）传统建立的混合悬浮电磁铁数学模型未考虑漏磁及磁饱和等因素，与实际情况相差较大，通过有限元仿真拟合的悬浮力表达式更能反应实际情况；

（2）PID控制器和模糊PID控制器均能使混合悬浮系统稳定，但模糊PID控制器能实时根据系统目前所处状态进行控制参数调整，系统的动态性能更好。在阶跃响应时，系统的超调量更小，且调节时间更短。混合悬浮系统容易出现吸死现象，在模拟突发的吸死工况时，模糊PID控制系统能更快地回到平衡位置，具有更强的防吸死能力。

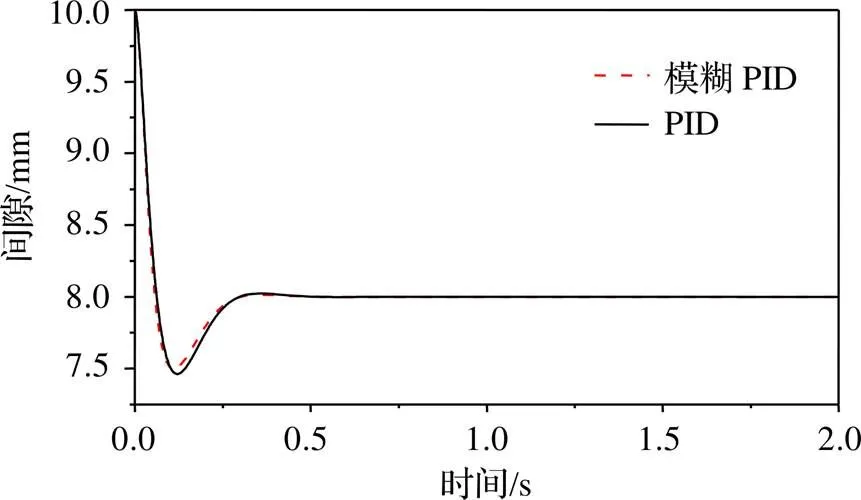
图9 模糊PID和PID阶跃响应曲线对比

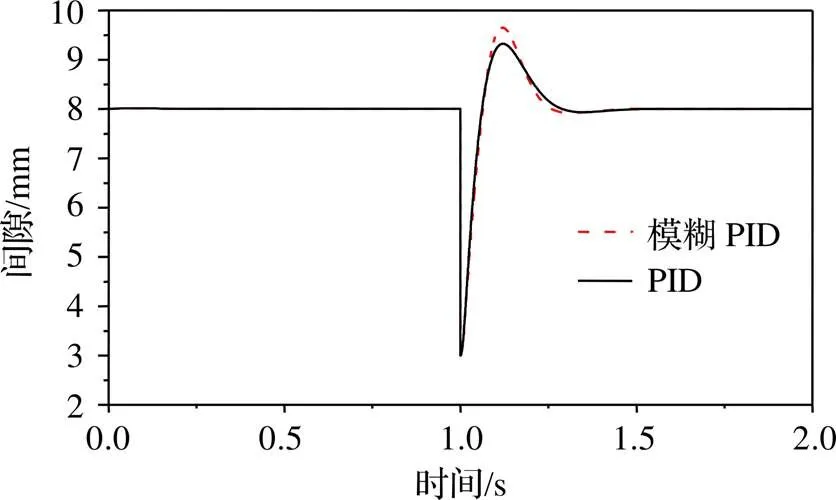
图10 吸死状况下模糊PID和PID控制系统间隙波动对比

[1]刘国清，张昆仑，陈殷. HSST型磁浮列车悬浮电磁铁的优化设计[J]. 微特电机，2013，41（3）：33-35，39.

[2]倪鸿雁. 基于Ansoft磁悬浮列车悬浮电磁铁的动态性能分析[J]. 大众科技，2005（11）：192-193，195.

[3]TZENG Y K，WANG T C. A novel compensating approach for self-sensing maglev system with controlled-PM electromagnets[J]. IEEE Transactions on Magnetics，1995，31（6）：4208-4210.

[4]王永刚，杨君，崔玉萌. 磁浮列车永磁电磁混合悬浮导向系统特性分析[J]. 机车电传动，2021（6）：1-8.

[5]刘少克. 磁悬浮列车用混合悬浮电磁铁温度场建模与仿真[J]. 机车电传动，2011（6）：1-8.

[6]CHO H W，HAN H S，LEE J M，et al. Design considerations of EM-PM hybrid levitation and propulsion device for magnetically levitated vehicle[J]. IEEE Transactions on Magnetics，2009，45（10）：4632-4635.

[7]KIM Y H，KIM K M，LEE J. Zero power control with load observer in controlled-PM levitation[J]. IEEE Transactions on Magnetics，2001，37（4）：2851-2854.

[8]龙志强，周晓斌，杨泉林，等. 永磁式磁悬浮列车系统研究[J]. 机车电传动，1996（3）：8-11.

[9]徐正国，徐绍辉，史黎明，等. 电磁型混合磁极直接自适应模糊悬浮控制方案的研究[J]. 中国电机工程学报，2005，25（18）：157-161.

[10]李云钢，程虎，张鼎. EMS型电磁永磁混合悬浮控制问题[A]. 程代展，胥布工. 第二十四届中国控制会议论文集（上册）[C]. 广州：华南理工大学出版社，2005：928-930.

[11]张文清. 基于磁通反馈的悬浮控制方法研究及实现[D]. 长沙：国防科学技术大学，2014.

[12]龙鑫林，佘龙华，常文森. 电磁永磁混合型EMS磁悬浮非线性控制算法研究[J]. 铁道学报，2011，33（9）：36-39.

[13]KUO C L，LI T H S，GUO N R. Design of a novel fuzzy sliding-Mode control for magnetic ball levitation system[J]. Journal of Intelligent and Robotic Systems，2005，42（3）：295-316.

[14]李云钢，闫宇壮，程虎. 混合EMS型磁浮列车的悬浮磁铁设计与分析[J]. 国防科技大学学报，2006（5）：94-98.

[15]汪科任，罗世辉，宗凌潇，等. 新型磁浮车动力学仿真分析[J]. 振动与冲击，2017，36（20）：23-29.

Control Performance Analysis of Hybrid Suspension System Considering Magnetic Flux Leakage and Magnetic Saturation

LU Xiangyu，MA Weihua，LUO Shihui，LIU Qinghui

( State Key Laboratory of Traction Power, Southwest Jiaotong University,Chengdu 610031,China)

Compared with the pure electromagnetic suspension system, the hybrid suspension system is more difficult to control due to the addition of uncontrollable permanent magnets, and is more prone to suction death conditions. The control performance of hybrid suspension system is studied in this paper. Firstly, the mathematical model is established based on the structure of hybrid suspension electromagnet, and the finite element simulation software is used to modify the mathematical model to get a more realistic mathematical model. Secondly, the motion equation of the system is linearized, the transfer function of the system is established and its stability is analyzed. Finally, the PID and the fuzzy PID controllers are established respectively and simulated by the SIMULINK module. The results show that both controllers can achieve stable suspension, but the fuzzy PID controller has better control performance with lower overshoot and better anti-suction death performance.

hybrid suspension；electromagnet；finite element；PID control；fuzzy PID control

U237

A

10.3969/j.issn.1006-0316.2023.01.001

1006-0316 (2023) 01-0001-08

2022-04-12

国家自然科学基金面上项目（51875483）；牵引动力国家重点实验室自主研究课题（2020TPL_T04）

卢相宇（1996－），男，四川乐山人，硕士研究生，主要研究方向为磁浮列车电磁及控制仿真分析，E-mail：1351612982@qq.com。*通讯作者：马卫华（1979－），男，山东滕州人，博士，研究员，主要研究方向为机车及重载列车动力学、磁浮列车悬浮架设计及列车动力学，E-mail：mwh@swjtu.edu.cn。