基于冗余测量信息的阵列式IMU设计*
魏德轩,曹 乐,张夏丰,张 磊,刘乐远
(上海工程技术大学 电子电气工程学院,上海 201620)
0 引 言
具有成本低、尺寸小和功耗低等优势的集成惯性测量单元(inertial measurement unit,IMU)被广泛应用于导航定位领域[1,2],但其中陀螺仪存在精度低、噪声大的缺点,限制了在高精度场合的应用。为了提高微机电系统(MEMS)陀螺仪的性能,Bayard D S等人在2003年提出了“虚拟陀螺”技术[3],又被称为冗余陀螺、陀螺阵列、批量MEMS陀螺等。其中的关键技术主要包括陀螺冗余系统配置、误差分析与建模、故障诊断和信息融合4个方面[4]。文献[5,6]利用Allan方差对不同IMU阵列的白噪声和零偏不稳定性进行了实验,结果表明噪声性能和IMU数量、空间排列方式相关。即空间排列方式不仅决定了冗余测量所需IMU的数量,还对融合后的白噪声和零偏产生影响。文献[7]推导了冗余比力测量和角速度之间的关系,并利用最大似然估计算法实现了信息融合,同时证明了这种方法也可用于二维阵列布局。
本文按照轴向反向对称、平行正交的安装方式,使用10个ICM20602搭建了硬件平台;针对扩展卡尔曼滤波(EKF)融合算法在使用时由于矩阵维数高,导致求逆运算复杂的问题以及受离群值影响导致滤波收敛速度慢、融合精度下降的问题,使用迭代重加权最小二乘(iteratively reweighted least square,IRLS)对EKF融合算法进行改进,最后利用实验和仿真对算法进行验证。
1 硬件平台
阵列式IMU的性能主要取决于硬件布局和融合算法,对器件进行布局时,需要考虑IMU数量和空间布局对冗余测量可靠性和融合精度的影响。一般而言,IMU数量越多,融合数据精度越高,但是当IMU数量大于10个后,精度提升逐渐减少。再者,同一批次生产的IMU芯片由于材料及生产工艺等原因,具有相同的零偏不稳定性[8],因此,将同一批次的IMU沿敏感轴反向安装,可以将零偏误差影响减小1个数量级。本文为降低零偏误差,采用在印刷电路板(PCB)正反面安装的方式布局。每一面放置5个IMU,其中4个等均匀分布在半径为1.5 cm的圆上,第5个放置在阵列坐标系原点。其中1#,3#和2#,4#IMU的X,Y轴向反向。X,Y的轴向各有4对8个反向对称安装的IMU,Z轴有5对10个反向安装的IMU。圆心位置的IMU提供阵列中心的测量参考值,其中正面原点位置的IMU轴向与融合后的虚拟陀螺仪轴向相同。实物与布局示意如图1所示。

图1 硬件平台实物与布局示意
2 融合算法
一般针对低成本IMU进行噪声建模时,通用误差模型如式(1)所示[9]
(1)
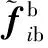
Xk=Xk-1+Wk-1
(2)

传统的阵列IMU布局如图2所示[7,10,11],可以推出此时位置ri处第i个IMU的加速度计输出的比力包括阵列坐标系中心的比力、离心加速度和欧拉加速度,即

图2 比力分解示意
(3)
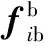

(4)
此时加速度计的比力测量值同时含有角速度和角加速度产生的比力分量。由式(2)可知,角加速度被建模为噪声,此时测量模型与系统模型的噪声相关,无法使用EKF[12]。
本文硬件布局受力分析如图3所示,当分别绕X,Y,Z轴旋转时,可知含有离心加速度分量的加速度计有
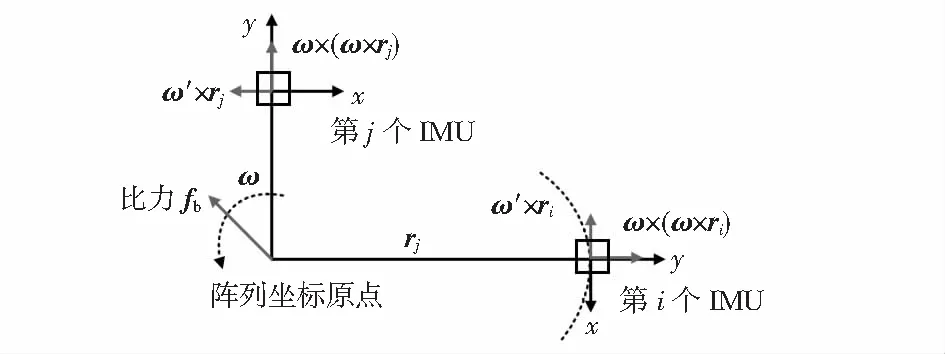
图3 硬件平台输出比力分解示意
(5)
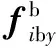

(6)
因此,任意时刻绕过原点的任意轴转动时有
(7)
式(7)中的测量模型可简化为
zi=h(ωi)+ni
(8)
此时,即可使用EKF进行冗余融合。由于IMU距坐标系原点距离相同,任意Y轴加速度计离心加速度项的模都相等,且所有陀螺仪的测量值也都相同。因此可以进行同轴数据融合,降低矩阵维数。目前常用的降维数据融合算法有自适应加权算法、基于支持度和记忆加权融合以及神经网络算法等[13~15],本文采用计算量小、实时性高的IRLS进行降维融合。IRLS伪代码如下:
初始化权重wi(i=1,2,…,N)
(9)
fori=1︰N
(10)
end
式中δ(δ>0)为降权的阈值,β(β>0)为权重相对于残差的衰减率,wk为第k个IMU对应的权重,其中,δ和β需要根据经验值按照需要进行设定。算法整体框图如图4所示。

图4 算法整体框图
经过IRLS降维融合后,角速度10×3维可降为1×3维向量,除圆心外加速度计测量值中的Y轴,根据式(7)可知由8×1降为2×1维向量,另外X,Z轴共8×2维,虽然含有欧拉加速度,本身角加速度可以建模为白噪声误差量级较小,而且在车辆安全驾驶情况下可以忽略,因此可以降为1×2维向量。最终仅使用Y轴加速度计作为观测向量即可,此时维数为2×1维。融合后使用Allan方差法进行噪声参数辨识,确定观测噪声矩阵后进行EKF融合,以上即为本文改进的IRLS-EKF冗余融合算法。
3 实验与仿真
3.1 降维融合算法验证
为验证降维融合算法效果,采集阵列式IMU静止状态下数据,采样频率100 Hz,数据时长2 h。其中,对采集的9个IMU的原始数据不做处理,对第10个IMU加入均值为0方差为0.01 rad/s和0.01 m/s2的高斯噪声模拟异常工作状态。图5分别为陀螺仪和加速度计的X,Y,Z轴的数据降维融合后的Allan标准差曲线对比。

图5 IMU融合数据Allan标准差
图5中位于上端的Allan方差曲线均对应于异常测量数据,此时,离群测量值各项随机误差均明显高于其他IMU。位于下端的Allan方差曲线为采用IRLS降维算法融合后的数据。由图5可知,即使IMU处于异常状态下产生离群测量值,使用IRLS对数据进行加权降维后,融合后的同轴数据的随机误差项零偏不稳定性、角度随机游走和角速度随机游走也明显优于单个惯性器件,角度随机游走大约降低了4~5倍,零偏不稳定性大约降低了3~4倍,证明本文使用的降维融合算法具有较高的可靠性和融合精度。
3.2 冗余融合算法验证
为验证EKF冗余融合算法在运动状态下的效果,使用MATLAB软件的Sensor Fusion and Tracking Toolbox进行仿真验证。为便于对比效果,将陀螺仪的噪声密度的方差设置为4°/s,均值为0的高斯白噪声;加速度计的噪声密度的方差设置为1 mg,均值为0的高斯白噪声。仿真时长共300 s,采样频率为100 Hz。0~75 s,绕Z轴做360 sin(πt/2)°/s的变角速度运动,75~150 s和150~225 s分别绕X,Y轴做360°/s的恒角速度运动,225~300 s同时绕X,Y轴做360°/s的恒角速度运动。通过仿真可以得到IMU的三轴陀螺仪和三轴加速度计的原始数据。根据融合算法(第2节),对Y轴加速度数据进行降维融合后再进行冗余融合。图6为使用EKF进行冗余融合后的数据和陀螺仪测量值对比。

图6 冗余融合后数据对比
图7为运动过程中,使用EKF算法对角速度进行融合后的估计误差与IMU的原始噪声的对比图。根据运动状态可知,Z轴只在前75 s进行融合估计;75~225 s内,X轴和Y轴运动状态类似,因此75~225 s仅使用Y轴估计误差为例进行对比,225~300 s内,使用X轴估计误差为例进行对比。
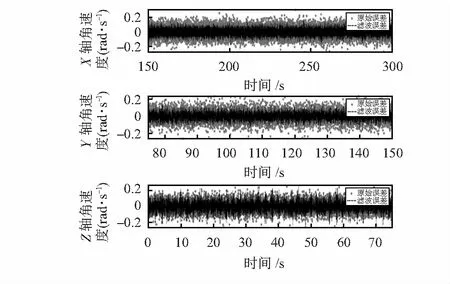
图7 融合估计误差对比
为了评估EKF融合算法效果,经过多次重复仿真试验后,给出了EKF算法的估计误差的方差。
根据表1可知,经过EKF算法进行冗余融合后,X,Y轴提升效果较大,Z轴效果提升较小。原因在于EKF滤波算法受建模精度影响较大,由于Z轴一直处于变角速度运动状态,无法根据运动状态精确调整噪声矩阵,导致融合精度略有下降。整体而言,EKF冗余融合算法依然有效提高了整个系统的测量精度和可靠性。

表1 EKF算法估计误差与原始噪声方差
4 结 论
本文针对MEMS陀螺仪精度低、随机噪声大的问题,在充分考虑冗余配置的可靠性、融合精度的前提下,设计了阵列式IMU硬件平台。并使用IRLS算法对EKF融合算法进行改进,有效降低了离群值的干扰,提高了EKF融合算法的鲁棒性和融合精度。仿真和实验结果表明,本文提出的基于冗余测量信息的设计的阵列式IMU误差小、鲁棒性高,在实际应用中具有较好的应用前景。

