基于双目视觉的堆叠零件识别和定位研究*

刘祚时，范雨婷，陈 飞

(江西理工大学 机电工程学院，江西 赣州 341000)

0 引 言

随着机器人视觉技术的飞速发展，对复杂工况下机器视觉技术的应用提出了更高的要求。目前，机器视觉在工件定位[1,2]、物流分拣[3]、零件装配[4,5]等领域应用广泛。对于复杂场景的三维视觉技术，目前主要有单目、双目、多目、3D扫描及多传感器融合的方式[6]。林义闽等人[7]针对弱纹理特征条件提出一种新的三维重建方法，通过现有设备人工增加纹理特征，重建出三维场景，实现对障碍物的识别与自主导航功能。刘晓阳等人[8]通过激光扫描仪获取场景中散乱工件的点云数据，并利用相关工具获取模型工件精确的点云数据，通过对比两者间点云的旋转平移关系获取位姿信息。周伟亮等人[9]利用深度学习对无序堆叠零件进行模型训练，计算出工件的深度信息。在双目视觉研究中，立体匹配算法是其中的研究热点，也是研究的重点与难点，目前有相位、区域、特征等匹配法[10，11]。

上述方法中存在平台复杂、计算量较大、定位精度低等问题。为了提高堆叠零件的识别定位精度与算法效率，本文提出了一种改进的半全局块匹配(semi-global block matching，SGBM)算法，以圆形线圈骨架为研究对象，采用固定安装双目摄像头方式，搭建实验平台，进行了基于双目视觉的堆叠零件识别与定位研究。

1 系统标定

1.1 双目相机标定

实验选用KS861型号130万像素双目CMOS摄像头，最大分辨率为2 560×960，通过USB 2.0接入计算机。选择12 mm×9 mm的黑白方格的标定板，共计7×8个角点，方格边长为22 mm×22 mm。固定双目相机的安装位置不动，不断改变标定板的位置，拍摄不同的姿态，实验过程中采集多组图片，选取其中的16幅图像，并利用分割程序将其分割为独立的左右视角的图片分别存储在两个文件夹中。在MATLAB中对左右相机图像进行网格处理，将分割好的左右视角的棋盘格的图片导入，自动标记出所有角点，与人工标记的角点相比更加方便、准确，减少了误差，角点标定结果如图1所示。

图1 标定板角点选取情况显示

对标定板图像进行标定对比，排除误差，最终获得重投影误差为0.21个像素，左相机和右相机的参数以及相机的距离关系如表1所示。

表1 相机标定结果

由表1可知，相机标定结果中外参中的旋转矩阵R近似于单位矩阵，平移向量t的第一个参数表示双目相机之间的距离，两相机的实际距离为104 mm，总体标定误差为0.21个像素，小于0.3个像素，在误差允许范围内。

对图像进行校正处理，得到校正后的效果如图2所示。

图2 图像校正结果

通过图像校正，可消除失真和畸变，将左右图像调整为同一平面且行对准，确保了立体匹配的效果。

1.2 手眼标定

将无序堆叠零件放置在具有固定范围的相对固定的料框或置物台平面上，选择常用的“眼在外”(eye-to-hand)的安装方式，相机无需随机械手的运动而运动，计算出相机坐标系与机械手基坐标系间的转换关系。

采用基于双目测量的手眼标定方法，控制机械手末端随机平移3次，旋转1次，线性求解转换矩阵。通过手眼标定中机械手坐标系、像素坐标系相互转换关系，线性求解出旋转矩阵R如式(1)和平移矩阵T如式(2)

(1)

T=[0.654 4,0.457 6,1.170 7]T

(2)

2 堆叠零件的识别与定位

2.1 图像分割

采用形态学处理的彩色标记符分水岭的分割算法[12]，对检测物体用形态学处理后添加彩色标记符，获取准确的零件边缘轮廓图，达到改良过分割的目的。其分割过程如图3所示。

图3 堆叠零件分割过程

为了验证零件分割效果，采用3组不同数量的零件图进行分割实验，不同数量下的图像分割率如表2所示。

表2 不同数量下的图像分割率

结果表明，该算法对3组图像的分割率均在80 %以上，且随着零件数量的增加，分割率提高，分割误差率较小，可以精确地划分出感兴趣区域(region of interest,ROI)。

2.2 改进的SGBM算法

使用双目相机采集线圈骨架零件图，进行立体校正，保证左、右两图像在同一水平面；对于堆叠零件存在遮挡，倾斜的情况，在SGBM算法的基础上进行改进，利用改进的SGBM算法，获取视差图，恢复出零件的三维信息。

SGBM算法继承了全局匹配和动态规划各自的优点，得到了一定程度上的优化，同时避免了原算法的缺点。其算法原理过程分为如下4个步骤：

1)预处理

SGBM算法采用水平Sobel算子进行预处理，其预处理函数如式(3)所示

Sobel(x,y)=2[P(x+1,y)-P(x-1,y)]+P(x+1,y-1)-

P(x-1,y-1)+P(x+1,y+1)-P(x-1,y+1)

(3)

由水平Sobel算子处理的图像上的每个像素被映射到一个新的图像。映射方程如式(4)所示

(4)

式中Pnew为新图像的像素值；P为原图像的像素值；preFilterCap为常数参数(默认为15)。

2)匹配成本计算

SGBM利用最优化能量函数，通过搜索每个像素点的最佳视差，使整张图像的全局函数最小。像素附近的所有路径的一维成本聚合成像素的所有视差下的匹配成本。最后，将归纳的所有一维成本值相加来近似获取二维的最佳值，某像素沿着某一条路径的路径成本计算公式为

Lr(p,d)=C(p,d)+

(5)

式中t1=Lr(p-r,d),t2=Lr(p-r,d-1),t3=Lr(p-r,d+1),t4=Lr(p-r,i),t5=Lr(p-r,k)

3)动态规划

其公式如式(6)所示

(6)

由上式可得总路径成本值S，其表达式如式(7)所示

(7)

4)后处理

通过唯一性检测、亚像素插值、左右一致性检测、连通区域的检测等流程对结果进行相应优化。

经典SGBM算法对整幅图获取视差，弱纹理区和遮挡区存在部分无效点和误匹配点[13]，视差效果差的问题，考虑到背景(弱纹理区)和前景(线圈骨架)重合，背景的误差会干扰前景的匹配，导致前景的视差图不准确，利用孔洞填充的方法，对视差图进行优化的方法，获取更优的视差效果图。算法改进思路为：1)采用设置阈值后的二值化方法进行前景分割；2)采用上下文推理方法对视差图上的“黑洞”进行填充；3)采用RANSAC迭代法剔除误匹配点。

对于遮挡区域的像素点，选取附近背景上的像素点视差。由于前后背景的视差值差异较大，且前景大于背景，故选取所搜集正确视差集合中的较小视差值。选择第二小视差，针对误匹配像素，取视差值的中值。其表达式如式(8)所示

(8)

求取视差结果如图4(a)所示，由于零件本身也存在弱纹理和遮挡现象，会出现误匹配点，以致视差结果有“黑洞”，采用孔洞填充，RANSAC迭代法删除错误匹配点，对视差进行优化，其结果如图4(b)所示。

图4 视差结果对比

改进后的SGBM算法在遮挡区域和弱纹理区仍能达到好的匹配效果，可以较明显的看出零件轮廓图，这样的视差图能很好地提取出目标物体的三维空间坐标点。

3 实验验证

3.1 测量精度实验

对双目测量的精度进行实验验证，其思路是随机标定3个以上的角点，统计多组数据，并依次计算出两点之间的距离，然后与实际测量值作比较，并用误差和均值来验证测量精度。具体步骤为：首先将标定板静置在实验台上，随机标定6个角点，分别记录左右相机像素坐标。

改变标定板位置，重复记录一次，通过计算可获取12组角点坐标值。已知双目相机旋转矩阵R和T，可以计算出这些随机点相对机械手基座的三维坐标，已知各角点的三维坐标值，可以计算出任意两点之间的距离，按角点序号依次计算其距离，再用工具测量出标定板的实际距离，对比2组数据之间的测量差异。计算结果如表3所示。

表3 各角点测量距离与实际距离差值 mm

由表3可知，角点之间距离越远，偏差逐渐增大，但总体而言，2组数据的测量偏差较小，最大为0.62 mm，整体控制在1 mm以内，波动较小。

3.2 定位精度实验

由于手眼标定无法单独验证，联合机械手利用欧氏距离偏差对系统进行定位精度验证，其表达式如式(9)所示

(9)

式中d为角的欧氏距离偏差；xRl，yRl，zRl为坐标集合{Rl}中某点的坐标；xMa,yMa,zMa为坐标集合{Ma}中某角点的坐标。

实验验证过程：首先，不断调整标定板的位置和姿态，进行3次角点定位，选取的棋盘格为7×8，有56个角点，共采集168个角点的三维坐标；然后，将各角点对应的机械手末端坐标与像素坐标转换成的三维坐标点间的空间偏差制成散点折线图，如图5所示。

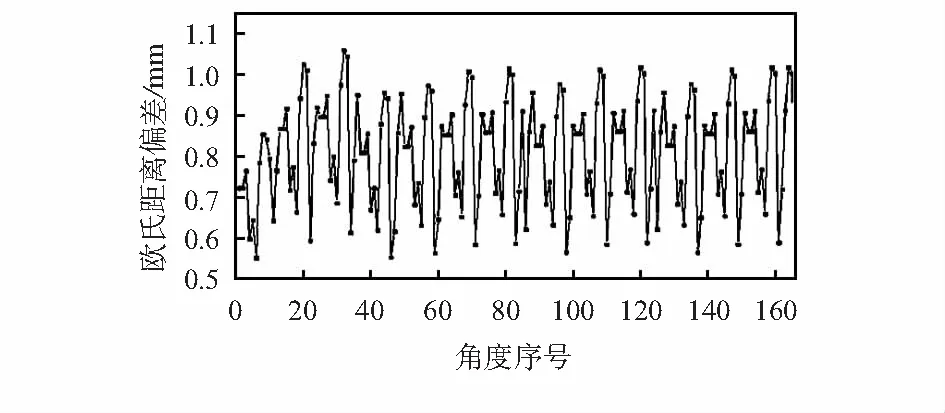
图5 欧氏距离空间偏差图

结果表明，定位精度实验偏差较小，偏差值在0.5～1.1 mm之间波动，偏差均值为0.78 mm。

4 结 论

基于双目视觉的堆叠零件的识别与定位研究，本文通过对SGBM算法进行优化，构建视差图进行立体匹配，对堆叠零件的测量精度和定位精度进行实验验证。实验表明：该双目视觉系统测量误差和定位偏差较小，精度满足一般工业机械手的抓取需求，具有一定的可行性，为后续机械手的抓取奠定了基础，具有一定的实际应用价值。