结构光自标定方法综述*

张美航，张 华，鄢 威

(1.武汉科技大学 冶金装备与控制技术教育部重点实验室，湖北 武汉 430081；2.武汉科技大学 机械传动与制造工程湖北省重点实验室，湖北 武汉 430081；3.武汉科技大学 绿色制造工程研究院，湖北 武汉 430081；4.武汉科技大学 汽车与交通工程学院，湖北 武汉 430081)

0 引 言

三维重构是计算机视觉核心问题之一[1]，相机—投影仪结构光系统是三维重构体系中一个重要分支[2]，结构光系统标定是其众多应用的基础，在某些场景下是其不可或缺的部分[3]。根据标定物不同，标定方法可以粗略地分为基于标定物的传统标定方法和基于场景约束的自标定方法[4]，传统标定方法繁杂且无法在线标定，但精度高[5]；自标定方法操作简单，可以满足一些特殊应用场景[6,7]，但模型复杂且精度、鲁棒性较差[5]。自标定方法是对传统标定方法的补充，结构光系统的自标定是在相机自标定基础上延伸而来，其目的是为了补充传统标定方法存在的缺陷，也是为了简化操作流程。

相机标定和自标定综述文献较多[8～10]，结构光系统标定综述较少。从各类数据库中检索到的文献有刘建伟等人[11]对线结构光系统标定技术的研究，Zhang S[12]介绍了传统编码方法、非传统编码方法以及混合编码方法，给出了部分编码规则原理，并提供了一些实用技巧。王子为[13]提出了一种基于单应矩阵的摄像机自动标定算法，通过对摄像机内外参数进行标定。范剑英等人[14]提出了一种通过一块圆点平面标定板进行标定，再利用自标定算法标定外参。刘顺涛等人[15]研究了基于矩阵变换的摄影测量法、基于几何关系的三角测量法、多项式拟合法3种标定方法，并将3种方法的五大具体标定特性进行了对比分析。任瑜、韩正勇等人[16,17]从其他方面对相机和摄像机的参数标定进行了一些研究。

综上所述，国内外学者对结构光标定方法进行了一些研究和综述，但结构光自标定方法综述在国内外尚未被检索到。本文针对当前结构光自标定方法进行系统综述，对不同自标定方法进行分类归纳，就结构光完全自标定重点论述，且对系统重构效果进行比对；提出结构光自标定方法存在的问题与挑战；指出结构光自标定的可能解决方案及未来发展方向。

1 结构光自标定理论基础

相机—投影仪结构光系统自标定是涵盖相机标定、投影仪标定、相机—投影仪系统标定等科研领域的难点问题，其理论基础主要包括结构光三维重构系统，相机—投影仪标定以及多视角几何中的对极几何等。

1.1 结构光三维重构

相机—投影仪结构光系统一般由数量不等的相机和投影仪组成，投影仪将格雷码、正弦条纹等主动结构信息投射到被测物体表面，再利用单个或多个相机捕获带有结构光图案的被测物表面，再经过图像三维解析实现三维重建[18]。结构光三维重构流程包括相机—投影仪标定、编码[19]、投影编码图案到被测物体、相机捕获带有编码图案的物体表面、解码[20]、三维重构。结构光三维重构示意如图1。

图1 结构光三维重构示意

1.2 相机—投影仪标定

相机—投影仪自标定本质上属于标定问题，标定参数与传统相机和投影仪基本一致。在相机—投影结构光系统中，投影仪往往被看作一个逆相机，因此其需要标定的参数与相机基本相同。相机标定可以分为线性标定和非线性标定，非线性标定除需要正常线性标定外，还需要标定相机畸变参数。相机—投影仪标定示意如图2所示。

图2 相机—投影仪标定示意

1.3 对极几何

对极几何是相机—投影仪自标定的基础。传统标定方法通过已知标定物上特征点之间的尺寸关系构建约束方程从而求解内外参。自标定过程中不涉及标定物，而是利用场景约束构建约束方程，通过求解约束方程[21]来标定相机和投影仪的内外参。对极几何示意如图3所示。

图3 对极几何示意

2 结构光自标定方法归纳

按照相机和投影仪数量不同，对结构光自标定方法归纳如表1所示。

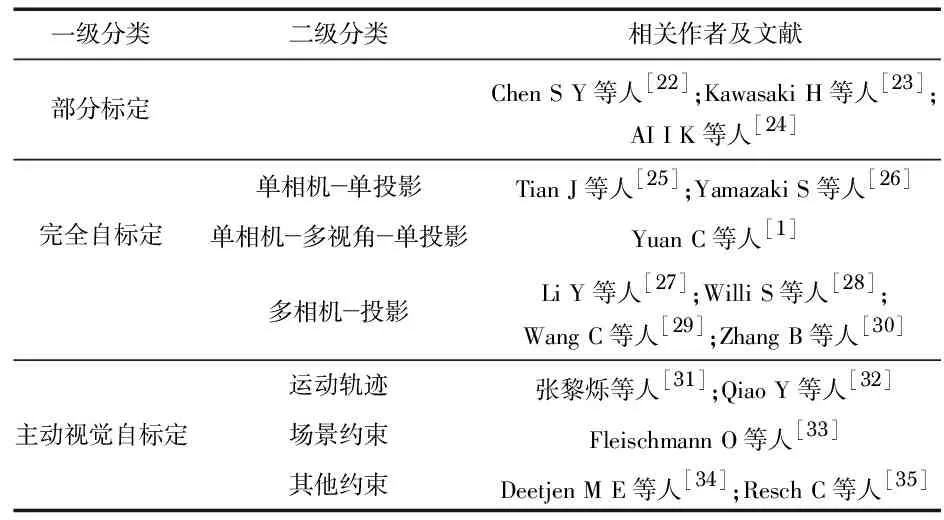
表1 结构光自标定方法归纳

2.1 部分标定

结构光系统部分标定是假设视觉系统中内参或外参部分已知，通过已知参数结合自标定算法求解未知参数，通常已知相机—投影仪内参，标定外参[14,24]。Chen S Y等人在假设已知相机和投影仪内参情况下，提出一种自标定算法获得相机和投影仪的相对位置关系[22]，与之类似的还有文献[23,30]等；AI I K等人[24]提出一种新的标定构架，他们搭建的结构光系统由多个相机和一个投影仪组成，但是投影仪的投影过程由人为设置或者控制；范剑英等人[14]针对双相机—单投影仪的结构光系统进行自标定，内参通过一块圆点平面标定板进行标定，再利用自标定算法标定外参；除此之外，还有Garrido-Jurado S等人[36]的方法均与之类似。

2.2 完全自标定

相机—投影仪结构光系统完全自标定是指标定过程不借助外部标定物，仅通过投影仪投射图像和相机捕获图像对应间关系，构建约束方程，求解相机和投影仪的内外参数[1,2,25,28,36]。完全自标定相比其他自标定方法更具吸引力，针对其技术方案与数学模型进行讨论是有必要的。完全自标定根据标定对象又可以划分为单相机—单投影、单相机—多视角—单投影和多相机—投影的完全自标定。

结构光完全自标定是结构光自标定领域一个重要分支，同时也是一个重点研究内容；自标定结果准确与否，除了比对标定参数外，观察最终重构结果也是一个重要参考指标，重构效果对比如表2所示。

表2 结构光完全自标定重构结果对比

2.3 基于主动视觉自标定

基于主动视觉的结构光自标定方法介于上述两种自标定方法之间，其本身不需要预先对内外参进行标定，但是需要在自标定过程中给定部分已知信息[21]、空间场景[25,30]、运动轨迹[24]等。

3 问题与挑战

相机—投影仪结构光系统自标定方法相比传统标定方法在某些方面具有显著优势，如运动物体在线测量、变焦拍摄等场景，但是，在实际应用的过程中仍然存在一些问题与挑战。

1)精度与鲁棒性方面：与传统标定方法相比，自标定算法在精度和鲁棒性方面存在着明显不足，在不增加外部标定物的情况下利用完全自标定算法精确获得相机内参、外参和畸变参数，是一个巨大挑战。

2)内参假设：当前自标定算法在内参标定时基本都进行了一定假设，例如假设x方向的焦距与y方向的焦距相等，扭曲因子为零等，其原因是当前尚没有合适的数学模型能够求解完全形态的相机内参数。

3)畸变参数求解：当前自标定算法主要是对径向畸变参数进行标定，切向畸变和薄棱镜畸变在目前结构光自标定中考虑很少，因此，结构光系统的非线性自标定有待提高。

4)多相机—投影的同步完全自标定：随着硬件与计算力的快速提升，多相机—投影结构光必然成为未来的趋势，因此，针对多相机—投影自标定算法的研究也将成为一个重点研究方向。然而，到目前为止，针对多相机—投影完全自标定仅有Willi S等人[28]进行研究，而针对多相机—投影同步完全自标定尚无相关研究成果出现。

4 结束语

本文综述了近年来结构光自标定算法的研究状况，发现针对结构光自标定研究较少，完全及同步自标定研究更少，但单相机—单投影的结构光系统标定的研究相对成熟，多相机—投影仪的同步完全自标定尚无有效解决方案。此外，针对相机—投影仪完全自标定技术方案从底层数学模型进行阐述，面对当前结构光自标定算法中存在的问题，给出一些可能的解决方案。

未来，将设计目标函数时以约束项的形式考虑之前通过假设舍去的内参和畸变参数，引入深度学习对约束项参数进行调整和优化，通过迭代进行求解；针对多相机—投影结构光系统同步完全自标定，考虑分解为多相机系统自标定和单相机—单投影同步完全自标定两个过程，分别设计求解函数，最后将两个目标函数整合为一个总的目标函数，通过迭代求解达到全局最优，从而实现多相机—投影结构光系统的同步完全自标定。