完全网络图的出边-平衡指数集
熊晓蓓, 白雨杰, 毋述斐
(1.河南理工大学 数学与信息科学学院, 河南 焦作 454003; 2.河北张家口蔚县西合营中学, 河北 张家口 075700)
图的标号问题是离散数学与理论计算机科学领域中的一个重要研究课题,其主要通过对图的顶点或边进行标号,进而研究图的各种内在特性.标号理论的研究成果被广泛应用于编码理论、X-射线晶体学、雷达、天文学、电路设计、通信网络寻址、数据库管理和网络密码等领域[1-3].
边-友好标号及边-平衡指数集的概念首先由Kong和Lee在文献[4]所提出.从算法角度, Chen等[5]人证明了一个图是边-平衡的不是NP-难问题. 从集合论角度,学者们通常关注一些特定的图类, 寻求其边-平衡指数集.例如, 刘金萌等[6]得到了两类幂圈嵌套图的边-平衡指数集. 郑玉歌等[7-9]得到了幂圈嵌套网络图的边-平衡指数集. Sinha 和 Kaur[10]得到了星图,二正则图,轮图和图mPn的边-平衡指数集, 在文献[11]中进一步地研究了双星图, 扇形和广义的扇形图及网格图P2×Pn的边-平衡指数集.Shiu[12-13]确定了完全二部图的边-平衡指数的极值并进一步确定了完全二部图的边-平衡指数集. Vinutha等[14]确定了Cn×P3,Kn,n的边-平衡指数集. Xing等[15]给出了扇图的边-平衡指数集.本文将边标号的概念推广到有向图, 通过对标号矩阵的研究, 确定了友好标号下完全网络图的出边-平衡指数集.
1 预备知识
令G是一个简单连通图,它的点集和边集分别记为V(G)和E(G),如果一个图既没有环也没有平行边,则称它为简单图.
定义1 称映射f:E(G)→2为图G的一个边标号.用Ef(0),Ef(1)分别表示在映射f作用下标号为0或1的边集合,用ef(0),ef(1)分别表示这两个集合的基数.
定义2 设f是图G的一个边标号.如果|ef(1)-ef(0)|≤1,则称标号f是边-友好的.
令D是一个简单有向图,其点集和弧集分别为V(D)和E(D).D的边标号及边-友好标号均可按照上述定义得到.对于任意顶点u∈V(D),它的出边集是指以该顶点为起点的边集合{uv|v∈V(D),uv∈E(D)}.类似的,入边集指以该顶点为终点的边集合{vu|v∈V(D),vu∈E(D)}.下面给出有向图出边-平衡指数集的概念,它可看作无向图边-平衡指数集概念在有向图中的推广.
定义3 设f是有向图D的一个边标号.由f诱导出的点标号f+:V(D)→2定义为:∀u∈V(D),
对i∈2,标号为i的点称为i-点.用Vf(0),Vf(1)分别表示0-点或1-点的集合,用vf(0),vf(1)分别表示这两个集合的基数.
定义4 设D为一有向图,称集合{vf(1)-vf(0)∶f是边-友好的}为D的出边-平衡指数集.
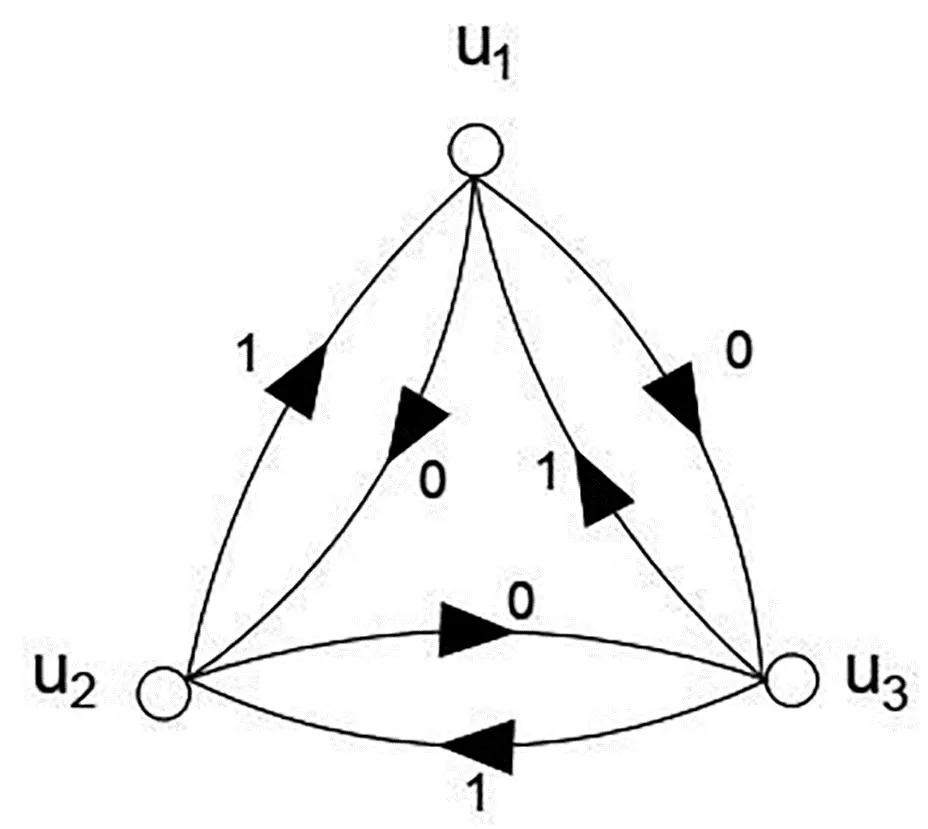
图1 标号图
定义5 图G在边标号f下的标号矩阵Lf(G)是一个行和列均对应G中的点得到的指示邻接矩阵,用xij表示第i行第j列的元素,则
由定义5知给定一个图,它的一个边标号会对应一个标号矩阵.反之,任意给定一个该图的标号矩阵我们也能将其还原为图的一个边标号.即图的边标号与标号矩阵间存在着一个一一对应(双射).这为我们利用矩阵来研究边标号问题提供了保证.

其中: 第i行对应点ui,第j列对应点uj,且对任意i,j,xij=0或1.为了便于计算,移除矩阵对角线上的*得到一个新矩阵(仍称为标号矩阵),将新得到的矩阵记为A,如下所示:
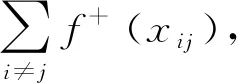
(1)A中的每个元素是1或者0;
(2)eA(1)=eA(0).
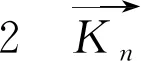
设Jm,n是m×n元素全是1的矩阵,Om,n是m×n元素全是0的矩阵,为构造所需的友好矩阵,首先做如下子阵设计, 对于k≥1,令

本文所需矩阵变换,将按照下述操作进行.
步骤B:令B0是一个2s×n的友好矩阵,当1≤i≤s时,矩阵Bi通过矩阵Bi-1交换(Bi-1)i,1和(Bi-1)s+i,1得到.
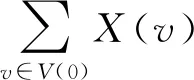
下面对n取值分4k,4k+1,4k+2,4k+3四种情况进行讨论.
情况1:n=4k,k≥1.
由引理1知,0≤s(A)≤4k且s(A)为偶数.对于任意j∈[0,2k],下证存在友好矩阵A使得s(A)=2j.
令A0=(A4k,4k-4|Jk,1⊗A4,3),显然s(A0)=0.对A0的k个子矩阵A4,3逐个进行步骤B,可以得到2k个矩阵,其s-值取遍2到4k之间的所有偶数.
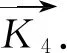
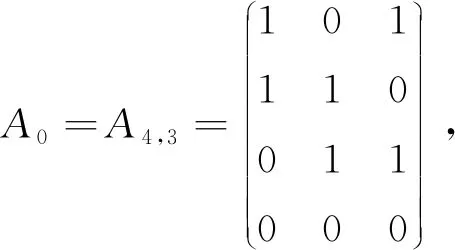
这些矩阵对应的s-值为0,2,4.
情况2:n=4k+1,k≥1.
由引理1知,0≤s(A)≤4k且s(A)为偶数.对于任意j∈[0,2k],下证存在友好矩阵A使得s(A)=2j.
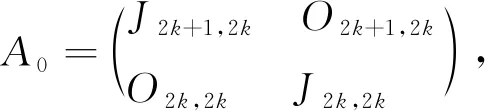
当1≤i≤2k时,在矩阵Ai-1基础上通过交换(Ai-1)i,1和(Ai-1)2k+1+i,1得到矩阵Ai,易得s(Ai)=2i.


这些矩阵对应的s-值为0,2,4.
情况3:n=4k+2,k≥1.
由引理1知,0≤s(A)≤4k+1且s(A)为奇数.对于任意j∈[0,2k],下证存在友好矩阵A使得s(A)=2j+1.
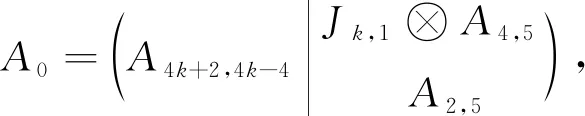


这些矩阵对应的s-值为1,3,5.
情况4:假设n=4k+3.
由引理1, 0≤s(A)≤4k+3且s(A)为奇数.对于任意j∈[0,2k+1], 下证存在友好矩阵A使得s(A)=2j+1.
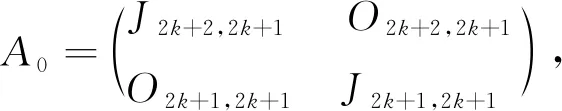
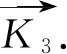

由引理1和上面四种情况可以得到
3 结束语
通过构造标号图对应的标号矩阵,利用矩阵变换、子矩阵设计的方法研究了有向图的边-友好标号,确定了完全网络图的出边-平衡指数集.由于标号矩阵与标号图之间存在一一对应,利用指数集证明中所构造的标号矩阵可以很快做出相应的边标号图.标号矩阵的方法对于其他图类的边-友好标号及边-平衡指数集的研究或许也有参考价值.

