禁用的图α-谱半径极值问题
周金秀, 王文环
(上海大学 数学系, 上海 200444)
本文考虑的图都是无向且无重边的简单连通图.设H=(V(H),E(H))是具有n个顶点的图,其中V(H)和E(H)分别是图H的顶点集和边集.图H中一个顶点的度定义为图H中与这个顶点关联的边条数.如果H的所有顶点都具有相同的度k,那么称H是k-正则的,其中k≥1.一个k-正则图H称为(k,a,c)强正则的,当且仅当H中每对相邻的顶点都有a≥0个公共邻居,每对不相邻的顶点都有c≥1个公共邻居.令A(H)和D(H)分别是图H的邻接矩阵和度对角矩阵.对于任意0≤α≤1, Nikiforov[1]提出研究A(H)和D(H)的凸线性组合Aα(H)矩阵,且将其定义为:
Aα(H)=αD(H)+(1-α)A(H).
图H的α-谱半径,记为ρα(H),其定义为Aα(H)所有特征值中的最大值.
如果0≤α<1且H连通,那么Aα(H)是不可约的.根据Perron-Frobenius定理,它具有唯一的单位正特征向量x=(x1,x2,…,xn)T与ρα(H)相对应.我们称这个向量x为H的α-Perron向量[1].令di是图H中第i个顶点的度,其中1≤i≤n.有
(1)
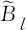
Brualdi和Hoffman[2]提出了谱Turán型极值问题:在不包含给定子图的图类中,研究谱半径的最值问题,并刻画取得极值谱半径的极值图.谱Turán型极值问题是图谱理论中一个重要且有趣的问题,吸引了很多学者的关注,人们获得了丰富的研究成果,对其详细了解,可参见综述文献[3-5].下面,本文重点阐述当禁用子图为Bl和Ks,t的谱Turán型极值问题的研究进展.
2007年,Nikiforov[6]在禁用{Bk+1,K2,l+1}的简单图中,得到了谱半径的上界.2007年,Shi和Song[7]在禁用{Bk+1,K2,l+1}的简单图中,刻画了具有最大谱半径的极值图.2009年,Babai和Guiduli[8]在禁用Ks,t的简单图中,证明了此类图谱半径的上界.2010年,Nikiforov[9]使用不同方法改进了Babai和Guiduli[8]的结果.2016年,De Freitas等[10]在禁用K2,s+1的简单图中,得到了具有最大无符号拉普拉斯谱半径的上界,并刻画了达到上界的极值图.2017年,Kong和Wang[11]不仅在禁用Ks,t的简单图中,给出了无符号拉普拉斯谱半径的上界,而且在禁用{Bk+1,K2,l+1}的简单图中,得到了无符号拉普拉斯谱半径的上界,并刻画了达到上界的极值图.
1 主要结果
为了得到本文的主要结果,下面引入引理1和引理2.
引理1设H是具有n个顶点且最大度为Δ的连通图.则

ρα(H)=xTAα(H)x
≤αΔ+(1-α)(xTA(Kn)x-2∑vivj∉E(H)xixj)
≤αΔ+(1-α)(n-1)-2(1-α)∑vivj∉E(H)xixj.
上式经过整理,得到引理1.
引理2设H是具有n个顶点且最大度为Δ的连通图.则
证明令x=(x1,x2,…,xn)T是H的α-Perron向量.则
ρα(H)=xTAα(H)x
下面给出本文的主要结果定理1.
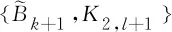
等号成立当且仅当H是顶点数为n的完全图,且Δ=n-1,2k=n-2,l=0.

≤2k∑vpvq∈E(H)xpxq+l∑vpvq∉E(H)xpxq.
(2)
根据Aα(H)x=ρα(H)x,有
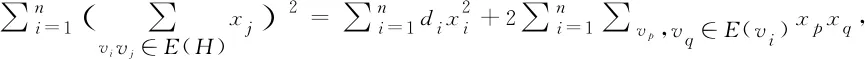

由于[2αΔ+2(1-α)k]α+[-α2Δ-2α(1-α)k+(1-α)2]=α2Δ+(1-α)2,上式可化为
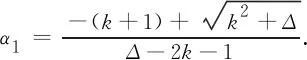
(3)
令[2αΔ+2(1-α)k]+f(α)-(1-α)l=(2k+1-Δ)α2+(2Δ+l-4k-2)α+2k+1-l=P.令Q=4(1-α)l[αΔ+(1-α)(n-1)].经过整理,(3)式可化为
(4)
由(4)式,可以推出
(5)
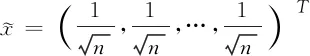


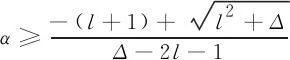
2 结束语


