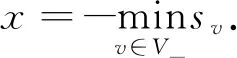无三角形图的符号边控制数下界

潘晨佳, 曾庆厚

(福州大学 离散数学与理论计算机科学研究中心, 福建 福州 350003)

近几年来,图的控制理论研究的内容越来越广泛,各类图的控制概念相继产生且研究成果不断丰富.关于图的符号控制理论,其实早在1995年,Dunbar,Hedetniemi,Henning等人[1]就提出了图的符号控制概念.近些年来,学者们对符号控制理论深入研究,得到了大量的研究成果.图的符号控制理论,有着广泛的应用背景,例如在计算机网络、交通运输、电网检测[2,3]等方面.然而几乎所有的概念都是与图的点控制相关, 很少涉及图的边控制问题.因此,徐保根[4]提出了图的边控制概念,并且研究了几种类型的图边控制问题,提出了相关问题[5,6].

图G=(V,E)是一个简单的有限无向图,其中V表示图G的顶点集,E表示图G的边集.考虑图G中的任意一个点v∈V,任意一条边e=uw∈E,我们用N(v),N(e)分别表示点v的所有邻点构成的集合以及与边e=uw有公共端点的所有邻边构成的集合,用N[e]=N(e)∪{e}表示e边的闭邻域.考虑子集S⊆V,G[S]表示子集S在图G中的导出子图.

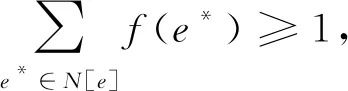
E+={e∈E|f(e)=+1},E-={e∈E|f(e)=-1}.

定义顶点数为n的图的符号边控制数

问题1[4]: 对于任意顶点数为n的图,其符号边控制数g(n)是多少?

目前对于这个问题的研究,学者们得到了符号边控制数的下界并且不断进行优化:2009年,Akbari,Bolouki,Hatami等人[7]提出:对于任意正整数n,有g(n)≥-n2/16;2022年,Cherkashin,Prozorov[8]对这一下界进行改进,证明了对于任意顶点数为n的图,都有g(n)≥-n2/25.在文献[9-11]中,研究了更多关于边控制的问题.

在本文中,我们将讨论无三角形图的符号边控制数g(n)的下界,并得到了以下的结果:

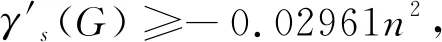
g(n)≥-0.02961n2.

1 前期准备

本章节将给出本文定理1的证明中会用到的定理、引理及其证明.

引理3对于自变量为实数k,b的优化问题

(*)

不妨假设k1∈[0,1],b1∈[0,1],满足当k=k1,b=b1时,上述式子(*)达到最小值.

max(f(k1,b1),h(k1,b1))≥h(k1,b1)

max(f(k1,b1),h(k1,b1))≥f(k1,b1)

根据以上两种情况,我们容易得到

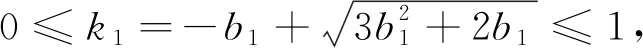
对T(b)进行求导,得到

当T′(b)时,则有18b3+18b2+3b-1=0.我们可以得到, 当

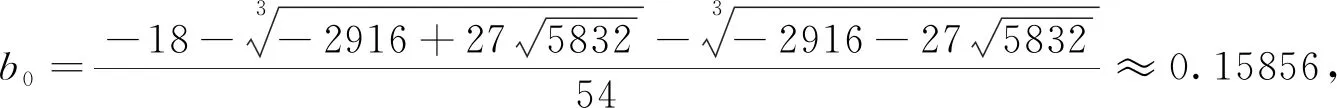
有T′(b0)=0.并且当b>b0,有T′(b)>0;当b

2 定理1的证明

证明 设G=(V,E)是一个无三角形的图,顶点数为n,f是图G的一个符号边控制函数.根据符号边控制函数f的定义,对于图G中的任意一条e=uv∈E(G)边都满足su+sv-f(e)≥0,所以我们可以得到sv+su≥0.显然我们可以将顶点集分为两部分V=V+∪V-.

如果V-是个空集,那么显然有

则定理1定成立.所以我们考虑V-非空的情况.

sy=|N+(y)|-|N-(y)|=-x,

即|N-(y)|≥-x.又因为f是图G的一个符号边控制函数,满足任意一个顶点v∈N-(y),都有sy+sv≥0,所以有sv≥x>0.再根据V+的定义以及N-(y)⊆V+,有

(1)

容易得到,V-是个独立集.反证,若存在G上的一条边e=uv,且u,v∈V-,则su+sv<0,与f是图G的一个符号边控制函数矛盾.所以对于图G上的任意一条边e=ab∈E(G),至少存在一个端点满足a∈V+或者b∈V+.因为图G是一个无三角形图,所以显然导出子图G[V+]中也不存在三角形.由定理2,我们可以得到

从而有

即

(2)

由式子(1)和式子(2)可以得到以下式子,

(3)

故

(4)

所以结合式子(3)和式子(4)可得,

(5)

(6)

因为图G的顶点数为n,又由符号边控制数g(n)的定义,结合式子(6)可得