可靠度约束下摆线针轮减速器加工精度优化*

王少虎，宿月文，金守峰，李宇涛

(1.西安工程大学机电工程学院，西安 710048；2.宝鸡文理学院陕西省机器人关键零部件先进制造与评估省市共建重点实验室，宝鸡 721016)

0 引言

摆线针轮减速器具有高减速比、高传动效率、高承载能力且低噪音的优势，被广泛应用于工业机器人、机床，以及其他高精度传动领域[1]。该减速器的制造误差的控制对其传动性能有重要影响[2-3]。

国内外学者对摆线针轮传动精度分析主要从两个方面展开，一类是基于轮齿接触分析方法(tooth contact analysis，TCA)的研究；另一类是通过动力学建模和虚拟样机技术的系统仿真方法。其中，TCA分析方面，LITVIN等[4]基于齿轮啮合原理与坐标转换法，推导出考虑齿廓修形的摆线轮廓的参数式，进而建立完整的TCA分析流程，得到了摆线针轮减速器运转时的传动误差曲线。李轩[5]应用齿面接触分析原理，建立了有侧隙啮合摆线针轮啮合副TCA模型及LTCA(loaded tooth contact analysis)模型，计算摆线轮轮齿与针齿之间背隙角，得到了有/无负载时传动误差、啮合刚度等传动性能指标。李兵等[6]采用作用线增量法，得到多齿啮合下的摆线轮输出转角误差,在此基础上建立了传动误差分析模型。

动力学分析及虚拟样机技术方面，XU、吴鑫辉等[7-8]提出了考虑间隙及加工误差的摆线针轮虚拟样机模型，对多齿接触和啮合特性进行计算，通过实测验证了虚拟样机的可靠性；刘华明、WIKLO等[9-10]建立了RV减速器的刚柔耦合三维模型并导入ADAMS进行多体动力学仿真，仿真数据表明考虑加工误差时输出轴力矩波动情况与实验结果更为接近。但是虚拟样机仿真软件对于多齿接触模型计算效率略低[11]。任军、WANG等[12-13]采用集中质量法建立了十六自由度的重载RV减速器动力学模型，分析了整机固有频率对系统的转动惯量和刚度的灵敏度；杨伟朋[14]基于等价误差法建立RV减速器动力学模型，并将单个制造误差引入到动力学模型的传动误差计算中。

上述研究表明，已有的TCA方法研究较少考虑减速器的制造误差和设计参数优化。动力学仿真与虚拟样机技术存在比较难于融入多个制造误差和计算效率低的问题。因此，本文根据摆线针轮传动特点，建立了考虑齿廓修形、加工误差的轮齿接触分析法，以获取传动误差。然后针对各加工误差对传动误差的灵敏度进行分析，以传动可靠度为条件，利用DIRECT算法对修形量和加工误差进行优化，得到一组许用传动误差下制造成本最低且可靠度高的摆线针轮减速器加工参数。

1 综合齿廓修形和制造误差的摆线轮针齿建模

1.1 考虑修形的摆线针轮传动的几何模型

摆线针轮减速器的加工过程产生的制造误差会导致装配时零件之间产生干涉。通过对齿廓适当修形，可提升整机的装配性。常见的摆线轮齿廓修形方法有针齿半径修形、针齿位置修形和偏心量修形[15]。前两种方法较为常用，因此综合该两种修形方法，基于坐标转换原理，建立齿廓坐标系，可得到通用的摆线轮齿廓参数式。

图1所示为摆线轮齿廓坐标系示意图，其中Sf(Xf-Of-Yf)为固定坐标系，且Of为其原点；Sc(Xc-Oc-Yc)为摆线齿轮坐标系，Oc为其原点；Sp(Xp-Op-Yp)为针齿坐标系，Op为其原点。Oc与Of重合，Op与Of相距一个曲柄偏心量e。φc为Sc之转角，φp为Sp之转角，Rp为针齿中心到Op的距离，Rrp为针齿半径，M点为针齿与摆线轮接触的一点，α为M点在针齿上的角度参数。根据啮合原理，可将摆线轮与针齿视为一对啮合齿轮，则假定nc为摆线轮齿数，np为针齿数，二者转角和齿数符合式φcnc=φpnp。依据此关系式，并考虑针齿半径修形和位置修形，可得到摆线轮齿廓方程的参数式为rc=[xc,yc,1]T，其中：

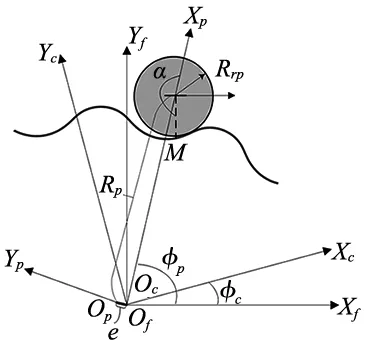
图1 摆线轮齿廓坐标系

(1)

(2)

式中，dR为移距修形量；dr为等距修形量，角度参数α可表示为：

(3)

在摆线齿轮参数式(1)～式(3)里，dR、dr与e为摆线轮齿廓修形参数，通过不同修形参数组合，可达到不同的修形效果。若专门针对修形参数，摆线轮齿廓参数式可简化为rc=rc(φp,dR,dr)。

1.2 考虑制造误差的摆线轮齿廓几何方程

摆线轮上的制造误差主要来自实际加工摆线轮中心与理论中心不同，从而引起的齿距变化，齿距是摆线轮沿节圆圆周上，自齿形上一点至相邻齿上对应点所量得的弧长Δb。在此将齿距误差记为Et，考虑齿距误差的摆线轮齿廓线示意图如图2所示。真实廓线与理论廓线节圆半径差值为Δρ，分析时可以将齿距误差换算成角度误差θc=Et/(Rp-Rrp)。

图2 考虑齿距误差的摆线轮齿廓线

考虑齿距误差时的摆线轮齿廓在其自身坐标系Sc下可表述为：

rc(φp;dR,dr;θc,Δρ)=M1(θc)rc(φp;dR,dr;Δρ)

(4)

式中，误差的转换矩阵为：

(5)

1.3 考虑制造误差的针齿几何方程

针齿在实际加工时会因为刀具磨损、加工面温度升高等原因而产生针齿半径发生变化，记为针齿半径误差Δr[16]。考虑半径误差的针齿外圆轮廓方程为：

(6)

减速器中针齿孔加工时，会由于加工精度的限制导致针齿孔中心位置距离组装坐标中心产生误差，从而形成针齿分布圆半径误差ΔR和针齿中心平面位置度误差。后者可定义为，实际针齿中心位于一个以理论中心为中心，半径为公差带的一个圆内。利用极坐标表示为，误差半径为Re，误差半径角度为θp，如图3所示，其中灰色阴影范围为实际针齿中心出现的位置。因此综合上述针齿制造误差，针齿在固定坐标系下实际针齿轮廓的位置方程如式(7)所示，i为针齿编号，Ap为两针齿夹角，β为针齿在固定坐标系中接触点的角度：

图3 针齿位置度误差示意图

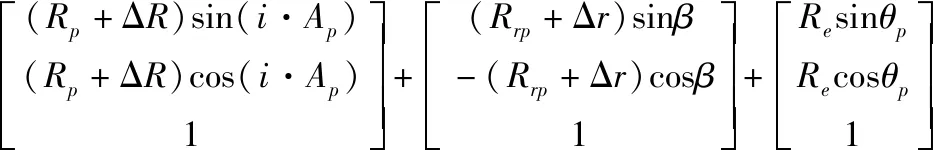
(7)

2 综合齿廓修形和制造误差的轮齿接接触分析

2.1 轮齿接触分析模型(TCA)

TCA分析中定义两个连续曲面接触时，其接触状态为共扼接触，其几何条件为：在同一坐标系下，两个连续曲面上的接触点位置坐标必须相同，且接触点上的外法向矢量也必须相等[17]。

设TCA模型中摆线针轮机构曲柄输入角为φ1，输出转角为φ2，摆线轮装配时曲柄偏心量误差Δe可作为偏心量e的附加值予以考虑，最终可得到固定坐标系下的摆线轮齿廓方程为：

rcf(φ1,φ2,φp;dR,dr;Δρ,θc,Δe)=
Mcf(φ1,φ2,Δe)rc(φp;dR,dr;Δρ,θc)

(8)

式中，Mcf为坐标转换矩阵，可表述为：

(9)

摆线轮齿廓上任一点的外法向矢量为：

(10)

固定坐标系下的外法向矢量为：

ncf=Lcfnc

(11)

式中，Lcf为摆线轮上法向矢量的转换矩阵：

(12)

同理，针齿的外法向矢量表述为：

(13)

根据共轭接触条件可得摆线轮齿廓与针齿的接触的数学表达式为：

(14)

式中，φ1为已知量，且给定各类制造误差时，未知量为φ2、φp、β。利用MATLAB软件求解该非线性方程组可得到3个未知变量数值解，进而确定具体接触点位置与实际输出转角。但是，若未知量的初值选取不当，将会造成求解无法收敛，所以需要确定合理的初始接触点参数。

2.2 TCA分析的初始接触点确定方法

为了在求解非线性方程时时稳定收敛，未知量φ2、φp、β的初值可通过瞬心法求解的理论接触点来获得[18]。给定φ1的情况下，φ2的理论初值为φ20=φ1/nc。图4中W点为速度瞬心，针齿和摆线轮的理论接触点B的法向矢量nc必须通过瞬时中心W。nc与+Xf轴夹角即为的β的初值β0。即：

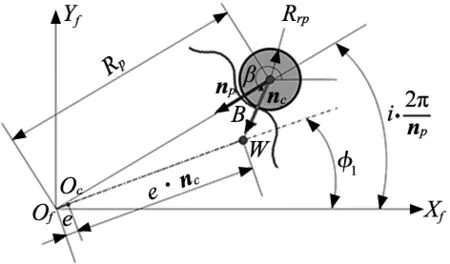
图4 瞬心法针齿理论接触位置

β0=tan-1(nc·x,nc·y)

(15)

进而由nc可推导出B点位置矢量为rB，并由几何位置关系得到针齿转角初值φp0，即：

rc(φp)=rB

(16)

2.3 轮齿接触分析计算传动误差

摆线针轮减速器的实际输出角可由前一节的TCA分析式求解所获得，即为求解后的φ2。传动误差为实际输出和理论输出值的差值，如式(17)所示。由于当摆线齿轮在运转时，会先将摆线齿轮转至和针齿接触，将起始间隙消除，所以会将运动误差平移一个角度，再计算其中最大值和最小值的差距，此值称为最大传动误差。

(17)

图5示出了用于计算传动误差的流程。首先确定摆线齿轮的修形轮廓参数式，针齿和摆线齿轮在固定坐标系中的位置和法线向量。再通过搜索φ2的最小值求解真实接触点，当输入角φ1大于最小输入角时，根据式(17)确定传动误差。最后再计算此输入角范围内的最大传动误差。

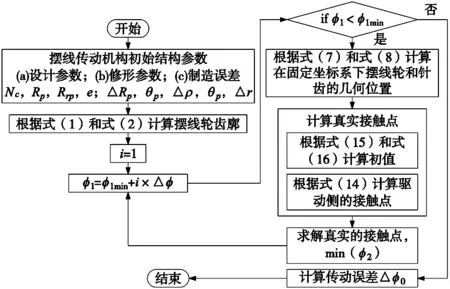
图5 摆线针轮机构传动误差计算流程

3 加工误差对传动精度的灵敏度分析

3.1 传动误差求解

根据上文提出的TCA模型，可在固定的摆线齿轮设计尺寸下，求解输入一周的传动误差变化。采用的摆线轮与针齿设计尺寸与修形量如表1所示。

表1 摆线针轮减速器结构参数

将设计参数代入模型求解，得到机构传动误差曲线如图6所示。图中可以看出，传动误差呈周期性的波形。

图6 传动误差曲线

3.2 加工误差的灵敏度分析

灵敏度分析的方法是将各加工误差作为变量分别加入齿面接触分析，观察最大传动误差结果的变化趋势[19]。

3.2.1 针齿半径灵敏度

设置针齿半径从7.9 mm逐步增大至8 mm，则图7为针齿半径变化对传动误差影响曲线图，图中点划线皆为线性拟合曲线，斜率即为灵敏度。可以观察到越小的针齿会造成越大的运动误差，近似呈线性关系。

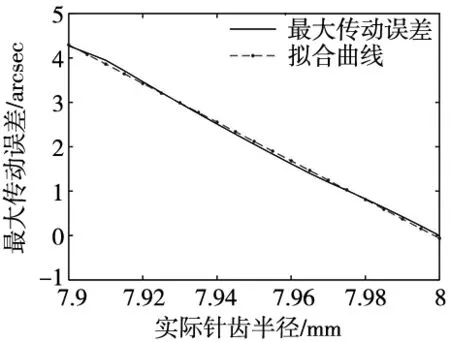
图7 针齿半径误差对传动误差灵敏度

3.2.2 针齿分布圆半径灵敏度

设置针齿分布圆半径从96 mm逐步增大至96.1 mm。图8为产生的实际针齿位置变化对传动误差影响曲线图，图中点划线皆为线性拟合曲线。可以观察到越远的针齿位置造成的传动误差越大，近似呈线性关系。

图8 针齿分布圆半径误差灵敏度

3.2.3 摆线轮齿距灵敏度

设置最大累加齿距从-0.02 mm逐步增大至0.02 mm。产生的传动误差对最大累加齿距变化如图9所示。可以观察到最大累加齿距绝对值越大，皆会造成越大的运动误差，造成的影响量近乎相等。

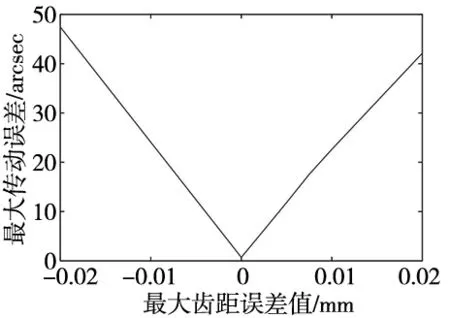
图9 最大累加齿距误差对传动误差灵敏度

3.2.4 曲柄偏心量灵敏度

设置实际曲柄偏心量从2.98 mm逐步增大至3.02 mm。图10为产生的运动误差对实际曲柄偏心之曲线图，可以观察到偏心量的实际值越大，运动误差越大，灵敏度也越大，且近似呈指数关系。

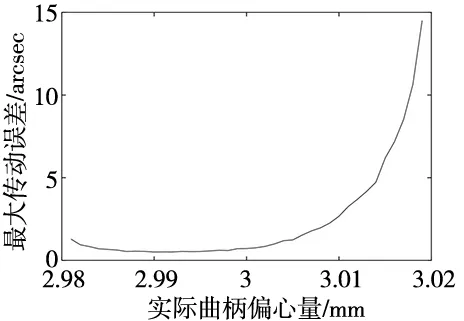
图10 曲柄偏心量误差对传动误差灵敏度

4 基于可靠度的加工误差优化与评估

4.1 加工误差优化

根据不同制造误差对传动误差灵敏度作为参考，可以在规定的传动误差条件下对修形量和加工精度进行优化，实现最低的制造成本。本文利用DIviding RECTangle(DIRECT)样本算法[20]，在传动误差限制范围内设定样本参数，利用有限的分割及变量搭配，逐渐逼近全域最佳解，以确定最优的摆线轮与针齿的加工精度和修形量。下文将最大运动误差的限制设为30 arcsec。算法中各变量定义如下：

(1)设计变量：制造误差与加工方式、加工刀具和生产环境等诸多因素有关，这些因素无法明确量化。因此，将所有的设计参数公差带上下限人为设定，如表2所示。

表2 设计变量的取值范围

(2)约束函数：基于可靠度的加工精度最优化过程中，设定分析的总样本数为Ns，若某组样本得到的传动误差超过了限制值，则认为该组样本不合格。假定不合格样本组数必须低于NfKE，则可接受最低可靠度表示Pc为：

(18)

(3)目标函数：摆线针轮减速器制造时，通常要求在满足规定传动误差的前提下，其制造成本越低越好。因此将目标函数设定为满足传动误差要求下，各个设计变量的公差带范围总和，将此目标函数最大化，则代表达到最低成本的最大公差带范围。公差带成本以(花费/mm)表示。此外，将各个参数之公差带范围前，再乘上一个权重值wi(0.1≤wi≤1)，表示各公差带对目标函数产生不同的影响。权重值越大，表示该参数所控制的公差带的成本越低，即增加该误差公差带范围对目标函数的影响较大。考虑各零件精度的成本控制，针齿权重取0.1，摆线轮权重取0.2，曲柄权重取0.3。程序在最佳化计算时，会根据权重而判断要提高何种设计参数公差带，而使结果满足传动误差条件下，又可达到成本最低的制造方式。优化出的最大公差带范围fo如式(19)所示，TZ表示各个制造误差公差带。

maxfo=(w1×A_Rrp_TZ+
w2×A_Rp_TZ+
w3×A_Re_TZ+w4×D_A_TZ+
w5×Max_cumulative_pitch_error_TZ+
w6×A_A_TZ)

(19)

在使用DIRECT算法对目标函数最佳化时，为使计算结果准确，应尽可能设置多的样本数迭代，所以在此将样本数分为100、500及1000做讨论。将产生出的样本数据带入计算TCA程序中，可求解所有样本的传动误差结果。3组样本优化的目标函数结果如表3所示，优化后该公差带下最优设计参数取值如表4所示。

表3 优化结果

表4 优化后的设计变量取值

4.2 最优加工误差的可靠度分析

由最佳化程序得到制造摆线针轮减速器最低成本的设计参数公差带后，验证该公差带下的减速器运动误差是否在要求的范围，再对优化后的加工参数进行可靠度分析，在此将验证的样本数设为2000，可以更逼近于实际加工情形。3组样本优化结果的可靠度如表5所示。

表5 优化结果的可靠度

由以上数据得知，优化样本数越大，则所得公差带之结果可靠度越高，迭代样本数1000时获得的可靠度皆在99.5%以上，符合高可靠度的特性。一般摆线齿轮减速机的造价很高，所以通过该方法可避免制造出过多传动性能不达标的减速器，从而大大节约制造成本。

5 结论

本文依据摆线针轮啮合原理，建立了考虑齿廓修形、加工误差的轮齿接触分析(TCA)法，通过此方法对各加工误差下传动误差的灵敏度进行分析。基于分析结果，设计出一种可靠度约束下的轮齿修形与加工精度优化方法。得出以下结论。

(1)对各类加工误差下摆线针轮减速器传动误差灵敏度分析表明：针齿半径误差和针齿分布圆半径误差与传动误差呈线性关系；曲柄偏心量误差与传动误差呈指数关系；最大齿距累积误差与传动误差近似呈对称分布关系。

(2)基于DIRECT样本算法，对摆线针轮减速器加工精度进行优化，得出3组满足传动误差条件的设计参数公差带。验证表明在迭代样本数1000时选取的设计参数可靠度可达最高并且制造成本最低。