滚动直线导轨温度场建模与分析*

庞如达，张耀满，王振起，史家顺

(东北大学机械工程与自动化学院，沈阳 110819)

0 引言

高速高精度数控机床在加工过程中，热变形引起的误差占机床总误差的40%～70%[1]。滚动直线导轨作为机床重要功能部件，对其热特性进行研究有利于提高数控机床的最终加工精度[2]。国内外关于滚动直线导轨热特性的研究主要在理论研究，仿真分析与实验研究几个方面。

在理论研究分析方面，TACHIYA等[3]提出了一种利用机床特定测点的温度变化来逼近机床热变形的方法，得到了热变形近似方程。YUN等[4]建立了导轨的温度场和热变形数学模型，并对其求解得出了摩擦热对变形及应力的影响规律。WAN等[5]提出了求解二维热传导问题的有限差分区域分解算法，通过求解验证了算法的稳定性和准确性。李宛珊等[6]提出一种在内节点采用显式算法，边界节点采用隐式算法的显-隐差分格式求解二维热传导问题。多数学者只针对导轨长度方向进行一维导热问题求解，有些学者为了求解导轨截面二维导热问题的数学表达式，将导轨截面简化成简单的矩形并对实际的边界条件作了适当调整。

在有限元仿真分析方面，WANG等[7]采用集总电容法建立了滚动直线导轨的热模型，分析表明垂直载荷、运行速度和转矩对滚动直线导轨温度变化有显著影响。ZOU等[8]建立了考虑内部热源和外部热波动影响的高精度工作台热力学仿真分析模型，预测了由温度变化引起的工作台热误差。ZHANG等[9]基于摩擦热模型对滚动直线导轨进行热结构耦合仿真分析，得到了热特性对力学性能的影响规律。MING等[10]建立了滚动直线导轨有限元模型，分析了影响热变形的主要因素，并提出了相应的误差补偿措施。ZOU等[11]基于预紧力、热变形和磨损等因素综合作用，建立了滚动直线导轨的接触刚度仿真模型，得到了接触刚度变化情况。目前多数研究，对简化的滚动直线导轨模型研究与实际情况有较大差异，建立的模型相对简单，难以准确描述滚动直线导轨的热特性。

在实验研究方面，LEE等[12]通过实验研究了滚动直线导轨的热变形随运行时间的变化规律，得到了导轨热变形对导轨运动精度和摩擦系数的影响规律。周怡帆等[13]运用能量守恒定律和导热的基本定律建立了滚动直线导轨的温升和热变形理论模型，通过实验得到滚动直线导轨各测量点的温升曲线及稳态温升值。

目前，尚未有研究对导轨截面瞬态温度场理论模型进行建立与求解，并通过仿真与实验验证。本文以HSR15A滚动直线导轨为研究对象，采用有限差分方法建立瞬态温度场模型，求解得到滚动直线导轨截面温度场及其变化规律；建立滚动直线导轨有限元热特性仿真分析模型，获得导轨稳态温度场；通过热特性实验，验证了建立的温度场理论模型和热特性仿真分析模型的准确性。

1 导轨截面温度场理论模型建立

1.1 导轨截面导热模型和参数计算

滚动直线导轨在运行过程中，滚珠与导轨滚道因摩擦产生大量热，由摩擦热引起的热流密度[2]如式(1)所示。

(1)

式中，q为热流密度；J为热功当量值为4.2 J/cal；a为接触椭圆长半轴的大小；L为导轨承载区的有效长度。

滚动直线导轨在工作的过程中，导轨表面与空气直接接触进行对流换热。根据对流换热的特征数方程式求解对流换热系数如式(2)所示。

(2)

式中，Nu为努塞尔数；l为特征长度；λ为导热系数。

导轨与空气直接接触，属于自然对流换热，努塞尔数可由自然对流换热的实验关联式[14]求得，如式(3)～式(5)所示。

Nu=C(GrPr)n

(3)

(4)

(5)

式中，Gr为格拉晓夫数；Pr为普朗特系数；α为体积膨胀系数；cp为定压比热容；C和指数n为常数根据对流换热面形状与位置和流体流态进行选取。

式(1)～ 式(5)用以确定滚动直线导轨在特定工况下的热力学参数。

采用有限差分法建立滚动直线导轨温度场理论分析模型的过程中，需要将导轨截面的圆弧滚道、倾斜边界和椭圆热源边界简化为阶梯形折线。在导轨滚道接触区域处施加椭圆热源，其余边界与空气发生热对流。导轨截面导热模型如图1所示。

图1 导轨截面导热模型

1.2 导轨截面各节点离散方程组建立

基于有限差分法和热边界条件，用离散节点的温度值表示导轨真实的温度场，将节点按照其位置分为内部节点和边界节点，并将这些节点组成离散方程组，通过矩阵运算进行求解。

(1)内节点离散方程的建立。采用有限差分法对有限离散节点组成的温度离散方程进行求解，滚动直线导轨内节点如图2所示。

图2 导轨内节点示意图 图3 边界上的节点示意图

对内节点(i,j)采用泰勒级数展开法来推导出差分表达式，忽略截断误差后得到温度在Y和Z方向的二阶偏导和差分表达式如式(6)所示。

(6)

将差分表达式转换成矩阵式如式(7)所示。

(7)

考虑到热源移动和几何边界条件周期性重复，采用周期性边界条件来调节系数矩阵，通过边界节点离散方程给定边界条件，为利于Ay和Az两个系数矩阵的结构形式，便于变换和编程求解，将其变成对称矩阵，得到温度在两个方向上的二阶偏导和的统一表达式如式(8)所示。

(8)

(2)边界节点离散方程的建立。通过边界条件确定边界上的节点离散方程，边界上的节点分布如图3所示。

根据能量守恒定律，得到边界上的平直节点E、外部角点ACDFO和内部角点B的对流边界节点温度表达式，分别如式(9)、式(10)和式(11)所示。

(9)

(10)

(11)

式中，q为热流密度；h为对流换热系数；Ta为空气温度。

通过所有节点的温度离散方程构建导轨截面节点温度的离散方程组，得到温度Tt的矩阵，代入导热微分方程，得到不同时刻的温度矩阵，如式(12)所示。

(12)

式中，a=k/(ρc)为热扩散率；Tt为t时刻的温度矩阵；Tt+1为(t+1)时刻的温度矩阵。

1.3 导轨截面温度场求解

为了获取滚动直线导轨各截面的温度场，编写程序对外载荷400 N，滑块以6 m/min速度运行时的导轨截面温度场进行求解。导轨的结构参数和由式(1)～式(5)确定的热力学参数如表1所示。

表1 导轨的物理参数

内节点温度通过编写A矩阵与之对应，边界节点温度通过边界条件进行确定，求解导轨导热微分方程，获得导轨截面不同时刻的温度场，最终获得导轨截面在稳态时的温度分布情况，求解流程如图4所示。

图4 导轨截面瞬态温度求解流程图

在750 s、1600 s和1850 s时输出导轨截面温度图像，求解得到导轨截面在相应时刻的温度场，如图5所示。

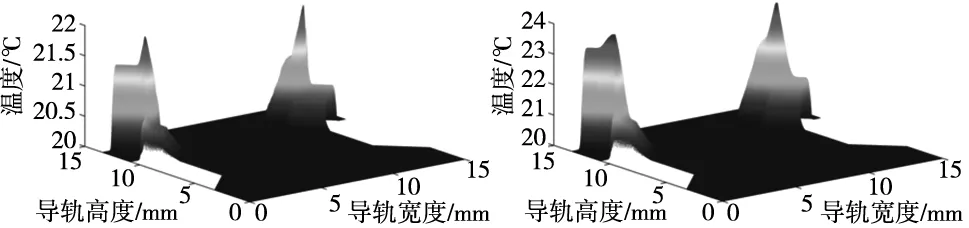
(a) 运行750 s后截面温度 (b) 运行1600 s截面温度

由图可知，导轨上滚道温度高于下滚道温度，热源区域的温升最大，随着时间的增加，导轨截面的热源区域的温度不断升高，且热源区域的热量不断向周围传导。随着运行时间的增加，温升速度越来越慢，最后达到稳定状态。导轨截面不同时刻最高温度具体数值如表2所示。

表2 导轨截面不同时刻温度

导轨截面稳态温度场如图6所示。由图可知，当导轨温度达到稳态时，导轨上滚道温度高于下滚道温度，导轨的最高温度为27.3 ℃，摩擦产生的热量主要影响导轨接触区域的温度变化。

图6 导轨截面稳态温度分布图 图7 导轨截面最高温度随时间变化

导轨截面最高温度随时间的变化如图7所示。滚动直线导轨在初始运行的1 h内，导轨的温升较快；之后温升逐渐缓慢，最终导轨温度达到稳定状态。

2 滚动直线导轨热特性仿真分析

环境温度设为20 ℃，导轨底部温度固定等于环境温度，当滑块滚动直线导轨在400 N垂直载荷的作用下以6 m/min速度运行时，依据表1对导轨中心区域滚道内外侧施加热流密度，对导轨不同区域分别施加对流换热系数。稳态热分析载荷与约束施加如图8所示。隐藏滑块后导轨的稳态温度场分布如图9所示。

图8 导轨稳态热分析载荷与约束施加 图9 导轨稳态热分析温度分布

由图可知，在导轨长度方向，距离导轨热源区域较近位置的温度均升高，离热源远的位置温度与环境温度相同；在导轨截面方向，温度呈对称分布，离滚道接触区域近的位置温度较高，离滚道接触区域远的位置温度较低。导轨在接触区域达到最高温度27.03 ℃。选取热源中心区域截面，得到导轨截面的温度分布，如图10所示。

图10 热源中心导轨截面稳态温度云图

由图6和图10可知，最高温度分别为27.03 ℃和27.3 ℃，最高温度相对误差为0.99%，理论建模求解结果与仿真分析结果一致。导轨截面靠近热源区域两侧和导轨顶端的温度分布不一致，主要是由于在进行导轨截面热特性理论分析时，对导轨结构进行了简化。

3 滚动直线导轨热特性实验

搭建实验台，如图11所示。将铂热电阻温度传感器粘在导轨滑块上，通过温度传感器测量导轨滑块的温度变化。其中，T1测量端盖的温度，T2测量滑块的温度，T3测量导轨端面的温度，T4测量周围环境的温度，同时通过数据记录仪采集并储存数据信息。

图11 实验台搭建

通过安装固定不同的负载板，对工作台分别施加13.5 N、27.0 N、40.5 N、54.0 N和67.5 N的负载，探究外载荷对导轨温度的影响，实验数据如图12所示。

根据实验数据可以计算出，载荷每增大13.5 N，滑块平均温升为0.2 ℃，导轨平均温升为0.21 ℃。将理论计算和仿真分析结果与实验数据进行对比，如表3所示。

表3 导轨在不同载荷下的最大温升及误差值

导轨在不同载荷下的最大温升的最大理论误差为7.25%，说明滚动直线导轨热特性模型正确；最大仿真误差为6.22%，说明热特性仿真分析合理。

通过改变滑块的运行速度测量导轨滑块的温度变化。滑块的运行速度分别为2、4、6、8和10 m/min，探究运行速度对导轨温度的影响，实验数据如图13所示。

根据实验数据可以计算出，速度每增大2 m/min，滑块平均温升为0.19 ℃，导轨平均温升为0.2 ℃。将理论计算和仿真分析结果与实验数据进行对比，如表4所示。

表4 导轨在不同速度下的最大温升及误差值

导轨在不同速度下的最大温升的最大理论误差为6.98%，说明滚动直线导轨热特性模型正确；最大仿真误差为4.19%，说明热特性仿真分析合理。

4 结论

热特性研究不仅有利于滚动直线导轨性能的优化，而且对热误差补偿具有重要意义。本文提出一种利用理论数学模型求解导轨截面瞬态温度场的方法，并通过仿真分析与实验得到验证。为利用数学理论模型分析滚动直线导轨热特性提供了参考，最终得出结论如下：

(1)对比建立的温度场理论模型与实验数据，稳态温度场理论模型和实验结果误差为3.99%～7.25%，且瞬态温度场的变化趋势与实验结果一致。

(2)滚动直线导轨温升速度随外载荷和运行速度的增加而增大，稳态时的温度也随着外载荷和运行速度的增加而升高。滚动直线导轨温度实验数据和仿真分析结果的误差为2.90%～6.22%，证明了有限元仿真分析模型的可靠性。

(3)滚动直线导轨在外载荷为400 N，运行速度为6 m/min的状况下运行时，导轨上滚道温度高于下滚道温度，稳态时最高温度的理论结果为27.3 ℃，有限元分析结果为27.03 ℃，温度随时间的变化符合热传导的规律。