改进差分算法的仿人控制器设计与参数优化*

李思宇，谭 飞,b

(四川轻化工大学a.人工智能四川省重点实验室；b.自动化与电子信息学院，自贡 643000)

0 引言

仿人智能控制(HSC)模拟人的控制智慧，将仿人思维控制方法与传统控制策略相结合[1]，是一种依据已有的先验知识决定对被控系统不同特征状态选择不同的控制策略的多模态控制技术[2]。在仿人智能控制发展过程中，许多固有缺陷并没有很好的解决，比如控制参数整定难问题[3-4]以及控制器的决策规则可靠性低等问题。控制器获得的控制效果与特征模型中特征状态的数量存在正比关系，但同时控制参数增加为控制器设计带来极大困难[5]。

仿人智能控制(HSC)器算法模型的建立是对系统获取的先验知识进行分析处理，对实现控制要求和控制行为过程的分析，是选定智能控制图式，建立控制模式映射的过程。这种映射通常有较多的参数，一般按经验设置，但难以获得最优的控制效果[6-7]。当前各种进化算法以及计算机硬件技术的发展，求解非解析多参数的优化，不需要目标函数的过多信息[8-10]，有基于Fuzzy-HSIC控制参数优化的混合算法[11]，陈家俊等[12]将伺服系统中的常用的手动整定PID改为机器学习以及模糊控制自适应整定，提升了参数整定效率。张芳等[13]设计了基于二阶线性自抗扰控制设计了电压源换流器高压直流输电换流站控制器，提升了系统动态性能以及鲁棒性。以上文献为解决控制器参数设置提供了有效可行的手段，但在仿人控制器中噪声对控制决策规则的影响依旧没有得到很好解决。

为改善上述问题，本文主要在HSC的决策过程，提出一种基于偏差em的仿人智能决策规则，在差分算法收敛速度慢，容易陷入局部最优的缺点下提出并采用行域可变差分进化算法(RVDE)研究HSC在不同对象上的参数优化设置问题，研究减小决策失误的控制策略。

1 行域可变差分进化算法(RVDE)

设算法的优化问题如式(1)：

z=minf(x)，x=(x1,x2,…,xm)∈S⊆Rm

(1)

式中，S为目标函数f(x)的可行域；xi∈[ai,bi]，i=1,2,…,m；ai,bi∈R，分别为xi的下界和上界；m为目标函数变量维数。

首先初始化种群{x1,…,xp}，种群的大小p一般取进制数加1～10倍目标函数变量数，如采用10进制浮点数，优化3个变量，种群可随机可取13～40个x个体构成初始矩阵X，矩阵每行为一个个体。对每个个体进行评价可得到矩阵Z。然后进行循环评价更新，直到得到规定评价次数或达到认可的收敛精度。算法有多种更新策略[14]，其中最常用DE/rand/1/bin策略，基于个体更新变异如式(2)所示，对式(2)同时更新矩阵Z。

(2)

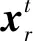
步骤1：计算式(2)，更新下一代个体。

步骤2：对于t+1代个体，更新可行域S如式(3)所示。

(3)

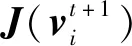
(4)

步骤3：根据经验值设定可行域规则如式(5)所示。

(5)

步骤4：之后更新的下一代与第i个个体进行交叉操作得到个体u，如式(6)所示。

(6)

式中，randj为[0,1]的均匀分布的随机数；C为给定的交叉概率，属于[0,1]；ri∈{1,2,3,…,p}的随机整数。然后得到的交叉个体进行评价如果更好就选择式(6)得到的新个体，否则原个体不变复制到下一代，如式(7)所示。

(7)

通过i从1～p取值，对改进变异策略和式(6)、式(7)的重复迭代应用，就可完成对目标函数(1)的全局最小值求解。

2 改进的HSC设计

对仿人智能控制系统进行设计[15]，仿人智能控制系统的结构如图1所示，R(S)为目标参数，GC(S)和Gp(S)为控制器和被控制对象的传递函数，E(S)为误差函数，U(S)为控制器输出，H(S)为系统反馈，Y(S)为优化后参数。

图1 闭环控制系统结构

一个有时延的对象在常规控制下的阶跃响应误差曲线如图2所示。

图2 系统误差曲线

分析图2，一个经验丰富的控制专家根据系统误差变化特征对系统进行操作控制，通常可以分为3种控制方式：Ⅰ加速控制，Ⅱ减速控制，Ⅲ等待观察。在等待观察的过程中，控制器需要给出个持续的激励，保证执行机构移动的适当的位置，使系统输出误差满足要求。这个持续的激励需要控制器对系统偏差的学习，采用设计积分器仿真与控制方式Ⅰ和Ⅱ中进行执行机构位置的学习。

系统的误差特征信息和决策可总结到表1。

表1 偏差特征信息与控制模式对照表

表中，“+”表示大于等于0，“-”表示小于0；Ⅰ、Ⅱ、Ⅲ分别表示3种控制模式。

根据控制决策方法[16]的基本方法和表1的信息特征，总结出一般HSC规则完成3种基本控制方式的决策算法。

(8)

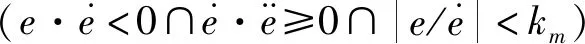
(9)

u=Ui(n)

(10)

(11)

U=kpkdde/dt+Ui(n)

(12)

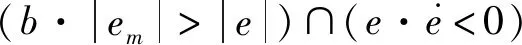
U=Ui(n)=Ui(n-1)+ΔUi(n-1)

(13)

此算法中的参数a、b是根据偏差大小的规则切换系数；e为系统当前实际偏差，em为当前方向(可能是正向或负向)当前时刻绝对值最大的偏差(偏差过0时em置0，然后重新实时求取)，em的计算方法为式(14)。图3的曲线实线部分给出了em的变化情况，虚线部分将保持虚线起始点值不变，如图中g点到h点实际系统误差如虚线部分，但em取值保持g点的值不变。若(e·em≥0∩|e|>|em|)∪e·em<0则

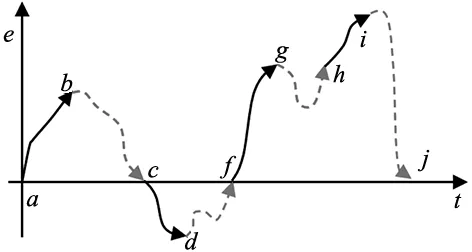
图3 偏差变化过程中em取值变化曲线

em=e

(14)

3 系统仿真与优化

根据对差分进化算法改进的一种有别于传统负荷模型的非仿真模型辨识模型[17]，设计仿人智能控制(HSC)算法kp、ki、kd、a、b等5个参数，其中a和b决定了规则成立的时间段长度，且要1≥a>b>0，这2个参数密切关联控制另外3个控制参数的大小，根据控制的特征，可先确定或者再优化更有利于合适的参数，使控制变量适应工业过程。

优化的控制目标选取很重要，希望系统快速且没有大的超调，设计的优化目标函数如式(15)所示。函数对超过2%的超调加以108惩罚。

(15)

式中，ts为控制系统的建立时间；t为时间变量；r(t)为系统的输入；y(t)为系统的输出；e(t)为系统的响应偏差。该目标函数是偏差绝对值时间加权积分指标(ITAE)的一种改进。

同时为说明仿人智能控制(HSC)的性能，把实际微分PID控制式(16)结果并与仿人智能控制(HSC)结果进行比较，算式中的微分增益在工业应用中不能过大，因此取为固定值10。

Gc(s)=kp[1+ki/s+kds/(kds/10+1)]

(16)

在进行优化时可根据ZN法或者通过仿真实验确定参数大致存在的范围，可使优化的效率提高。目标函数的求取需要用系统的仿真数据进行计算，仿真的步长及仿真的终止时间对算法计算效率影响很大。仿真步长一般取值以对象最小时间常数的1/20为参考，不宜过小，仿真终止时间以估计的最优状态下系统稳态无差为参考取值，不宜过长，否则计算量大，优化时间长。算法对控制参数的优化流程图如图4所示。

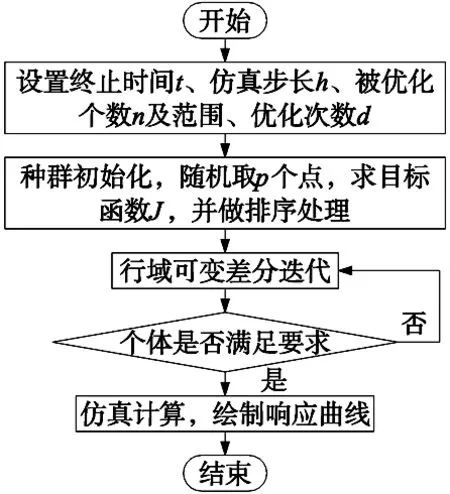
图4 控制参数优化流程图

4 优化实例

对象1：采用循环流化床锅炉的温床为对象[18]，其动力学特性具有大惯性特点，燃料的变化与床温可表示为式(17)。

(17)

该对象有3个极点一个零点，属于最小相位对象，仔细分析可发现系统纯比例控制是一个绝对稳定系统，因此可以用最大控制增益。设置种群数为30，最大评价次数5000，控制系统仿真步长0.025，仿真终止时间80，由于系统没时延，上升很快，改进仿人智能控制HSC的参数a取0.5，参数b的优化范围取(0.0001,0.5)，kp取最大范围(0,400)，ki取(0.0001,2)、kd取(0.0001,20)。另外现在超调用式(15)进行优化结果如PID1；不限制超调用普通的ITAE指标进行优化的见PID2，进行3次优化，最优结果统计如表2所示，它们的阶跃响应曲线如图5所示。从超调和调节时间来看，PID2的超调很大，PID1调节时间有点长，仿人智能控制(HSC)的调节时间只有20.3 s，超调量不超过1%，这个优秀结果比文献[19]所给的2466 s的调节时间有质的改善。

图5 Gp1对象控制系统的阶跃响应曲线 图6 Gp2对象控制系统的阶跃响应曲线

表2 对象Gp1控制系统的优化结果比较

对象2：采用有正零点的非最小相位对象如式(18)所示。仿真步长取0.005，仿真最大时间20 s，对于仿人智能控制算法，b先确为0.5，优化a的范围为(0.5001,1)，其他的参数取(0,5)进行优化，最大5000次评价，3次优化，最优结果如表3所示，相应的阶跃响应曲线如图6所示。表中还给出了基于临界ZN法整定的结果及文献[19]给的参数的仿真结果，相应的系统阶跃响应曲线对照可以看到，仿人智能控制的结果在快速和平稳性上表现是最优的。

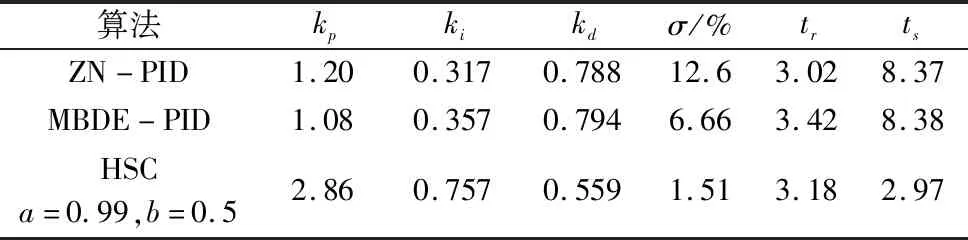
表3 对象Gp2控制系统优化参数及结果比

(18)

对象3：选用大滞后有时延的二阶对象如式(19)所示。设置仿真步长时间0.05 s，仿真终止时间300 s，b=0.5，对参数a的优化范围取值(0.5001,1)，其它控制参数取(0,100)对系统在式(15)下进行仿人智能控制(HSC)优化，其结果与文献[20-21]提供的粒子群优化的PID控制结果及ZN法整定的控制参数及结果如表4所示，相应的阶跃响应曲线如图7所示。仿人智能控制(HSC)的优化结果调节时间22.4 s，超调1.9%，与粒子群优化的PID控制(PSO-PID)相比有非常明显的优势。比较前面两种对象的控制效果，HSC算法在解决这种大滞后时延对象的控制，有更明显的优势，可以说是一种有效的提高大时延系统控制质量的解决方案。

图7 Gp3对象控制系统的阶跃响应曲线

表4 对象Gp3控制系统优化参数及结果对比

Gp3(s)=0.75e-8.1s/(1+61.4s)2

(19)

5 结论

本文通过对专家操作控制系统的分析，对仿人智能控制器做出了以下改进，第一分析了控制系统的误差变化信息，设计了两种仿人智能控制(HSC)控制器。第二对第一种控制规则在仿真和实践中的问题进行改进，提出基于误差分段决策的改进仿人智能控制规则。第三对差分进化算法的变异策略进行改进，采用行域可变差分进化算法针对三种不同的过程对象进行控制参数优化，并分析比较了它们在常规PID控制和优化PID控制的控制效果，算法在优化实例1～3的调节时间分别为20.3 s、2.97 s、22.4 s，在实例1～3中均为最优结果。实验结果表明改进仿人智能控制算法具有快速精确的寻优能力，也说明该算法在大时滞延迟系统的控制效果上表现良好。