考虑支护作用下的非圆形洞室应力流分布特征研究★
郑英豪,闫 鑫,李 冉,张 帅
(河北建筑工程学院土木工程学院,河北 张家口 075000)
地下深埋隧道的断面类型通常不再局限于圆形或矩形,取而代之的是马蹄形隧道,较传统圆形隧道而言,马蹄形隧道断面形式有着结构稳定、施工期对周边围岩扰动小,支护体系成熟等优点。然而隧道开挖产生的孔洞会对岩体的稳定性产生负面影响,进而可能诱发地下岩体结构的整体塌落。因此,对于了解非圆形含孔洞岩体的应力分布具有重要意义。
对于均质、各向同性深埋岩体中的隧道围岩应力的求解可视为平面应变问题,基于弹性力学理论通过求解实变函数可得圆孔、椭圆等简单孔洞的应力分布显式解[1-2],但当几何形状复杂时,复分析法具有了普适性的优势,因而被广泛运用于求解非圆形洞室应力解的问题[3]。Ukadgaonker等利用复变函数载平面应变条件下研究了三角形和矩形孔洞外的应力解析解[4]。
当洞室形状为复杂的非圆形孔洞时,对于映射函数的求解、应力边界条件式的确定将变得十分烦琐和复杂,这无疑大大增加了非圆形洞室围岩应力解析解求解的难度。而对于非圆形洞室映射函数的确定方法,国内外主要有Laurent级数法和Schwarz交替法等[5]。皇甫鹏鹏等[6]将映射函数系数展开为Laurent级数的形式,进行多次迭代计算,得到计算时间短、精度高的映射函数项数。王润富[7]利用复三角函数的正交性求解映射函数。吕爱钟[8]提出采用最优化解法,通过最优化技术来求解映射函数,其精度高,且适用性较强。
1 应力的复变函数表示
理论推导前,假定地下深部围岩体为均质、各向同性的线弹性材料。对于开挖深度远远大于洞室截面尺寸的岩体,可以考虑将空间问题简化为无限域内的平面应变模型。根据弹性力学理论,应力的求解最终归结为在给定应力边界条件下求解一个双调和函数U(x,y),即:
(1)
然而对于几何形状复杂、应力梯度较大、连通域多的应力问题时,双协调函数的求解十分困难。基于复变函数理论,在常体力条件下,双调和函数U(z)(z=x+iy)可表示为:
(2)

根据Muskhelishvili理论[9]与黎曼映射定理,z平面内极坐标系下各应力分量(σρ,σθ,τρθ)之间的关系可表示为:
(3)
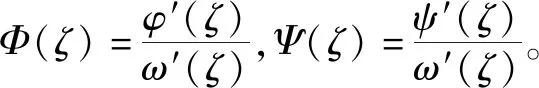
复应力函数φ(ζ)和Ψ(ζ)可表示为式(4)的形式:
(4)

无穷远处单值解析函数φ0(ζ)和Ψ0(ζ)可用Laurent级数表示如下:
(5)
孔洞需满足的边界条件式表示如下:
(6)
将式(4)代入式(6),并令ζ=σ,即可得到洞室边界上的应力平衡方程:
(7)
求解所需的应力函数φ(ζ)和ψ(ζ)的解析解可采用柯西积分或幂级数的方法求解。
2 映射函数表示
深埋隧道工程中孔洞的截面形状通常是不规则的,如图1所示。

以公路隧道规范中的双车道单心圆公路隧道为例[10],采用最优化方法[11],经过保角映射后,得到相应的映射函数形式如下:
ω(ζ)=R(ζ+c0+c1ζ-1+c2ζ-2+c3ζ-3+c4ζ-4+c5ζ-5)
(8)
其中,R=4.974,c0=0.015 5,c1=-0.12,c2=0.071 8,c3=-0.029 8,c4=0.002 4,c5=0.008 7。
3 结果与分析
3.1 应力分布规律
深埋隧道工程的大量地应力测量结果表明,地层中的水平应力一般情况下都大于竖向应力,且水平应力具有任意方向性,当洞室轴线方向与最大主应力方向平行时,洞室受水平应力的影响最小,有利于洞室整体的稳定性,当洞室轴线方向与最大主应力方向垂直时,洞室受水平应力的影响最大,洞室易发生失稳破坏,因此,研究不同侧压力水平下洞室周边围岩的应力及地层中应力分布规律对于地下深埋洞室支护结构针对性设计具有重要指导意义。
本节对围岩中不同位置处,不同侧压力水平下、不同支护力大小的环向应力、径向应力进行了分析,通过MATLAB数学计算软件,对计算得到不同距离处非圆形洞室应力分量,以研究应力沿洞室周边不同角度下的分布规律及地层中的应力传递规律。
3.1.1 径向应力分析
马蹄形洞室不同距离下的径向应力解析解分布曲线见图2。

由图2可以看出,随着侧压力系数λ由0增大到2,马蹄形洞室各角度下的径向压应力也逐渐增大,且径向压应力在马蹄形洞室拱脚处(对应角度约为120°)达到了峰值应力。当水平侧压力不存在(λ=0)或侧压力较大(λ=2)时,拱顶和拱底位置均处于受压状态,并随着侧压力系数的增大,压应力量值有小幅增大的趋势。随着距洞边距离的增大,径向应力也随之增大。当ρ=5时,围岩中径向应力值与远场应力值十分接近,当ρ=10时,围岩中径向应力值与远场应力值基本保持一致。
3.1.2 环向应力分析
马蹄形洞室不同距离下的环向应力解析解分布曲线,见图3,其中,ρ为ζ平面上点的半径。

由图3可以看出,当侧压力系数由0增大到2时,马蹄形洞室拱脚处附近应力集中程度逐渐增大,同时拱顶及拱底处的拉应力集中程度逐渐减小。从曲线整体形态上看,随着距离的增大,环向应力衰减较快,当ρ=3时,围岩应力与远场应力十分接近,当ρ=10时,围岩应力与远场应力基本保持一致。
3.2 不同支护力影响
通过将支护压力T引入式(6)即可考虑支护力对深埋洞室围岩应力的影响。考虑实际深埋工程中可提供的支护力大小在0.5 MPa以内,因此取支护压力T为0 MPa,0.1 MPa,0.2 MPa,0.3 MPa,0.4 MPa,0.5 MPa,其余参数与前文保持一致。马蹄形洞室内边界上环向应力分布见图4。

由图4可知:随着洞室内边界支护力的增加,马蹄形洞室边界上各角度下环向应力均有所减小,同时降低的幅度相同,且以拱脚处应力降低最多。例如,当支护力T由0增大至0.5时,拱顶处峰值应力由未支护状态下的1.67 MPa减小到支护下的1.34 MPa,减幅为19.8%。拱脚处峰值应力由未支护状态下的3.34 MPa减小到支护下的2.17 MPa,减幅为35.0%。可以看出,在洞室开挖的过程中,通过施加法向支护力,可以使隧道拱脚处应力集中现象也得到明显缓解。因此,在隧道开挖过程中,及时施作支护结构,以形成足够的支护力,将大大改善洞室周边围岩的应力集中现象。若在拱脚处增设锁脚锚杆,将提高拱脚部位的支护应力,从而进一步改善隧道拱脚周边围岩的应力分布。
3.3 应力流分布规律
通过对深埋洞室应力流分析可以得到围岩中力流密度大小,进而用于指导支护结构的施作,具体原理及相应计算公式见文献[12],围岩中应力流计算公式如式(9)所示:
(9)

当侧压力系数λ=0.5时,不同角度下应力及应力流沿距离变化规律见图5。

由图5可知:随着距洞边距离的增大,洞室周边围岩的径向应力、环向应力均有不同程度的减小,且逐渐趋于远场应力。随着角度的增大,在拱顶处(90°)径向应力流最大,而环向应力流最小。与之相反的是,拱肩处(0°)径向应力流最小,而环向应力流最大。同时,可以看出,随着距洞边距离的增大,环向及径向应力流距洞边一定范围内呈现非线性的关系,随着距离洞室边界的增大,呈现正相关的趋势。
4 结论
1)当水平侧压力不存在(λ=0)或侧压力较大(λ=2)时,拱顶和拱底位置均处于受压状态,并随着侧压力系数的增大,压应力量值有小幅增大的趋势。与环向应力变化趋势相反的是,随着距洞边距离的增大,径向应力也随之增大,但总体增幅较环向应力小,曲线变化规律与方形洞室变化规律一致。2)随着距洞室边界距离的增大,洞室周边围岩的径向应力、环向应力均有不同程度的减小,且逐渐趋于远场应力。随着角度的增大,在拱顶处(90°)径向应力流最大,而环向应力流最小。与之相反的是,拱肩处(0°)径向应力流最小,而环向应力流最大。环向及径向应力流距洞边一定范围内呈现非线性的关系,随着距离洞室边界的增大,呈现正相关的趋势。3)当支护力T由0增大至0.5时,拱顶处峰值应力由未支护状态下的1.67 MPa减小到支护下的1.34 MPa,减幅为19.8%。拱脚处峰值应力由未支护状态下的3.34 MPa减小到支护下的2.17 MPa,减幅为35.0%。