黄土洞室掘进深度与围岩位移变化规律研究
时卫民 王 鹏 赵尚毅
(1.32182部队,北京100043;2.重庆科技学院,重庆 404100)
0 引言
黄土地下洞室在开挖过程中,由于原有的力学平衡被打破,引起地应力的重分布。洞室顶部由于失去土体的支撑,在自重作用下会产生向下的位移,但由于受到两侧围岩的制约,围岩的应力会向两侧转移。洞室的侧壁由于失去侧向支撑,势必会在原有侧向压力的作用下发生向洞室内部的位移。洞室顶部和侧壁随着位移的逐渐增加,围岩的压力逐渐得到释放。在这个过程中,位移变形大,围岩压力释放就多,作用在支护上的压力就小,反之作用在支护上的压力就大。
地下洞室衬砌设计的关键是如何确定围岩压力释放率,要确定围岩压力释放率,就得了解洞室开挖过程中的位移变化规律,通过控制洞室开挖进度来控制位移,进而控制围岩压力释放率,使衬砌施工后受到的围岩压力符合设计的要求。关于围岩压力的释放,前人一般认为在开挖无支护情况下,黄土初衬前的围岩压力约为50%左右[1],离掌子面的距离超过洞室跨度1~1.5倍,掌子面的空间效应就消失[2]。
为了合理确定围岩压力的释放率问题,使确定的释放率能够与开挖进度相匹配,并且使衬砌施工后的围岩压力满足设计要求,本文以某黄土洞室为例,采用PLAXIS 2D/3D有限元分析软件,对某黄土洞室进行了二维、三维分步开挖、三维一次掘进等工况的有限元弹塑性分析,研究了不同工况下洞室位移的变化规律,为洞室围岩压力释放率确定提供了理论依据。
1 洞室掘进深度与位移的有限元分析
计算采用PLAXIS 2D/3D洞室分析软件,以某黄土洞室为例,洞室跨度为4 m,侧墙高度为1.5 m,拱顶为三心拱,拱高为1.333 m,洞室的计算简图见图1。
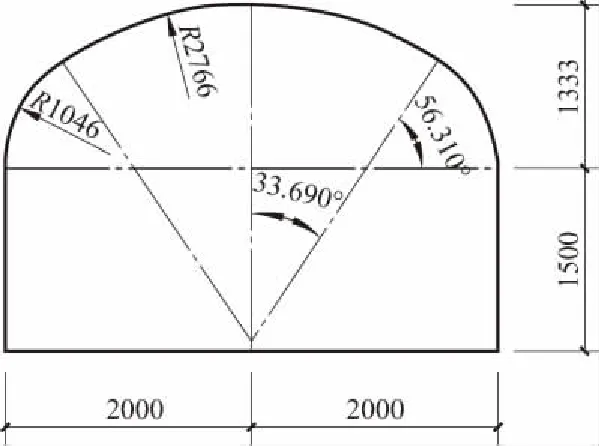
图1 洞室计算简图 (单位:mm)
1.1 计算模型
模型计算范围及边界:在x方向取洞室跨度的3.5倍(边界距洞边14 m),边界条件为水平约束;在y方向,洞室底部取洞室跨度的3倍(边界距洞室底部12 m),顶部分别按洞顶埋深10 m、20 m、30 m、40 m确定,下部为固定约束边界,顶部为自由边界;在z方向,取跨度的6倍(掘进深度取24 m),每2 m设置1个截面,边界条件为水平约束;洞室内部不考虑支护。计算按对称条件取一半建立计算模型,单元划分采用15节点的楔形体单元,材料模型采用摩尔库伦准则,洞室二维和三维单元网格划分见图2。

图2 有限元网格划分
1.2 计算参数
该算例采用老黄土的计算参数[3],岩土弹性模量E为4×104kN/m2,泊松比μ为0.35,重度为17 kN/m3,黏聚力c为50 kN/m2,内摩擦角φ为25°。
1.3 初始应力
初始地应力的施加采用PLAXIS软件中的K0加载过程[4],K0为侧向应力与竖向应力的比值,本文采用K0=1-sinφ生成初始应力场,其产生的初始位移在后续分步计算中置为0。
1.4 计算结果
模型建立后,采用二维和三维的分析方法,分别对埋深为10 m、20 m、30 m、40 m的工况进行有限元计算。图2中沿坐标轴方向为位移的正向。三维分析采用分步掘进法进行计算,每一步掘进的深度为2 m,如图3所示。各工况下,分步开挖的计算结果见表1—表4。
图3 分步开挖计算简图(埋深=10 m)
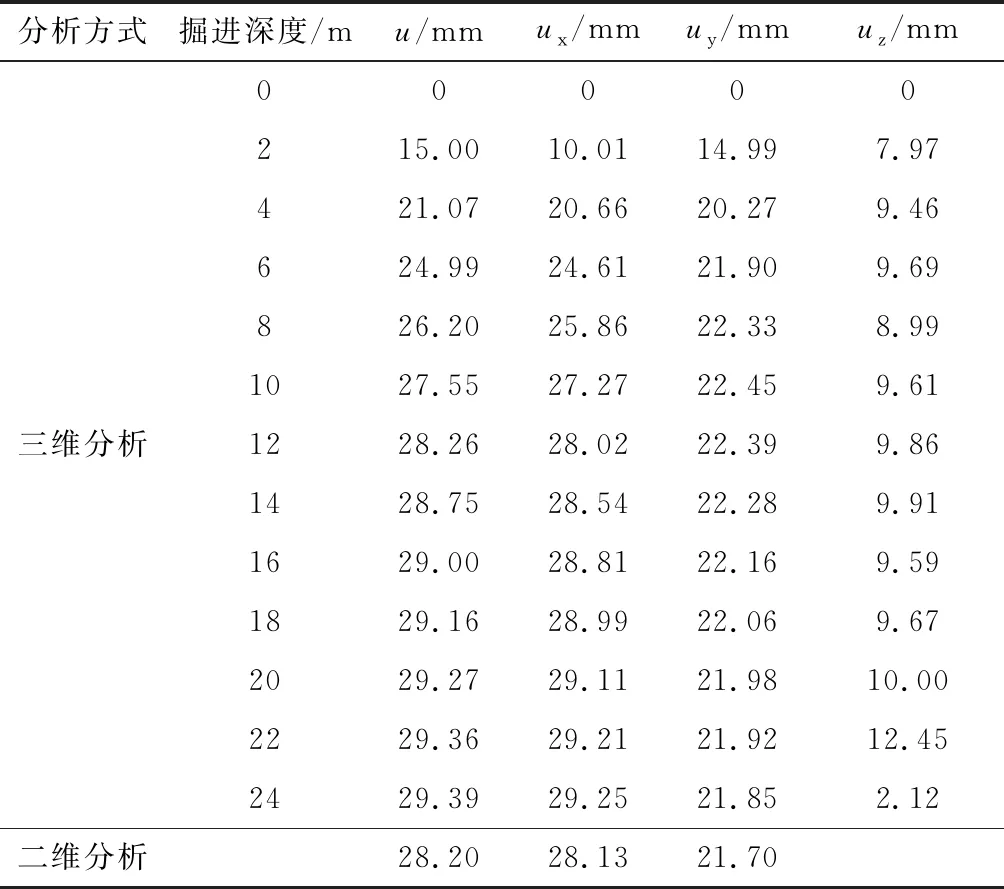
表1 埋深=10 m时分步掘进的位移计算结果
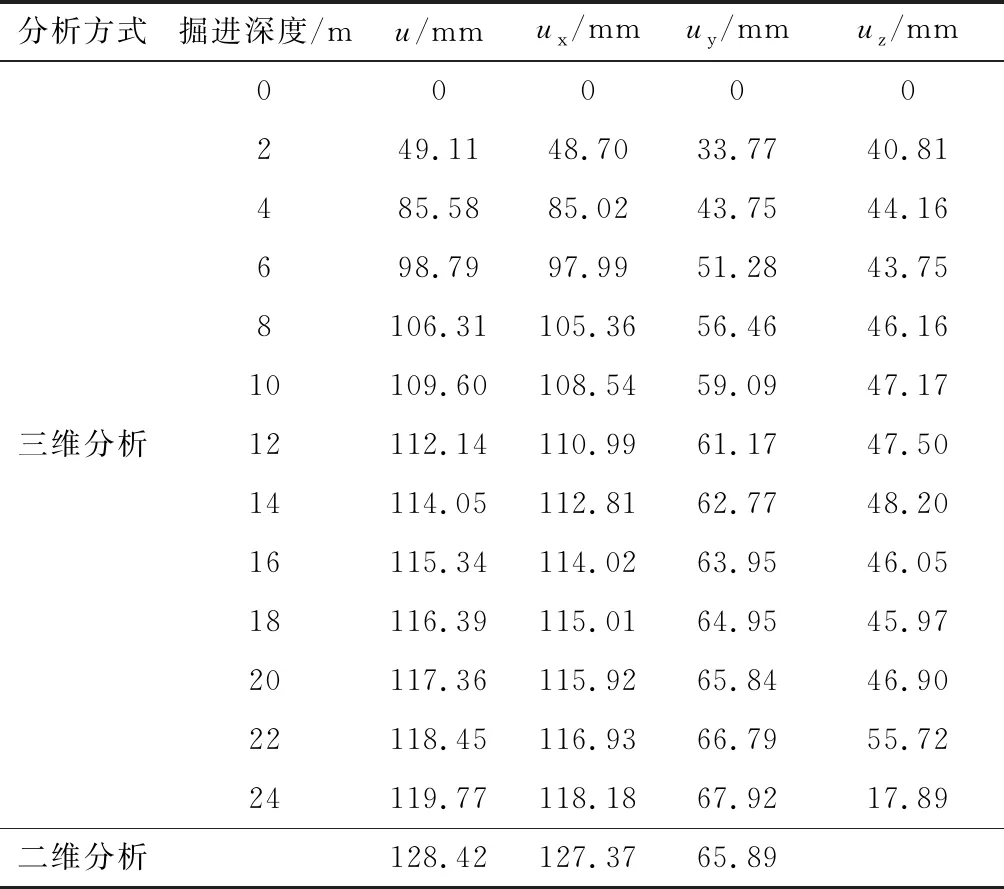
表2 埋深=20 m时分步掘进的位移计算结果

表3 埋深=30 m时分步掘进的位移计算结果
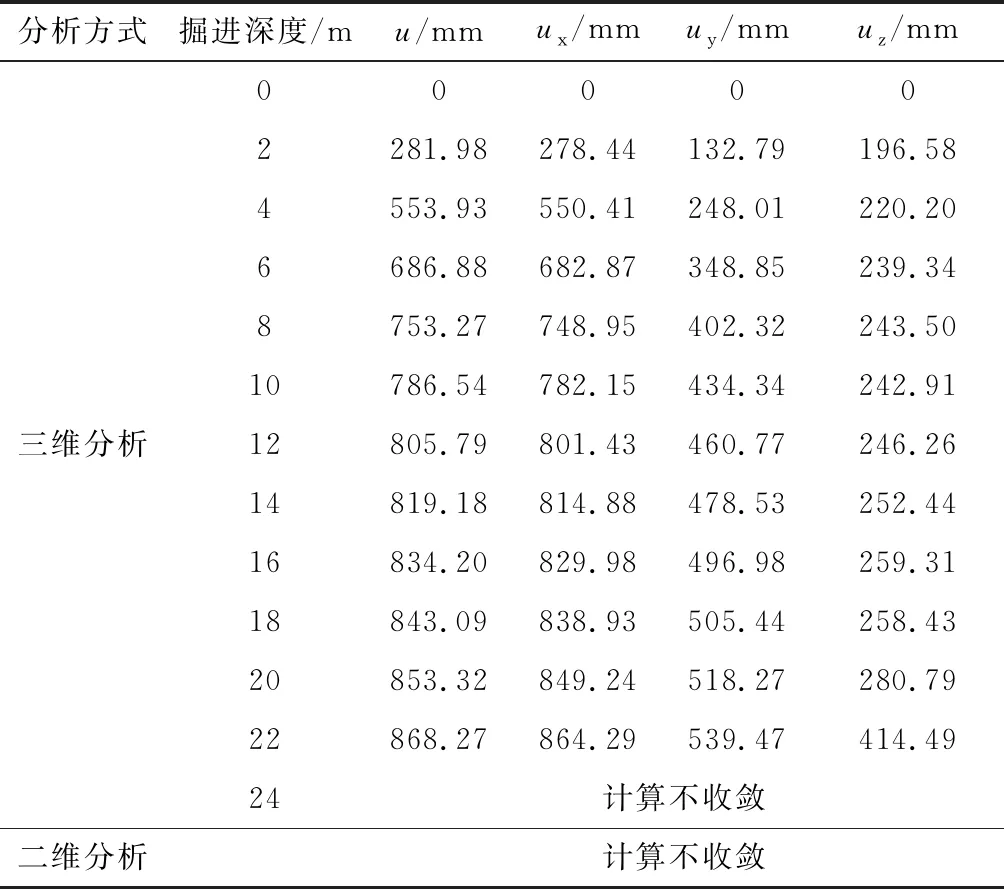
表4 埋深=40 m时分步掘进的位移计算结果
从分析曲线(见图4—图7)可以看出,当埋深小于10 m时,竖向位移比(位移与最终位移之比)大于水平位移比,说明竖向位移的变化大于水平位移,破坏将始于竖向坍塌。当埋深大于20 m时,水平位移比大于竖向位移比,说明水平位移的变化大于竖向位移,破坏将始于侧墙破坏。
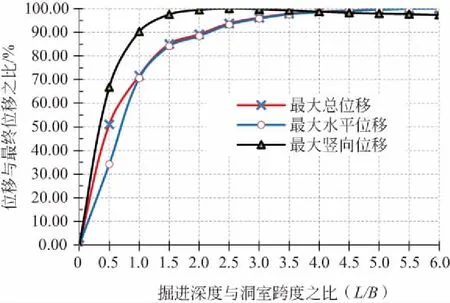
图4 掘进深度与位移的关系(埋深=10 m)
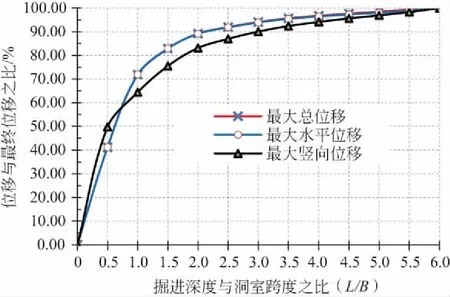
图5 掘进深度与位移的关系(埋深=20 m)
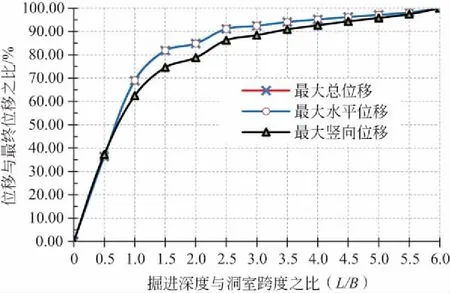
图6 掘进深度与位移的关系(埋深=30 m)
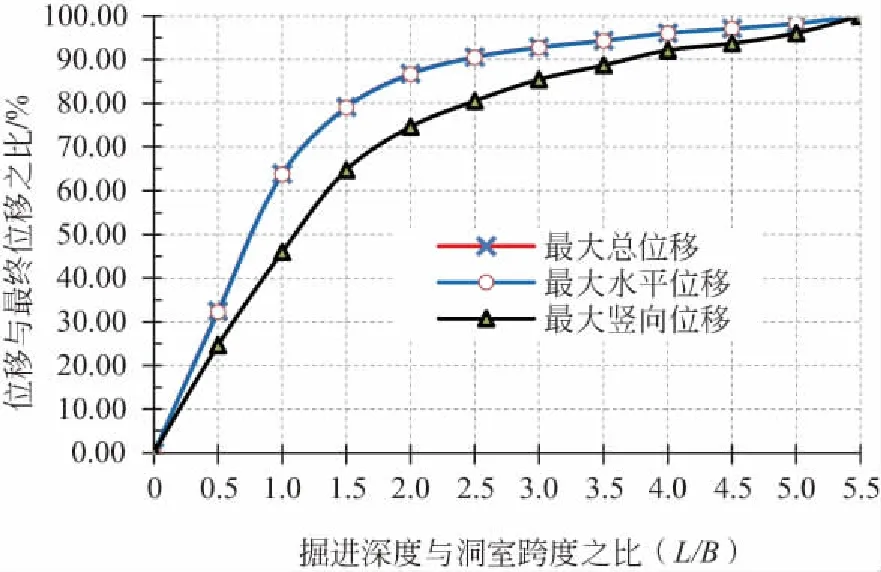
图7 掘进深度与位移的关系(埋深=40 m)
从二维和三维有限元分析的结果可以看出,二维计算的位移与三维计算的最终位移不完全相同,但很接近,因此可以用二维计算的结果来估算洞室开挖的最终位移。
1.5 结果分析
为了便于分析比较,把上述分析结果整理绘制在一张图中,见图8—图9。
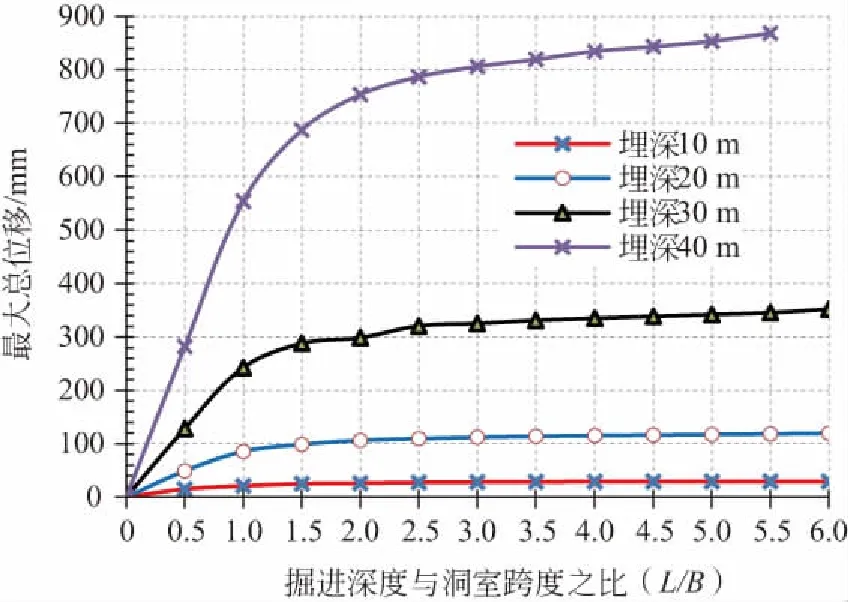
图8 掘进深度与最大总位移的关系

图9 掘进深度与位移比的关系
从图8可以看出,洞室的位移随掘进深度的增加呈抛物线性增加,埋深不同,洞室开挖时的位移差别很大,埋深浅时仅为10 mm左右,埋深大时约为900 mm,位移随埋深的增加呈非线性增加。
从图9可以看出,无论埋深多少,不同掘进深度的最大位移与最终位移的比值(位移比)变化曲线基本趋于一致,说明不同埋深的洞室在掘进时,其位移比的变化规律是一致的,掘进深度与位移比的分析结果见表5。

表5 掘进深度与位移比的计算结果
注:L为掘进深度,B为洞室跨度,括号中的数值为平均值。
从图9可以看出,当深跨比L/B<1时,位移比基本呈线性增加;当L/B>1时,位移比呈非线性增加;当L/B>3时,其最大位移基本接近最终位移。因此,为了防止掘进过程中位移过大引起洞室的坍塌,可以控制掘进的深度,使其位移满足稳定的要求,然后进行支护,待支护完成后,再继续进行掘进,以保证洞室开挖的稳定。
2 掌子面空间约束效应的有限元分析
洞室掘进过程中,由于受掌子面的约束,使掌子面附近的围岩位移不能立即全部释放,这种现象称为掌子面的空间效应[5]。前文采用分步开挖的方法分析了掘进深度与洞室最大位移的变化规律,本节采用前述同样的模型来分析掘进到某一深度时,掌子面附近洞室各部位的位移变化规律。图10为埋深为10 m时的有限元计算模型。

图10 掌子面空间效应计算模型(埋深=10 m)
2.1 计算结果
取埋深分别为10 m、20 m、30 m,分别按照一次掘进深度为14 m(一半开挖、一半未开挖)的情况进行三维弹塑性计算分析,然后分析拱顶、拱脚和底部中点的位移变化情况。埋深10 m、20 m、30 m时,计算的洞室最大总位移分别是24.6 mm、104.45 mm和269.99 mm。表6—表8分别为洞室顶部中点、拱脚、底部中点不同埋深情况下的计算结果。图11—图13分别为洞室顶部中点、拱脚、洞室底部中点在掌子面两侧的位移变化曲线。

表6 洞室顶部中点位移计算结果
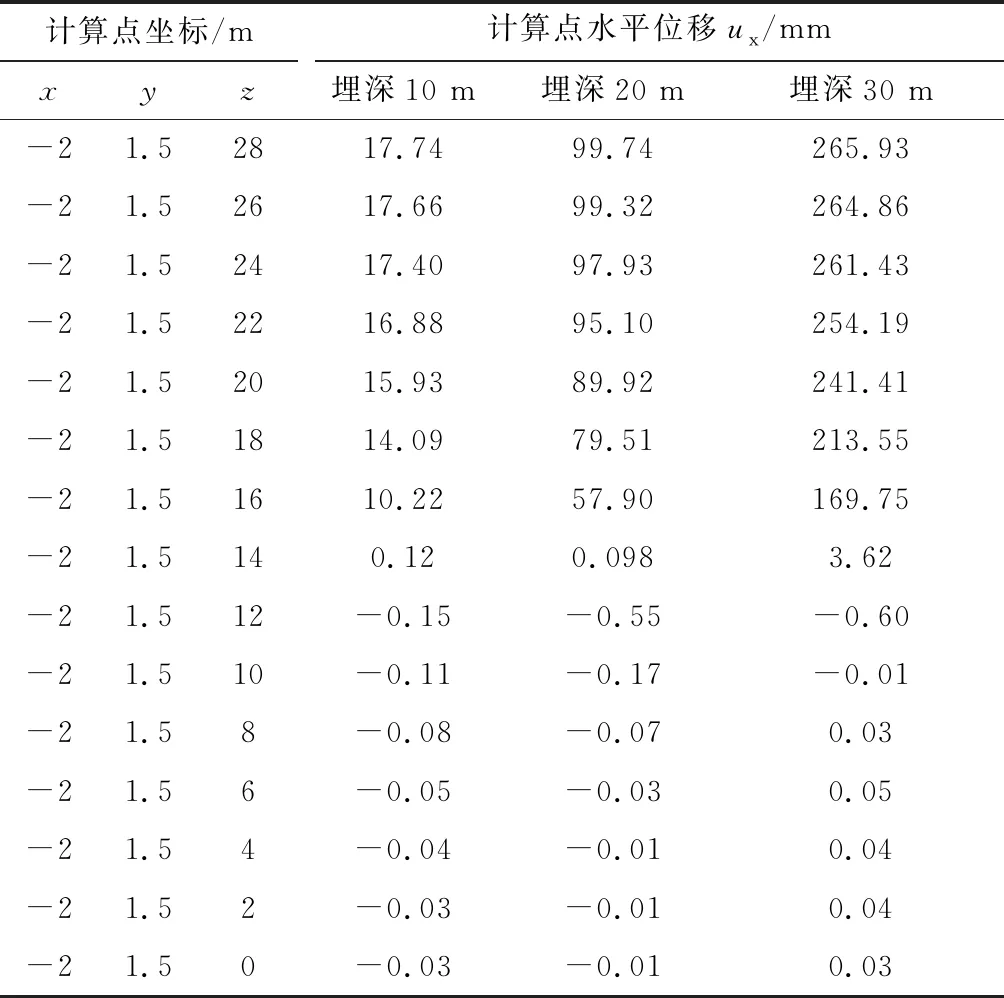
表7 洞室拱脚位移计算结果
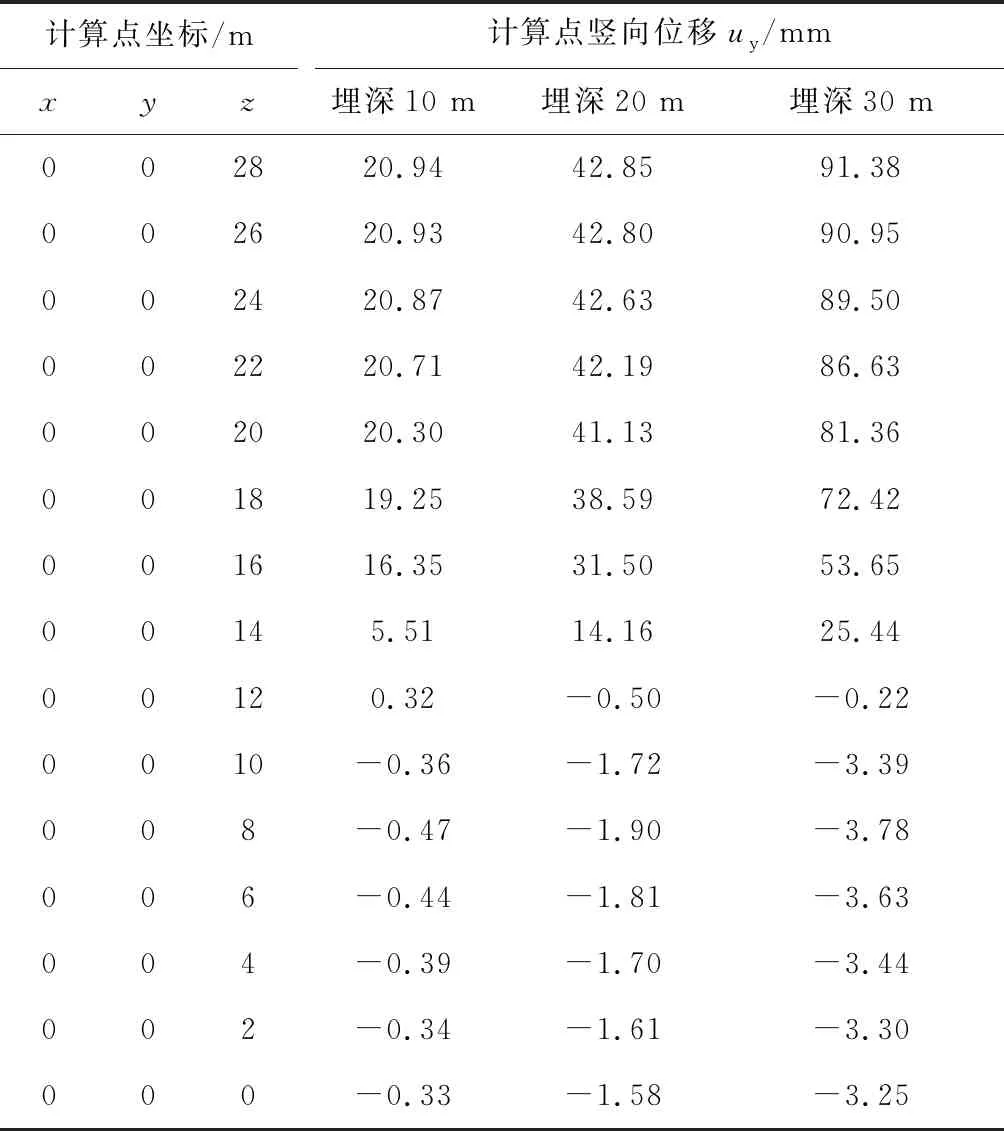
表8 洞室底部中点位移计算结果

图11 洞室顶部中点位移曲线

图12 洞室拱脚位移曲线
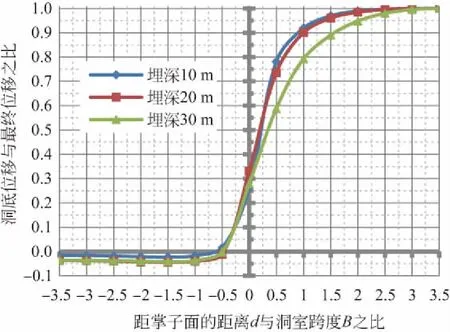
图13 洞室底部中点位移曲线
2.2 结果分析
从图11—图13可以看出,随埋深的增加,洞室顶部、底部各点的位移也随之增加,洞室顶、底部距跨比(d/B)与位移比的变化规律基本一致。计算的分析结果见表9。从表9可以看出,距离掌子面越近,其约束作用较强,距掌子面越远,其约束作用较弱。除拱脚处掌子面的水平位移几乎为0外,其它部位在掌子面处的位移为总位移的30%左右(占总位移的1/3左右),距0.5B时达到总位移的65%左右(占总位移的2/3左右),距2.5B时达到总位移的99%左右(基本达到了最终位移)。
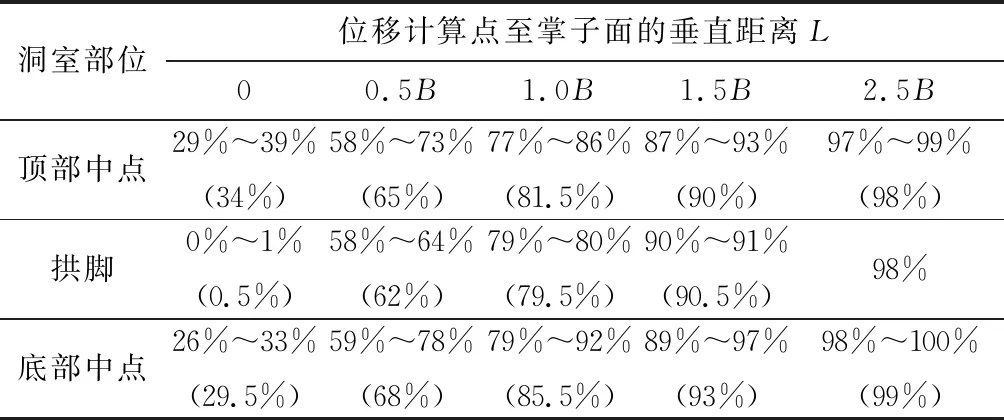
表9 不同掘进方式的位移计算结果
注:B为洞室跨度,括号中的数值为平均值。
将前面有限元二维分析、三维一次掘进至14 m和三维分步掘进至14 m时的最大总位移列入表10中。

表10 不同掘进方式计算的最大总位移
从表10的分析结果可以看出,三维一次掘进的位移计算结果比二维和三维分步掘进的结果要小一些,说明采用不同的有限元分析方案对洞室的分析结果是有影响的。因此有限元分析时,计算工况应与施工方案一致,这样模拟的结果才会更符合实际。同时可以看到二维分析和三维分步掘进分析的最大位移比较接近,因此可以用二维分析的结果来估算洞室的最终位移。
3 结论
通过对不同埋深洞室分步开挖和掌子面空间效应三维有限元数值模拟结果的分析可以得到如下结论:
(1)有限元二维计算的最大位移值与三维分步计算的最终位移基本一致,可以用二维的位移计算结果来估算洞室开挖的最终位移。施工时可以通过检测,获得开挖时围岩的位移值,将该值与二维数值分析的位移值相除,即可获得围岩的实际释放率。
(2)浅埋时,洞室竖向位移明显大于水平位移的变化,随着埋深的增加,洞室位移逐渐转变为水平位移大于竖向位移的变化,说明洞室浅埋时破坏始于洞室竖向的破坏,深埋时破坏始于侧墙的垮塌。
(3)不同埋深的洞室在掘进时,其位移比的变化规律基本一致,深跨比(掘进深度与跨度之比)为0.5时,洞室最大位移约为最终位移的42%;深跨比为1时,洞室最大位移约为最终位移的67%;深跨比为2时,洞室最大位移约为最终位移的88%;深跨比为3时,洞室最大位移约为最终位移的95%。
(4)掌子面空间效应的分析表明,距掌子面越近,其对围岩的约束作用越强,距掌子面越远,其对围岩的约束作用越弱。在掌子面处围岩的位移约为最终位移的1/3,距掌子面0.5倍跨度处的围岩位移约为最终位移的2/3,距掌子面2.5倍跨度处围岩位移基本达到了最终位移。
(5)洞室采用一次掘进和分步掘进的有限元分析方案,其位移计算结果是不一样的,分步开挖计算的结果要大于单步开挖的分析结果。因此有限元分析时,计算工况应与施工方案一致,这样模拟的结果才会更符合实际。

