关于隧洞围岩破坏特征的连续-离散耦合分析

刘绍兴， 任红磊

(河北工程大学 水利水电学院， 河北 邯郸 056038)

随着国民经济的不断增长，深埋洞室的稳定性问题屡见不鲜。埋深的增加意味着更加复杂的应力环境，因此有必要对洞室稳定性做针对性的研究。对于复杂应力环境下深埋隧洞破坏特征研究，目前主要集中在洞室围岩安全性评价、变形破坏机理及后期稳定性的把控等方面。研究方法主要包括室内岩石力学试验、现场监测及数值模拟等方面。

董书明等[1]通过有限元ANSYS对4种典型洞室断面开挖后的分析认为，蛋壳形隧洞最有利于洞室围岩稳定；李浩等[2]通过FLAC3D软件对4种典型断面进行研究后可知，圆形隧洞断面位移量、应力集中系数及塑性区面积均最小，曲墙式隧洞断面次之；皮进等[3]通过FLAC3D分析认为，从整体上看，圆形衬砌整体受力更均匀，而马蹄形衬砌可改善锚具槽部位的受力；米春荣等[4]认为在相同地应力条件下，巷道曲率的减小有助于减小巷道周边的破裂范围；项戈泽等[5]探讨了深埋地下洞室在自重应力条件下不同侧压系数对洞室岩爆过程及其洞室周围破坏区域的影响；谭涛等[6]发现当侧压系数大于1并逐渐增大时，塑性区在顶底板围岩拓展，两帮收缩程度明显增大；龚大银等[7]通过模拟不同侧压系数下的圆形巷道发现，随着侧压系数的增加，水平位移增加的现象越来越明显；袁本庆等[8]认为随着侧压系数的增加，巷道两帮围岩垂直应力呈递减状态，剪切应力、顶底板围岩垂直应力呈增大趋势；张振全等[9]通过工程勘测及数值模拟发现，侧压系数的增加会使应力集中区域由两侧向顶底板转移，进而导致深部巷道顶底板变形破坏；何富连等[10]在对底板冲击地压事故研究后发现，当侧压系数大于1.5时，底板塑性区范围急剧扩大，围岩稳定性急剧恶化。袁周祥等[11]利用PFC2D模拟了圆形与城门洞形洞室，认为侧压系数为2.0时，洞室周围发生岩爆的概率大大增加。蓝盛等[12]采用PFC2D建立煤体流固耦合模型,分析了侧压力系数对裂缝扩展及动能演化规律影响。

本文以齐热哈塔尔地区地质环境为背景，针对侧压系数和洞室断面形状，借助PFC6.0建立隧洞三维连续-离散模型进行研究，以期为地下洞室选形及稳定性问题提供指导。

1 连续-离散三维数值模型的建立

1.1 工程背景

齐热哈塔尔地处昆仑山脉高山峡谷地区，数以亿年的地质演化形成了该地区以片麻花岗岩为主的原岩地质条件。若在此开挖引水隧洞，则面临着高地应力、高地热、岩爆等一系列严重威胁施工安全的问题。因此，根据该地区的地质条件适当选取合适的断面形状减小开挖隧洞带来的风险及开挖后隧洞的稳定性就十分必要。

1.2 数值模型的建立

借助离散元软件PFC6.03D建立模型，如图1(a)所示，内部R-block模块尺寸为1 200 mm×1 200 mm×300 mm，外部zone模块尺寸为3 000 mm×3 000 mm×300 mm，其中模型的宽作为Y轴，长、高作为X、Z轴方向。Z轴方向为垂直应力，侧压系数为λ，X、Y轴方向为水平应力相等且均为λ倍的垂直应力。洞室断面形状分别为圆形、直墙圆拱形及正方形，具体断面尺寸如图1(b)所示。假设洞室周围岩体岩性单一且均匀分布，模型力学参数见表1。

图1 数值模型

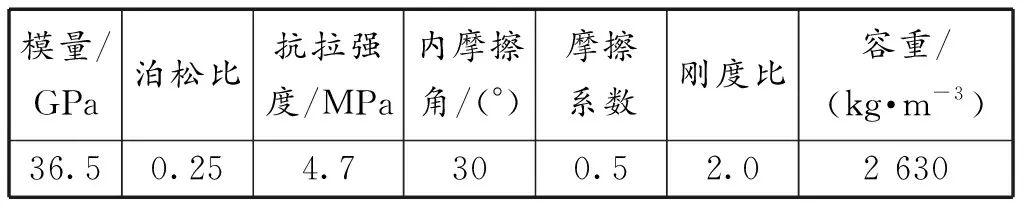
表1 模型力学参数

1.3 模拟方案

考虑侧压系数与洞室形状对隧洞破坏特征的影响，具体研究方案是：①侧压系数λ分别取0.5、1、2;②选取的洞室形状为圆形、直墙圆拱形和正方形;③根据洞室周围塑性区演化、洞室周围位移及洞室周边裂纹发育状态，对隧洞的破坏特征进行探讨。

2 结果分析

2.1 洞室周围塑性区演化

由图2～图4可见，3类洞室的塑性区演化随着侧压系数的变化呈现出了相似的变化规律。顶板处，塑性区域由两侧向中间上部拓展，破裂面积不断增大，这是由于水平应力的增加而造成的；而在两帮处，塑性区并未随着侧压系数的增大而出现明显的扩张现象，说明在3个不同断面形状的洞室中，λ的增大并不会造成洞室两帮塑性区域的拓展；底板处，破裂区域的演化与顶板类似，随着侧压系数的增大，破裂区域逐渐由两帮向中间及更深处发展，当λ=2.0时，破裂已经十分严重。在λ由0.5到2.0的变化中，原岩应力也由以垂直应力为主逐渐向以水平应力为主转化，具体表现为随着隧洞埋深的增加，水平应力不断增强，洞室围岩破裂程度更加严重。

图2 不同侧压系数下圆形洞室的破裂演化

图3 不同侧压系数下直墙圆拱形洞室的破裂演化

图4 不同侧压系数下正方形洞室的破裂演化

2.2 洞室周边位移

由图5、图6及图7可知，3类形状洞室开挖后，位移值较高区域随着侧压系数的增加而变化。当λ=0.5时，洞室两帮位移较大而顶底板位移较小；当λ=1时，洞室四周位移接近均匀分布的状态，且此种状态下洞室围岩稳定性最高；当λ=2时，洞室顶底板的位移已经高于两帮。分析以上结果，随着水平应力的不断增加，高位移区由洞室的两侧逐渐转移到洞室顶底板，λ=2时，位移增量明显增加。

图5 不同侧压系数下圆形洞室周围位移云图

图6 不同侧压系数下直墙圆拱形洞室周围位移云图

图7 不同侧压系数下正方形洞室周围位移云图

2.3 洞室周边的裂纹发育状态

如图8、图9及图10所示，当λ=0.5时，3类洞室顶板与底板均为拉剪复合破坏，两帮主要为张拉破坏；当λ=1时，洞室顶板与底板同样均为拉剪复合破坏，两帮以张拉破坏为主且剪切裂纹明显增多，但由图11可知，此时裂纹数量并未出现明显的增长，证明此时洞室周围岩体应力状态较为稳定；而当λ=2时，洞室的顶底板及两帮都呈现出拉剪复合破坏，且裂纹数量迅速增长，说明此时洞室周围岩体破损程度较为严重。

图8 不同侧压系数下圆形洞室周围裂纹发育情况

图9 不同侧压系数下直墙圆拱形洞室周围裂纹发育情况

图10 不同侧压系数下正方形洞室周围裂纹发育情况

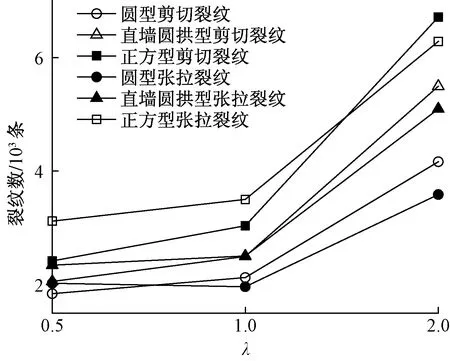
图11 不同工况下的裂纹数量

由裂纹的分布情况来看，洞室两帮的破裂程度是要小于顶板和底板的，λ=2.0时，裂纹迅速发育扩张，顶底板的破损十分严重，且λ一定时，圆形洞室破损程度最小，正方形洞室最大。λ=2.0时，圆形洞室的张拉裂纹数量为直墙圆拱形洞室的75.8%，为正方形洞室的62.07%，圆形洞室的剪切裂纹数量为直墙圆拱形洞室的70.4%，为正方形洞室的57.1%，说明当λ较大时，圆形洞室周围围岩破坏程度最小。

2.4 结果分析

对比以上结果发现，洞室断面形状一定时，随着侧压系数的增大，洞室顶底板塑性区变化明显，两帮次之。λ=0.5时，洞室两帮位移较为明显，λ=1时，洞室围岩位移分布较为均匀，此时的围岩稳定性也最高，当λ=2时，洞室的位移增量增加明显，且此时位移集中区已经转移到顶板。由洞室周边裂纹发育状态可知，洞室顶底板始终呈现出拉剪复合破坏，而洞室两帮则随着λ的增加逐渐由以张拉破坏为主转变为以拉剪混合破坏为主。λ一定时，圆形断面洞室相较于其他两种洞室塑性区面积，对围岩的扰动程度及洞室围岩破坏程度均最小。

3 结论

1)当洞室形状一定时，随着侧压系数的增加，洞室顶板与底板塑性区变化较为明显，两帮次之，随着λ的变化，洞室围岩高位移区由两帮转移至顶底板，且在λ=1时，围岩状态最为稳定。根据洞室围岩裂纹发育状态，洞室顶底板始终以拉剪复合破坏为主，而两帮则会随着λ的增大由张拉破坏向拉剪复合破坏转变。

2)当侧压系数λ一定时，圆形断面洞室无论是塑性区面积还是对围岩的应力扰动程度及围岩破坏程度均为最小。