轮腿可变式移动机器人的结构设计
谢 天, 张守京, 丁冬冬, 杨文彬
(西安工程大学 机电工程学院, 陕西 西安 710048)
移动机器人可以代替人类执行灾后搜救、军事侦察等特殊任务[1-4],特别是在危险复杂的工作环境中展现出极大的优势[5-7],这使得移动机器人的研究备受关注。
多运动复合式移动机器人的移动性能突出且环境适应能力强[8-10],典型代表有Yoshioka等[11]研制了一款轮腿混合式6足机器人,结合了轮式机器人的稳定性和机动性与腿式机器人的爬障能力。Ding等[12]提出了一种机动性强的轮式移动机器人,可实现平地行走和垂直爬行。Altendorfer等[13]设计了一种新型仿生6足机器人,可以完成行走和奔跑的工作,具有极高的机动性与稳定性。Bai等[14]基于折纸机构设计了一种新型的轮腿可变形移动机器人,可根据地形主动触发模式变换,实现平地行走和崎岖地形越障。Wu等[15]提出了一种新型的8足机器人移动平台,机器人具有行走模式和爬行模式2种工作形态,能够更好地适应非结构化地形。Birglen等[16]设计了一款新型4足步行机器人,可以高效稳定地攀爬楼梯台阶等复杂地形。Chen等[17]提出了一种具有转换机构的轮腿式4足机器人,可以克服室内环境中遇到的各种尺寸的台阶和楼梯。李智卿等[18]提出了一种对地形适应能力较强的轮履混合移动机器人,在面对复杂多变地形时可通过模式变换完成作业任务。甄伟鲲等[19]研制了一种具有可变形腰部的4足机器人,可以实现摆动直线行走和原地转弯,在面对极端地形时具有较强的适应性。郑辉等[20]提出了一种轮腿式爬行机器人的设计方案,机器人具有爬行和滚动行走2种工作模式。以上所提及的机构都显著提高了移动机器人的越障能力,伴随着越障能力以及地形适应性的提高,机器人运动效率低下、运动稳定性差等一系列问题也亟待解决。
课题组提出一种轮腿可变式移动机器人的设计方案,可以通过变径机构实现轮式与轮腿式的切换,使其既具备了轮式机器人机动性强,运动平稳的特点,也同时具备了腿式机器人越障性强的特点。
1 移动机器人的机械结构设计
1.1 整体结构设计
轮腿可变式移动机器人的总体结构如图1所示,车身为矩形,搭载有直流伺服电机,整机由2个直流电机负责提供动力(包括差速转向和行进功能),由另外2个电机负责变径轮的变径功能,驱动和变径独立进行,互不干涉,互不影响。如图1所示,机构整体呈对称状态,具备轮式和轮腿式2种工作模式。变径机构在电机作用下完成模式切换过程,使机构针对不同地形环境实现行走、转向和越障等功能。
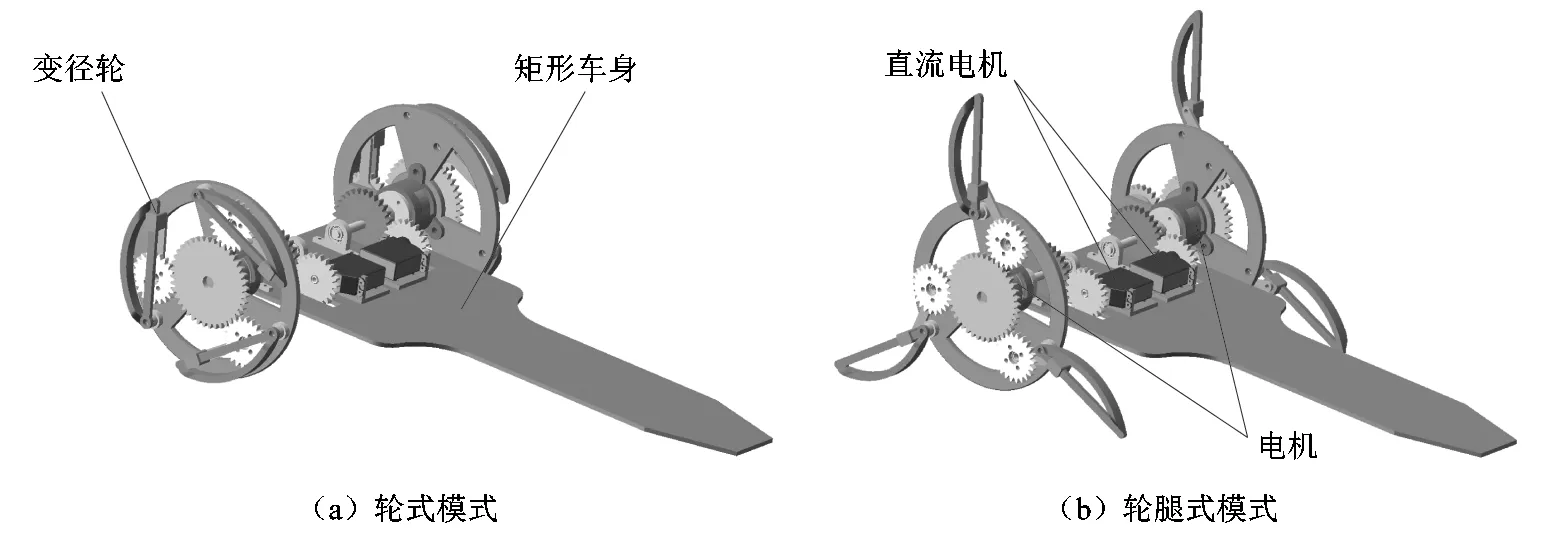
图1 轮腿可变式移动机器人3D模型Figure 1 3D model of wheel-legged variable mobile robot
如图2所示,该变径机构包含3组相同的弧形腿。轮式模式时弧形腿与滑块附着于轮毂内,适用于平整单一的地形环境;轮腿式模式时,在电机的作用下圆轮上的弧形腿伸展开来转换为3辐条状,适用于非结构化的复杂地形。r,r′分别为2种工作模式下的车轮半径。弧形腿上附着有橡胶,增大了车轮与地面的摩擦,提高了运动平稳性。

图2 变径轮结构示意图Figure 2 Schematic diagram of variable diameter wheel structure
机器人处于平整单一的地形环境时,在直流电机的作用下以轮式模式进行运动;机器人处于复杂多变的地形环境时,电机带动变形齿轮转动,使曲柄旋转最终将变形力传递到弧形腿上,机器人由轮式模式切换为轮腿式模式。移动机器人在变径机构的作用下可以根据不同的地形环境自由地切换工作模式,从而使得机器人的环境适应能力得到提高。
1.2 自由度分析
自由度主要是用来判断机构有无确定的运动,或者是有无唯一的运动轨迹。变径轮由3组相同的平面连杆机构组成,由修正的Kutzbach- Grubler准则,自由度
F=3N-2Pl-Ph。
(1)
式中:F为自由度,N为活动构件数,Pl为低副数,Ph为高副数。
由公式(1)可求得,该机构的自由度为1,所以该变径轮机构可以完成唯一且确定的运动,即轮式模式和轮腿式模式的变换动作。
2 运动学分析
当机器人处于平坦路面上会采用轮式模式行进,此时机器人具备轮式移动机器人高效的运动性能。在这种情况下,以传统轮式机器人的分析方法为基础,将机器人运动模型置于二维平面上,对机器人的运动学模型进行求解,可得可变径轮腿式机器人在轮式模式下的运动规律。


图3 机器人的运动学模型Figure 3 Kinematic model of robot
2.1 机器人正运动学
对移动机器人整机状态下的运动学分析时,可将其看作一个整体的刚性构件,移动机器人的运动学方程为:
(2)
求解式(2)可得:
(3)
在同一瞬时时刻时移动机器人车身上任何一点的角速度是相等的,所以其Q点的瞬时角速度为:
ωQ=(V2-V1)/T。
(4)
可求得移动机器人左、右轮的瞬时角速度分别为:
(5)
联立式(4)和式(5)可得移动机器人的转弯半径为:
(6)
又因为移动机器人中点Q在X和Y方向的线速度可以表示为:
(7)
联立式(3)和式(7)可得在大地坐标系下轮式模式移动机器人整体的运动学模型为:
(8)
轮式模式下移动机器人在任意时刻的位姿及运动状态可以采用微分法进行描述,可表示为:
p′=J(p)q′。
(9)
(10)
式中:p′为机器人速度,J(p)为机器人运动学雅可比矩阵,q′为机器人线速度。
2.2 机器人逆运动学
根据方程(9),q′的解为:
q′=J(p)-p′。
(11)
式中,J(p)-为J(p)的广义逆矩阵。
根据式(7)可知:
(12)
联立式(2)和式(12)能够得到:
(13)
(14)
以非线性方程组的形式表示式(13)和(14)可以记作:
(15)
或:
q′=J(p)-p′。
(16)
式(16)中:
(17)
式(16)即为移动机器人的逆运动学表达式,为实现机器人运动与位姿的稳定控制提供了理论依据。
由此可知移动机器人的运动状态和轨迹由ω1,ω2所影响决定,所以可以采用差速驱动的方案,实现其直线运动、圆弧运动和旋转运动。根据式(2)、式(3)、和式(5)可以看出运动状态的3种情况分别为:
1) 当V1=V2时,即在Δt时间间隔内移动机器人Q点的速度VQ=V1=V2,Q点瞬时角速度为0,移动机器人此时做直线运动;
2) 当V1=-V2时,即在Δt时间间隔内移动机器人的左、右轮做速度相等的反向旋转,转弯半径L=0,移动机器人实现绕Q点做旋转运动;
3) 当|V1|≠|V2|时,即在Δt时间间隔内移动机器人的左、右轮速度不相等,此时移动机器人实现绕Q点做半径相等的圆弧运动。
3 动力学分析
由式(7)化简可知移动机器人所受到的运动学约束方程为:
x′sinΨ-y′cosΨ=0。
(18)
该约束方程为非完整约束,是移动机器人的非完整约束系统。
以Q为参考点进行分析,移动机器人的位姿p和移动机器人的速度p′分别为:
p=[xQyQΨQ]T;
(19)
(20)
由式(18)整理可得移动机器人非完整约束为:
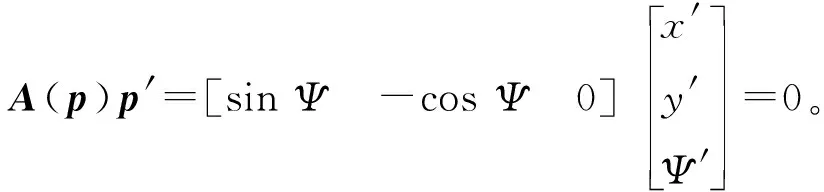
(21)
式中A(p)为运动约束方程中机器人速度的系数矩阵。
通过拉格朗日法对机器人整机的动力学模型进行求解,其具体的函数是总动能Ek和总势能Ep做差:
L=Ek-Ep。
(22)
则其拉格朗日方程为:
(23)
式中:FQ为相应于点Q的广义力,M(p)为约束力,λ为附加约束力,为了保证机器人2个移动轮不会产生侧滑特意再加1个λ。
因为该移动机器人仅在平坦路面上运动,所以其势能Ep始终为一个常数,可以将其记作C。另外可以将移动机器人的转动惯量不予考虑,则该移动机器人整机的拉格朗日函数可表示为:
(24)
式中:m为机器人的质量,IQ为绕Q点的转动惯量。
移动机器人整机在坐标系Q点处的广义等效力向量为:
(25)
式中:τ1和τ2分别为移动机器人左轮和右轮的驱动力矩,l为2轮间距。
根据拉格朗日方程,联立式(21)和式(25)可以求得移动机器人系统的动力学模型为:
(26)
由式(26)可得:
(27)
对式(23)求导,再联立式(27)可得约束力λ为:
(28)
具有n维广义坐标p的移动机器人整机在非完整约束条件下,由非完整约束的广义力学系统来描述,其表达式为:
B(p)p″+D(p,p′)p′+G(p)+MT(p)λ=Eτ。
(29)
式中:B(p)为系统正定惯性矩阵,D(p,p′)p′为系统与位置和速度有关的离心力和哥氏向心力矩阵,G(p)为重力矢量,τ为不考虑摩擦时左右2轮施加的合力矩,E为非奇异变换矩阵。
移动机器人在水平面运动时将其他对系统有影响的因素全部忽略不及,即有重力、摩擦阻力等因素,所以D(p,p′)p′与G(p)项都等于0,则式(29)可以简化为:
B(p)p″+MT(p)λ=Eτ。
(30)
其中
(31)
所以式(30)即为以Q为参考点移动机器人的无约束动力学模型。
4 基于ADAMS的运动仿真
4.1 机器人平坦地面直行运动仿真
如图4所示,为移动机器人平坦地面直行过程质心位移曲线图,从图中可以看出越障机器人在X方向上直线行进了约1.335 m,而在Y和Z这2个方向上基本没有发生位移,即在运动过程中其质心基本未发生左右偏移的现象。既验证了移动机器人处于轮式模式时理论模型和结构设计的正确性与合理性,也反映了当移动机器人以轮式模式直线运动时具有较好的稳定性。
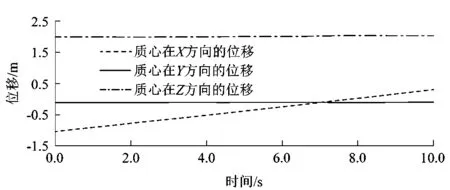
图4 移动机器人直线运动过程质心位移曲线Figure 4 Centroid displacement curves of mobile robot in linear motion
4.2 机器人“S”型转向运动仿真
移动机器人平坦地面“S”型转向运动过程主要分为2个阶段。第1阶段如图5(a)所示,在0~5 s时,左车轮线速度小于右车轮线速度,移动机器人以一定的半径进行右转运动,此时移动机器人也以一定的位移量向前方移动。第2阶段如图5(b)所示,此时左车轮线速度大于右车轮线速度,机器人则以相同的转弯半径进行左转运动,同时机器人依旧以一定的位移量向前方移动。且图中曲线光滑,波动较小,体现了移动机器人在做“S”型转向运动时稳定性较好,进一步反映了移动机器人结构设计的正确性与合理性以及其运动的灵活性。
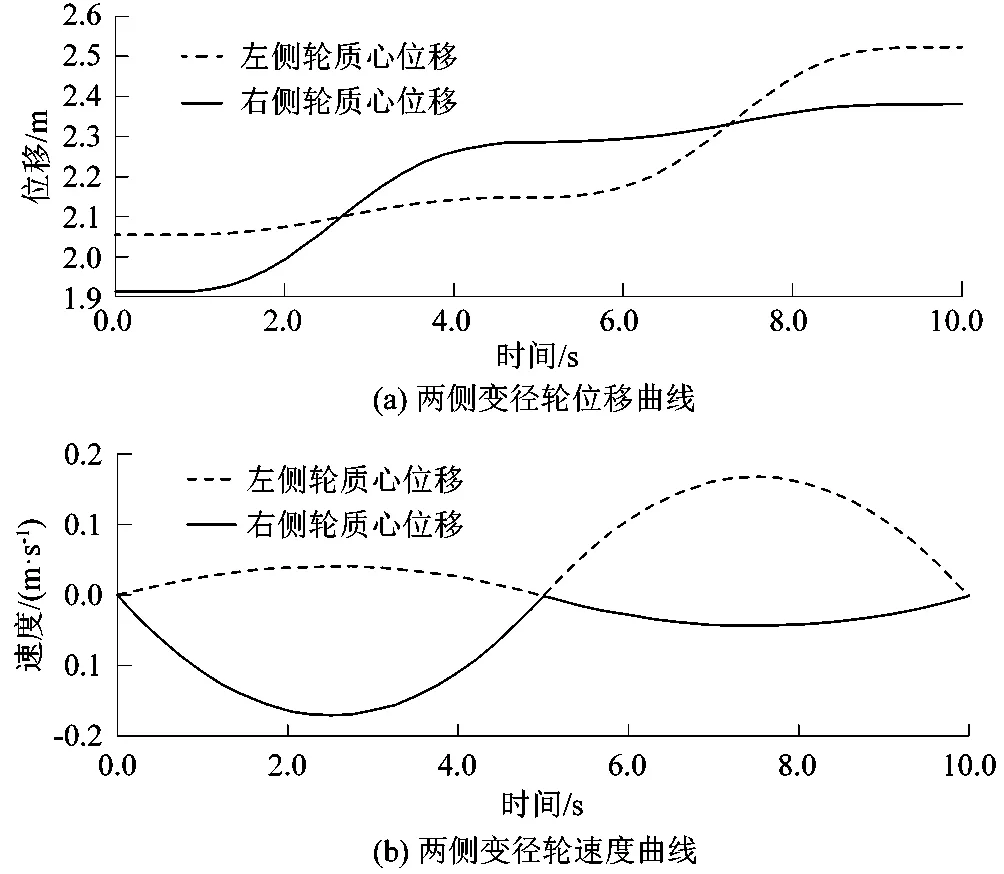
图5 “S”型转向运动过程中两侧变径轮的位移与速度曲线Figure 5 Displacement and speed curves of variable diameter wheels on both sides in process of "S" steering
4.3 机器人模式变换仿真
机器人模式变换过程仿真如图6所示。图6(a)所示为移动机器人轮式模式下的状态,即变径轮机构模式变换的初始状态,两侧的变径轮均为轮毂触地,为的是将整个移动机器人支撑在地面上。图6(b)所示为弧形腿开始接触地面,即为模式变换开始,此时移动机器人两侧的弧形腿支撑在地面。图6(c)所示为模式变换的最终形态,即机器人的轮腿式模式,弧形腿完全展开,越障性能大大提高。图6(d)所示为移动机器人从轮腿式模式又变换为轮式模式。

图6 轮腿可变式移动机器人模式变换示意图Figure 6 Schematic diagram of mode transformation of wheel-legged variable mobile robot
由图7可知在模式变换过程中,时间约为2 s时,其质心高度会随着弧形腿展开而上升;时间约为4.2 s 时,其质心高度达到最大值,即此时变径轮机构完全展开,机器人已处于轮腿式模式;从峰值至最终时刻,其质心高度逐渐下降,移动机器人从轮腿式模式恢复为轮式模式。移动机器人质心波动曲线光滑且没有突变点,波动最大幅值为73.5 mm。
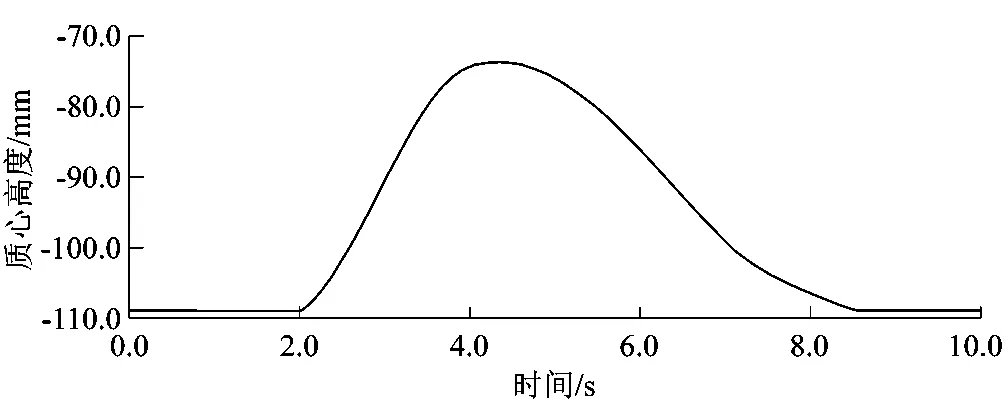
图7 模式变换过程中质心高度变化曲线Figure 7 Height change curve of centroid during mode transformation
5 结论
课题组设计了一种新型的轮腿可变式移动机器人,通过变径机构的设计,使得移动机器人能够完成轮式模式和轮腿式模式2种工作模式的切换。通过对模式变换原理的分析,证明了该机器人工作模式切换的可行性。建立了移动机器人轮式模式下的运动学和动力学模型,并通过ADAMS仿真软件,对移动机器人直行、“S”型转向以及模式变换过程进行仿真实验了分析,结果表明:移动机器人整机设计合理,具有结构紧凑,运动平稳,地形适应能力强的特点。本研究为后续移动机器人控制系统的设计提供了基础和参考。后续可针对机器人智能传感器以及全自动控制进行研究,以应用于灾难救援、情报侦察等各种复杂多变环境中。

