基于改进的稀疏最小二乘双子支撑向量回归的数字预失真技术
代志江 孔淑曼 李明玉* 蔡天赋 靳 一 徐常志
①(重庆大学微电子与通信工程学院 重庆 400044)
②(中国空间技术研究院西安分院 西安 710100)
1 引言
卫星通信逐步向高频段、大容量、高频谱效率的方向发展,对星载射频前端发射机非线性补偿系统的设计提出新的挑战[1]。一方面,多载波、多电平、高峰均比的高阶非恒包络信号的接入使得终端功率放大器(Power Amplifier, PA)工作于回退区,效率急剧下降,同时,功放非线性产生的交调失真落在带内带外,严重降低了信号质量和频谱效率[2];另一方面,星载射频前端功率放大器具有不连续的非线性失真特点,展现出动态发散及失真突变等现象,此外,传输带宽的增加将显著凸显射频PA的记忆效应,传统的数字预失真(Digital PreDistortion,DPD)模型很难取得良好的补偿效果[3]。因此,开发新型宽带高效低复杂度非线性失真补偿技术成为解决大容量卫星通信可靠传输问题的关键。
由于功放的强非线性和宽带信号的引入,传统多项式预失真模型,如记忆多项式、广义记忆多项式(Generalized Memory Polynomial, GMP),模型系数呈指数型增加,参数估计的精度对反馈噪声更加敏感,亟需采用剪切算法删减模型冗余项[4]。近几年,学术界提出使用压缩感知重构理论进行稀疏系统辨识,取得了不错的效果:Abdelhafiz教授团队[5]提出采用压缩采样匹配追踪算法进行内核选择,获得比主成分分析算法更好的剪枝性能和建模精度,但需要利用大量采样点进行筛选;之后,大量的研究在基于正交匹配追踪及其相应的改进算法上进行,这些算法常使用贪婪规则来稀疏化PA多项式模型[6–9]。尽管可以识别重要原子的位置,但是由于固定的批处理操作模式以及每次迭代时都涉及最小二乘法伪逆计算,在快速自适应方面的应用有所限制。同样,文献[10,11]针对双正交匹配追踪算法中的伪逆计算进行优化,分别采用递归操作和等效正交域变换方法避免求逆运算,提升算法求解速度,此外,研究者还将稀疏贝叶斯学习准则引入多项式核的修剪过程中,减少学习样本的同时还保持相当的线性化能力[12–14]。
以上的稀疏化方法均采用固定规则对多项式模型裁剪,在宽带强非线性失真情况下,过大的紧凑模型可能会存在稀疏辨识困难和模型删减不彻底等问题。最近的研究中,学者试图寻找脱离Volterra级数基础的模型来解决宽带系统的非线性辨识,人工神经网络以良好的非线性函数逼近能力被考虑进射频功放的行为建模及数字预失真器设计,而机器学习中支撑向量机(Support Vector Machines,SVM)模型有着精度与复杂度的良好折衷也被广泛用于数字补偿[15–19]。文献[18,19]针对支撑向量回归(Support Vector Regression, SVR)、双子支撑向量回归(Twin Support Vector Regression, TSVR)算法在PA非线性建模问题上进行了详细的描述,尽管模型表现出良好的泛化能力却仍存在一些问题:一方面,在处理大规模问题时,训练阶段的计算复杂度非常大,会出现训练失败情况;另一方面,大样本情况下,模型表现出的不稀疏性将严重增加预失真器设计时的复杂度。为优化以上问题,Cai等人[20]提出稀疏光滑的双子支撑向量回归(Smooth Twin Support Vector Regression, STSVR)模型用于发射机射频损伤的矫正,其主要思想是删减核矩阵和裁剪迭代计算中涉及的海塞矩阵,从而达到稀疏化模型和加速算法收敛速度的目的,但由于核矩阵的删减采用随机法,其建模精度可能会相应降低。
为解决大规模样本回归问题,本文将继续从支持向量机理论角度出发,采用最小二乘双子支撑向量回归(Least Squares Twin Support Vector Regression, LSTSVR)结构,同时考虑模型稀疏性以及快速自适应问题,提出了一种用于补偿星载发射机非线性失真的新型模型——改进的稀疏最小二乘双子支撑向量回归(Improved Sparse Least Squares Twin Support Vector Regression, ISLSTSVR)。为提高鲁棒性,该模型用截断的损失函数替代LSTSVR中的最小二乘损失函数以构建原空间的目标函数;为进一步提高运算速度,该模型采用Cholesky分解迭代寻找核矩阵中的基本核列来简化核矩阵从而得到相应的稀疏解。通过预失真实验表明,基于该逆模结构的预失真系统的补偿性能优于其他线性度较好的预失真系统。
2 基于改进的稀疏LSTSVR (ISLSTSVR)的PA建模方法
2.1 基于非凸截断最小二乘损失函数的LSTSVR
首先,将传统TSVR模型中带不等式约束的凸二次规划问题替换为等式约束优化问题,得到原空间LSTSVR的等价目标函数为
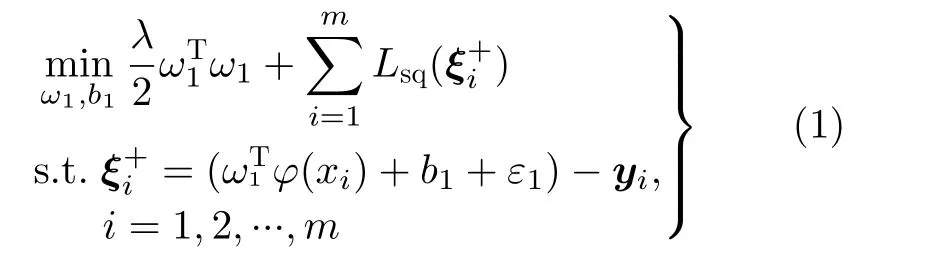

将式(8)代入优化目标式(6)和式(7)中,得到目标函数为
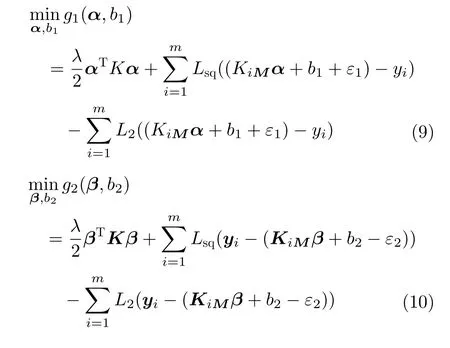
其中,α和β均为拉格朗日乘子,K为高维特征空间的核矩阵


2.2 基于改进的稀疏LSTSVR(ISLSTSVR)的PA建模方法
由于2.1节所构建的模型在求解过程中,核矩阵K∈ℜm×m要反复参与迭代运算,消耗了大量的存储和计算资源。注意到,半正定矩阵K通常不满秩,于是下面对K进行低秩近似和不完全分解。
假设输入样本的索引集为M={1,2,...,m},B是一个基本集B∈ℜr×r,用来存放挑选出的有用向量,且B∈M,N为非基本集,N=MB,用于存放样本集中有用向量之外的其他向量。依据Nystrom逼近原理[24],原来的核矩阵K可以用低秩矩阵K˜近似逼近,即


2.3 改进的稀疏LSTSVR(ISLSTSVR)算法流程
基于ISLSTSVR的PA建模算法流程如图1所示。本算法主要分为两个阶段:基本集B和 基本核列P的求解;偏差迭代算法求解模型系数。其中J为偏差迭代的最大次数。

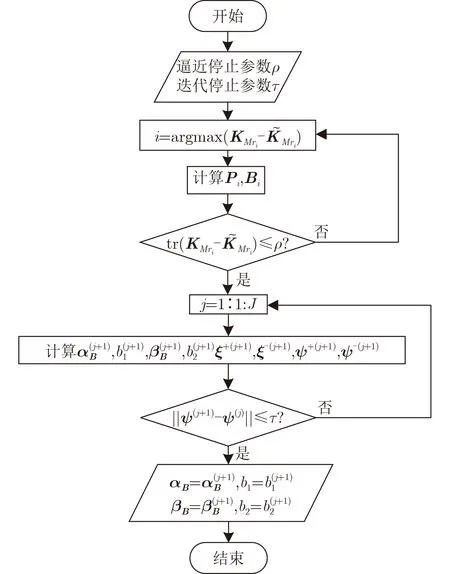
图1 ISLSTSVR算法流程图

3 基于ISLSTSVR的数字预失真系统
预失真的基本思想是预失真器和放大器的级联近似于线性或恒等运算符。基于ISLSTSVR的PA建模方法,本文采用间接学习结构,详细框图如图2所示。
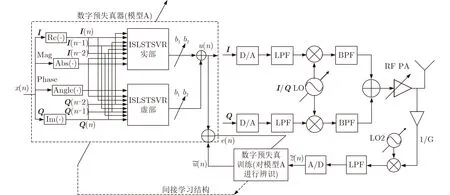
图2 预失真系统框图
先用PA的输入u(n)和 输出信号z˜(n)构建逆向模型,估计PA的后逆参数(α,b1),(β,b2),把后逆参数复制到预失真器中作为前逆补偿PA的非线性记忆特性。数据集的构建采用文献[18]中的时延结构,将时延的输入和输出信号分成实部和虚部。同时,为了增强对PA特性的描述,将输入信号的幅值和相位特性作为增强训练标签。基于此,输入和输出的完整关系可以写成:
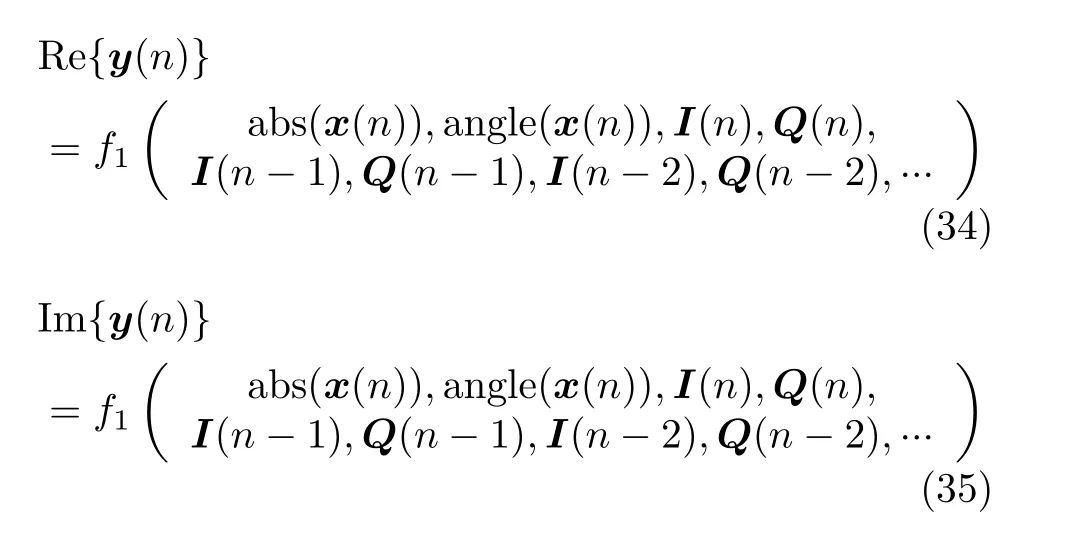
4 仿真实验及结果
为了进一步验证提出的基于ISLSTSVR模型的DPD方案的有效性。利用计算机(PC)、数字电源、功率放大器(PA)、Xilinx Zynq UltraScale+ RFSoC评估板(ZCU111)、矢量信号分析仪(Vector Signal Analyzers, VSA)、衰减器、耦合器、驱动放大器等搭建预失真验证平台,如图3所示。

图3 实验平台现场图
其中,预失真系统的前馈路径由RFSoC的片上DAC(基带信号发送)、驱动放大器、被测设备(PA)组成;反馈路径上的PA输出经衰减器和耦合器后功分两路,分别连接至频谱分析仪(反馈信号观测)以及RFSoC的片上ADC(采样PA输出);所有的数字信号处理部分均在MATLAB中进行。实验中,利用MATLAB串口模块下载符号速率为40 Msym/s的32QAM测试信号于RFSoC评估板中,在经Tx路径后激励待测功放(基于单管氮化镓(GaN)器件的宽带AB类PA(0.5-3 GHz),工作频点1.8 GHz,饱和输出功率45.5 dBm);一路功分信号被安捷伦公司的N9010A EXA信号分析仪采集进行实时频谱检测,另一路功分信号被RFSoC评估板ADC模块所采集,并通过串口传回MATLAB进行时间对齐处理。RFSoC评估板(ZCU111)使用300 MHz的参考时钟运行,可实现600 MHz基带采样率内信号的下载,内置DAC核采用8倍内插模式,可实现0-2.4 GHz的直接频率转换发射,ADC时钟配置2.4 GHz以实现宽带射频信号直采任务。测试步骤如下:
(1)采用ADS2018设计的32QAM信号,符号速率为40 Msym/s,滚降系数为0.22,8倍过采。下载40000个点到RFSoC评估板。
(2)以320 Msps的采样率采集功率放大器的输出信号用作后逆输入;
(3)基于ISLSTSVR建模方法,构建功放后逆模型,提取后逆参数;
(4)将后逆参数复制于前逆模型并与PA级联,采集预失真系统的输出信号测试线性化效果;
(5)对比TSVR, STSVR, ISLSTSVR 3种逆模预失真算法的线性化效果。
为了验证所提ISLSTSVR算法的建模效果,对实测的PA输入输出数据进行正向建模,并与GMP,SVR, TSVR, STSVR进行对比。首先,对于GMP模型,设置记忆深度M=4 ,非线性阶数P=9;对于幅度相位增强结构的4种SVR模型,设置记忆深度为M=2,采用高斯核函数映射。其次,对于采用光滑损失函数的STSVR和ISLSTSVR模型,设置平滑参数p=104。最后,将ρ=10−3设置为ISLSTSVR模型中Nystrom逼近的停止参数,并将τ=10−10设置为迭代的停止参数。为保证模型的泛化性能,从经过时间对齐和归一化后的样本集中选取无交集的训练集和测试集。

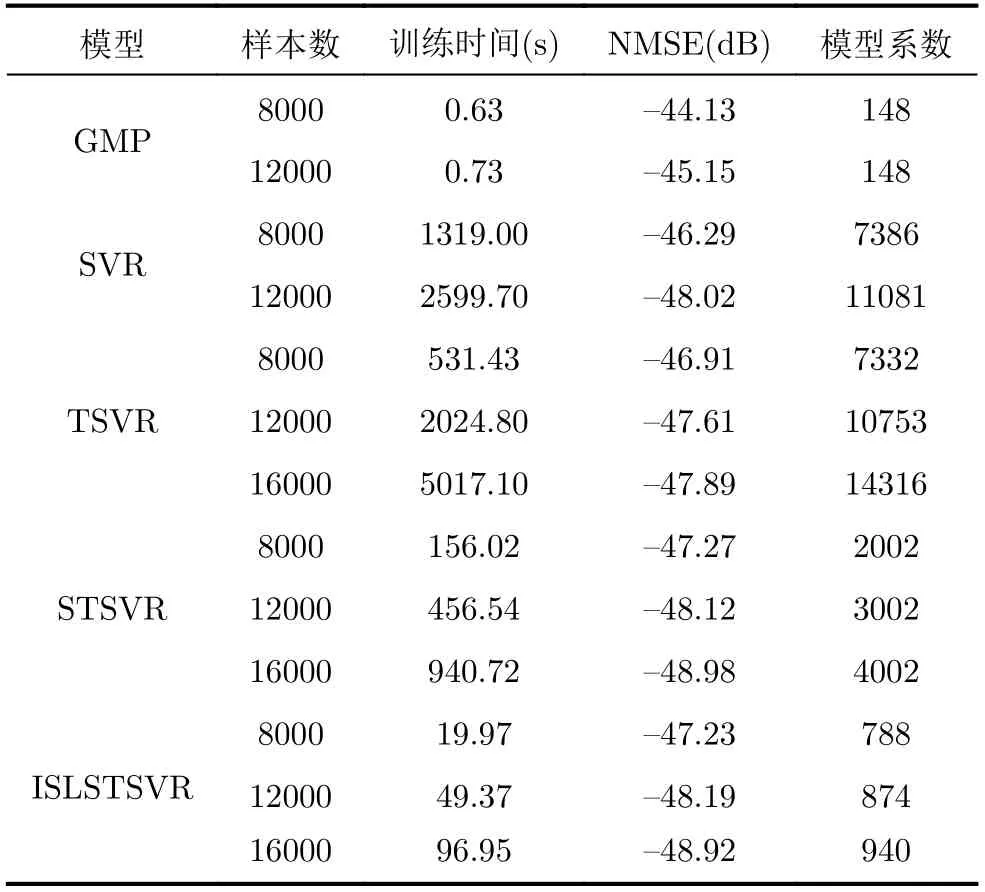
表1 不同样本集大小的机器学习模型建模效果对比

同样,通过数字预失真实验对功放的失真特性进行测量。本实验所用的AB类PA的AM/AM曲线与AM/PM曲线绘制分别如图4紫色和蓝色所示;基于ISLSTSVR的逆模预失真系统对PA的AM/AM, AM/PM失真的矫正效果分别如图4黄色和橘色直线所示。图4显示预失真系统的输出信号幅度随输入线性变化,且输入输出信号的相位差近似为0,表明PA的非线性在本文所提预失真结构下得到很好的矫正。
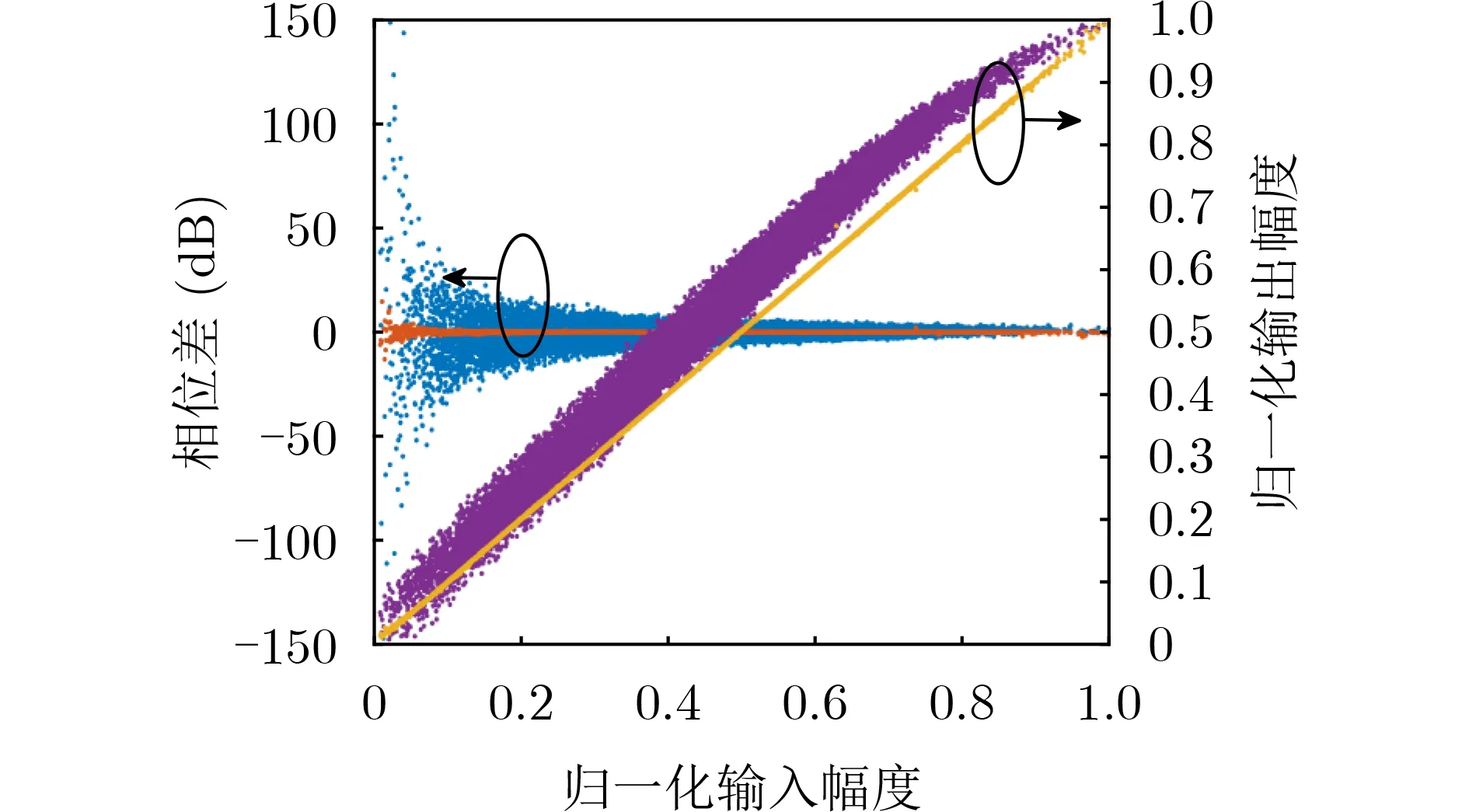
图4 ISLSTSVR逆模预失真的AM/AM, AM/PM曲线
对所提出的ISLSTSVR预失真系统的补偿性能进行测试,功率谱密度如图5所示。与其他模型相比,该模型的输出谱线性化效果最好,线性化后的PA输出信号,其邻信道功率接近系统底噪水平。此外,对相邻信道功率的抑制表明,该方法有效地抑制了带外频谱的扩展。为了定量分析补偿效果,表2给出了各模型补偿下的ACPR测量值。在–30 MHz下,该模型可以抑制约20.60 dB,在+30 MHz下,该模型可以抑制约19.77 dB。与线性化能力最强的STSVR模型相比,改进幅度为1.3 dB以上,表明所提出的DPD模型具有良好的补偿性能。
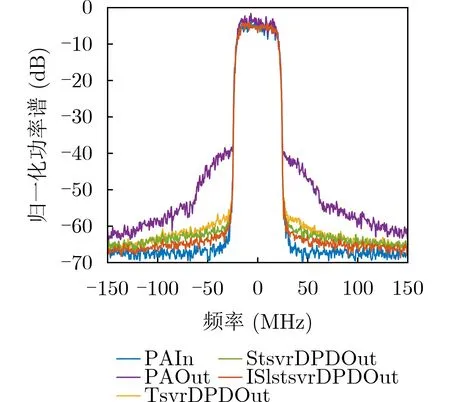
图5 不同模型预失真输出信号的功率谱密度对比
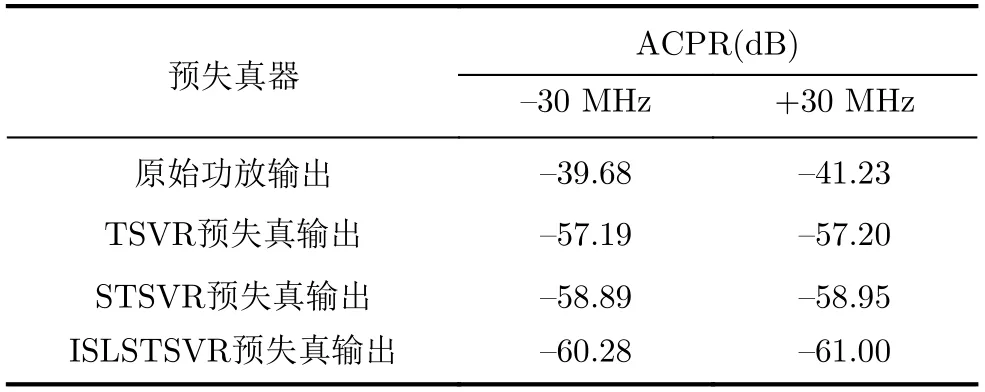
表2 不同模型预失真性能比较
5 结束语
本文提出了一种基于改进的稀疏最小二乘TSVR(ISLSTSVR)的低复杂度DPD方法,该方法首先使用改进的损失函数建立基于LSTSVR的功率放大器模型,随后围绕简化模型系数的目的,在求解过程中采用Nystrom逼近和Cholesky分解对核矩阵进行低秩近似从而降低运算复杂度。最后将该模型用作PA后逆估计,提取预失真参数。预失真实验表明该方法在保证精度的同时模型系数显著减少,使其能够成为未来卫星通信预失真系统的可行解决方案。

