基于多尺度多方向Gabor变换的Tsallis熵阈值分割方法

邹耀斌 张进玉 周 欢* 孙水发 夏 平

①(三峡大学大数据研究中心 宜昌 443002)

②(湖北省水电工程智能视觉监测重点实验室(三峡大学) 宜昌 443002)

③(三峡大学计算机与信息学院 宜昌 443002)

1 引言

图像分割是计算机视觉研究领域低层次视觉中重要的研究方向之一[1,2]。在已有的图像分割方法中，例如阈值分割、区域分割、聚类分割、深度学习分割，阈值分割因其简单和易于实现的优势而被广泛地应用到不同图像处理任务中[3]，其基本原则是将图像中每个像素的灰度值与选取的阈值进行大小比较，以此来决定该像素是属于目标还是背景，因而阈值分割的关键在于如何确定合适的阈值。

在众多阈值分割方法中，应用了信息论中熵概念的熵阈值法颇具代表性，它们大体可以分为两类：一类以最大化图像中背景熵和目标熵的和为原则来选择阈值，由该思想衍生而来的方法主要有最大香农熵法[4,5]、最大Rényi熵法[6–8]、最大Tsallis熵法[9–11]、最大Arimoto熵法[12,13]、最大Masi熵法[14]和最大Kaniadakis熵法[15]等。另一类则以图像分割前后信息量差异最小化为原则来选择阈值，其代表性的方法是最小熵阈值法[16]。在第1类方法中，除最大香农熵法，其他方法涉及的熵计算模型都有熵参数。分割不同直方图模态的灰度图像通常对应不同的熵参数，而自动选取合理熵参数的算法依旧缺乏，这在很大程度上限制了这些最大熵阈值方法的适应性。第2类方法将二值化问题转换为最小熵高斯拟合问题，它忽略了目标和背景之间的相互关系，难以分割非对称性直方图模态的灰度图像[16,17]。

不少熵阈值法结合离散概率分布和熵计算模型来计算相关的熵[4,6,9,12,14,15]，但它们都有一个共同的不足：没有考虑图像像素间的相关性，这使得同一个熵阈值法对于具有相同直方图的两幅不同图像将产生相同的阈值。此外，当一个灰度值的离散概率非常小的时候，容易引入大的计算误差从而降低获得阈值的鲁棒性。后续研究相继提出2维阈值法和3维阈值法。2维阈值法同时考虑图像灰度信息和邻域平均灰度信息，分割效果一般要优于1维阈值法[5,10,11,13]。3维阈值法在2维阈值法的基础上又加入了邻域的中值信息，这类算法对于具有混合噪声的图像有较好的分割效果[7,8]。2维或3维阈值法虽在一定程度上弥补了1维阈值法的不足，但其计算复杂度却远高于1维阈值法[8,11]。

现有熵阈值法除了上述不足外，还有一个关键问题是分割适应性较差。许多灰度图像因受噪声、点扩散或者背景和目标大小等因素影响，其灰度直方图呈现为无模态、单模态、双模态或者多模态，而现有熵阈值法一般较适合处理具有单模态长拖尾直方图的灰度图像，却难以兼顾其他情形。为了在统一的方法框架内从上述4种不同直方图模态的灰度图像中自动地选择出合理的分割阈值，提出了一种基于多尺度多方向Gabor变换的Tsallis熵阈值分割方法(Tsallis Entropy thresholding based on Multi-scale and multi-direction Gabor transform,MGTE)。MGTE方法将不同灰度直方图模态转换成统一的单模态，这种转换借助多尺度乘积效应来实现，其转换方式兼顾像素的灰度分布和像素间的空间位置。在获得4个方向上的单模态灰度直方图后，采用Tsallis熵作为熵计算模型来分别选取4个方向上的阈值，最后通过对4个方向上的阈值进行加权求和以作为最终分割阈值。

2 Gabor滤波器奇部及其多尺度乘积效应

2维Gabor滤波器由高斯信号和复正弦信号调制而成[18]，它可以表示为

注意到大小为( 8σ+1)×(8σ+1)的高斯核与图像进行卷积所得结果可以充分逼近完整高斯分布与图像进行卷积所得结果[19]，且在对数字图像卷积时，卷积核大小一般为奇数，由此可以推出σi=0.25×i(i ≥1)。Gabor滤波核中平行条带的方向角具有中心对称性，又因方向角等间距取值，即θr=rπ/m(r=0,1,...,m)，而式(5)又通过模运算计算图像kθ(σ)， 故θr取值可限制在[ 0,π/2]内。另外，方向太多容易造成图像方向性信息冗余并显著增加运算时间，而方向太少则可能遗漏重要方向性信息，经过反复试验最终确定使用4个方向角：0 ，π /7 ，2 π/7 和 3 π/7。

对2维Gabor滤波器的某一方向角度θr，定义图像f在该方向上的多尺度乘积图像为

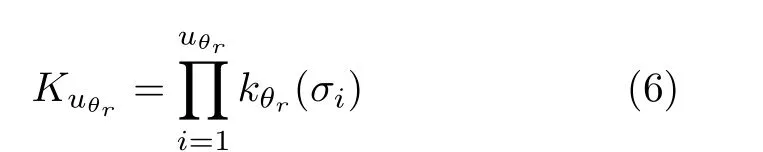
其中，uθr表 示在方向角度为θr时参与多尺度乘积变换的图像数量。多尺度乘积变换使得图像f的边缘信号和噪声呈现不同响应特点：当空间尺度增大时，噪声的响应值相对快速地减小，而边缘信号附近位置的响应值能相对保持良好。在图像Kuθr的灰度值被规范化到[0, 255]的前提下，随着uθr的增加，图像Kuθr的灰度直方图的众数逐渐趋于0，并且随着众数逐渐左移，灰度直方图中频数为0的灰度级逐渐增多，结果是[0, 255]的灰度分布越来越稀疏。Kuθr的灰度直方图与uθr之 间的关系表明：存在合适的uθr使得Kuθr中灰度级为0的频数足够大以抑制噪声，同时又保证频数为0的灰度级不能太多以维持边缘响应的多样性。为了自动计算这样的uθr值，第3节将引出Tsallis熵差的概念。

3 Tsallis熵差及其性质分析

定义S+−S为Tsallis熵差，下面4个命题揭示了Tsallis熵差的重要性质。值得注意的是，基于S+−S定义的Tsallis熵差不同于闫海霞等人[21]定义的局部Tsallis熵差。

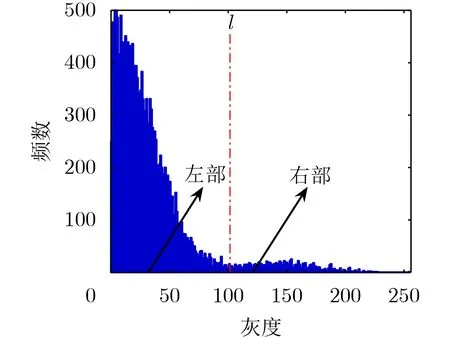
图1 灰度直方图的左右划分示意图

4 选取最终阈值的目标函数及算法步骤

5 实验结果与讨论

实验的主要软硬件参数如下：Intel Core i5-9300H 2.4 GHz CPU, 16 GB DDR2内存，Windows 10 64位操作系统，MATLAB 2018a 64位。测试图像包含合成图像4幅和真实世界图像40幅，它们以及对应的分割参考图像可以访问https://share.weiyun.com/UAmqSFkl获得。MGTE方法与交互式阈值(Interactive Thresholding, IT)方法[23]、迭代3类阈值(Iterative Triclass Thresholding, ITT)方法[24]、Tsallis熵阈值(Tsallis Entropy Thresholding,TET)方法[9]、快速鲁棒模糊C-均值聚类(Fast and Robust Fuzzy C-Means, FRFCM)方法[25]、迭代卷积活动轮廓分割(Iterative Convolution Active Contour, ICAC)方法[26]进行比较。其中，IT方法通过交互式选取分割阈值，该阈值对应的二值图像具有最小的误分类率(Misclassification Error,ME)。ME是一个常用的分割精度评估指标[3]，它表示在分割结果图像中误将背景作为目标及目标作为背景的百分比。IT方法可作为其他比较方法在分割精度方面的参考。

5.1 在合成图像上的比较实验

为了检验6个方法对4种不同直方图模态图像的分割适应性，将它们分别在4幅合成图像上进行分割实验(见图2)，它们的灰度直方图分别呈现为无模态、单模态、双模态和多模态(见图3)。图3、图4以及表1给出了6个方法在这4幅合成图像上的定性和定量比较结果。值得注意的是，图3中间绿色区域显示了对应的灰度直方图，4条垂直线及旁边的数字标示了4个阈值分割方法选择的阈值。表1中前面4个方法为阈值分割方法，后面2个方法为非阈值分割方法，因此后面2个方法的阈值用*代替。

图2 分割实验

第1组实验测试了无模态合成图像，结合图3(a)和图4(a)以及表1的第1列数据，可以观察到：(1)TET和ITT的总体分割结果最差，它们的ME值分别是24%和22.22%，远大于其他方法的ME值；(2)ICAC的分割结果虽优于TET和ITT，但也存在明显误分割，其ME值为19.58%；(3)FRFCM的分割结果要优于ITT,TET和ICAC，其ME值为1.17%，但它的分割结果不稳定；(4)MGTE的分割结果明显优于其他4个方法，其分割结果和IT完全一致，ME值为0%，达到理论上的最优分割；(5)IT,MGTE, ITT和TET所得阈值分别为201, 201, 133,126，MGTE方法与IT方法所得阈值一致，优于其他2个阈值方法所得阈值。这些量化指标值显示MGTE在分割无模态合成图像上的相对优势。

第2组实验测试了单模态合成图像，结合图3(b)和图4(b)以及表1的第2列数据，可以观察到：(1)TET, ITT和FRFCM的误分割都很严重，它们的ME值分别达到48.57%, 28.80%, 39.43%；(2)ICAC和MGTE的ME值分别为0.02%和0.01%；(3)IT, MGTE, ITT和TET所得阈值分别为214,212, 162, 151。其中，MGTE与IT所得阈值差距甚小，明显优于其他2个阈值方法所得阈值。这些量化指标值显示MGTE在分割单模态合成图像上的相对优势。

第3组实验测试了双模态合成图像，结合图3(c)和图4(c)以及表1的第3列数据，可以观察到：(1)TET的误分割比较严重，其ME值达到了21.70%，远大于其他方法的ME值；(2)FRFCM的分割结果虽优于TET，其ME值为0.17%，但它的分割结果不稳定性；(3)MGTE和ITT的分割结果与IT完全一致，ME值都为0.01%；(4)ICAC的分割结果略优于MGTE,ITT和IT，其ME值为0%；(5)IT, MGTE,ITT和TET所得阈值分别为129, 129, 128, 73，其中，MGTE方法与IT方法所得阈值再次保持一致。这些量化指标值显示MGTE方法在分割双模态合成图像上的相对优势。

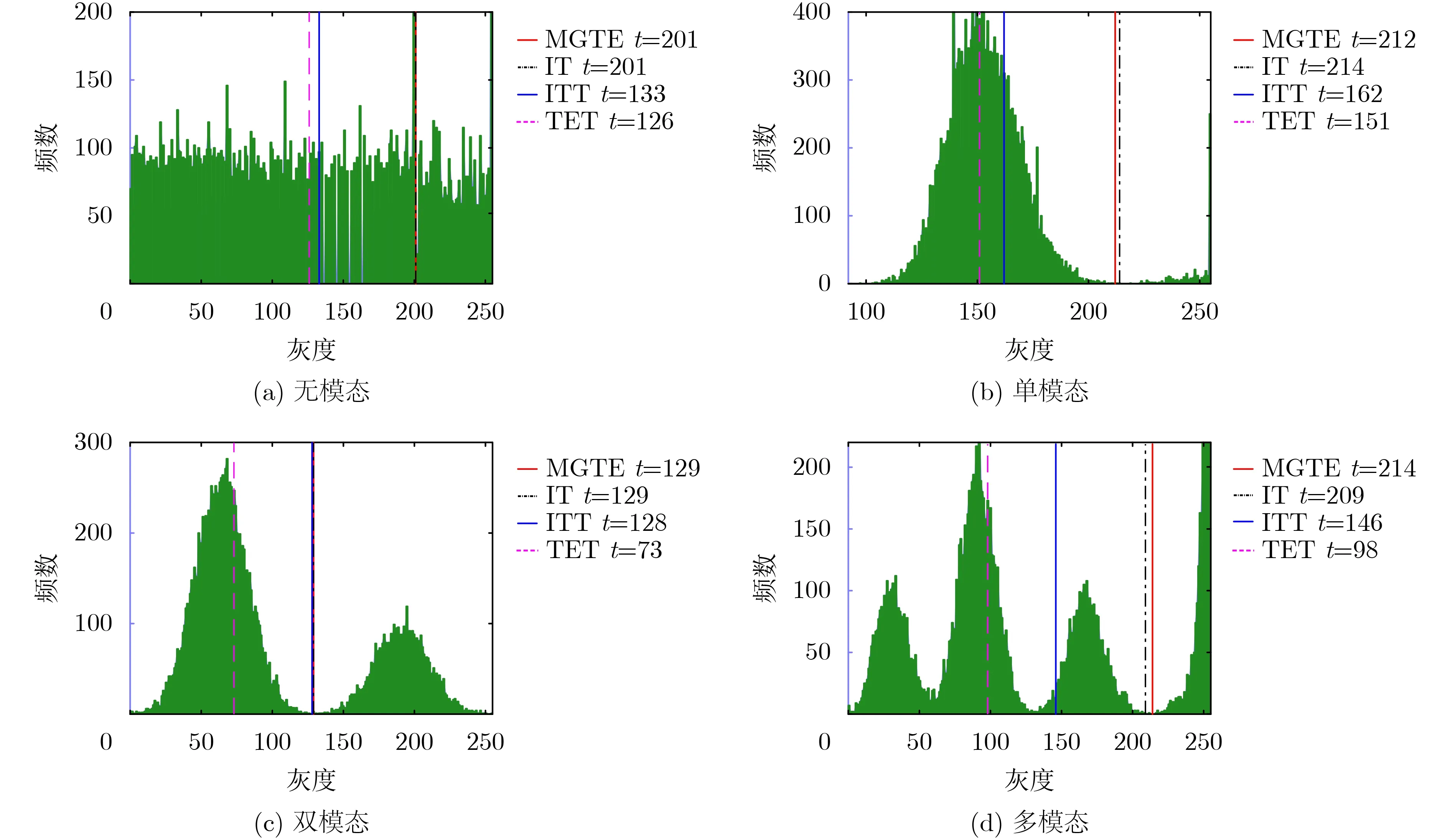
图3 4个模态合成图像的灰度直方图及不同方法所得阈值比较

第4组实验测试了多模态合成图像，结合图3(d)和图4(d)以及表1的第4列数据，可以观察到：(1)TET和ITT的误分割都较严重，它们的ME值分别达到28.16%和17.40%，远大于其它方法的ME值；(2)ICAC的分割结果优于TET和ITT，但在多模态合成图像上仍存在误分割，其ME值为2.95%；(3)FRFCM的分割结果虽优于TET, ITT和ICAC，其M E 值为0.8 7%，但它的分割结果不稳定；(4)MGTE与IT的分割结果差距甚小，它们的ME值分别为0.01%和0%；(5)IT, MGTE, ITT和TET所得阈值分别为209, 214, 146, 98。其中，MGTE与IT所得阈值差为5，明显优于其它2个阈值方法所得阈值。这些量化指标值显示MGTE在分割多模态合成图像上的相对优势。

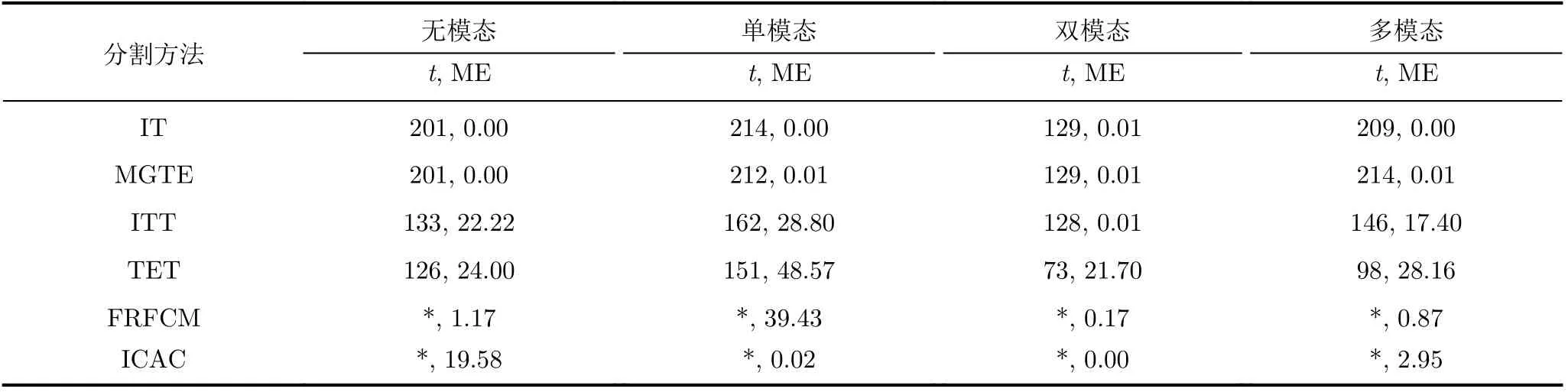
表1 6个分割方法在4幅合成图像上的分割阈值t 和ME值(%)

图4 不同分割方法在4个模态合成图像上的分割比较

5.2 在真实世界图像上的比较实验

为了进一步比较MGTE方法与其它5个方法的分割适应性，将6个方法分别在40幅真实世界图像上进行分割实验。这40幅测试图像中编号1～10,11～20, 21～30和31～40的图像分别对应无模态、单模态、双模态、多模态真实世界图像。

作为定性比较的代表性示例，图5(a)—图5(d)显示了编号为4, 17, 27和37的图像灰度直方图及4个阈值方法所得阈值，而图6展示了6个方法在这4幅图像上的分割结果。从图5(a)—图5(d)可以看到，MGTE所得阈值几乎非常接近IT所得阈值，而图6(a)—图6(d)也验证了MGTE能够相对成功地对这4幅测试图像进行目标和背景的分离。图7全面展示了6个方法在40幅真实世界图像上的ME量化结果，在每幅子图中，蓝色、红色、绿色和紫色的竖条分别标示了各分割方法在无模态、单模态、双模态和多模态情况下的ME值，而深蓝色水平虚线及其上的数字标示了对应情形下ME值的平均值。可以观察到：(1)对于无模态、单模态、双模态和多模态真实图像，MGTE的ME均值总体上更接近IT的ME均值，其对应的ME均值都小于0.9%；而其它方法，除ITT和FRFCM在双模态真实图像以及ICAC在单、双模态真实图像外，每种方法对应模态上的ME均值都大于14%；(2)ITT对于双模态真实图像有明显的分割效果，其ME均值为2.47%，但它对于无模态、单模态和多模态真实图像存在明显的误分割，其各自的ME均值都超过了19%；(3)TET对于无模态、单模态、双模态和多模态真实图像的误分割都很严重，各自的ME均值都超过28%；(4)FRFCM虽对双模态真实图像有明显的分割效果，其ME均值为4.71%，但FRFCM的分割结果不稳定，它在对同一幅图像进行多次聚类时，其ME值会存在很大差异；(5)ICAC虽适合单模态和双模态真实图像，其ME均值分别为5.25%和1.80%，但不适合无模态和多模态真实图像。这些都表明MGTE对无模态、单模态、双模态和多模态真实图像具有更强的分割适应性。

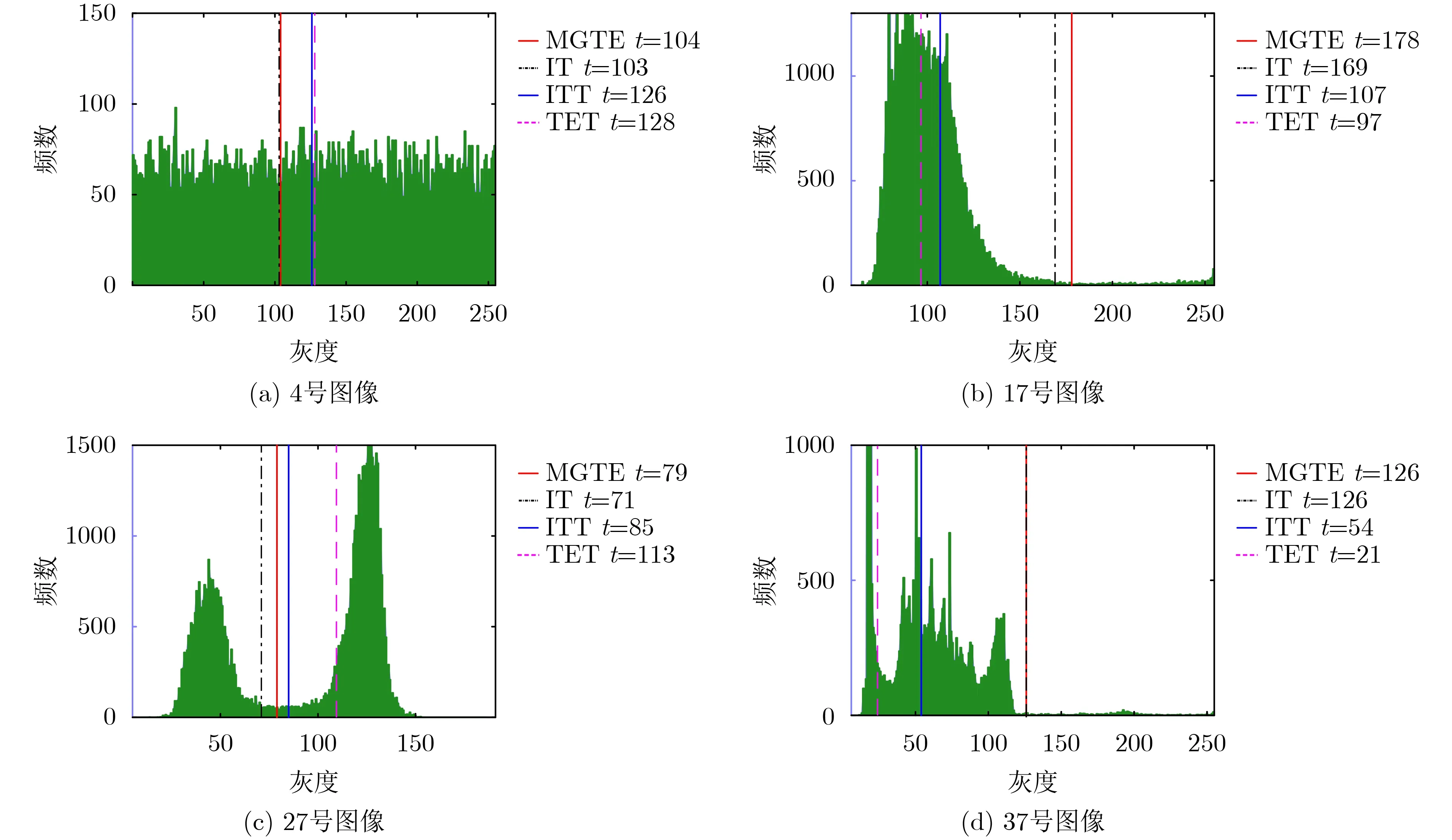
图5 4个不同编号真实世界图像的灰度直方图及不同方法所得阈值比较

图6 不同分割方法在4个编号真实世界图像上的分割结果比较

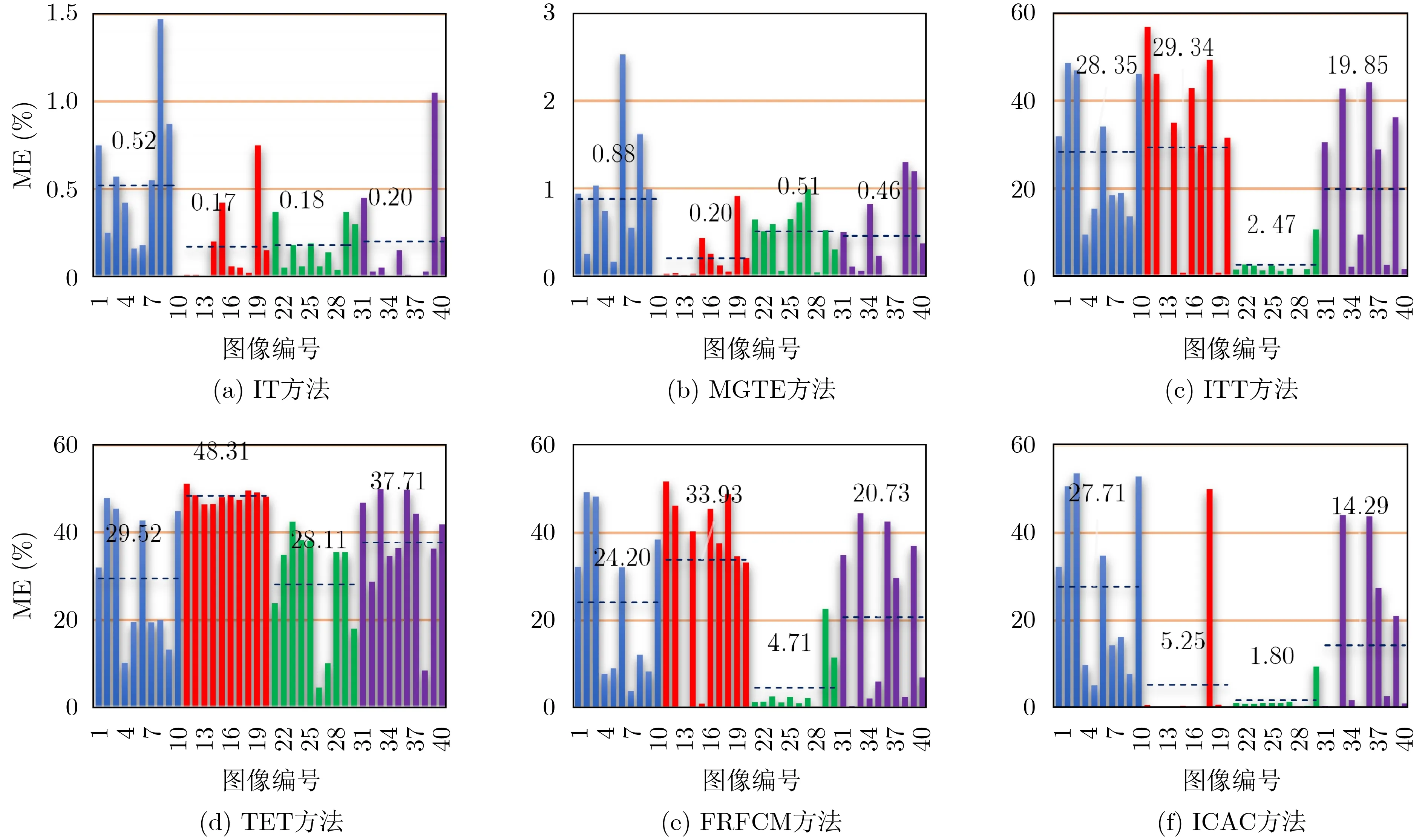
图7 6个分割方法在40幅测试图像上的ME值比较

5.3 计算效率比较

在相同软硬件参数下，同一个方法多次作用在同一幅图像上的CPU运行时间会在一定范围内波动。为了降低CPU运行时间波动的影响，每个方法将对同一幅图像分别进行10次测试，记录10次的CPU运行时间再求均值，以此均值作为该图像上的CPU耗时。依次可计算出5个自动分割方法在4幅合成图像和40幅真实世界图像上CPU耗时的均值和标准偏差。由表2可知：MGTE的CPU耗时最长，ITT, TET, FRFCM和ICAC的CPU耗时相对较短。

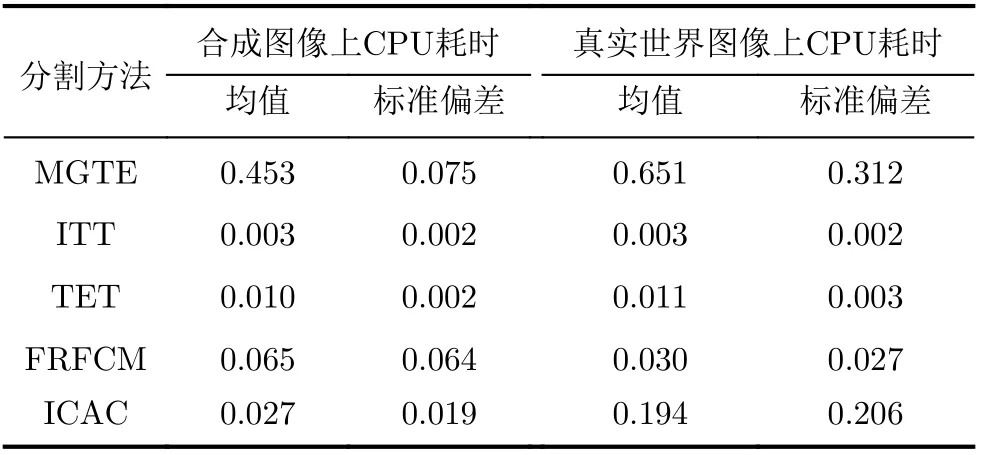
表2 5个分割方法的计算效率比较(s)

6 结束语

当灰度图像的灰度直方图呈现为无模态、单模态、双模态或者多模态时，相对于ITT, TET,FRFCM以及ICAC方法，MGTE方法的分割结果更加接近分割参考方法IT方法。MGTE方法的计算效率虽不及ITT, TET, FRFCM和ICAC方法，但它的分割精度更高，且在阈值选取方面具有更强的适应性。MGTE方法能够在分割精度、分割适应性上取得一定优势主要得益于：(1)MGTE方法的多尺度乘积效应能够将不同模态直方图转化成统一的单模态直方图；(2)在不同方向上，MGTE方法自动计算参与多尺度乘积变换的图像数量；(3)对不同方向上重构的灰度直方图进行Tsallis熵运算，所得阈值进行加权计算，这种加权策略使得选取的阈值更加接近合理阈值。