污水处理过程多变量自适应变论域模糊控制

周红标，李 杨，张庆宇，苏 衍，刘帅祥

(淮阴工学院自动化学院，江苏淮安 223003)

0 引言

活性污泥法是城市污水处理厂应用较为普遍的一种污水好氧生物处理方法[1-2]。在前置反硝化污水处理过程中，为了达到污水净化目的，主要有两个重要举措[3-4]。一是曝气池的鼓风曝气，主要通过活性污泥的有氧呼吸将有机物分解成无机物，其中曝气池溶解氧(dissolved oxygen，DO)浓度对微生物的生存环境有着重要的影响。若氧气不足，将会产生污泥膨胀，降低处理效果；若氧气过量，将会破坏微生物絮凝，降低悬浮固体沉降性，增加能耗成本。二是缺氧池的泵送内回流，其将好氧池的混合液回流到缺氧池中实现反硝化反应，其中缺氧池的硝态氮(nitrate nitrogen，NN)浓度决定脱氮除磷效果。若硝态氮浓度过低，将限制反硝化进程；若硝态氮浓度过高，将争夺过多的有机碳源，减弱厌氧放磷进程。因此，在污水处理过程中，对溶解氧和硝态氮浓度进行精确控制就显得尤为重要[5-6]。

针对DO和NN浓度控制问题，国内外学者进行了大量的研究。传统的控制方法多以开关控制、前馈控制和PID控制为主。文献[7]利用PI控制器控制DO浓度。文献[8]利用Ziegler-Nichols整定的PID控制器控制NN浓度。文献[9]构建一种多变量PID控制器，通过对控制参数进行适当整定，闭环控制性能得到极大提高。文献[10]设计一种鲁棒PID控制器用于DO浓度的跟踪控制，结果显示其在模型失配的情况下具有良好的鲁棒性。但是，由于污水处理过程的非线性、时变性和滞后性等特点，PID参数整定较为困难，控制精度不能满足实际需求。由于模型预测控制(model predictive control，MPC)具有在线预测、滚动优化和反馈校正的优点，有研究者将其应用于污水处理过程。文献[11]利用线性状态空间模型建立污水处理过程多变量MPC控制器。文献[12]利用简单动态矩阵控制建立污水厂多变量MPC控制器。文献[13]在污水处理过程三阶简化模型基础上构建MPC控制器，并进行DO浓度恒定和阶跃变化两种工况下的实验验证，结果表明MPC的控制精度优于PID控制。但是，由于污水处理过程的上述特点，MPC所需的精确数学模型难以建立，控制效果得不到保证。

模糊逻辑控制(fuzzy logic control，FLC)利用领域专家知识设计模糊规则库，不需要被控对象的精确数学模型，具有通用逼近性以及对输入输出映射关系的可解释性，在污水处理过程底层回路控制中得到广泛应用。文献[14]利用FLC对序批式污水处理过程DO浓度进行恒定值控制，结果显示FLC的控制精度优于PID控制。文献[15]利用Lyapunov综合分析法设计模糊规则后件参数的自适应调整策略，构建了DO稳定控制的自适应模糊控制器(adaptive fuzzy control，AFC)，结果表明AFC无需数学模型，取得了较高的控制精度。文献[16]和文献[17]也相继提出了改进型的AFC方法。文献[18]提出一种监督启发式模糊控制器设计方法，解决间歇反应器的溶解氧控制问题。但是，FLC和AFC都属于静态模糊系统，在控制过程中隶属函数的结构和参数都保持不变，系统的插值精度、稳定性和鲁棒性并不能得到很好的保证。

变论域模糊控制(variable universe fuzzy control，VUFC)通过论域伸缩因子的收缩相对地增加误差零点附近的控制规则个数，从而提高控制精度[19]，在锂电池充放电控制[20]、舰载机着舰控制[21]、电池均衡控制[22]、车辆稳定控制[23]等领域得到广泛应用。文献[24]采用VUFC对铝电解过程的AIF3添加量实施控制，从而提高了电解池的电流效率和稳定性。文献[25]采用VUFC对变速器的速比进行控制，从而提高了燃油经济性和动力性。文献[26]采用VUFC对风力发电机转速进行控制，并利用多种群遗传算法优化控制参数，从而降低了响应时间和超调量。文献[27]提出了一种隐变论域模糊控制(hidden variable universe fuzzy control，HVUFC)策略，采用无迹卡尔曼滤波算法估计隐藏变量，实现了对运动障碍的实时控制。但是，这些VUFC策略基本采用领域专家的主观经验设计模糊规则库，控制函数在传递到“后代”的进程中，会发生变形“失真”现象，严重影响控制器的性能[28]。

针对上述问题，本文提出一种自适应变论域模糊控制(adaptive variable universe fuzzy control，AVUFC)策略。在AVUFC中，根据性能指标设计了基于自适应差分进化算法的伸缩因子调整策略，能在每个采样周期内对伸缩因子进行寻优，从而在线调节隶属度函数的参数，增加了参数调整的自由度，缓解了变论域模糊控制的失真问题。最后，利用AVUFC解决污水处理过程DO和NN多变量精确跟踪控制问题。

1 污水处理过程

活性污泥法污水处理过程的工艺主要是由一级、二级、三级3个处理部分组成，其中二级处理是主体，通常是由生化反应池、二沉池、污泥回流系统和剩余污泥排放系统组成。为了便于进行算法研究、性能对比和工程验证，国际水质协会推出了活性污泥1号基准仿真模型(BSM1)。在BSM1中，生化反应池由2个厌氧池和3个需氧池组成，分别承担硝化和反硝化任务，具体工程布局如图1所示。

从图1可以看出，BSM1底层主要有2个控制回路：一是通过调节氧传递系数KLa5来控制第5单元的DO浓度SO,5；另一个是通过调节内回流量Qa来控制第二单元的NN浓度SNO,2。在BSM1中，DO和NN浓度均设置为固定值，分别为2 mg/L和1 mg/L，默认采用PID控制策略。然而，由于污水处理过程的生化反应机理复杂，表现出强非线性、强耦合、大时滞和不确定性严重等特性，控制参数的整定存在困难，PID控制性能难以满足实际生产需求。因此，本文采用自适应变论域模糊控制(AVUFC)来解决DO和NN的精确跟踪控制问题。

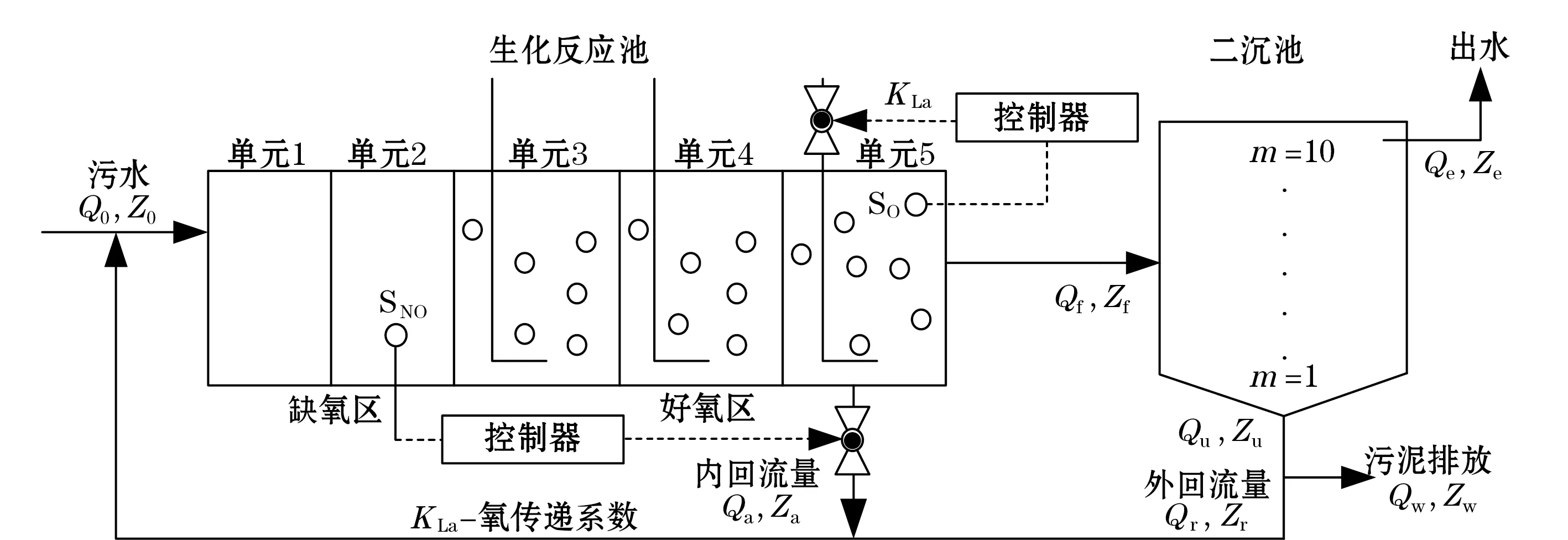
图1 BSM1的具体工程布局

2 变论域模糊控制原理

2.1 模糊控制原理

定义：设A={Ai}(1≤i≤n)是论域集X的一组模糊集，且满足：

(1)

假设Ai和Aj的峰值点分别为xi和xj(1≤j≤n)，当i≠j时，xi≠xj，则称Ai为A的一个模糊划分。

给定模糊控制器，Xi=[-Ei,Ei]是输入变量xi(i=1,2,…,n)的论域，而Z=[-U,U]是输出变量z的论域。Aj={Aij}(i=1,2,…,n，j=1,2,…,m)是论域Xi上的模糊划分，而C={Cj}是论域Z上的一个模糊划分。若A和C是语言变量，可形成如下的模糊控制规则：

Ifx1isA1j，andx2isA2j，and…，andxnisAnj，

ThenzisCj(j=1,2,…,m).

设xij为Aij的峰点，zj为Cj的峰点(i=1,2,…,n，j=1,2,…,m)，则基于上述模糊规则的模糊控制器输出z可以用如下的n元分段插值函数表示[19]：

(2)

特别地，针对一个双输入单输出模糊控制器(即输入x、y，输出z)，若A和B分别为2个输入论域的模糊划分，则该控制器输出可以表示成1个二元插值函数形式：

(3)

2.2 变论域模糊控制原理

变论域是李洪兴教授于1999年提出，其在模糊控制中引入伸缩因子动态调整论域的大小，能够在不改变模糊规则数的情况下，使得论域随着误差的缩小而收缩，从而取得响应速度和稳态精度的最佳平衡[19]。变化后的论域可表示为：

Xi(xi)=[-αi(xi)Ei,αi(xi)Ei]

(4)

Z(z)=[-β(z)U,β(z)U]

(5)

式中：[-Ei,Ei]和[-U,U]分别为输入变量xi和输出变量z的论域；αi(xi)与β(z)分别为论域Xi和Z的伸缩因子；相较于可变论域，Xi和Z为初始论域。

论域变化的情况如图2所示。可见在不增加模糊规则数量的前提下，随着论域收缩，模糊划分的峰点距离逐渐减小，从而提高控制器精度。

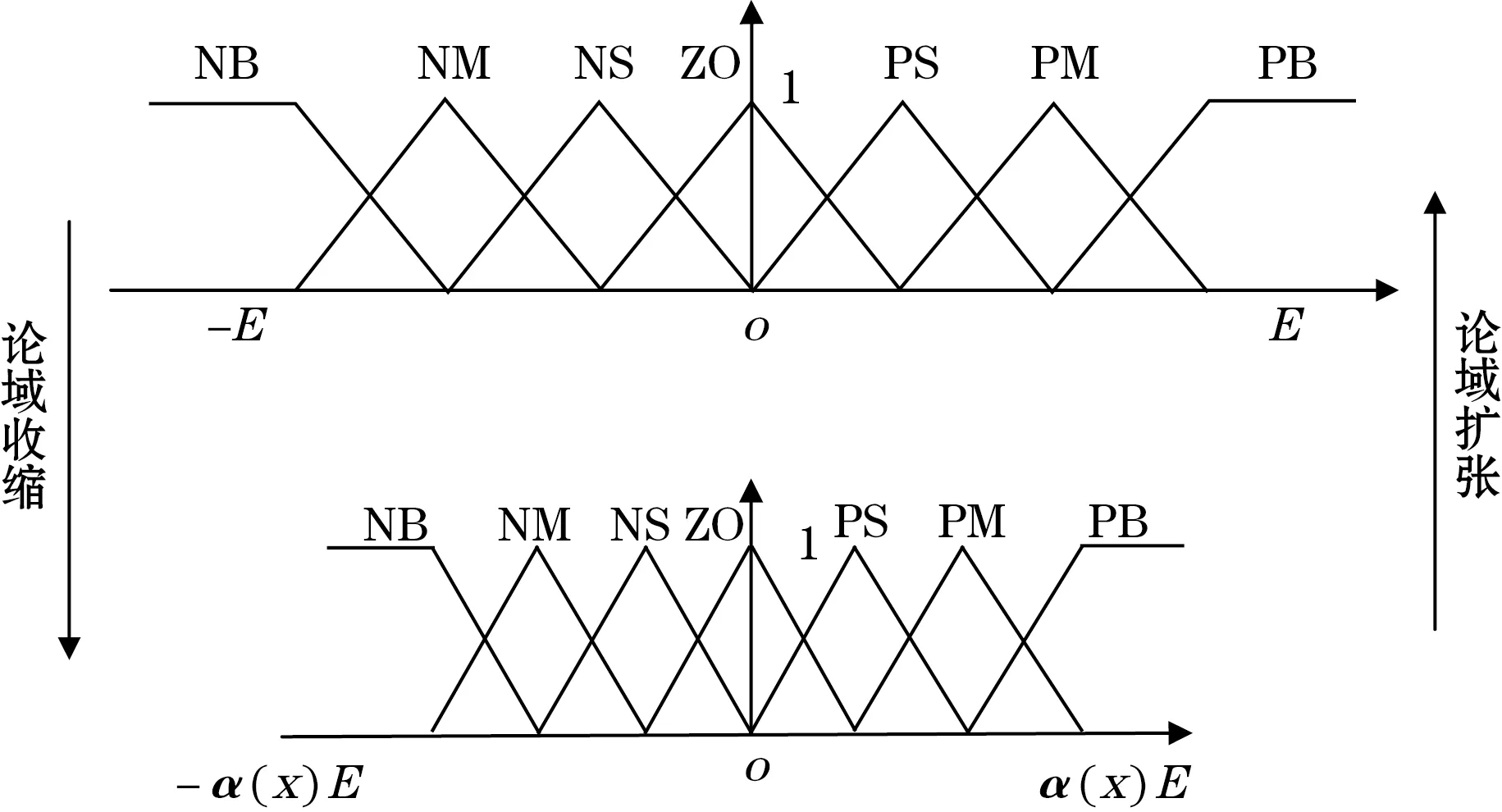
图2 论域的演化

李洪兴教授推荐2种变论域模糊伸缩因子，具体公式如下[19]：

(6)

(7)

式中：xi为第i个输入变量；ε为一个非常小的常数；λ为一个接近于1的常数。

根据式(6)，k越大，α(xi)越大，并且α(xi)的变化越剧烈；λ越大，α(xi)越小，但是α(xi)的变化越剧烈。因此，选取较小的k值和较大的λ值，不仅能够压缩论域的范围，而且能够提高系统的响应速度。

输出论域的伸缩因子通常选取为

(8)

式中：xi(τ)为输入变量xi在τ时刻的值；n为输入变量个数；θi和Pi为可调参数。

β(0)可根据实际情况调整，一般设定β(0)=1.0。其他较为简单的输出论域的伸缩因子的形式有

(9)

式中：E、EC和U分别为输入变量x、y和输出变量z的论域；τ1、τ2和τ3均在(0,1)之间。

因此，基于前述模糊规则的变论域自适应模糊控制可表示成如下的n元分段动态插值函数[19]：

(10)

式中x(t)=xi(t)(i=1,2,…,n)。

令θ(t)=[z1(t),z2(t),…,zm(t)]T为模糊规则后件参数向量，ζ(α,x,t)=[ζ1(α,x,t),ζ2(α,x,t),…,ζm(α,x,t)]T为模糊规则基函数，则式(10)可以简写成：

z[x(t+1)]=β(t)θT(t)ζ(α,x,t)

(11)

变论域通常有3种等价方法：

(1)直接对输入输出论域进行伸缩处理，即对论域各点乘以对应的伸缩因子；

(2)将输入论域初始值除以输入伸缩因子，输出量乘以输出伸缩因子；

(3)将模糊控制器的量化因子除以对应的伸缩因子，输出比例因子乘以对应的伸缩因子。

方法3相对简单，易实现。本文采用方法3设计自适应变论域控制器，能够以较小的计算量取得同样的变论域控制效果。

3 自适应变论域模糊控制

对式(11)作进一步分析发现，在模糊规则确定好的情况下，VUFC的控制性能主要取决于所设定的输入输出伸缩因子。然而，伸缩因子的数学结构与携带的参数主要凭经验设定，缺乏统一的标准，调节压力过大，使得控制品质难以得到保证。本文选取系统性能指标作为适应度函数，采用自适应差分进化算法对输入输出变量x、y、z的论域E、EC、U对应的伸缩因子αe、αΔe、βΔu进行寻优，获取每个采样周期的最佳伸缩因子，并将这些伸缩因子应用到AVUFC的下一个采样时刻。基于自适应差分进化算法的变论域模糊控制器结构图如图3所示。

图3 自适应变论域模糊控制器结构图

3.1 自适应差分进化算法

DE算法是一种模拟自然界生物群体进化的启发式搜索算法，主要过程包括初始化、变异、交叉和选择4个操作，简述如下[29]：

(1)初始化。在解空间中随机均匀产生N个个体，每个个体由D维向量组成，作为第0代种群，表示如下：

(12)

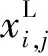
(13)

式中rand(0,1)表示区间[0,1]上的随机数。

(2)变异。DE算法利用差分策略进行个体变异，克服种群易陷入局部最优的缺陷。在第g次迭代过程中，对个体Xi(g)，从种群中随机选择3个个体Xr1(g)、Xr2(g)、Xr3(g)，且r1≠r2≠r3≠i，生成变异向量Hi(g)，即：

Hi(g)=Xr1(g)+F·[Xr2(g)-Xr3(g)]

(14)

式中F为缩放因子，一般在[0,2]之间取值。

(3)交叉。DE算法利用交叉操作依据一定的交叉概率生成新的试验向量Vi(g)，进一步为种群进化提供动力，表示如下：

(15)

式中：vi,j(g)、hi,j(g)、xi,j(g)分别为第g代时试验向量Vi(g)、变异向量Hi(g)和种群个体Xi(g)的第j维；Cr为交叉概率，Cr∈[0,1]。

(4)选择。DE算法利用贪婪选择策略选择较优个体作为新的个体，表示如下：

(16)

式中Xi(g+1)为第g+1代时种群中第i个个体。

可见，如果试验向量Vi(g)的适应度值小于种群个体Xi(g)，则下一代新个体Xi(g+1)取自于试验向量Vi(g)；否则，Xi(g+1)取自于Xi(g)。

考虑到差分策略、缩放因子F、交叉概率Cr对DE算法性能的影响较大，本文提出基于协同自适应策略的差分进化算法(ADE)。原始DE中变异操作采用rand/1/bin，此外还有rand/2/bin、rand/1/bin～等策略。rand/2/bin表示如下：

Hi(g)=Xr1(g)+F·[Xr2(g)-Xr3(g)]+

F·[Xr4(g)-Xr5(g)]

(17)

式中：r1、r2、r3、r4、r5是从[1，N]中随机选取的5个不同的整数。rand/1/bin～表示如下：

Hi(g)=Xi(g)+F·[Xr1(g)-Xr2(g)]

(18)

可见，rand/2/bin具有较强的全局探索能力，rand/1/bin～具有较优的局部搜索能力[30]。因此，在进化初期使用rand/2/bin，在进化中期使用rand/1/bin，在进化末期使用rand/1/bin～，表示如下：

(19)

式中Gmax为最大迭代次数。

此外，较大的F和Cr值能够使得种群继承更多的变异基因，从而提高种群的多样性；较小的F和Cr值有利于种群快速收敛。因此，在式(19)表示的进化过程的3个阶段，F和Cr都随迭代次数呈现非线性下降趋势，表述如下：

(20)

式中：Fmin、Fmax、γF分别设置为0.1、1.9、0.5。

(21)

式中：Crmin、Crmax和γCr分别设置为0.1、0.9、0.6。

综上，ADE的算法流程如下：

步骤1：参数初始化，包括N、Gmax、D、g等；

步骤2：利用式(12)和式(13)随机产生初始种群；

步骤3：根据适应度函数，对初始种群进行评价；

步骤4：利用式(19)对种群执行变异操作；

步骤5：利用式(15)对种群执行交叉操作；

步骤6：利用适应度函数对临时生成的种群进行评价；

步骤7：利用式(16)对种群执行选择操作，生成下一代种群；

步骤8：若g>Gmax，则停止；否则，g值加1，转入步骤4。

3.2 自适应变论域模糊控制流程

根据污水处理过程多变量控制需求，结合变论域模糊控制原理和自适应差分进化策略，给出如下的基于AVUFC的DO和NN多变量控制流程。

步骤1：参数初始化，主要为AVUFC的模糊分割数、量化因子等；

步骤2：在当前控制周期，根据当前被控量输出，获取DO和NN的误差e和误差变化量Δe；

步骤3：以e和Δe的平方和作为适应度函数，利用ADE算法对伸缩因子αe、αΔe和βΔu进行寻优；

步骤4：将ADE算法获取的最优αe、αΔe和βΔu应用到AVUFC的下一个控制周期；

步骤5：若控制结束，则停止；否则，转到步骤2。

4 实验验证

4.1 实验数据

BSM1基准模型自带14天的真实运行数据，包括晴好天气、阴雨天气和暴雨天气3种不同的工况，采样周期为15 min。3种工况下的入水流量Q0及入水有机物SS、氨氮SNH、固体悬浮物TSS的浓度如图4所示。可以看出污水处理过程受周中、周末、节假日和天气等因素影响，具有大时变、大时滞和强耦合等非线性特点。可以看出，在阴雨天气的第8～11天，可以明显观察到一个强降雨过程。

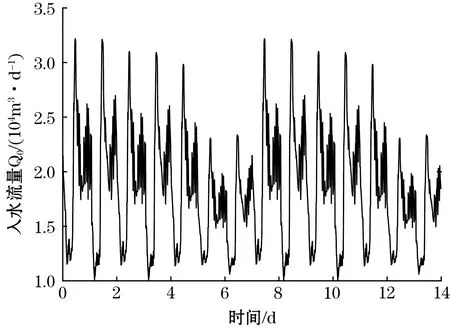
(a)晴好天气入水流量

4.2 性能指标

为了比较不同控制器的性能，BSM1模型中定义了IAE(绝对误差积分)、ISE(平方误差积分)和Devmax(距设定值的最大偏差)3个指标，具体公式如下：

(22)

(23)

Devmax=max{|e|}

(24)

式中e为设定值与真实值之间的误差。

IAE、ISE和Devmax分别体现瞬态响应、平稳性和抗干扰能力。

4.3 参数设置

本文所有控制器的采样周期Δt均设为0.75 min。针对SO,5和SNO,2的控制问题，分别设计了2个双输入单输出AVUFC控制器。溶解氧AVUFC的输入为设定值与溶解氧浓度之间的偏差eDO和偏差变化率ΔeDO，输出为生化池第5单元的曝气量kLa5。硝态氮AVUFC的输入为设定值与硝态氮浓度之间的偏差eNN和偏差变化率ΔeNN，输出为内回流量Qa。本文设置偏差的论域为[-6,6]，偏差变化率的论域为[-4,4]。为了实现控制量的精确跟踪控制，将输入输出量模糊化后定义为7个模糊子集，表示为

{NB,NM,NS,ZR,PS,PM,PB}

(25)

式中：NB、NM、NS、ZR、PS、PM、PB分别表示为负大、负中、负小、零、正小、正中、正大。

将输入输出变量的模糊论域E、EC和U都设置为13个等级，即：

{-6,-5,-4,-3，-2，-1，0，+1，+2，+3，+4，+5，+6}

(26)

本文选用高斯函数作为隶属度函数，并令离原点近的函数曲线较陡，离原点远的函数曲线较缓，这有利于提高跟踪速度和跟踪精度。E、EC和U的隶属度函数曲线相同，E的隶属度函数曲线如图5所示。

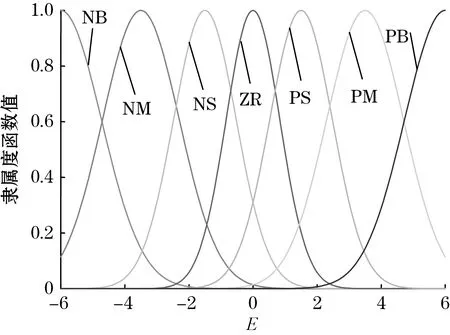
图5 E的模糊隶属度函数曲线

根据专家控制经验设计表1所示模糊规则表。

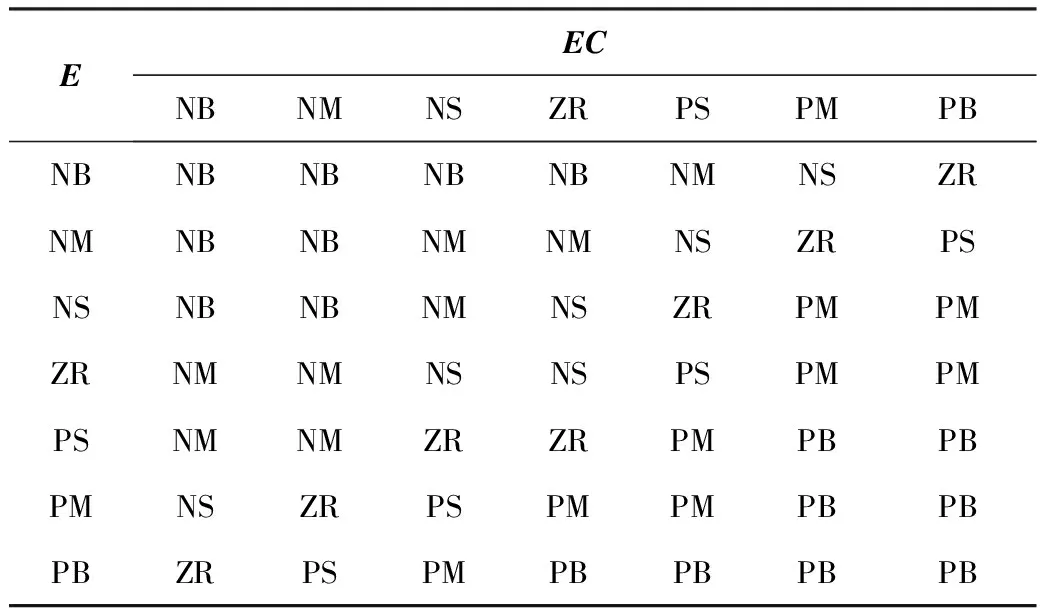
表1 模糊控制规则表

因此，基于自适应差分进化算法的变论域模糊控制器的实时输出为

(27)

式中：AVUFC为本文所设计的自适应变论域模糊控制器；Ke、KΔe和KΔu分别为误差e、误差变化量Δe和操作量变化量Δu的量化因子；αe、αΔe和βΔu分别为自适应差分进化算法优化出的伸缩因子。

为了评价AVUFC控制策略的有效性和先进性，选用PID、FLC、VUFC作为对比算法。对于PID控制器，DO和NN浓度控制器的比例、积分和微分系数分别设为200、15、2和50 000、5 000、400；对于FLC控制器，输入空间模糊分割数设为7，DO和NN浓度控制器的Ke、KΔe和KΔu分别为24、16、10和24、80、5 000。对于VUFC，伸缩因子采用指数型伸缩因子，具体为：

αe=1-0.6exp(-0.3e2)

(28)

αΔe=1-0.2exp(-0.5Δe2)

(29)

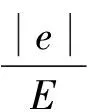
(30)

式中：e和Δe分别为误差和误差变化量；E和EC分别为输入变量e和Δe的初始论域；αe、αΔe和βΔu分别为输入输出伸缩因子。

4.4 结果与分析

下面分别对DO、NN的恒定值控制和变设定值控制进行实验验证，并与其他控制方法进行结果对比分析。

4.4.1 恒定值控制

按照BSM1基准要求，分别设置DO和NN的设定值为2 mg/L、1 mg/L，利用AVUFC控制器跟踪设定值。图6给出了晴好天气下PID、FLC、AVUFC的控制效果，图7给出了3种控制器的跟踪误差。为了清晰展示控制效果和控制误差，这里只给出了第8～10天的控制结果图。

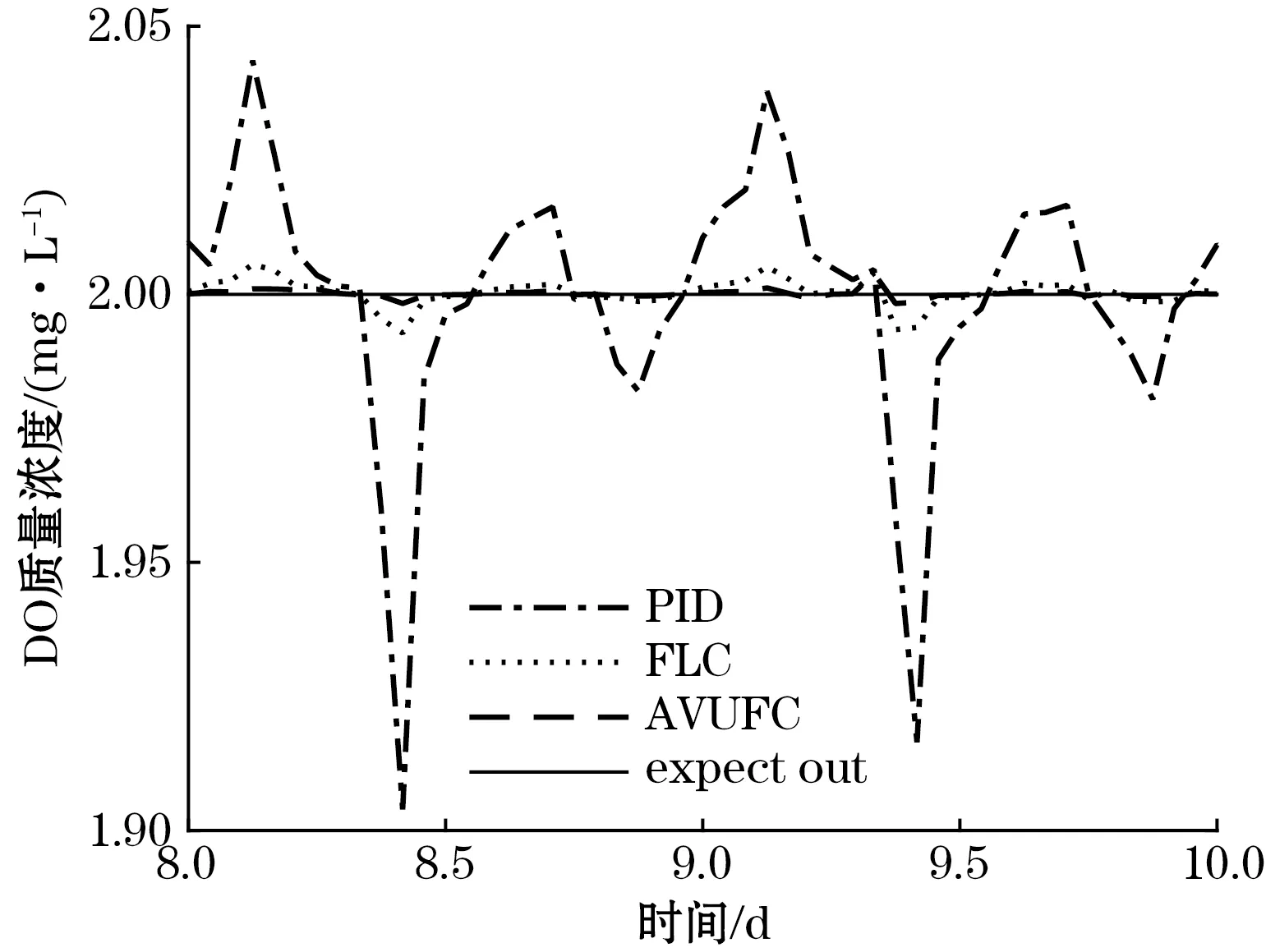
(a)DO的控制效果

从图6可以看出，AVUFC的控制效果要明显优于PID和FLC，表明本文所提控制策略的稳定性好、抗干扰性强。从图7可以看出，AVUFC的控制误差主要位于[-0.003,0.003]范围，明显小于PID和FLC，具有较高的跟踪控制精度。

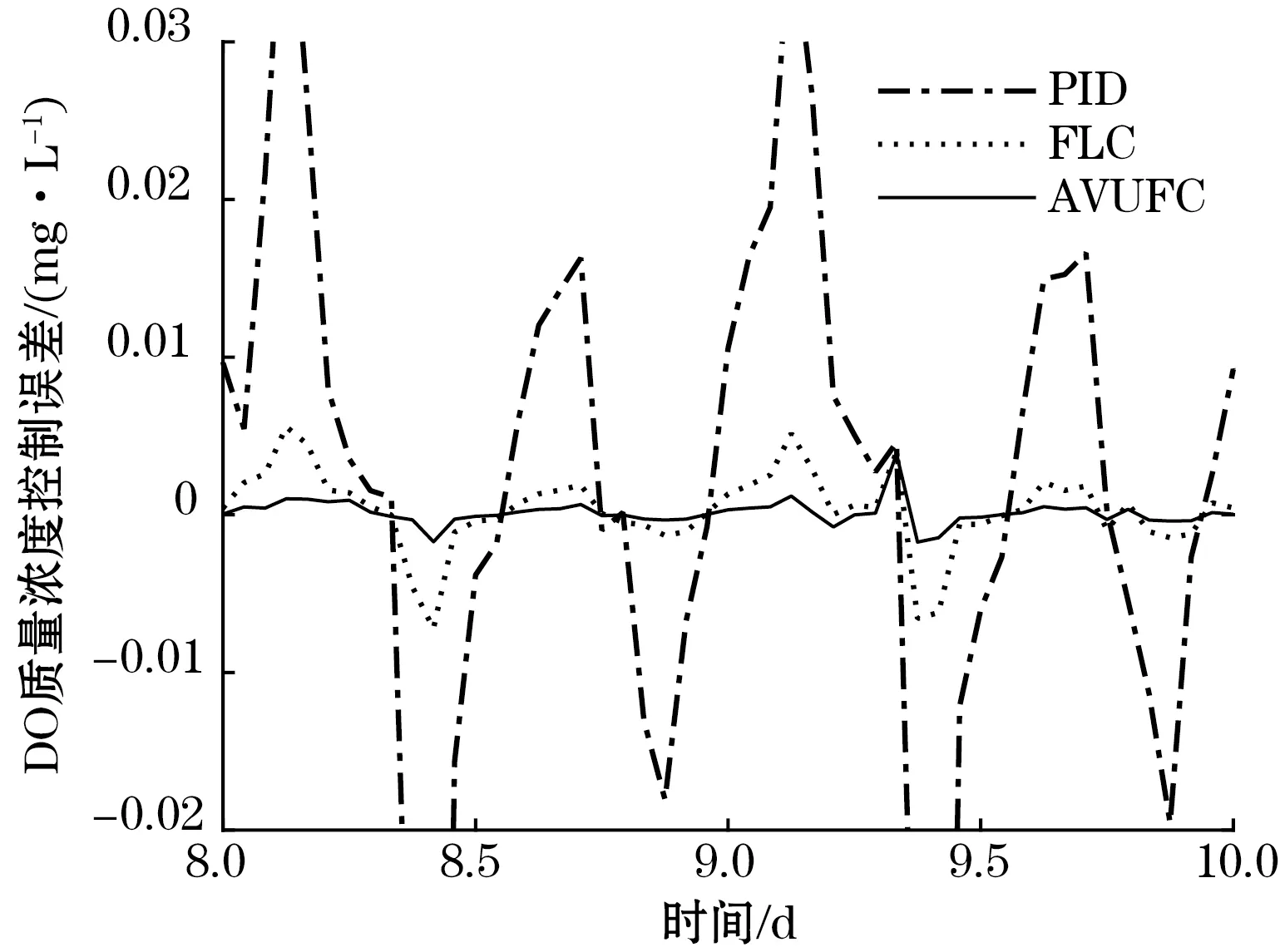
(a)DO的控制误差

表2～表4分别给出了晴好、阴雨、暴雨3种天气下的DO和NN恒定值跟踪控制结果，并将AVUFC的控制效果与PID、FLC和VUFC进行了对比分析。从表2可以看出，对于DO恒定值控制，在晴好天气工况下，AVUFC的IAE仅为0.84，远小于PID的28.84，也小于FLC的3.14和VUFC的1.25，表明AVUFC具有优越的控制性能。分析ISE和DEVmax的实验结果，也能得到类似的结论。因此，可以得到如下结论：本文所提的AVUFC控制策略不仅适用于晴好天气工况，而且在入水流量和水质参数剧烈变化时，也能取得较好的控制效果；本文所设计的自适应模糊规则优化策略，能够更精细地分割输入论域，增强了控制系统的灵活性。

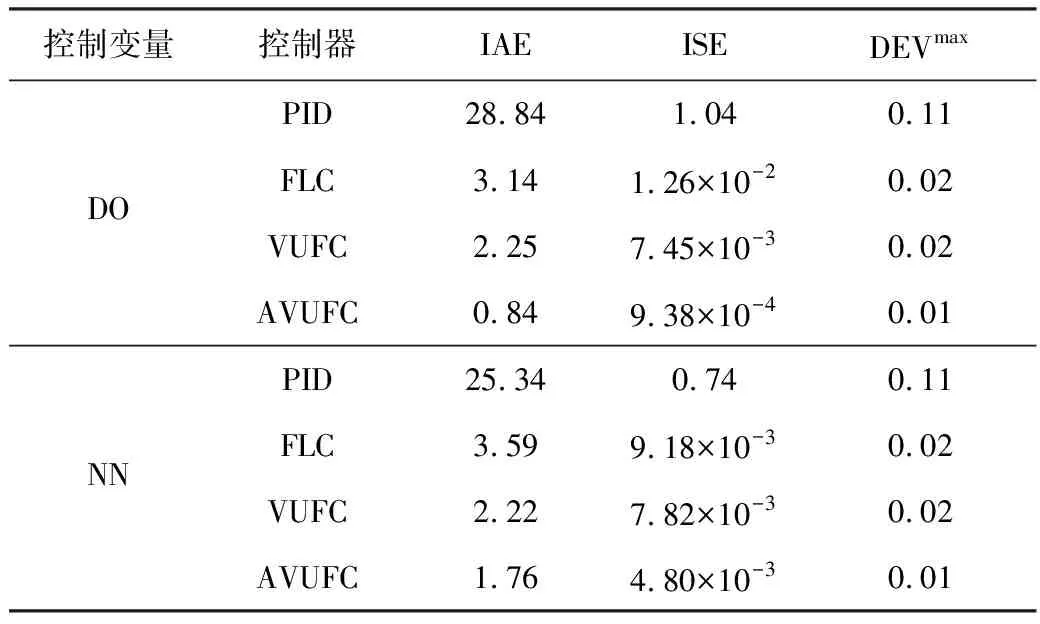
表2 晴好天气下DO和NN恒定值控制结果

表3 阴雨天气下DO和NN恒定值控制结果

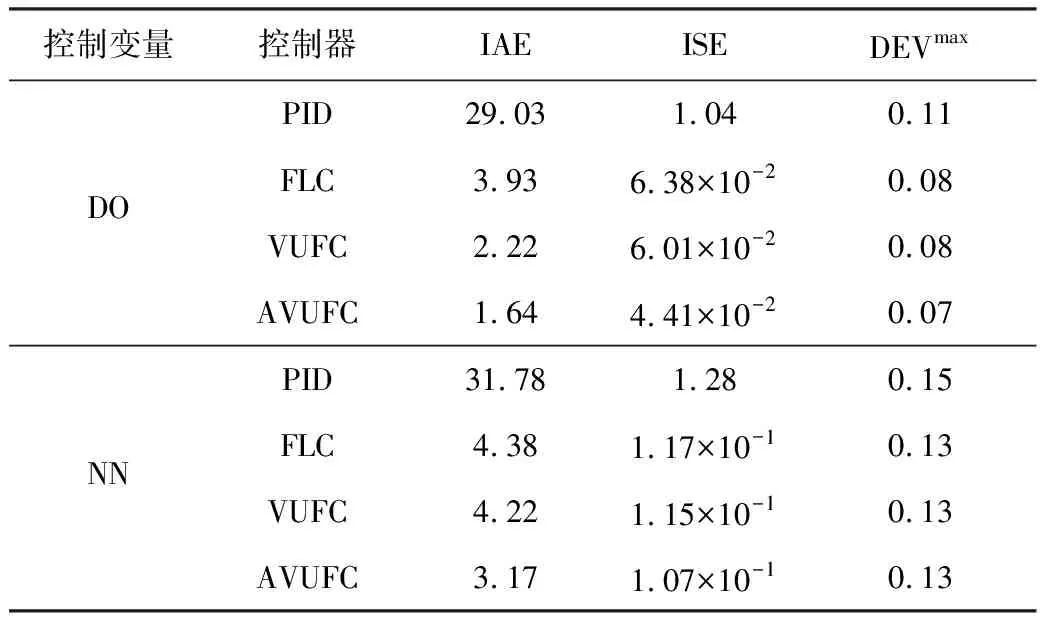
表4 暴雨天气下DO和NN恒定值控制结果

4.4.2 变设定值控制

为了进一步考察控制器的抗干扰性能，DO设定值在1.6～2.4 mg/L之间阶跃变化，NN设定值在0.8～1.2 mg/L之间阶跃变化，利用AVUFC控制器跟踪变设定值。图8～图9分别给出了阴雨天气下PID、FLC、AVUFC的控制效果和跟踪误差。为了清晰展示阴雨天气工况变化的细节，这里只给出了第8～10天的控制结果图。

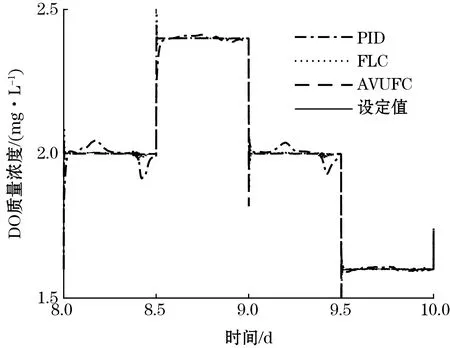
(a)DO的控制效果

从图8可以看出，AVUFC的控制效果明显优于PID和FLC，表明本文所提控制策略的稳定性好、抗干扰性强。从图9可以看出，AVUFC的控制误差明显小于PID和FLC，具有较高的跟踪控制精度。

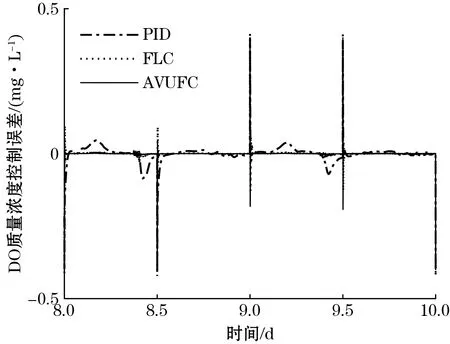
(a)DO的控制误差

表5～表7分别给出了晴好、阴雨、暴雨3种天气下的DO和NN变设定值跟踪控制结果，并将AVUFC的控制效果与PID、FLC和VUFC进行了对比分析。从表5可以看出，对于NN控制，在阴雨天气工况下，AVUFC的IAE仅为6.29，远小于PID的37.67，也小于FLC的8.35和VUFC的7.92，表明AVUFC取得了最佳的控制效果。分析ISE和DEVmax的实验结果，也能得到类似的结论。

因此，分析表5～表7，可以得到如下结论：本文所提的AVUFC控制策略不仅适用于恒定值控制，而且在变设定值控制时也能表现出优越的控制性能；本文所设计的自适应模糊规则优化策略，能够在阴雨、暴雨等复杂工况下，在设定值阶跃变化情况下，显著增强控制器的自适应能力和快速响应能力。

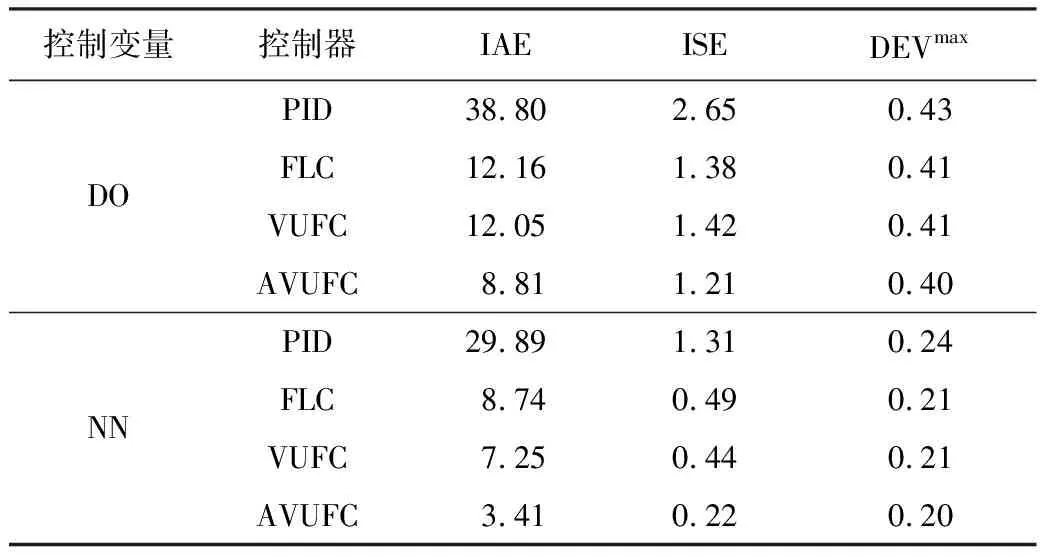
表5 晴好天气下DO、NN变设定值控制结果

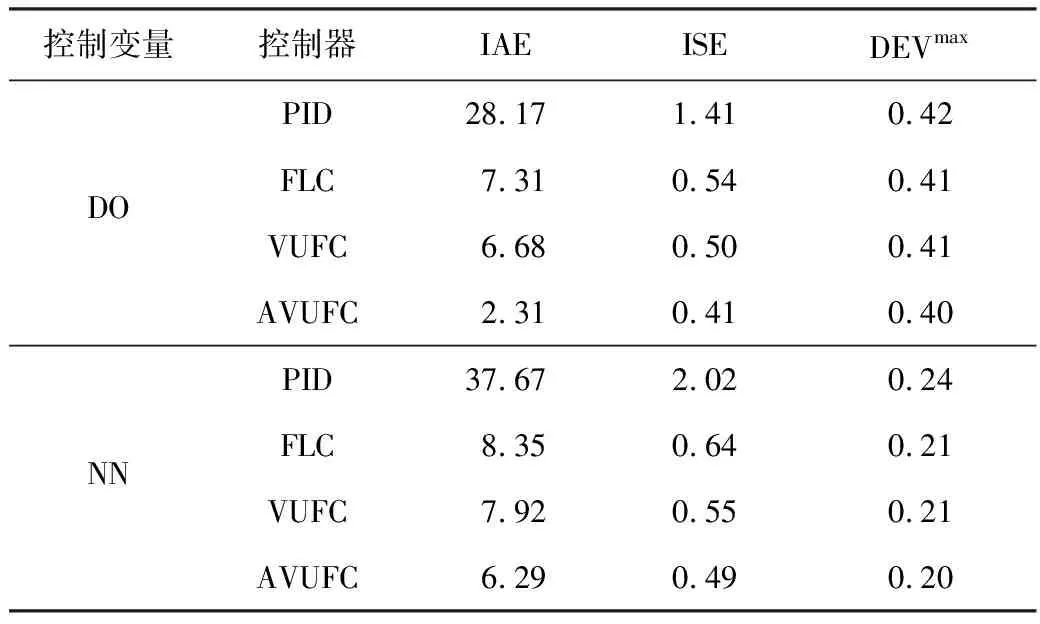
表6 阴雨天气下DO、NN变设定值控制结果

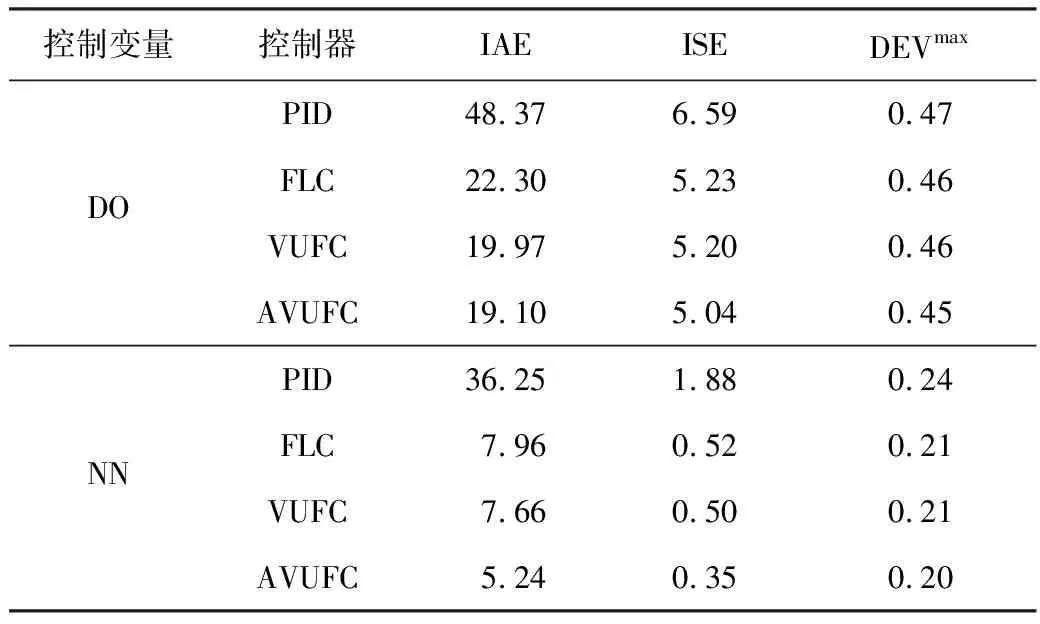
表7 暴雨天气下DO、NN变设定值控制结果

5 结束语

针对活性污泥污水处理过程溶解氧和硝态氮浓度难以控制的问题，提出一种自适应变论域模糊控制策略(AVUFC)。在AVUFC中，设计了一种基于协同自适应策略的差分进化算法，能够实时优化输入输出变量的伸缩因子，从而实现输入输出变量论域范围的动态调整，提高了控制精度。利用BSM1基准仿真平台验证所提算法的性能，针对晴好、阴雨、暴雨3种不同天气工况，设计了恒定值控制和变设定值控制2种控制范式，将AVUFC控制效果与PID、FLC等进行了对比分析。实验结果表明，通过规则库的自适应调整，AVUFC控制器能够较好地适应具有非平稳、不确定性、大时变特征的污水处理复杂工况环境，具有较高的精确性、平稳性以及快速响应阶跃变化的能力，在取得令人满意的底层控制效果的同时也降低了运行能耗。