含未知磁滞输入的机械臂系统预设性能控制
杨朋举,刘 烨,黄小刚,王承茂
(上海工程技术大学电子电气工程学院,上海 201620)
0 引言
近几十年来,机械臂因其质量轻、能耗低、灵敏度高等优点而被广泛应用于工业、医疗及航天等领域[1]。目前,学者已提出众多与机械臂相关的控制策略,主要包括反演控制[2]、滑模控制[3]、无源控制[4]和容错控制[5]等。其中反演控制因在非线性项处理方面独具优势,逐渐成为设计非线性系统控制器的有力工具,但因其需对虚拟控制率反复求导而促使系统微分项不断膨胀,最终导致复杂性爆炸问题。为解决该问题,文献[6]提出利用一阶滤波器估计虚拟控制率导数的动态面控制策略,极大降低了控制器设计难度。在此基础上,文献[7]将该策略应用于含非线性项及扰动的机械臂控制器设计,而文献[8]进一步将未知饱和输入考虑在内,消除了饱和输入对执行器的影响。然而,上述文献均未考虑执行器受其内部磁滞效应的影响。
在实际应用中,磁滞效应广泛存在于工业设备以及物理系统,如继电器[9]、电磁场[10]、含智能材质的传感器[11]以及执行器[12]等。机械臂作为常见的工业设备,其执行器通常因内部存在智能结构而深受磁滞效应影响,这极大影响系统输出精度,甚至导致闭环系统失稳,故消除磁滞效应以提高控制精度成为研究重点。目前,存在2种解决磁滞问题的控制策略:一种是构建磁滞逆过程,并将其级联至系统输入端[13];另一种是采用鲁棒控制策略消除磁滞现象[14]。因磁滞逆构建过程复杂,且其输出量又对内部参数敏感,故上述鲁棒策略更具优势。近年来,学者已采用鲁棒策略提出众多高效方案,并设计一系列磁滞模型,如Bouc-Wen磁滞[14]、PI磁滞[15]和类间隙磁滞[16]等。虽然上述方案能有效消除磁滞特性对系统执行器的影响,但其均致力于改善系统的稳态性能而未考虑瞬态性能问题。
为了确保系统的瞬态性能,文献[17]提出一种预设性能控制策略,通过转换跟踪误差获取新的误差变量,据此设计自适应控制器。在此基础上,文献[18]构造一种新型误差转换函数,并将其应用于机械臂控制器的设计以约束跟踪误差的超调量,但此函数在误差转换时需求逆函数,此时可能导致奇异性问题,促使跟踪误差跃界并造成系统失稳。为了解决该问题,文献[19]使用Funnel变量约束跟踪误差的收敛特性,放宽了对系统阶数的限制,而文献[20]进一步构造新Funnel变量以解决传统Funnel变量的不可微问题。虽然对非线性系统预设性能控制的研究已相当深入,但对机械臂磁滞系统的预设性能动态面控制的研究较少,其难点在于能消除磁滞影响且能确保预设性能的控制器设计。
针对含未知磁滞输入的单连杆机械臂系统,提出一种神经网络动态面预设性能控制策略。对于工业生产中常用的机械臂控制系统,从同时提高其稳态和瞬态性能的角度出发,在其执行器内含智能材料的情况下,仍然能对其保持高精度的控制。利用Bouc-Wen模型描述系统执行器内的磁滞现象,结合自适应技术在线消除磁滞特性的影响;采用动态面策略设计控制器,避免传统反演策略固有的微分膨胀问题,从而极大地降低控制器的设计难度;利用Funnel变量和性能边界函数约束系统位置跟踪误差的收敛特性,确保该误差收敛至预定范围。
1 问题描述
考虑含未知磁滞输入的单连杆机械臂,如图1所示。根据拉格朗日建模方法,其动力学方程[8]为
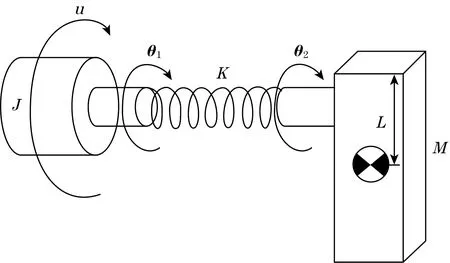
图1 单连杆机械臂
(1)
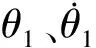
本文选取Bouc-Wen磁滞模型描述机械臂执行器内的磁滞现象,其数学定义[14]为
H(u)=ε*ζ*u+(1-ε*)ζ*ξ*
(2)
式中:ε*为刚度比,0<ε*<1;ζ*为与伪自然频率相关的正参数;ξ*为辅助变量,其导数为
(3)
式中:ϑ*和φ*分别为用于描述滞环形状和振幅大小的设计参数,ϑ*>|φ*|;λ*为滞环曲线的光滑性参数,其能够控制滞环曲线从初始斜率至渐近斜率的过渡光滑性,λ≥1。
该模型滞环特性曲线如图2所示,此时需满足ξ*(0)=0,u(t)=4sin(2t),ε*=0.25,ζ*=15,ϑ*=2,λ*=1和φ*=0.25。
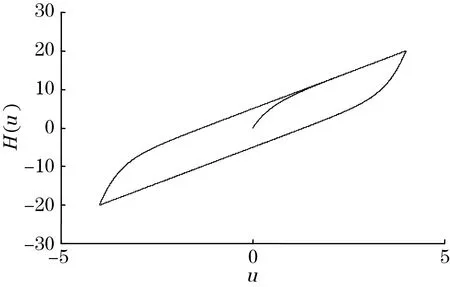
图2 Bouc-Wen滞环特性曲线
(4)
式中y为系统输出。
控制目标是消除未知磁滞输入的影响,确保系统输出跟踪参考轨迹,使闭环系统内全部信号达到半全局有界,并同时改善系统稳态与瞬态性能。为达到此目标,引入如下假设与引理:

引理1[8]:利用径向基神经网络(RBFNN)将定义在紧集内的未知光滑函数f(φ)估计为
f(φ)=W*TΨ(φ)+δ(φ)
(5)

(6)
式中ϑl和ζl分别为节点l的基宽度以及中心向量。

|ξ*(t)|≤max{|ξ*(0)|,1/(ϑ*+φ*)1/λ*}
(7)
式中ξ*(0)是ξ*的初值。
2 动态面控制器设计
动态面控制策略沿用传统递归设计理念,将高阶系统分解为低阶系统,逐步为低阶系统设计虚拟控制率,并使用滤波器估计虚拟控制率导数,最终推出实际控制量。为便于设计,进行如下变换:
(8)
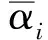
系统控制结构如图3所示。

图3 控制结构图
详细设计步骤如下:
第1步:对位置跟踪误差e1进行变换得到新误差变量z1,其可被称作Funnel变量[20],其定义为
(9)
式中:yd为连杆位置的参考轨迹输出量;Fω为控制系统的性能边界函数,其定义为
Fω(t)=(ρ0-ρ∞)exp(-β*t)+ρ∞
(10)
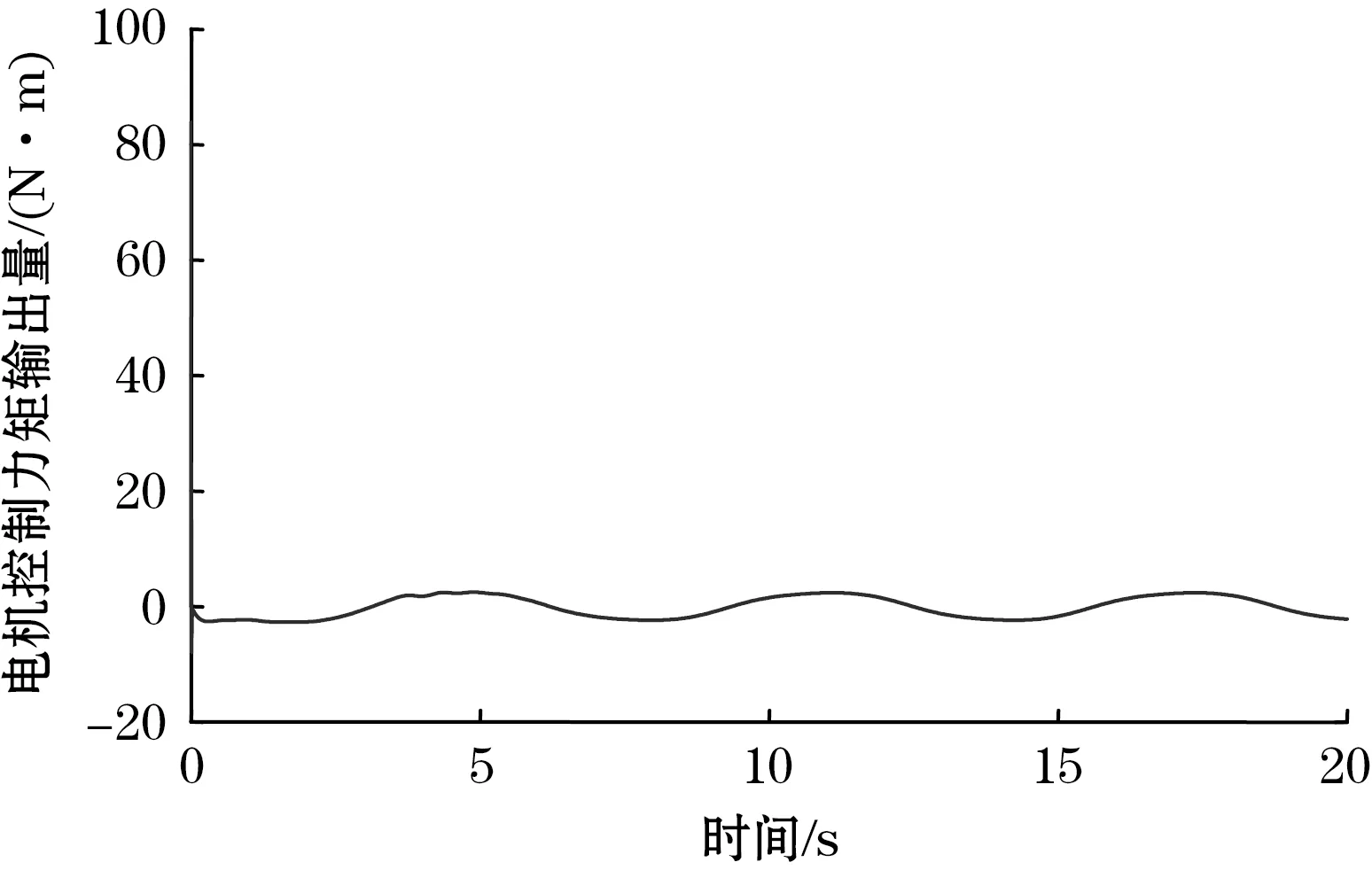
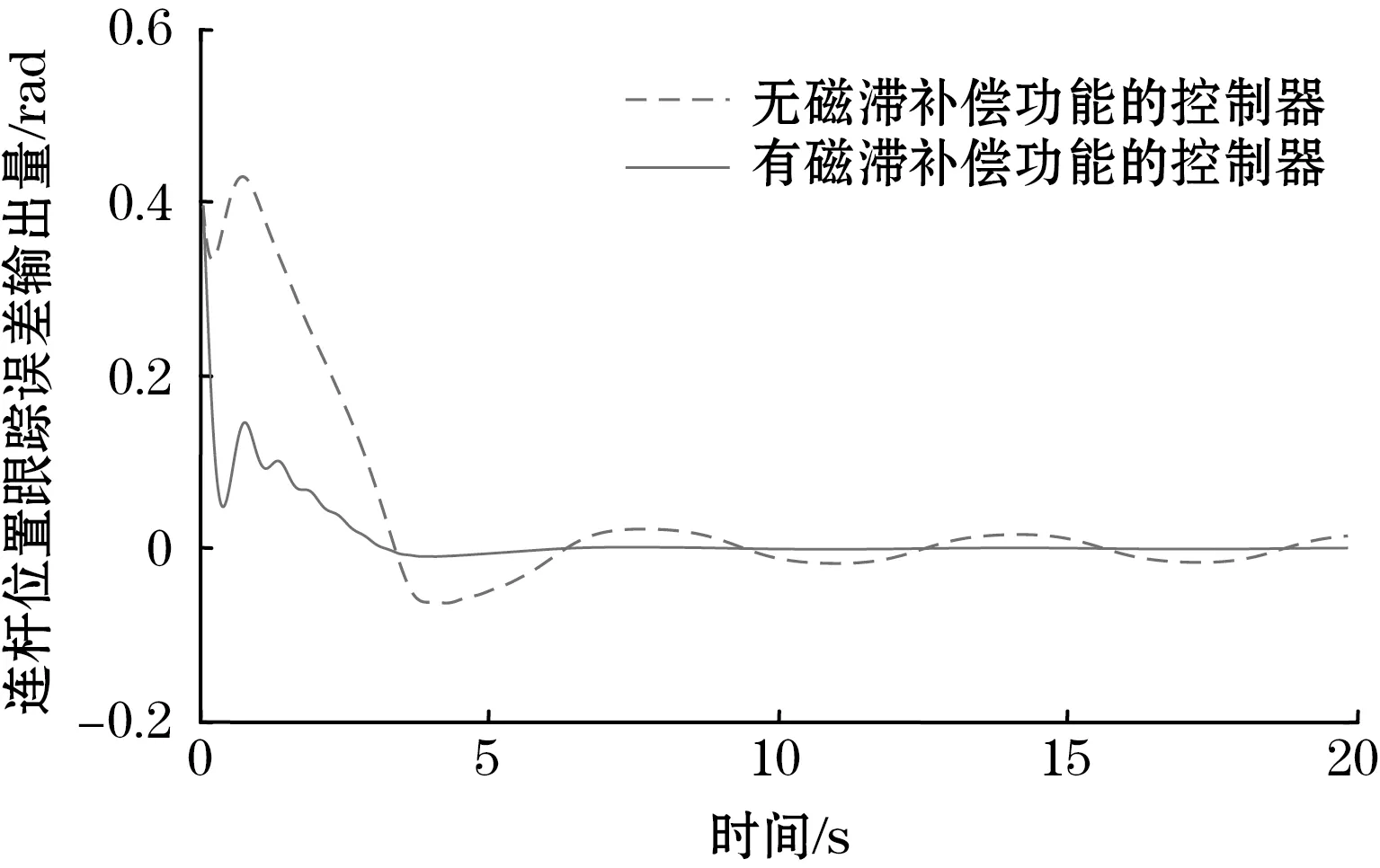
式中:ρ0、ρ∞和β*分别为Fω的初值、终值和指数函数的收敛率;|e1(0)| 根据式(9),得 (11) 将虚拟控制率α1设计为 (12) 式中c1为正设计参数。 为了规避反演法固有的“微分膨胀”问题,利用如下一阶滤波器对α1进行滤波: (13) 式中σ1为时间常数,σ1>0。 根据式(8)和式(13),得 (14) (15) 利用不等式 (16) 并结合式(11)~式(14),对式(15)求导,得 (17) 第2步:根据式(4)和式(8),z2的导数为 (18) 式中:η=K/(ML2);f1(φ1)=-F(x2)/(ML2)。 根据引理1,利用RBFNN将f1(φ1)估计为 (19) 式中:φ1=x2;|δ1(φ1)|≤λ1,λ1为未知正常数。 利用杨氏不等式,得 (20) 将α2设计为 α2=-[c2z2+(η2+1)z2/2-ηx1-gsinx1/L+ (21) 将其自适应率设计为 (22) 对α2滤波,即 (23) 式中σ2为时间常数,σ2>0。 根据式(8)和式(23),得 (24) (25) 利用不等式 (26) 并结合式(18)~式(24),对式(25)求导,得 (27) 第3步:根据式(4)和式(8),z3的导数为 (28) 其次,将该步的虚拟控制率α3设计为 (29) 式中c3为正参数。 对α3进行滤波,即 (30) 式中σ3为时间常数,σ3>0。 根据式(8)和式(30),得 (31) (32) 利用不等式 (33) 并结合式(28)~式(31),对式(32)求导得 (34) 第4步:根据式(4)和式(8),z4的导数为 (35) (36) 利用杨氏不等式,得 (37) 将系统的实际控制量u设计为 (38) 将其自适应率分别设计为 (39) 然后,将该步的Lyapunov函数选取为 (40) 利用不等式 (41) 并结合式(35)~式(39)对式(40)求导,得 (42) 将该方案的稳定性分析以定理形式给出,如下所示: 证明:为了方便分析,不妨令Z=[z1,z2,z3,z4],S=[s1,s2,s3],并定义如下紧集: (43) 式中R0和R1均为正常数。 将整个系统Lyapunov函数选取为V=V1+V2+V3+V4。利用不等式 (44) 结合式(17)、式(27)、式(34)以及式(42)对V求导,令1/σk-1≥0(k=1,2,3),得 (45) 并对式(45)求解,得 0≤V(t)≤υ/(2θ)+[V(0)-υ/(2θ)]exp(-2θt) (46) 其说明整个闭环系统内所有信号均能达半全局有界。 根据式(9)和式(46),得 (47) 表1 机械臂系统参数 仿真结果如图4~图7所示。图4是连杆跟踪参考轨迹的响应曲线。图5是连杆位置跟踪误差及其性能边界的变化曲线。图6是本文控制方案的电机控制力矩响应曲线。根据图4~图5,可见本文预设性能动态面控制器不仅能降低跟踪误差的最大超调量,且能改善系统的稳态性能。为进一步展示本文控制器的抗磁滞性能,在保持现有条件不变的情况下,与无磁滞补偿的控制器对比。仿真结果如图7所示,可见本文控制器能消除执行器内磁滞效应的影响,进而有效改善控制系统的稳态性能。 图4 连杆位置输出量及其参考轨迹 图5 连杆位置跟踪误差及其性能边界 图6 电机控制力矩 图7 连杆位置跟踪误差 针对含未知磁滞输入的单连杆机械臂系统,本文提出一种神经网络预设性能动态面控制方案。首先利用磁滞模型描述系统执行器内的未知磁滞现象,其次利用神经网络逼近系统内的未知函数,同时利用Funnel变量和性能边界函数约束跟踪误差最大超调量,据此采用动态面策略设计控制器。结果表明该控制器能使闭环系统内全部信号达半全局有界,并能保证跟踪误差的预设性能。仿真结果显示此方案能有效消除磁滞效应对系统执行器的影响,并能同时改善系统的稳态及瞬态性能。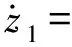
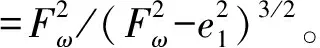
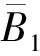
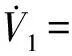



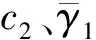
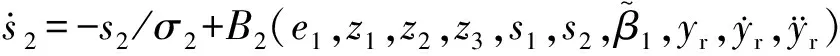
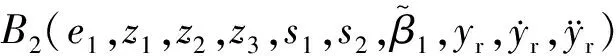
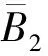
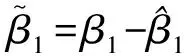

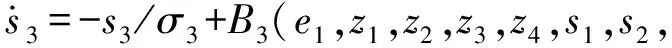
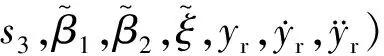
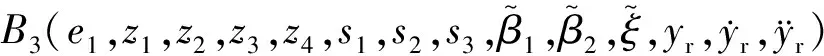

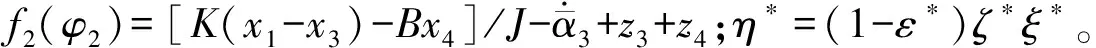





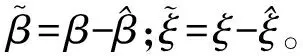
3 稳定性分析


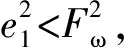
4 仿真研究



5 结论

