基于加权最小二乘法的分数延时滤波器设计

林文涛，贾玉博，张紫文，胡 忞，易朋兴

(华中科技大学机械科学与工程学院，湖北武汉 430074)

0 引言

可变分数延迟(VFD)滤波器在数字信号处理中有着广泛的应用，例如任意采样率转换、分数阶微分器设计、数字波束形成[1-2]。现有的VFD FIR滤波器算法可分为2类:时域插值算法和频域优化算法。时域插值算法基于多项式插值，如Lagrange、b样条、Hermite[3-4]等。时域插值虽然计算简单，但在高频下的响应较差。相比之下，通常采用频域优化的方法来设计在大带宽下具有足够响应的VFD FIR滤波器。常用的优化准则包括最大平坦(MF)[5]、加权最小二乘(WLS)[6]和极大极小准则(MM)[7]。加权最小二乘法(WLS)通过求解线性方程得到滤波器系数，极小极大(minimax)方法过将传输特性与期望值间的最大幅度误差最小化获取滤波器系数。综合考虑精度和运算复杂性，选择加权最小二乘法来配置滤波器系数。

1 Farrow结构分数延时滤波器原理

理想的可变分数滤波器的频率响应[8]为

HD(ω，p)=e-jωp=cos(ωp)-jsin(ωp)，

ω∈[-ωp,ωp]，p∈[-0.5,0.5]

(1)

式中：ω为归一化角频率；p为滤波器分数延时。

设计实际的滤波器则需找到一个传递函数来逼近理想的频率响应，这个传递函数可表示为[9]

(2)

式中：z为频率响应参数；p为分数延时参数；n为滤波器阶数。

hn(p)可表示为p的M阶多项式：

(3)

式中m为滤波器个数。

因此，实际传递函数可表示为：

(4)

(5)

其频率响应为

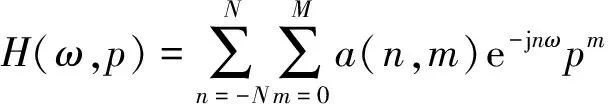
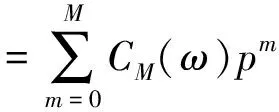
(6)

因此VFD滤波器的设计转化为如图1所示的M+1个滤波器系数求解问题。这便是Farrow结构滤波器，其系数是由时延p的M阶多项式构成[10]。

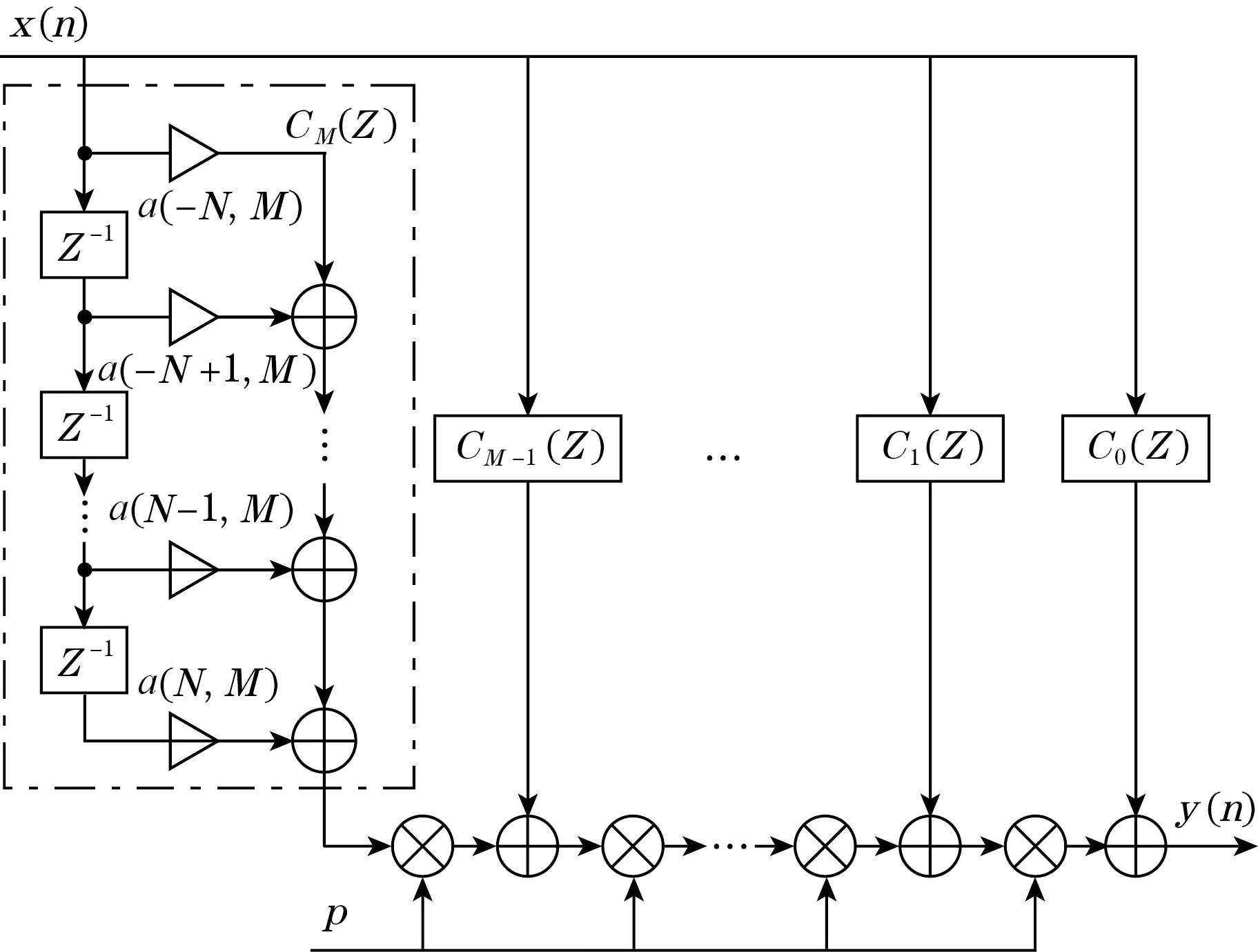
图1 基于Farrow结构VFD滤波器

对于滤波器系数的配置，可以采用加权最小二乘法(WLS)实现，该过程中权重是关于ω和p的函数，通过绝对误差，分别选择对应变量不同范围内的权重值，运算的复杂程度较高，得到不同频率响应误差总能量最小。误差函数权重与p的关联的影响可暂时忽略，依然能获得较好的特性曲线，即最小二乘法中权重是ω的非负权重函数W(ω)，且W(p)≡1，这样便能简化推导过程。此外，利用滤波器系数的对称性和系数约束关系能够缩小权重函数积分范围，即ω∈[0,ωp]，p∈[0,0.5]，相关研究也证明这种推论是成立的[11]。

2 分数延时滤波器设计

2.1 滤波器系数求解

运用加权最小二乘法来求解滤波器系数实际上是理想滤波器与设计滤波器的加权平方误差函数E(ω,p)求取最小值的过程[12]。

(7)

利用滤波器系数的对称性：

a(-n,m)=(-1)m·a(n,m)

(8)

式(6)可转化为2个子函数之和:

(9)

通过欧拉公式展开得：

(10)

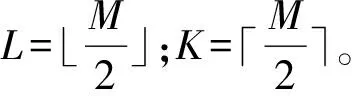
当滤波器的群延时p取0代入式(1)及式(10),得:

HD(ω,0)=1

(11)

(12)

假设式(12)中，a(0,0)=1,a(n,0)cos(nω)=0,则

(13)

设计滤波器的频率响应进一步转化为：

(14)

(15)

式中：

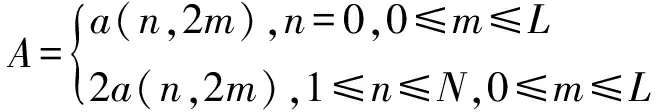
B=-2a(n,2m-1),1≤n≤N,1≤m≤K

(16)

将加权平方差函数E(ω,p)离散化表示：

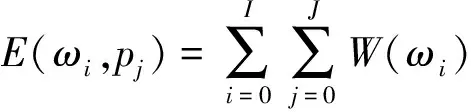
(17)

式中：I、J为ω,p的离散化步长数。

ωi=i·ωp/I

pj=0.5j/J

将式(1)、式(15)代入式(17)得

(18)

为简化计算，将式(18)转换成矩阵形式:

E(A,B)=tr[(TE-CAPET)T(TE-CAPET)]+

tr[(TO-SBPOT)T(TO-SBPOT)]

(19)

式中tr[·]表示矩阵的迹，其各个矩阵表示为：

(20)

(21)

(22)

(23)

(24)

(25)

将式(19)对矩阵A与B分别求偏导，值为0便得到最小的平方误差：

(26)

由式(26)可得

(27)

矩阵A与B的各元素代表偶数与奇数位置子滤波器CM(z)对应位置的系a(n,m)。

2.2 加权系数迭代求解

解得滤波器系数之后便可计算其幅度响应的绝对误差：

e(ω,p)=|HD(ω,p)-H(ω,p)|

(28)

通过改变权重函数W(ωi)的值进而得到不同的滤波器系数，滤波器幅度响应最大绝对误差也随之改变。为了进一步减小滤波器幅度响应的最大绝对误差，引入一种迭代判断方法来调整权重函数。

具体实现流程如下：

(1)取初始权重函数W1(ωi)=1,0≤i≤I，解得第一代滤波器系数a1(n,m)，并计算幅度响应绝对误差e1(ωi,pj)；

(2)寻找到最大绝对误差下的群延时pm，之后每次迭代都将使用该值作为寻找不同权重下最大绝对误差；

δk(pm)=max{ek(ωi,pm)}

(29)

(3)取极小正数ε(例如ε=1×10-5)，将ek(ωi,pm)与ε进行比较。若ek(ωi,pm)≥ε，则

(30)

若ek(ωi,pm)<ε,则

Wk(ωi)=Wk-1(ωi)

(31)

(4)在新的权重函数下计算滤波器系数，计算得δk(pm)，并计算：

(32)

(5)若εp≤ε，则迭代停止，反之返回步骤(3)进行多次迭代。

3 滤波器仿真测试

为验证上述滤波器设计的合理性，设定参数N=33、M=7、ωp=0.9π、I=40N、J=100、W(ω)=1。将以上参数代入上述公式中求解矩阵A、B得到滤波器系数，并计算其幅度响应的最大绝对误差来评判所设计滤波器的性能。

εm=max|HD(ω,p)-H(ω,p)|，0≤ω≤ωp,0≤p≤0.5

(33)

εH=20 lg εm

(34)

在第一次迭代中，发现pm=0.5，εm=3.154 9×10-5,εH=-90 dB。将pm代入式(30)重新计算权重函数值并进行多次迭代直至循环结束，εm=1×10-5，εH=-100 dB。图2～图3为初次迭代时实际滤波器与理想滤波器的幅值误差，图4～图5为迭代结束实际滤波器与理想滤波器的幅值误差。

图2 初始可变分数延时绝对误差

图3 初始可变分数延时绝对幅度误差

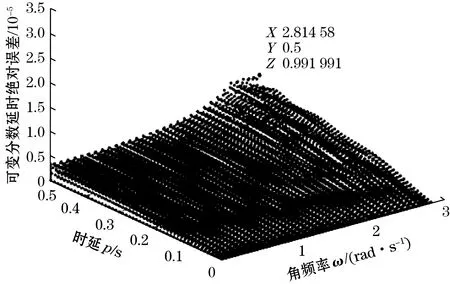
图4 迭代后可变分数延时绝对误差

图5 迭代后可变分数延时幅度绝对误差

如图6所示，迭代20次之后趋于平稳，最大幅度绝对误差减小了10 dB。相较于参考文献[12]，当p=0.22，ω=0.88π时其滤波器延时误差为5.495 4×10-6,幅度误差为-105.2 dB;本文所设计的滤波器延时误差为1.578 6×10-6，幅度误差为-116.0 dB，滤波器的性能有所提升。

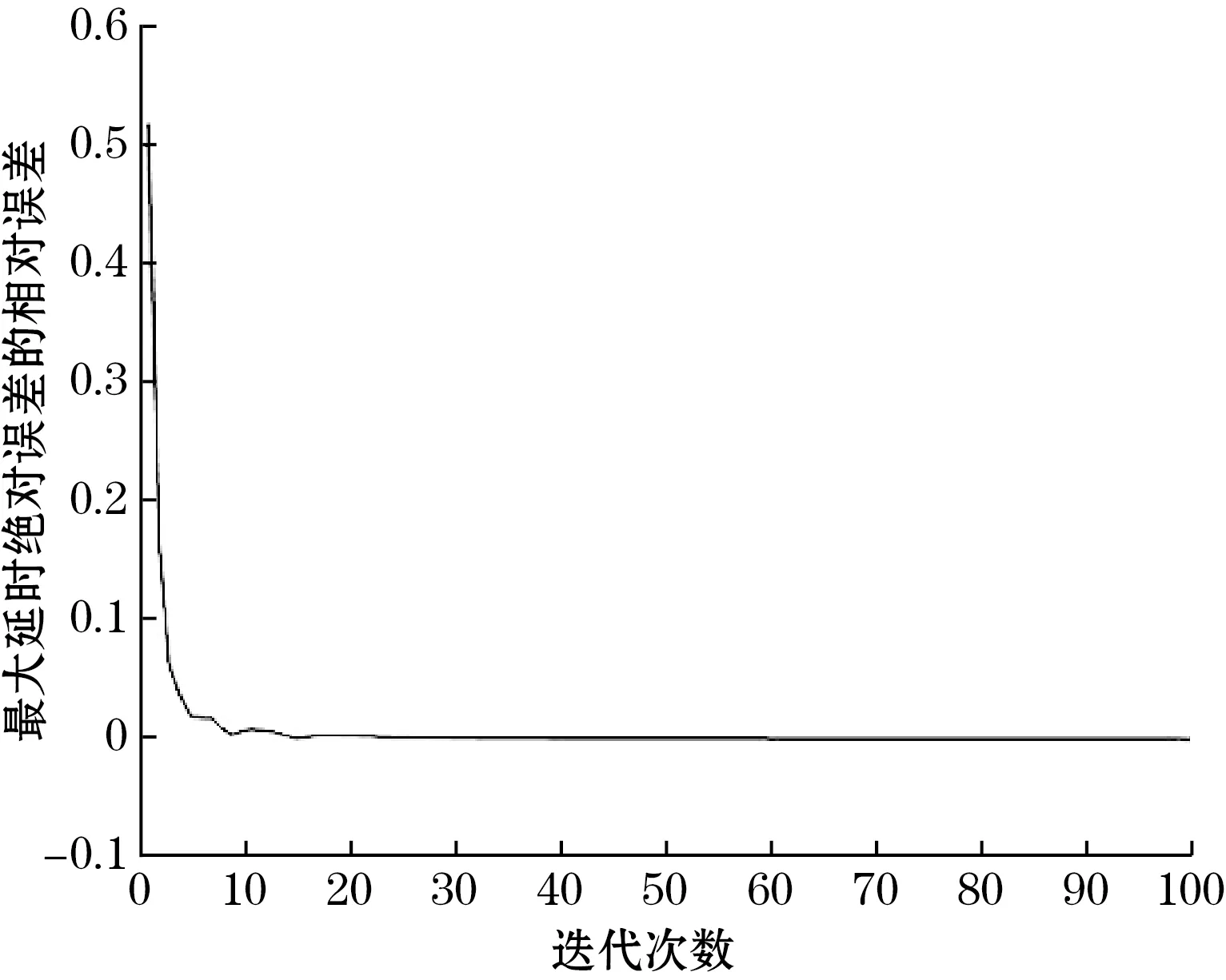
图6 相对误差迭代轨迹

4 结束语

基于加权最小二乘法提出了一种Farrow结构可变分延时滤波器的设计方案及相应的加权函数系数迭代求解方法。将加权平方差函数离散化则不需进行数值积分或求解闭式公式，简化滤波器系数的求解；通过迭代后的加权函数系数来优化滤波器系数，使滤波器性能更加接近理想滤波器。经过理论分析与仿真验证，所设计的滤波器性能良好，迭代算法收敛迅速。