带相移的离散时间相耦合振子系统的同步
张 华,肖斯斯
(重庆理工大学 理学院, 重庆 400054)
0 引言
相耦合Kuramoto振子系统的同步现象,比如渐近同步[1]、爆炸性同步[2-3]、分群同步[4]、有限时间同步[5-6]和固定时间同步[7]等,在过去几十年受到了世界范围内众多学者的广泛关注。该网络系统作为一个经典模型能很好地刻画和描述来自生物学[8]、化学[9]、经济学[10]到工程学[11]、社会学[12]、地震学[13]等不同学科中的群集动力学行为。诸如心脏起搏器单元、脑神经元、平面车辆协同、萤火虫集群、鳗鱼中枢神经系统、半导体激光器、微波振荡器等均为该模型在实际生活中的典型应用[14-15]。相耦合振子系统通常由大量的同质或异质振子以及表述振子之间相互作用的网络拓扑图构成,其异质性和网络特性常使得该系统呈现出丰富的动力学行为[16-21]。
含有N个相耦合振子系统的一般动力学方程通常可以表示为
(1)
式中:变量θi(t)表示第i个振子的相位状态,ωi为自然频率,aij表示振子i和j之间的耦合关系,如果i和j之间有相互作用,那么aij>0,否则aij=0。
相耦合模型的力学模拟弹簧质点网络系统[15],如图1所示。该网络由大量在单位圆上运动且互不碰撞的粒子构成,τi为外部驱动扭矩,kij为弹簧的刚度系数。除力学模拟之外,在振荡电路、电网、自驱车辆、社会网络中观点同步[22]等应用中均有类似方程(1)的动力学方程。

图1 耦合振子系统的力学模拟示意图
在经典相耦合振子系统的相互耦合作用中引入相移可以描述更加丰富的动力学行为。例如,文献[23]研究了带有时滞和相移效应的振子同步群集行为,该模型中时滞为零时即为带有相移的连续时间型Kuramoto振子模型,其动力学方程为:

(2)
式中:λ为耦合强度,γ为相移。此类模型具有广泛的实际应用。例如,由3个带相移的且非恒同的振子系统构成的模型可用于研究太阳深部经络环流的重建及其在太阳发电机方面演化的作用[24]。
带有相移因素的模型在理论方面同样具有重要的研究意义。例如,基于Watanabe-Strogatz (WS) 变换,文献[25]针对一种广义Kuramoto系统,提出了如何确定该WS变换系统初始值的方法,研究了WS变量的渐近行为,给出了带相移的Kuramoto振子系统的定量渐近行为,并得到了达到相位或频率同步的一些充分条件。此外,还有带随机相移的振荡器网络同步[26]、带相移和惯性作用的振子锁相态唯一性和有序性[27]等研究报道。
以上关于相耦合振子系统的建模,大都集中在振子之间的连续相互作用方面,而针对时间离散型的研究相对较少[28-33]。例如,文献[33]给出了在离散时间步长趋于零时,系统的稳定性可以转化到连续时间型系统的稳定性分析方法。值得注意的是带有相移因素的离散时间耦合振子系统的相位同步和频率同步研究鲜有报道。鉴于此,建立了一种带有相移因素的离散时间耦合的Kuramoto振子模型,给出了含有相移的离散时间型振子系统的相位同步和频率同步的充分条件。最后,计算机数值模拟进一步验证了所得充分条件的正确性。
1 模型描述
对式(2)两边求导,得
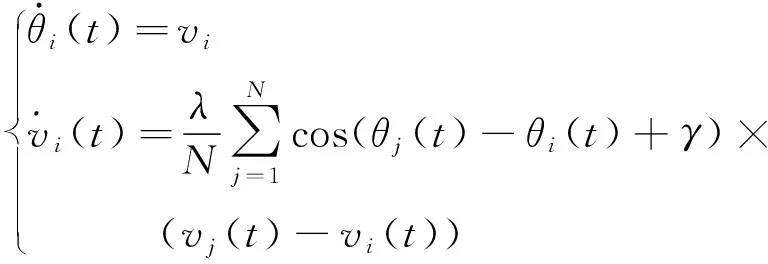
(3)
然后对式(2)和式(3)分别按照时间变量离散化,得
(4)
以及
(5)
这里,θi(k)=θi(tk),vi(k)=vi(tk)为tk处的频率,时间步长h=tk-tk-1>0,k=0,1,2,…。

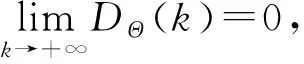


2 相位同步
首先讨论系统(4)在振子频率恒同的情况下系统的相位同步问题。
定理1对于恒同振子,即ωi=ω,若hλ<2,DΘ(0)
证明对任意k,令c=max{|1-hλ|, |1-hλcos(b+γ)|,|1-hλcos(γ-b)|}<1,首先证明如下不等式:
DΘ(k+1)≤cDΘ(k) (6) 不失一般性,假设θM(1)、θm(1)分别表示k=1时的最大值和最小值。因为DΘ(0) sin(θj(0)-θm(0)+γ))= (θM(0)-θm(0))-hλcos(ξj,0)× (θM(0)-θm(0))≤ |1-hλcos(ξj,0)||θM(0)-θm(0)|≤ cDΘ(0) 式中:ξj,0介于θj(0)-θM(0)+γ和θj(0)-θm(0)+γ之间。 由数学归纳法,假设不等式DΘ(k)≤cDΘ(k-1) 下面讨论系统(5)的频率同步问题。为方便模型分析,对参数γ、h、λ以及直径D(Ω)和DΘ(0),作如下假设: 假设1设常数l、α、β、p、μ满足以下条件: l=min{π/3-γ, π/3+γ} (7) hD(Ω)≤α<(1-p)β<π/2,p∈[1/3,1) (8) α+(2+p)β≤μ (9) DΘ(0)≤l (10) 2(1-p)≤λh≤1+p (11) 在下面给出如下关于振子相位差的一个重要性质。 定理2若γ∈(-π/3,π/3),那么在假设1的条件下,系统(4)或(5)的相位满足如下结论: 1)DΘ(k)≤l≤π/3,k=0,1,2,… (12) (13) 式中:「x⎤表示对x取整,且「x⎤≥x。 证明首先由式(10)有DΘ(0)≤l,由数学归纳法,假设不等式DΘ(k)≤l成立。令θM″(k+1)、θm″(k+1)分别表示Θ在k+1处的最大值和最小值,θM′(k)、θm′(k)分别表示在k处的最大值和最小值。那么由拉格朗日中值定理得 DΘ(k+1)-DΘ(k)=θM″(k+1)-θm″(k+1)-θM′(k)+θm′(k)≤hD(Ω)+ sin(θj(k)-θm″(k)+γ))-θM′(k)+ θm′(k)+θM″(k)-θm″(k)= hD(Ω)+(hλcos(φj,k)-1)× (θm″(k)-θM″(k))-θM′(k)+θm′(k)≤ hD(Ω)+pDΘ(k)-DΘ(k)= hD(Ω)+(p-1)DΘ(k) (14) 式中:φj,k介于θj(k)-θM″(k)+γ和θj(k)-θm″(k)+γ之间。又因为DΘ(k)≤l,故φj,k∈(-DΘ(k)+γ,DΘ(k)+γ)⊂[-π/3,π/3],进而有cosφj,k∈[0.5,1],又2(1-p)≤hλ≤1+p,故|hλcosφj,k-1|≤p。由式(14)得 洪泽湖现状兴利水位13.0 m,死水位11.30 m,2012年确定其旱限水位为11.80 m。根据《江苏省流域性、区域性水利工程调度方案》中有关洪泽湖水源调度要求、省供水范围的供水调度计划及当时雨水情、用水形势,确定省管及其他重要引水口门的出湖流量。在遭遇干旱年份,为确保城乡生活等重点用水,需要采取江水北调、挖掘死库容等措施。在不影响防洪和排涝的前提下,洪泽湖可在后汛期根据雨水情适时拦蓄尾水,逐步由汛限水位抬高至汛末蓄水位13.0 m,充分利用洪水资源。 |DΘ(k+1)-DΘ(k)|≤hD(Ω)+ |hλcos(φj,k)-1||θm(k)-θM(k)|+ |θM′(k)-θm′(k)|≤ hD(Ω)+(p+1)DΘ(k) 若DΘ(k)≥β,由式(8)可得 DΘ(k+1)-DΘ(k)≤hD(Ω)-(1-p)DΘ(k)≤ α-(1-p)β<0 DΘ(k+1)≤DΘ(k)+|DΘ(k+1)-DΘ(k)|≤ hD(Ω)+(p+2)DΘ(k)< α+(p+2)β≤l 因此,由数学归纳法,式(12)得证。 接下来证明式(13)。首先证明如下结论:若DΘ(K)<α+(p+2)β,则对任意的∀k≥K有 DΘ(k)<α+(p+2)β (15) 按照式(12)的证明方法,即可说明式(15)的正确性。只需要证明 DΘ(K0)<α+(p+2)β (16) 即可证明式(13)成立。因为当DΘ(k)≥β时,由式(14),可知DΘ(k)至少以(1-p)β-α的比率递减,所以存在K1,当 (17) 且k=K1时,有DΘ(k)<α+(p+2)β。 故由式(15)可知,无论DΘ(k)≥β还是DΘ(k)<β,总有DΘ(K0)<α+(p+2)β,证毕。 于是,基于定理2可得系统(5)达到频率同步的一个充分条件。 证明对于某i,j,由式(5)可知 vi(k+1)-vj(k+1)=(vi(k)-vj(k))+ θj(k)+γ)(vq(k)-vj(k)) (18) 对上式两边平方得 (vi(k+1)-vj(k+1))2=(vi(k)-vj(k))2+ E1+E2 式中: (vq(k)-vi(k))-cos(θq(k)-θj(k)+γ)× (vq(k)-vj(k))) 以及 (vq(k)-vi(k))-cos(θq(k)-θj(k)+γ)× (vq(k)-vj(k)))2 由定理2,有 θi(k)+γ)-cos(θq(k)-θj(k)+γ))× (vq(k)-vj(k))+cos(θq(k)-θi(k)+γ)× (vq(k)-vj(k))+cos(θq(k)-θi(k)+γ)× (19) 式中:η为θq(k)-θi(k)+γ和θq(k)-θj(k)+γ之间的一个常数。然后由引理1得 (vq(k)-vi(k))-cos(θq(k)-θj(k)+γ)× (vq(k)-vj(k)))2≤ |vq(k)-vj(k)|)2 (20) 由式(19)和(20)得 |vq(k)-vj(k)|)2 (21) 对上式两边同时关于i、j求和得 |vq(k)-vj(k)|)2= (1-hλ+2hλDΘ(k)+4(hλ)2) × (22) 因此,有 (1-hλ+2hλDΘ(k)+4(hλ)2)k-K0× 由式(8)、定理2以及hλ<(1-2μ)/4,有1-hλ+2hλDΘ(k)+4(hλ)2<1,故有 本节用含有10个Kuramoto振子的系统验证所得相位同步和频率同步理论结果的正确性。首先模拟系统(4)的相位同步,相关参数设置如下:步长h=0.02,耦合强度λ=0.5,自然频率ωi=0.5,i=1,2,…,10,相移γ=π/3,ε=0.001,相位初值Θ(0)= [0.001,π/20,π/18,π/16,π/15,π/14,π/13,π/12,π/10,π/8,π/6]Τ,则初始相位直径DΘ(0)=π/6-0.001。容易验证这些参数满足定理1的条件,振子的相位时间反应曲线如图2所示。相位最大值和最小相位之差在t=20 s时为0.003 6,其状态曲线渐近衰减趋势如图3所示,可见系统(4)相位能渐近达到同步。 图2 振子相位的时间反应曲线 图3 振子相位最大值与最小值之差曲线 对于系统(5)的频率同步设定如下参数:步长h=0.01,耦合强度λ=40,相移γ=π/4,振子的自然频率和初始相位值分别设置为Ω=[0.02,0.1,0.16,0.04, 0.14,0.2,0.4,0.6,0.8,1.02]Τ,Θ(0)=[0,π/20,π/19,π/18,π/17,π/16,π/15,π/14,π/13,π/12]Τ,则DΘ(0)=π/12,D(Ω)=1。常数p=0.8,α=0.01,β=0.075,μ=π/13。可以验证以上参数满足定理2和定理3的条件,系统(5)中振子的相位和频率的时间反应曲线如图4和图5所示。振子频率最大值与最小值之差的渐近衰减效果如图6所示,在时间t=0.3 s时,该差值可以达到4.066×10-5。表明振子的频率最终可渐近同步到一个稳定值。 图4 振子相位的时间反应曲线 图5 振子频率的时间反应曲线 图6 振子频率最大值与最小值之差曲线 主要研究了带有相移的离散时间型相耦合Kuramoto振子系统达到同步问题,分别给出了系统达到相位同步和频率同步的充分条件。通过分析同一时刻任意2个振子相位差的最大值趋于零时所需条件,给出了该系统达到相位同步的充分条件。在证明频率同步时,通过设置某一时刻任意2个振子的相位差的上限值,得到了振子相位差的一个有界性质,然后利用这个有界性证明了该模型的频率同步性。最后数值模拟进一步验证了最大相位差和最大频率差的渐近衰减性和有关充分条件的正确性。

3 频率同步



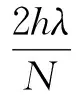


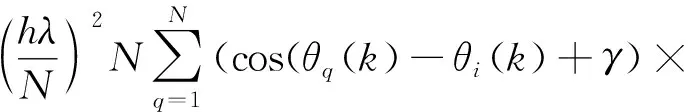



4 数值模拟





5 结论

