面向微振信号的驻极体减振俘能装置设计与建模1)
刘国平 杨朝舒 何忠波,3) 周景涛 孙民政
* (陆军工程大学石家庄校区车辆与电气工程系,石家庄 050000)
† (中国航天员科研训练中心人因工程国家级重点实验室,北京 100094)
引言
随着航天技术和精密工业的发展,微振动条件下隔振减振技术越发受到广泛关注.例如,空间站的微振环境会对各部件的运行及配合造成影响,严重的情况下可能危及其在轨飞行安全;广泛而长期存在的微振环境造成的噪声甚至可能干扰航天员日常工作交流,潜在的微振动影响也可能对相关科学实验的开展和精度控制带来不利影响[1-2];大型空间望远镜的微振动将影响其光轴指向稳定度,造成图像抖动、降低成像质量[3].然而,传统减振隔振技术多采用阻尼结构耗散系统振动能量,这种方式依赖于材料的变形或液体的流动,对加速度量级较低的低频微振动信号并不敏感.相较于一般振动形态,上海航天技术研究所董瑶海[4]总结了航天器微振动具有幅值小、抑制难、频谱宽、固有性等特点,并针对风云四号卫星的微振动环境,提出了振源隔离和载荷隔振的双级隔振系统[5].中国空间技术研究所Li等[6]总结了微振动抑制的三种方式: 扰动源隔振、传递路径隔振和有效载荷隔振.中国科学院大学于济菘[7]提出了对日定向太阳翼振动抑制和地面仿真实验方法,秦超[3]提出了应用空间望远镜的主动阻尼抑振技术.传统的减振隔振技术只能将振动能量以热能形式耗散,无法进一步加以利用,造成了能量的浪费.
近年来,振动俘能技术的发展为微振动控制提供了新思路[8].振动俘能技术通过特定结构,将振动能量收集转换为电能,可用于驱动其他电子元件,或者实现自传感等[9-10].随着MEMS 技术和无线传感器的飞速发展,电子元件的供能需求由原先的高功耗、“聚”分布,转变为了低功耗、“散”分布.为适应供能需求的深刻变化,各类新型无线供电方式蓬勃发展,振动能量回收因来源广泛、收集容易,有望成为传统电池供能的有效替代并减弱振动对原结构的影响[11-14].我国学者开发了电磁式振动俘能机构[15],进行了理论和实验研究,设计了几何非线性结构[16]和双稳态非线性能量阱[17]以提升低频减振俘能性能,在此基础上,发展了压电和电磁耦合的减振俘能器[18].上海大学的赵龙等[19]设计了一种运用于低频振动隔离和能量采集的双功能超材料,实现了振动隔离和能量采集的统一.北京工业大学曹东兴等[20]开发了适用于低频的新型双压电晶片悬臂梁俘能器,并设计了宽频负刚度隔振装置,在低频环境实现了振动能量回收[21].奥克兰大学Hu 等[22]提出了一种改进的超材料梁,用于同时进行振动抑制和能量收集,并开发了分别提升减振和俘能性能的两种模型.Mofidian 等[23]提出一种适用于低频的振动隔振俘能装置,该装置在频率12.5 Hz、加速度1g的振动环境中,俘能功率为0.115 mW.上述学者等在减振俘能领域开展了大量工作,相关研究拓展到非线性[8,24]、上变频[25]等方面,并开发了许多精巧的结构[14,26-27].但受限于大结构尺寸[28]、高材料刚度[29-31]等,对于低频(频率100 Hz 以下)且微振动(加速度10−6量级)应用场景的减振俘能一体化研究尚不充分.
驻极体是一种表面植入了永久电荷的智能材料,可使附近导体产生感应电荷.改变导体的相对位置,可引起导体内感应电荷量的变化,进而在导线中形成电流,实现驻极体振动能量回收(electret Vibration Energy Harvesting,eVEH)[32].由于eVEH 非接触、不依靠材料变形等优点,不受材料本身刚度、强度等影响,在制备能量回收装置时更加灵活、限制更少,更适用于微振环境.此外,eVEH 还具有输出电压高、成本低等优势,成为微振动俘能领域研究热点.Westby 等[33]利用驻极体开发了置于轮胎内的振动能量回收装置,以较小的体积可以实现车辆胎压监测.Perez 等[34]开发了一种风能回收装置,利用风致振动,在30 m/s 风速时能量收集功率为2.1 mW.Yang 等[35]综合利用驻极体材料和永磁体在15 Hz的振动激励下,获得了300 V 的开路电压.目前,对于驻极体的振动俘能研究,大多从提高俘能效率的角度出发,对其减振效果关注不够.这种单纯的追求俘能的做法,往往存在破坏原结构动平衡的可能,会给振动结构带来破坏性的影响.
本文将从兼顾减振和俘能的目标出发,设计一种驻极体减振俘能装置,利用驻极体换能器的静电力抵消主结构振动的影响,并将振动能量转化成电能.在传统的线性动力减振器设计理论基础上,融入驻极体俘能器的机电耦合模型,建立驻极体减振俘能装置的本构模型.在此基础上,本文采用能量方法给出静电力的等效动力学参数,从而分析静电力对系统动力学特性、减振、俘能效率的影响.基于所构建的动力学模型,对驻极体减振俘能装置的主要参数进行量化分析,并提出一种兼顾减振和俘能效率的双目标优化方法.采用AMESim 和Simulink 联合仿真环境,对理论分析结果进行验证.本文的工作将为低频微振动条件下的减振和俘能技术融合发展提供参考,为拓展驻极体换能器的工程应用提供新的思路.
1 结构设计和工作原理
本文所设计的驻极体减振俘能装置如图1 所示,其结构中包括主结构、动力减振器及安装于主结构和动力减振器之间的驻极体换能器.上下支架紧固于主结构,随主结构一起运动,下极板与驻极体固定于下支架.上支架包含4 个旋转对称的“L”形弹性梁,作为装置的弹性和阻尼元件.上极板固定于上支架中心,当“L”梁形变时,上极板与下极板产生相对位移.
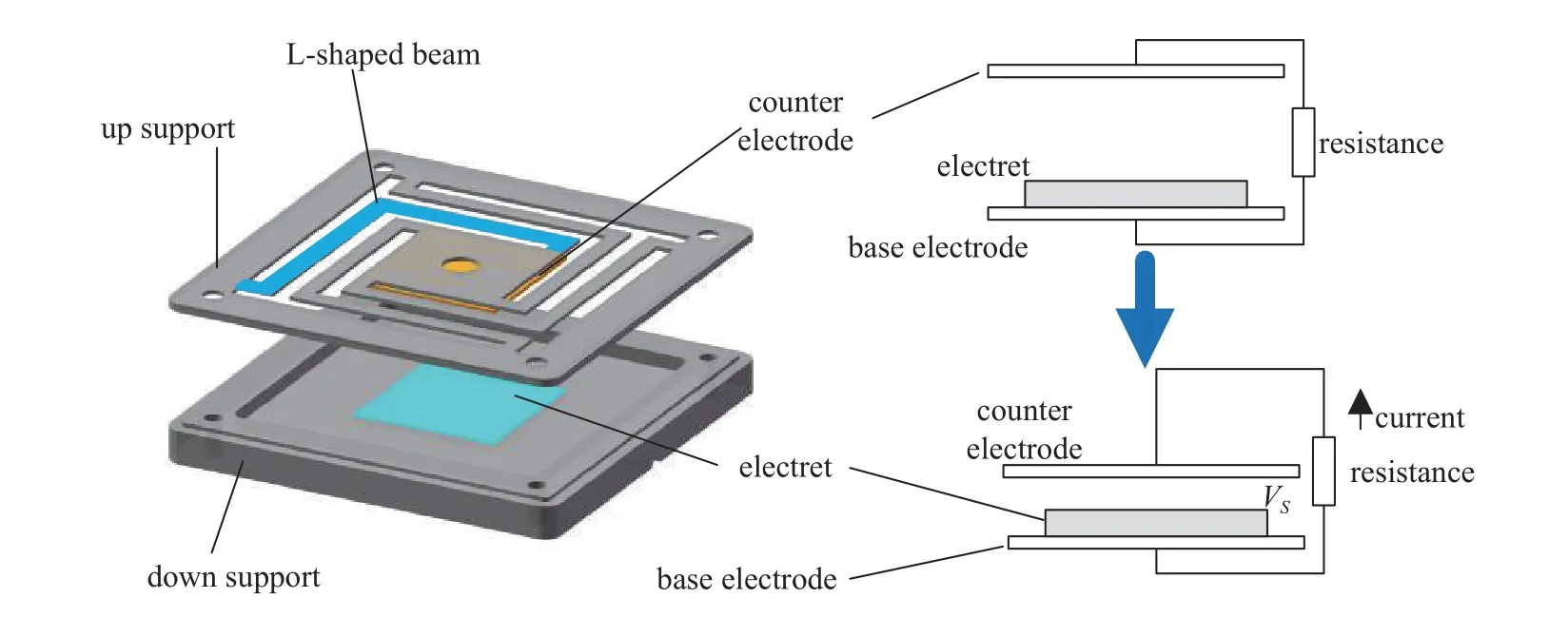
图1 驻极体减振俘能装置Fig.1 Electret vibration suppression energy harvesting device
在此结构中,上下支架、驻极体和下极板均固定于主结构,作为主结构的一部分,选用轻质材料,与主结构质量相差很大,几乎不对主结构位移产生影响.上极板与固定它的上极板中心(也可在其上附加质量块),作为副结构的质量块.当支架随主结构振动时,“L”梁产生弹性形变.未引入驻极体时,支架、极板构成了经典的动力减振器.引入驻极体后,驻极体既作为俘能部分,将机械能转化为电能,又由于静电力的作用对动力减振器造成影响,改变装置的运动状态.
系统的减振作用基于动力减振器理论: 动力减振器是一个两自由度振动系统,副结构(质量为m2)通过弹性元件(刚度为k2)和阻尼元件(阻尼为c2)附着于主结构(质量为m1)上,主副结构的固有频率接近.当主结构受交变力作用时,副结构吸收了主结构的部分振动能量,其运动为主结构提供了一个抵消运动的作用力,减弱了主结构的振动.在本装置中,支架及下极板固定于主结构上,上极板及其附加质量可视为副结构,由于小尺寸器件中不便于设置阻尼器,故阻尼由材料和结构阻尼实现,将“L”梁视为弹性和阻尼元件.
系统的俘能作用来源于驻极体换能器的机电转换原理: 驻极体换能器的基本结构包含驻极体薄膜、固定极板和移动极板.固定极板附着于驻极体薄膜底部,移动极板位于驻极体薄膜水平上方,并保持一定间隙.固定和移动电极之间通过导线连接.驻极体的表面植入电荷,可在固定极板和移动极板之间产生感应电场.改变移动极板与驻极体的间隙,可使极板上的电荷通过导线重新分布,从而形成电流、将机械能转化为电能.
2 模型的构建、仿真及参数优化方法
2.1 模型的构建
2.1.1 驻极体减振俘能装置机械模型
驻极体减振俘能装置受力如图2 所示,建立以主副结构运动方向为坐标轴方向的坐标系,以主结构质心静平衡位置为坐标原点.
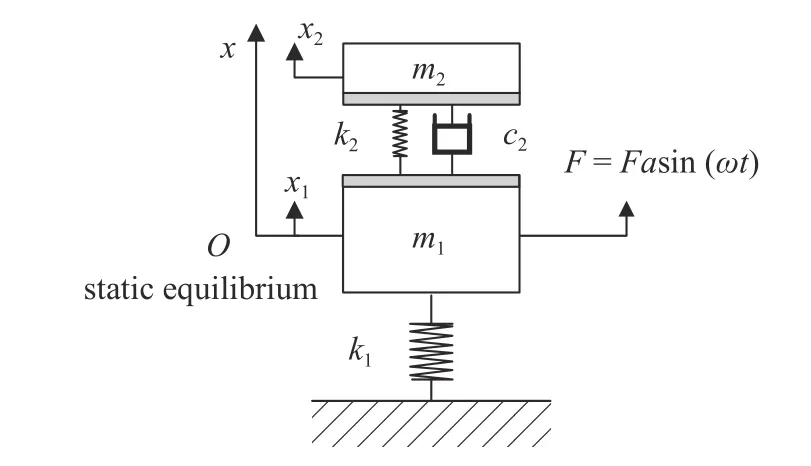
图2 驻极体减振俘能装置受力图(原点位于m1 静平衡位置)Fig.2 Force analysis of electret vibration suppression and energy harvesting device (orientation was selected as the equilibrium position of the primary structure)
根据动力减振器理论,当主结构质量m1,刚度k1确定后,依据设计需求和实际情况,确定主副结构质量比μ,则对于动力减振器,其副结构质量m2,刚度k2的最佳值k0,阻尼c2的最佳值c0分别为[36]
副结构的刚度k2由上支架中被切割出的4 个“L”形弹性梁提供,当支架随主结构振动时,“L”梁产生弹性形变,“L”梁两端可认为是固支的.上支架相当于4 个“L”梁并联,其刚度可表示为[37]
式中,J,I和l分别为“L”梁的极惯性矩、截面矩和单臂长度,E,G分别为材料的弹性模量和剪切模量.
在系统未引入驻极体时,主副结构的振幅分别为
式中,ω为激振频率.
此时,系统为理想动力减振器,具备最佳的线性减振效果.为便于与本文设计的驻极体减振俘能装置进行参数比较,理想动力减振器副结构选用其刚度和阻尼的最佳值,分别为k0和c0,其表达式参见式(1),而驻极体减振俘能装置的副结构刚度和阻尼则分别记为k2和c2.
2.1.2 驻极体减振俘能装置俘能模型
驻极体俘能模型的等效电路如图3 所示,图中VS为驻极体表面电势,Ce为极板等效的可变间距平行板电容,Cp为寄生电容,R为负载电阻,VL为负载电压.驻极体俘能装置的电容Ce为
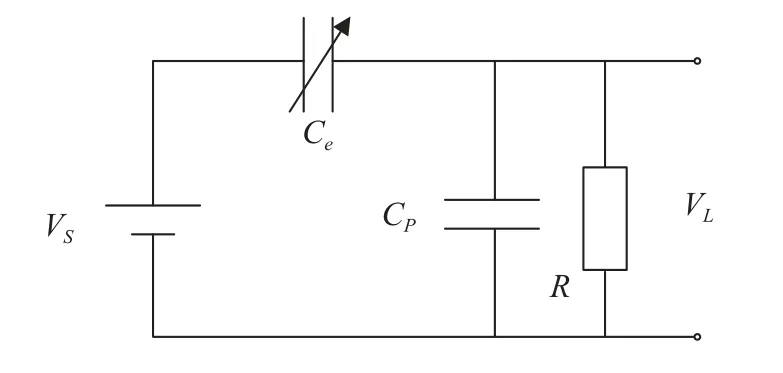
图3 驻极体俘能等效电路图Fig.3 The equivalent circuit of electret-based VEH
式中,A为极板面积,x为两极板间距的变化量,h0为初始空气间隙,h1为驻极体厚度,ε0和εr分别为空气和驻极体相对介电系数.
对于驻极体减振俘能装置,在主、副结构之间无碰撞的情况下,考虑寄生电容Cp,其机电耦合方程可表示为[32]
式中,R为负载电阻,Q为极板上的电荷量,Vs为驻极体的表面电压.负载电阻上的电压VL为
2.1.3 静电力的建模及等效
其中,Fc可进一步化简为
式中,U和I分别为极板构成的平行板电容器的充放电电压和电流(即干路电流),当不考虑寄生电容时,U=VS−VL.φc为与相关的非线性函数.
由式(9)可知,Fc是一个与x无关,只与相关的函数,可认为是由静电力引起的广义非线性阻尼力.
将Fk化简为
式中,φk为与x相关的非线性函数.由此可知,Fk是一个与无关,只与x有关的函数,可认为是由静电力引起的广义非线性弹性力.
综上,静电力Fe可以等效为广义非线性阻尼力和弹性力的共同作用,即
式(11)展示了静电力的弹性和阻尼分量的组成和变量关系,可以描述静电力的变化规律.但其与传统动力减振器的参数形式不一致,不便于建立统一的动力学模型,无法更为直接地表示静电力对传统动力减振器刚度、阻尼等参数设计的影响.因此,需要将式(11)进一步处理为等效参数的形式,从而统一动力学解析模型中的参数形式,利于建立一个更简洁的二阶振动方程组.此外,等效参数模型可以更直观展示静电力的动力学特性,有助于理解静电力中不同分量的变化趋势,便于定量分析驻极体减振俘能装置中静电力的影响.
首先将静电力中的弹性分量等效为非线性弹性力,其等效刚度为
从式(9)可知,静电力中的阻尼力分量具有明显的非线性.尤其是当主副结构的相对速度趋近于0 时,非线性阻尼力Fc在数值上趋于无穷,导致整个数值求解方法的不稳定.然而,这种概念中的无穷大阻尼力对系统的动力学特性并无明显影响,因为仅在某个时刻静电力的值无穷,且下个时刻反向无穷.在这个极短的时间邻域内,相互作用力变化极快,主副结构的能量不会突变,但难以准确描述.
因此,本文采用了一种能量平均方法求解等效阻尼系数.在一个振动周期内,电阻上消耗的能量为
式中,t0为初始时刻,T为一个振动周期,PL为俘能功率,VL为负载电阻上的电压.
从能量角度来说,弹性力是保守力,阻尼力是非保守力,即弹性力只在系统内转换能量,而阻尼力消耗系统能量.对于驻极体俘能装置,极板振动过程中引起的电荷分布,带来了两方面的影响,一是造成电容器中存储的静电能的变化,二是导致电荷在导线中流动,形成电流,继而在负载电阻上消耗电能.而电容器作为一个储能元件,本身不消耗能量.因此,阻尼力引起的能量损耗可理解为电路中负载电阻消耗的电能,静电力的等效非线性阻尼可以通过电阻上所消耗的功率表示,即
式中,Am为极板振幅.
需要说明的是,采用式(14)计算的等效阻尼并不能完全准确表示Fe中的阻尼系数.因为ce本质上是在每个振动周期内计算一个平均的阻尼值,不可避免地掩盖了静电阻尼的部分非线性.
2.1.4 驻极体减振俘能装置机电耦合模型
引入静电力的等效参数ke和ce后,联立式(5)、式(6)、式(12)和式(14),可得驻极体减振俘能装置的耦合机电方程.其状态变量为
式(15)可运用龙格库塔方法进行求解.由于阻尼部分采用了等效线性方法计算,模型中存在一定误差.但是式(15)的优势在于可以在全频带上较完整地体现阻尼力的变化规律,有助于初步设计驻极体减振俘能装置.
如不考虑驻极体的影响,系统可退化为传统的动力减振器系统.因此,在驻极体产生的静电力量级较小时,系统仍可依托经典的线性动力减振器理论进行初步设计,其相关参数设置仍可依据式(1)初步确定.
2.2 仿真验证方法
本文采用Simulink 与AMEsim 联合仿真环境对系统的减振、俘能特性进行仿真,并将其结果与理论模型的数值积分结果进行比对,从而验证理论模型的准确性.理论模型及数值仿真过程所采用的参数见表1.
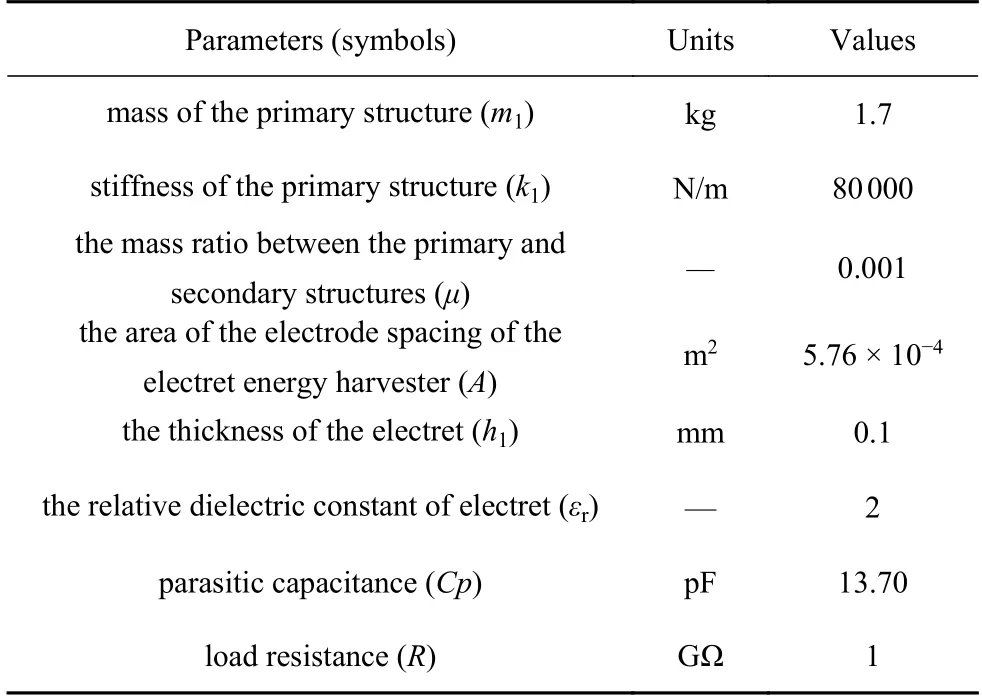
表1 驻极体减振俘能装置参数设置Table 1 Parameters of electret vibration suppression and energy harvesting device
在AMEsim 和Simulink 的联合仿真环境中构建的驻极体减振俘能装置仿真模型,由AMEsim 软件进行机械运动部分的仿真,如图4 所示,由Simulink软件进行静电力部分的仿真,如图5 所示.
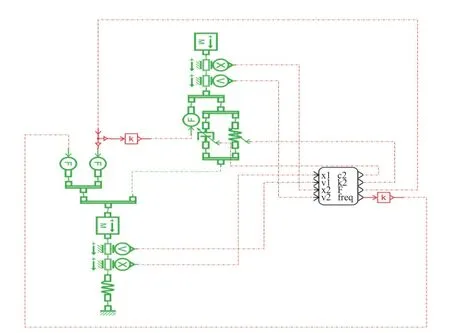
图4 AMEsim 机械模型仿真部分Fig.4 Mechanical field simulation in AMEsim
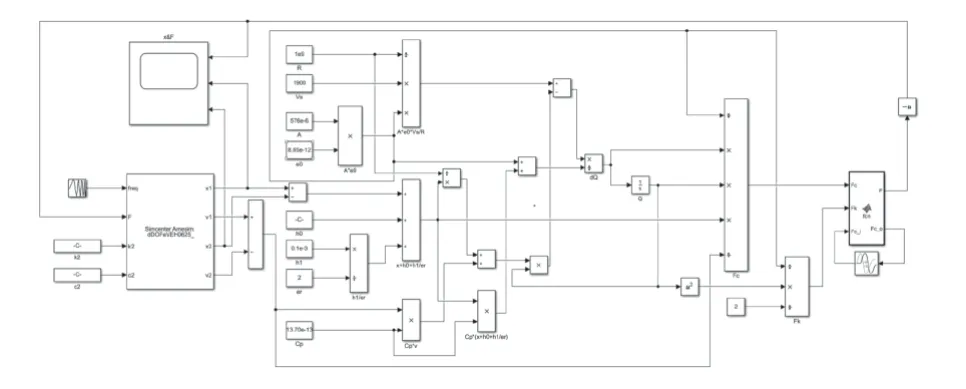
图5 Simulink 静电场模型仿真部分Fig.5 Electrostatic field simulation in Simulink
2.3 参数优化方法
传统的动力减振器设计理论已不能完全适用于驻极体减振俘能装置的设计,其原因如下: 首先动力减振器对动力学参数变化极为敏感,基于动力减振器设计理论所确定的最优质量、刚度、阻尼等参数一旦被静电力引入的等效刚度和等效阻尼所偏离,系统的减振性能就会大幅下降;其次传统动力减振器不具备俘能功能,相应的设计理论也无法平衡系统减振与俘能两方面的设计指标.
因此,本文针对驻极体减振俘能装置的设计需求,提出一种综合优化的方法,一方面能够补偿驻极体静电力对减振器最优刚度、阻尼等参数的偏离,另一方面能够平衡系统减振、俘能的双重设计指标.
为定量分析减振效果和俘能功率,寻求最优的参数设定,在确保主副结构不发生碰撞的前提下,权衡减振和俘能两个方面指标,构建的目标函数如下
式中,σx是无量纲化的减振效果减幅系数,σp是无量纲化的俘能功率增幅系数,a和b分别为权重系数,用以设定减振和俘能分别所占权重,a+b=1.
由式(3),可以得到理想动力减振器的主副结构振幅,则驻极体减振俘能装置两极板间距初始设定为
式中,η为尺寸参数,取值略大于1,一般可取1.2.
在理想动力减振器中,B1和B2规定了主副结构能达到的最大位移,只要初始间距大于B1与B2之和,主副结构就不会发生“碰撞”或者“吸合”.在驻极体减振俘能装置中,由于静电力的非线性作用,主副结构的位移会大于B1和B2,但无法用准确的解析式表达,为避免主副结构“碰撞”或“吸合”,适当放大理想动力减振器的初始间距用于驻极体减振俘能装置.
至此,驻极体减振俘能装置的全部初始参数均已确定,可根据此参数计算初始主结构振幅max(x1(k2))和初始俘能功率P0.无量纲化的俘能功率增幅系数为
无量纲化的减振效果减幅系数为
式(16)中h0是优化的参数之一,式(17)中hs的初值不影响最终优化的结果,只影响优化计算的速度.式(19)中的分母为未引入驻极体时理想动力减振器主结构的最大振幅,与主副结构的间距无关.
3 结果分析
3.1 仿真结果验证
采用表1 的参数设置,分别计算理论和仿真结果如图6 所示.
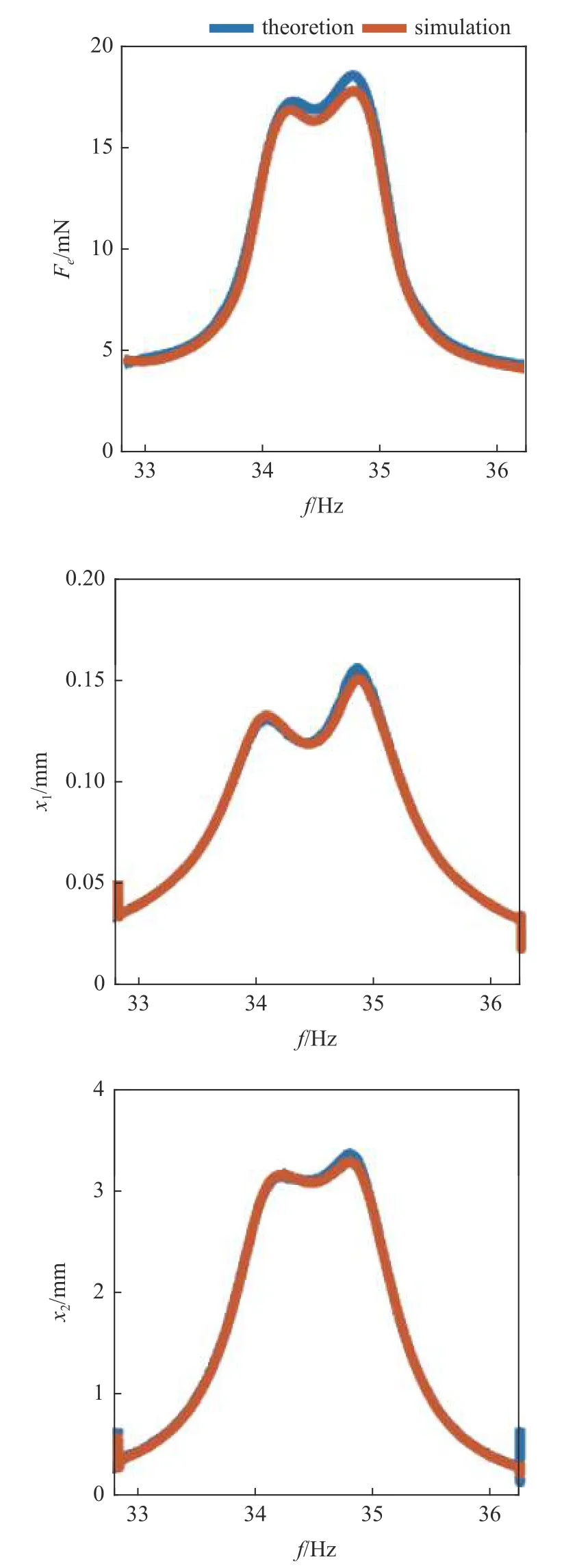
图6 理论计算和仿真结果对比Fig.6 Comparison of theoretical calculation and simulation results
由图6 可知,理论计算结果与仿真分析结果十分接近,主副结构振幅的误差均控制在5%以内,静电力曲线波形重合度很好,且变化趋势相同,说明了机电耦合模型准确预测了静电力的变化趋势和主副结构的振动形态.
3.2 减振、俘能效率分析
3.2.1 动力减振器结构参数分析
为研究不同的结构设计参数对系统减振效率的影响,对减振器刚度k2,阻尼c2进行了参数扫掠,其结果如图7 所示.为进一步体现位移对参数变化的敏感性,对k2和c2和主结构最大振幅进行了归一化处理,即: 分别采用k2/k0和c2/c0作为系统的横、纵坐标,采用不同颜色表示主结构在其固有频率± 3 Hz 邻域内,最大振幅相对于理想动力减振器最大振幅的比值.
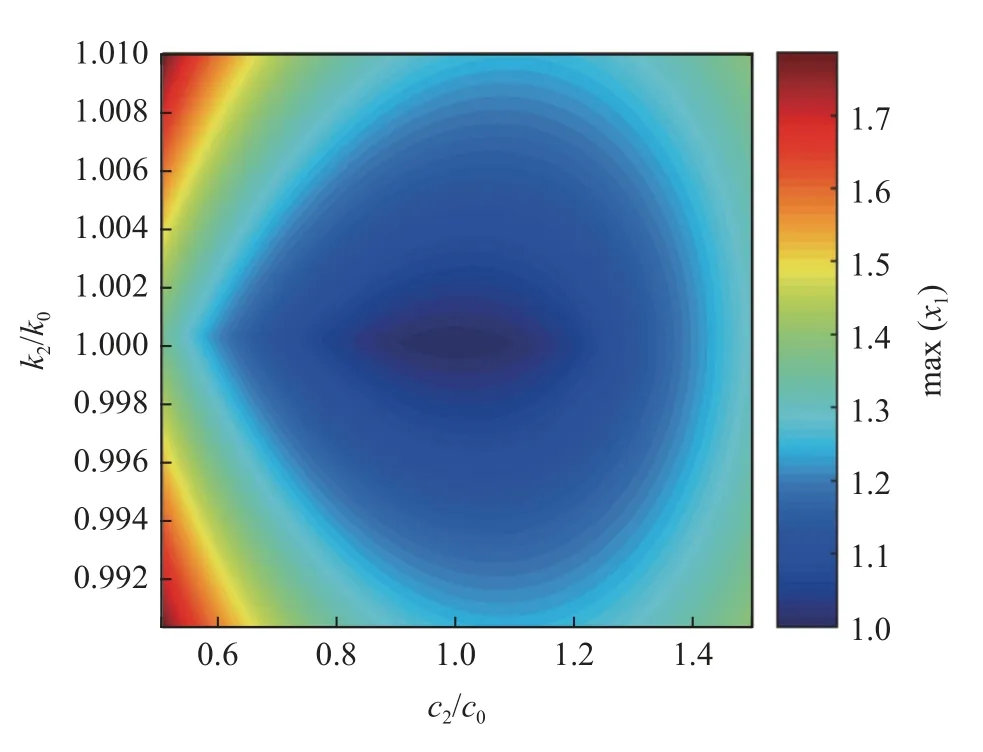
图7 副结构刚度和阻尼对主结构最大振幅的影响Fig.7 Influence of the stiffness and damping of the secondary structure on the maximum amplitude of the primary structure
由图7 可知,在低频、小质量比工况下,副结构刚度k2对减振效果的影响要显著大于阻尼c2.副结构刚度相对于其理想刚度k0的微小变化,即可引起主结构振幅的剧烈增加,副结构的刚度变化约0.5%,即使得主结构振幅增大了近20%.而副结构阻尼对主结构影响则要相对较弱,副结构阻尼的变化值要接近20%时,才能使主结构振幅增大20%.
此外,副结构的初始刚度k2对主结构的振幅影响十分明显,对k2的扫频结果如图8 所示.由动力减振器的设计理论,当副结构的刚度小于设计值时,主结构高频共振幅值将大于低频,反之则低频大于高频.且副结构刚度偏离越远,两共振峰相差越大.在驻极体减振俘能装置中,由于静电力的强非线性影响,副结构刚度在理论值附近变化1 N/m,使主结构最大振幅由0.14 mm 增大至0.17~ 0.19 mm.
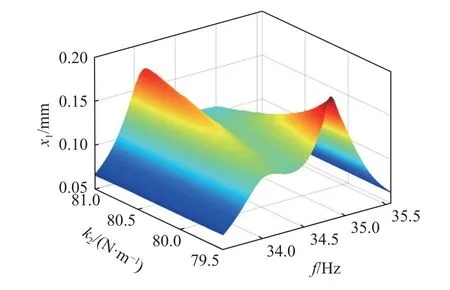
图8 副结构刚度对主结构幅频响应的影响Fig.8 Influence of the stiffness of the secondary structure on the amplitude-frequency response of the primary structure
3.2.2 驻极体初始间距分析
当主副结构的参数与理想动力减振器相同时,不同极板间距下,主结构的幅频曲线如图9 所示.
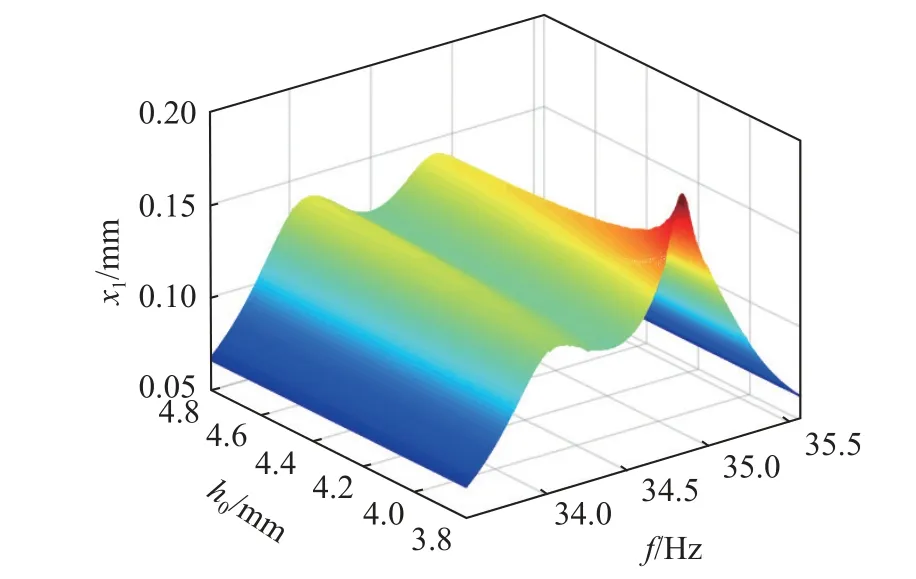
图9 极板间距对主结构幅频响应的影响Fig.9 Influence of electrode spacing on the amplitude-frequency response of primary structure
极板间距的改变不会影响传统动力减振器幅频特性,而驻极体减振俘能装置的幅频特性随极板间距的变化,是由于极板间的静电力造成的.由图9 可知,在驻极体减振俘能装置中,静电力的作用效果与动力减振器中副结构刚度小于设计值的现象一致.两极板间距越小,静电力的作用越明显.当两极板的间距大于5 mm 时,主结构的振幅曲线接近于理想动力减振器,在固有频率附近,有两个幅值相等的共振峰.此时静电力对结构振型的影响很微弱,驻极体减振俘能装置的减振效果近似于理想动力减振器.当两极板的间距小于4 mm 时,静电力的作用显著,使主结构的振幅出现了较大变化,两个共振峰的幅值不再相等,其中高频振幅明显增大,最大振幅超过0.19 mm.在驻极体减振俘能装置中,当极板间距变小时,静电力增大,使主结构的共振峰向高频部分移动.
极板间距对驻极体减振俘能装置俘能功率的影响与其对幅频曲线的影响基本相同,如图10 所示,随着极板间距的缩小,装置的俘能功率逐步由不足1 mW 提升至接近3 mW,曲线的对称性不断下降.一是由于极板间距的缩小,相同表面电势的驻极体可以在极板上吸引出更多电荷;二是由于静电力的影响,极板间距的缩小导致装置主副结构振幅增大,幅频曲线改变,也导致了俘能功率升高和对称性下降.
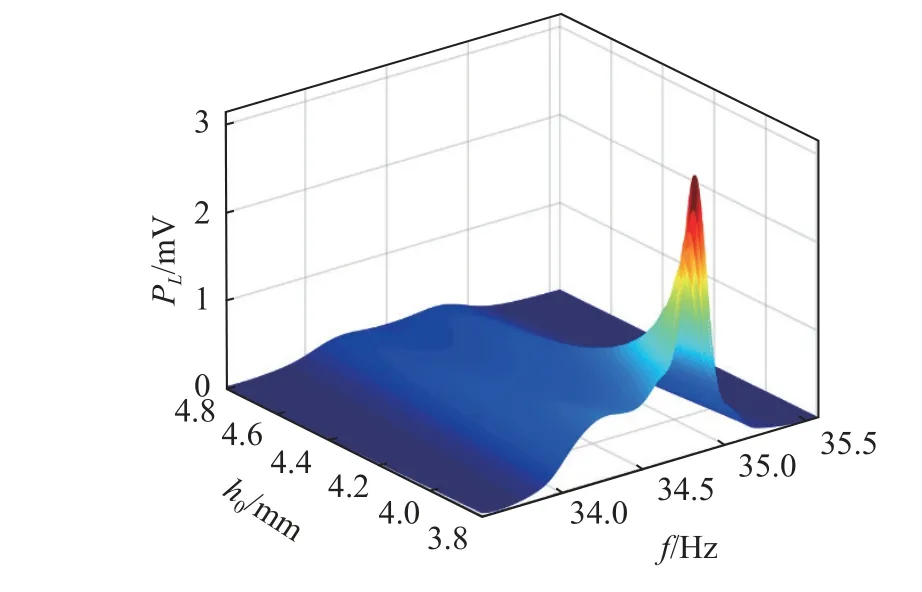
图10 极板间距对俘能功率的影响Fig.10 Influence of electrode spacing on energy harvesting
综合比较极板间距h0和副结构刚度k2对减振效果和俘能功率的影响,结果如图11 所示,图中颜色图分别表示该参数设定下主结构的最大位移和最大瞬时功率.
对比图11(a)和图10(b)可知,主结构振幅和俘能功率相较于极板间距h0和副结构刚度k2的变化趋势并不相同.对于主结构振幅而言,存在明确的位移最小值以达到最佳的减振效果,即图11(a)中曲面的凹槽处.但是俘能功率随着极板间距减小和副结构刚度的改变而急剧增大,曲面不存在极大值点.因此,图11 反映了减振效果和俘能功率相较于参数的变化情况,但由于两者相对于参数的变化趋势并不相同,无法在理论上给出一个兼顾减振和俘能的最优参数.而且由于缺乏统一的度量指标,理论建模只能分别对减振和俘能进行定量分析,其综合性能依然只能定性描述,因此必须依据式(16)进行综合参数优化.
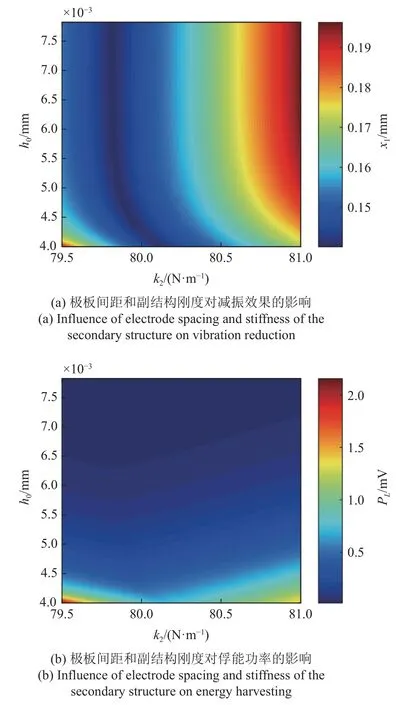
图11 极板间距和副结构刚度对减振效果和俘能功率的影响Fig.11 Influence of electrode spacing and stiffness of the secondary structure on vibration suppression and energy harvesting
3.3 参数优化结果验证
3.3.1 仅考虑减振目标的参数优化
为验证驻极体减振俘能装置的减振能力,定义优化算例1 和对照算例1 和2 如下.
优化算例1:a=1,b=0;用于计算驻极体减振俘能装置在专注减振时的工作状态.
对照算例1: 理想动力减振器,即严格采用式(1)计算所得的参数设置,系统中不引入驻极体换能器,不考虑静电力影响.该算例的目的是为了验证优化算法在退化成仅考虑减振情况下的结果准确性,对比理想动力减振器与驻极体减振俘能器的减振能力.
对照算例2: 未优化的驻极体减振俘能装置,即参数设置与理想动力减振器保持一致,引入驻极体,考虑静电力对装置的影响.该算例用于量化计算驻极体减振俘能装置性能在优化后提升的程度.
使用MATLAB 软件优化工具包中的fmincon函数进行寻优,优化前后参数见表2.
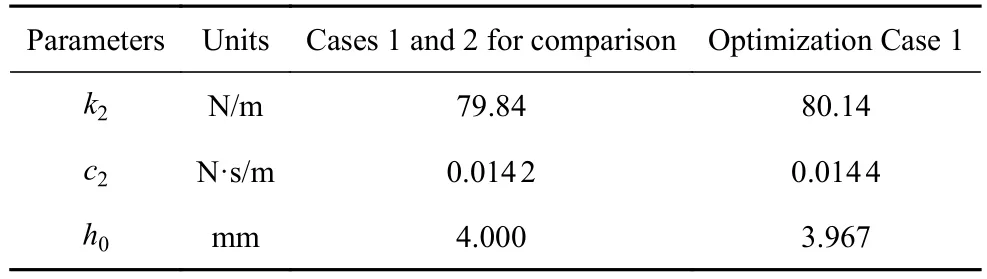
表2 仅考虑减振目标的参数优化结果(优化算例1)及对照算例1 和2 的参数选取Table 2 Parameter optimization results considering only vibration suppression (optimization Case 1) and the parameters of Cases 1 and 2 for comparison
优化算例1、对照算例1 和2 的减振与俘能效果如图12 所示,红色、绿色、黄色曲线分别表示理想动力减振器(对照算例1)、未优化的驻极体减振俘能装置(对照算例2)和专注减振(a=1,b=0)的驻极体减振俘能装置(优化算例1),图12(a)~图12(d)依次为主结构振幅、副结构振幅、输出电压和俘能功率.
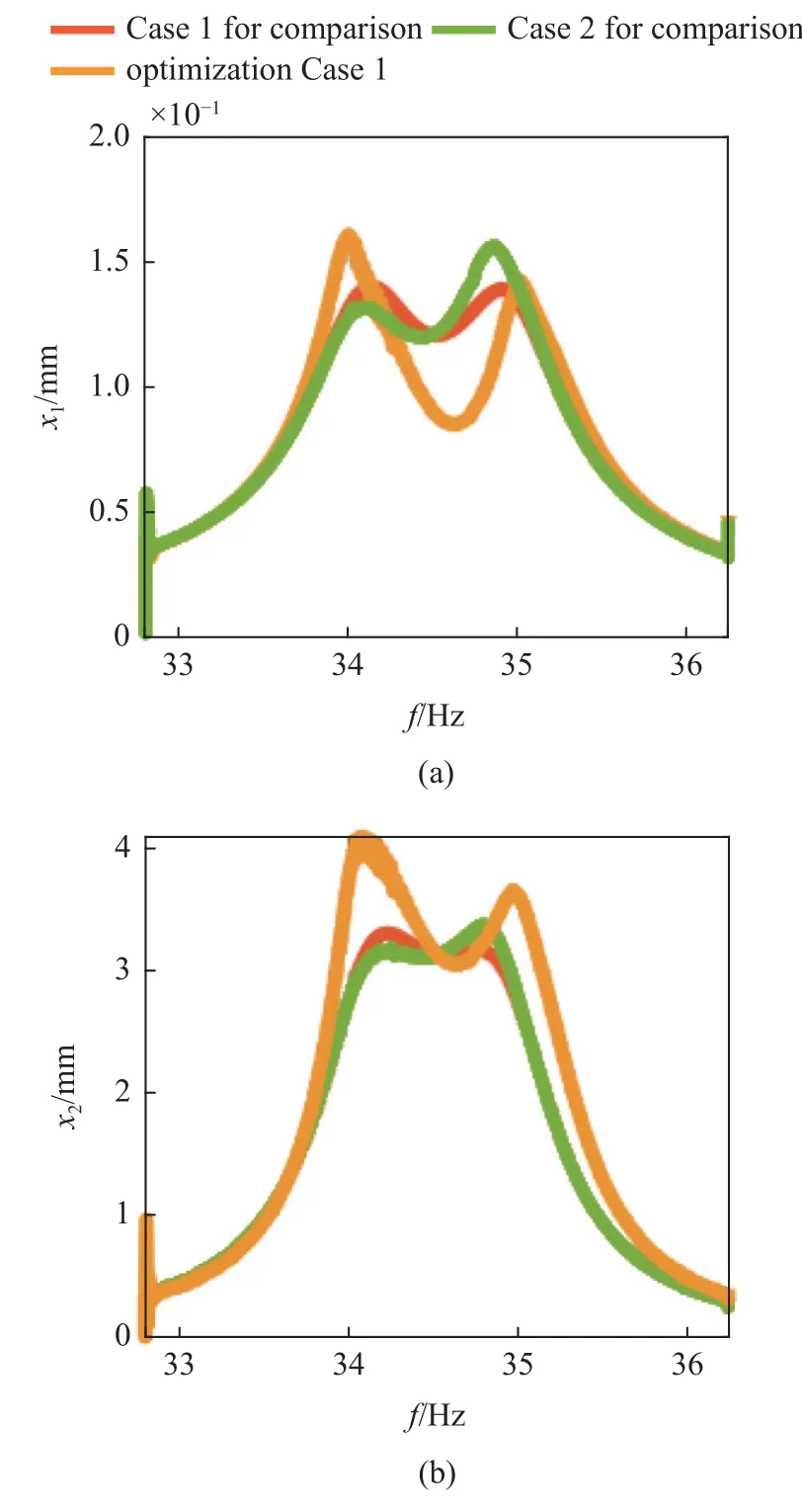
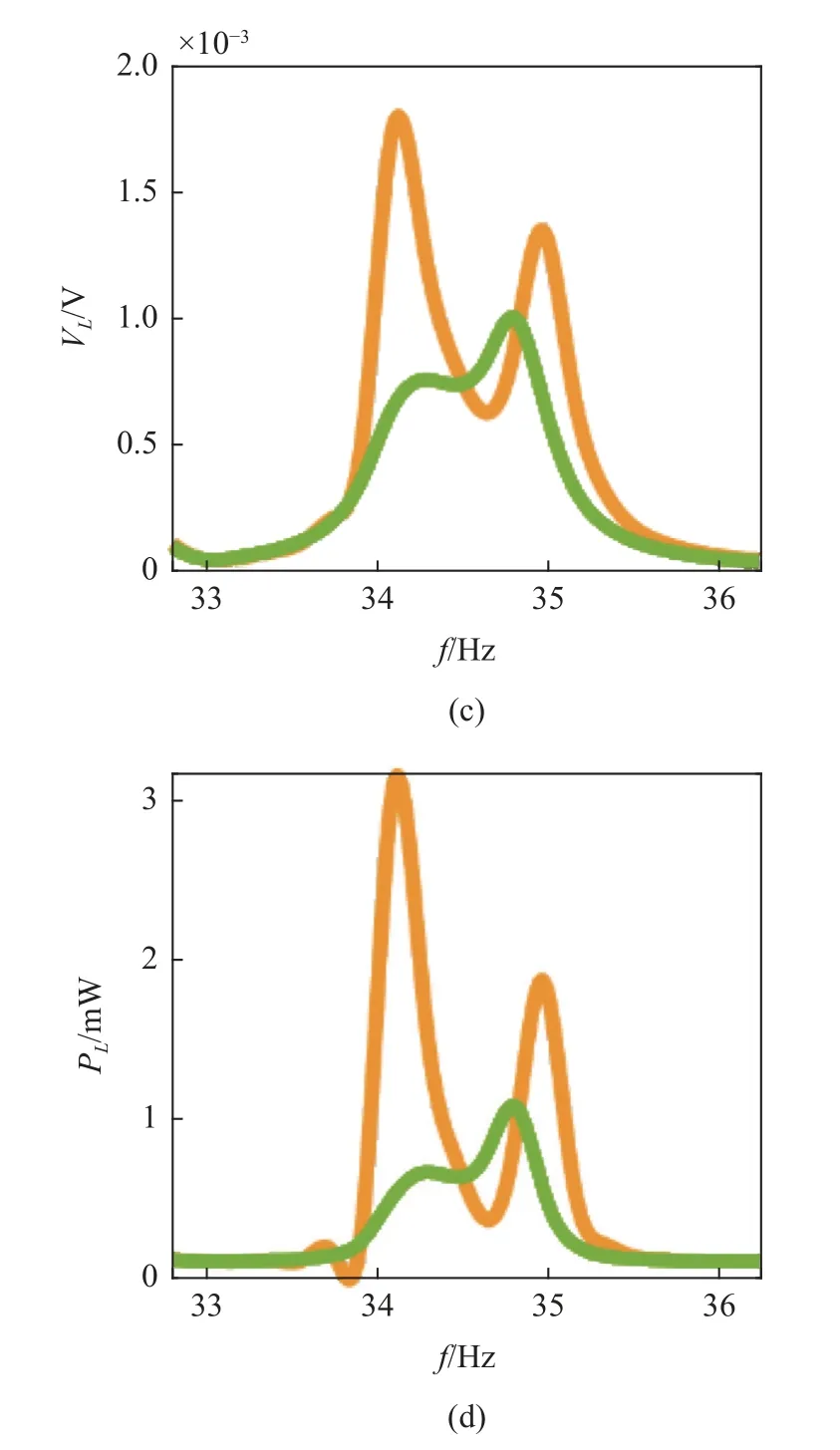
图12 优化算例1 及对照算例1 和2 的幅频特性及俘能特性对比Fig.12 Comparison of amplitude-frequency response and energy harvesting of optimization Case 1 and Cases 1,2 for comparison
由图12 可知,在1.5×10−7g的激励力下,未经优化时,采用相同参数的驻极体减振俘能装置的减振能力弱于理想动力减振器,其主结构最大振幅为0.16 mm,比理想动力减振器高14.3%.经过优化,在完全放弃提升俘能功率的前提下,驻极体减振俘能装置的减振性能与理想动力减振器基本一致,优化算例1 与对照算例1 的主结构幅频曲线近乎重合,以至于图11 中的红色曲线不明显,最大位移控制在0.14 mm 左右.此时优化算例1 输出电压依然可达800 V,俘能功率接近0.7 mW.证明了本文提出的设计思路合理,设计的驻极体减振俘能装置具有不弱于传统动力减振器的综合性能,经过合理设计,在保证减振效果的同时,依然具有较好的能量回收能力.
3.3.2 综合考虑减振和俘能目标的参数优化
为验证驻极体减振俘能装置能够兼顾减振俘能两方面性能要求,定义优化算例2 和对照算例3 如下.
优化算例2:a=0.8,b=0.2;该算例用于综合考虑减振俘能两种需求,验证其在损失部分减振能力时能达到的较为优良的俘能功率.
对照算例3: 对优化算例2 中优化后的副结构刚度k2增大0.1%,极板间距h2增大10%,再进行仿真计算,用于验证参数确能通过优化方法兼顾减振俘能两方面需求,稍微偏离最优参数则使其性能受到很大影响;
需要说明的是,本文设置的减振权重a总是高于俘能权重b,这是由于驻极体减振俘能装置的设计中,减振性能的优先级要高于俘能效率.当俘能权重设计过高时,主副结构在运动过程中距离会过近,此时静电力的吸合作用明显,导致主副结构出现碰撞甚至吸合.此时,驻极体减振俘能装置丧失减振能力,不在本文的讨论范围内,为避免出现上述情况,减振权重设置高于俘能权重.
使用MATLAB 软件优化工具包中的“fmincon”函数进行寻优,优化前后参数见表3.
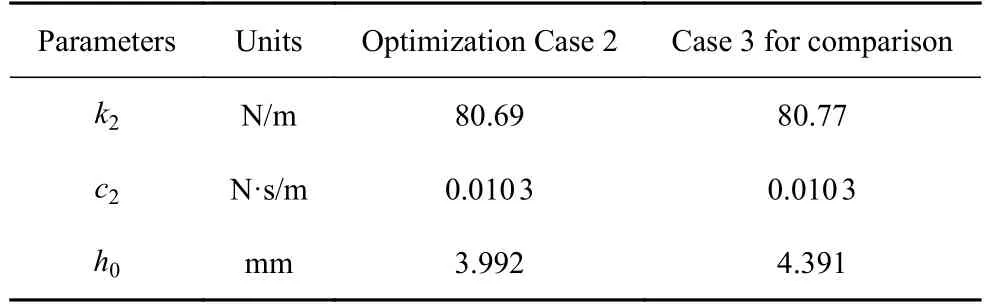
表3 同时考虑减振与俘能的参数优化结果(优化算例2)及对照算例3 的参数选取Table 3 Parameter optimization results considering both vibration suppression and energy harvesting (optimization Case 2) and the parameters of Case 3 for comparison
其减振俘能效果如图13 所示.
由图13 可知,在优化后,主结构最大振幅降至0.16 mm,减振能力较理想动力减振器降低15%.优化后的俘能电压由1200 V 增加至1700 V,增幅约41.7%,最大瞬时俘能功率由1.2 mW 增加至3.1 mW,增幅约141.7%.图13 说明,驻极体减振俘能装置类似于理想动力减振器,虽然减振效果较理想动力减振器有所下降,但依然能够有效抑制主结构的谐振振幅.驻极体减振俘能装置优化后,减振性能有所提升,但是由于非线性静电力的影响,和兼顾俘能功率的需求,其减振性能依然弱于理想动力减振器.优化后,在低频弱激励条件下,驻极体减振俘能装置的俘能电压和功率均有明显提升,分别达到了41.7%和141.7%,证明了提出的优化策略的有效性,验证了本文提出的思路和结构能够有效兼顾减振和俘能需求.
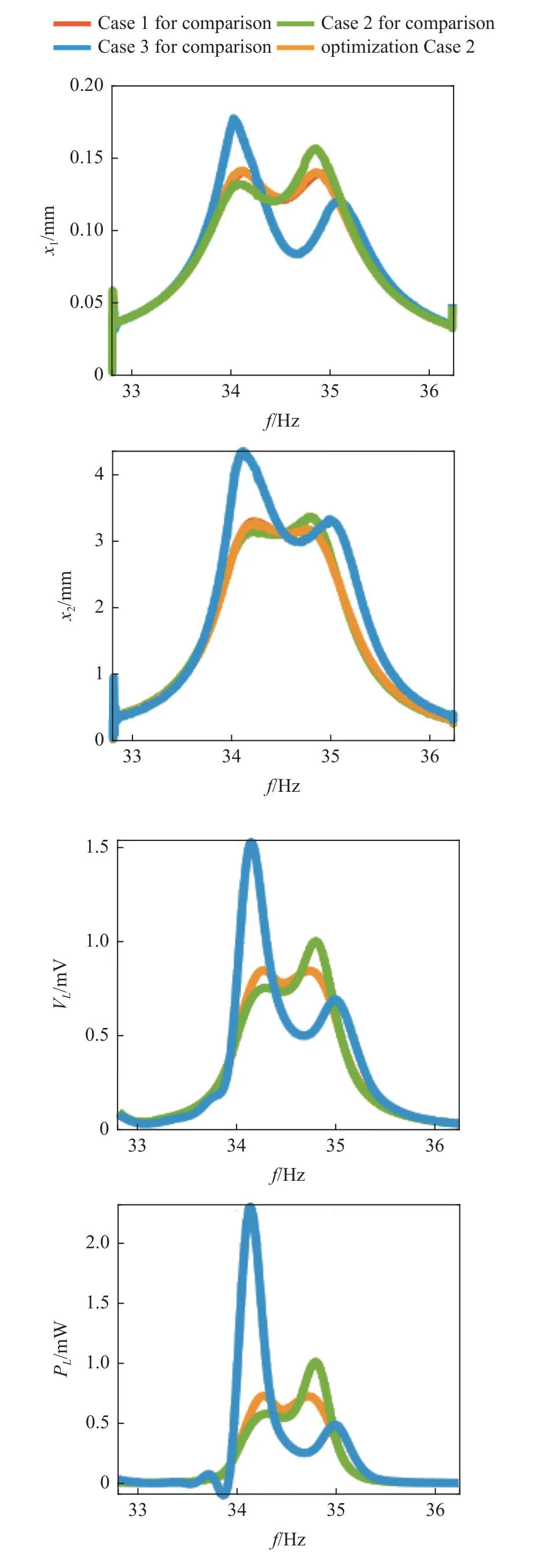
图13 优化算例2 及对照算例1,2,3 的幅频特性及俘能特性对比Fig.13 Comparison of amplitude-frequency response and energy harvesting of optimization Case 2 and Cases 1,2,3 for comparison
优化算例2 与优化算例3 关键参数相差很小,但是其减振效果与俘能功率均出现减弱.主结构最大振幅由0.16 mm 增大至0.18 mm,增幅达12.5%,相对于理想动力减振器,增幅达38.5%.驻极体减振俘能装置的最大瞬时俘能功率由2.9 mW 降低至2.3 mW,降幅为20.7%.说明了驻极体减振俘能装置对参数变化十分敏感,微小的参数差异即可引起其性能改变.本文提出的优化设计方法能够准确计算驻极体减振俘能装置的最佳参数,满足兼顾减振和俘能的设计需求.
4 结论
本文设计了一种基于驻极体的减振俘能装置,并建立了其机电耦合模型,分析了非线性静电力的动态等效参数,进行了参数分析和优化,计算了理论减振效果和俘能效率,完成了联合环境仿真验真,可以得到如下结论.
(1)本文所设计的驻极体减振俘能装置满足预期效果,兼顾了微振动减振和俘能两个方面的需求,当设计目标专注于减振性能时,副结构刚度为80.1 N/m,极板间距为3.97 mm 时,减振效果接近传统线性动力减振器.通过调整参数,在牺牲15%减振效果的前提下,副结构刚度调整为80.7 N/m,极板间距为3.99 mm 时,最高可获得1700 V 的输出电压和3.1 mW 的输出功率.
(2)本文建立的驻极体减振俘能装置机电耦合模型可以准确描述其运动过程,与仿真模型误差控制在5%以内,曲线波形重合度很好.
(3)驻极体减振俘能装置副结构刚度和极板间距对减振和俘能性能影响很大,副结构刚度在理论值附近变化1 N/m,使主结构最大振幅由0.14 mm增大至0.17~ 0.19 mm.极板间距小于4 mm 时,主结构的振幅两个共振峰的幅值不再相等,其中高频振幅明显增大,最大振幅超过0.19 mm.
(4)驻极体减振俘能装置对参数变化十分敏感,相较于最优参数,当副结构刚度增大0.1%,极板间距增大10%时,主结构最大振幅增大12.5%,最大瞬时俘能功率降低20.7%.

