垂向双蝠鲼变攻角滑翔水动力性能研究1)
高鹏骋 刘冠杉 黄桥高 ,2) 潘 光 马云龙
* (西北工业大学航海学院,西安 710072)
† (中国船舶集团有限公司系统工程研究院,北京 100094)
引言
鱼类集群运动的现象随处可见,集群游动能帮助鱼群中各个体有效规避捕食者,提升捕食效率,增加繁殖机会等[1-3].此外,许多学者认为鱼类可以通过高度组织化的群体运动来保存能量,获得水动力优势,提高个体的运动性能.
大多数研究认为,鱼群游动的水动力优势是由于涡流假说和槽道效应[4].其中,涡流假说认为,鱼群中后鱼置身于前鱼的尾涡中,通过传入的尾涡结构的诱导速度降低了鱼和水流间的相对速度,后鱼同时还能借助前鱼尾涡提高游动效率.槽道效应指出,通过增加相邻鱼之间在游泳方向的水流速度来降低鱼和水流间的相对速度,同时鱼类还可以借助相邻鱼涡街诱导出的流动来提高游动效率.
近年来,随着计算方法以及数值仿真软件的发展,学者们对鱼群水动力性能进行了大量仿真计算,并得到了许多有意义的结论.Deng 等[5]采用改进的浸入边界法对菱形鱼群中的3 条鱼单元进行了数值模拟.结果表明,位于前一列两条鱼之间的后鱼可以利用上游鱼脱落的反卡门涡街来提高推进效率以及降低功耗.随后,Chung[6]在文献[5]的基础上进行了深入研究,给定了3 条鱼最优的位置及运动参数设置,即两条前鱼横向间距为0.4 倍弦长,进行反相波动运动,后鱼的前缘距前鱼后缘0.2 倍弦长.Tian 等[7]通过有限元法数值求解不可压缩的Navier-Stokes 方程来研究子母鱼对的游泳性能和涡结构,计算结果表明母鱼和小鱼在串联和交错排列中都受益,通过改变它们的相位差和相速度,可增加推力和降低功耗.目前,还有不少学者利用强化学习算法来对先导-跟随群游结构中的跟随鱼进行运动控制,其中先导鱼的运动方式固定,跟随鱼通过强化学习来调整运动方式,以实现跟随鱼利用先导鱼的涡流来提升推进效率[8-9].
王亮[10]对二维仿真鱼群游动进行了数值模拟,指出当鱼群中各个体存在体形差异时主要利用侧向水动力(即槽道效应)来提高推进效率;当个体体形相近时,主要利用前鱼尾涡提高效率.Li 等[11]对串联、并联、菱形和矩形4 种编队的鱼群游动进行了数值模拟.结果表明,效率受到尾流和侧向压力的影响,其中尾流主要影响推力,横向功率损失受到侧向压力影响.Lin 等[12-15]对二维鳗式游动鱼群开展了系列研究,探究了相位差、间距对串联鱼群及倾斜布置鱼群的水动力性能影响.
随着电机驱动技术,传感器技术以及流场显示技术的发展,一些学者开始设计搭建实验装置来研究鱼群游动的节能机理[16-21].Dewey 等[16-17]与Boschitsch 等[18]分别实验研究了两个柔性扑翼在并联与串联布置时的水动力性能,并利用DPIV 系统进行流场记录及显示.实验结果表明,对于并联结构,两个翼形的推进特性相同: 同相拍动时,效率提升而推力减小(相对于单个翼形);反相拍动时,推力增加而效率基本不变.对于串联结构,前翼的推力和效率在分离距离较大时与单个翼形一致,而后翼由于受到前翼尾流的影响,其动力学特性与分离距离和相位差相关.
当前国内外关于集群水动力特性研究广泛集中于二维翼型而非三维生物的研究.并且,研究主要集中在二维平面的群游,而没有考虑到集群中各单体沿垂向分布的情况,然而通过Vicsek 等[22]的研究表明生物在实际游动过程中往往采取上下错落分布队形.此外,目前的研究对象大多为尾鳍摆动推进鱼群,忽略了对采用滑扑结合推进的鳐科生物的研究.
蝠鲼属鳐科生物,有着扁平形的身体、较大的展弦比,巡游速度在0.25~0.47 m/s[23].蝠鲼采用扑动与滑翔相结合的推进方式[24],效率可高达89%,高于鳗科、鲹科等水中生物[25-27],在机动性、隐蔽性等方面具有超凡的优越性.为弥补现有研究的不足以及探究双蝠鲼垂向间距和攻角(α)对各个蝠鲼水动力性能的影响,本文针对沿垂向分布的双蝠鲼进行滑翔运动时的水动力特性开展研究,其中垂向间距选取了0.25TL(TL为体厚),0.5TL,0.75TL,1TL4 种工况,在每种工况下进行了攻角变换,变化范围为−8°~8°(每2°取一个特征攻角),以期为仿蝠鲼滑扑一体航行器在滑翔时的队形设置提供参考数据.
1 数值计算方法
1.1 仿真模型及计算域设置
采用逆向工程技术建立蝠鲼数值计算模型,通过测量实际物体的尺寸,获得物体的三维点数据,再通过点数据构建三维曲线,进一步构建三维曲面,进而重构实物的CAD 模型[28],如图1 所示.其中展长(SL)为2900 mm,体长(BL)为1800 mm,最大体厚为350 mm.

图1 蝠鲼模型Fig.1 Manta ray model
我们将4 种间距排布统一展示在图2 中,计算域尺寸根据实际排布方式进行适应性调整,其中保证入口与蝠鲼间距4 倍体长,出口与蝠鲼间距7 倍体长,展向壁面距蝠鲼3 倍展长,上、下壁面分别距上下蝠鲼3 倍体厚.边界条件设置如下: 入口边界设为速度入口,出口边界设为压力出口,壁面设为自由滑移壁面,蝠鲼表面设为静止无滑移壁面.
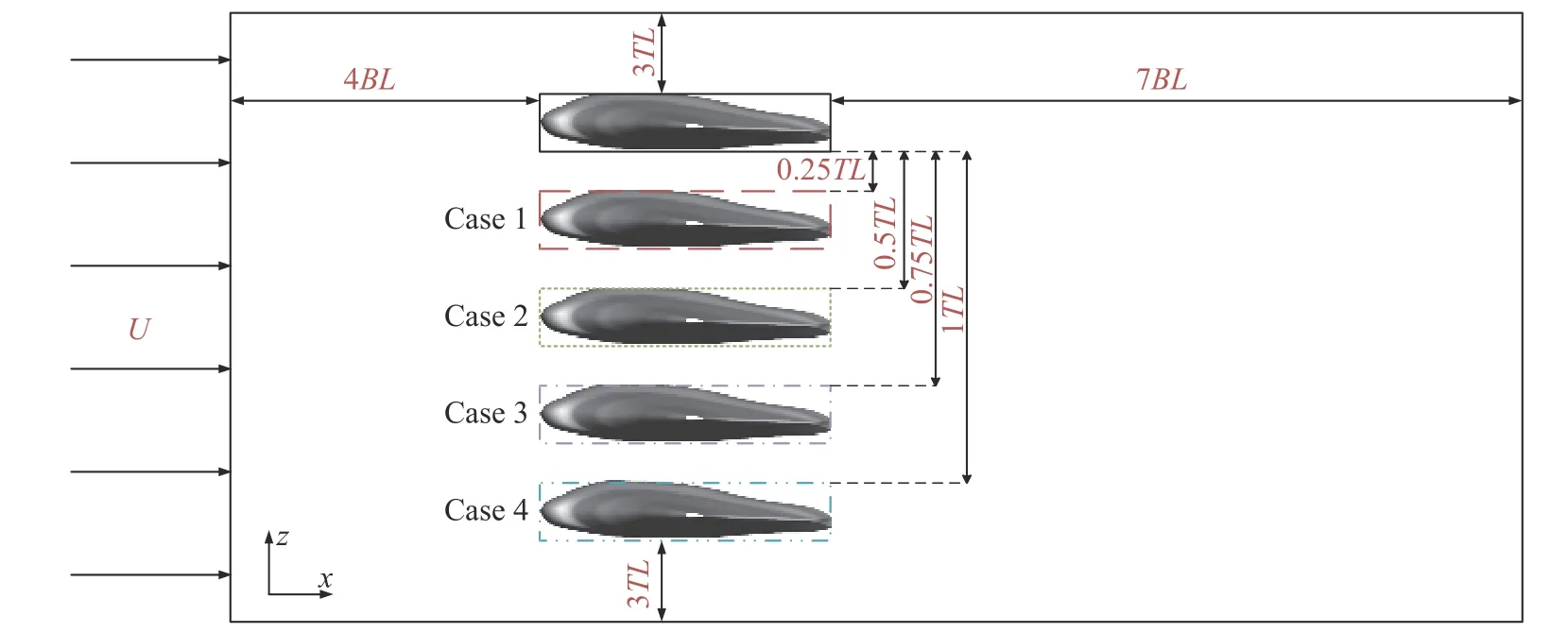
图2 计算域设置Fig.2 Calculation domain setting
本文在4 组垂向间距(0.25TL~1TL)以及9 组攻角(−8°~8°)组合下进行了仿真计算,探究了集群滑翔时,垂向间距和攻角对集群中各单体和集群系统的水动力特性的影响.
1.2 水动力参数定义
根据文献[29],双体蝠鲼滑翔状态下的系统平均阻力(Ddouble)按照下式计算
其中,Dup和Ddown分别代表了上、下蝠鲼所受到的阻力.
将蝠鲼集群滑翔过程中的受力无量纲化
其中,D,L为蝠鲼所受的阻力、升力,ρ为流体密度,U为来流速度,BL为蝠鲼体长.
2 网格无关性验证与数值验证
2.1 网格无关性验证
本文借助ICEM 进行结构网格绘制,由疏到密绘制了4 套网格(网格数量分别为1.5 × 106,3 × 106,4.5 × 106,6 × 106)进行单体仿真计算,以期确定出在保证计算精度前提下兼顾计算速度的网格节点设置(如图3(a)所示).图3(b)展示了在4 套网格下,蝠鲼单体在0°攻角下以0.5 m/s 速度滑翔的阻力系数(CD)、升力系数(CL)数值仿真结果.可以看出当单体网格设置为4.5 × 106时,计算结果精确度已经达到最优,为节省计算成本,提高计算速度,在后续的双体蝠鲼仿真计算中我们沿用了此时的节点设置.

图3 网格细节及无关性验证Fig.3 Grid detail and independence verification
2.2 数值计算方法验证
本文借助 FLUENT 软件进行计算,湍流模型设置为SSTk-ω模型,采用 SIMPLEC 算法对连续方程中的压力和速度的耦合,收敛残差设置为1.0 × 10−5.
采用此方法对三维渐变NACA0009 翼型在雷诺数Re=1.0 × 106时不同攻角下的阻力系数(CD)、升力系数(CL)进行了仿真计算,并与文献[30]的实验数据进行比对,如图4 所示.由图4 可知: 数值仿真所得到的CD和CL与实验值接近,确保了数值计算方法的可靠性.
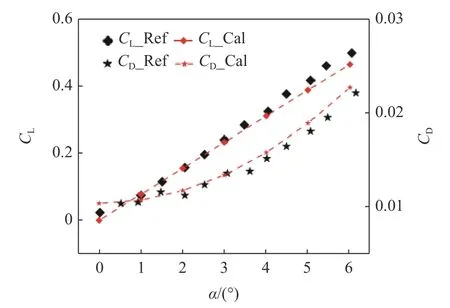
图4 方法验证Fig.4 Method validation
3 数值计算结果与分析
本节展示了双蝠鲼以0.5 m/s 速度滑翔时,不同垂向间距下阻力(升力)系数随攻角的变化情况.研究发现,间距和攻角对各阻力系数产生较大影响,但对升力系数,尤其是系统平均升力系数影响较小.因此,本节按照垂向间距划分小节,在每小节中结合压力云图对各阻力系数进行分析,在垂向间距为0.25TL时结合蝠鲼表面压力云图探究升力系数变化.
3.1 垂向间距0.25TL
本小节对垂向间距0.25TL的双蝠鲼集群滑翔进行了数值模拟,集群中各单体攻角保持同步变化,变化范围为−8°~8°.图5 展示了上(下)方蝠鲼阻力(升力)系数、双蝠鲼系统平均阻力(升力)系数以及单体蝠鲼阻力(升力)系数随攻角变化的改变情况.由图5(a)可以看出,系统平均阻力均大于单体滑翔时所受到的阻力.但当双蝠鲼以负攻角滑翔时,下方蝠鲼受到阻力远低于单体滑翔,尤其是在−8°攻角时,几乎不受到阻力;当以正攻角滑翔时,上方蝠鲼受到的阻力减小,下方蝠鲼受到阻力增加.与此同时,我们还发现当攻角为−2°时,上下两蝠鲼受到的阻力几乎相同.由图5(b)可以看出,当滑翔攻角小于−2°时,系统平均升力大于单体滑翔时的升力;当滑翔攻角大于−2°时,系统平均升力小于单体滑翔时的升力;当滑翔攻角为−2°时,系统平均升力与单体滑翔升力接近.此外,我们还发现上方蝠鲼所受升力始终小于下方蝠鲼.
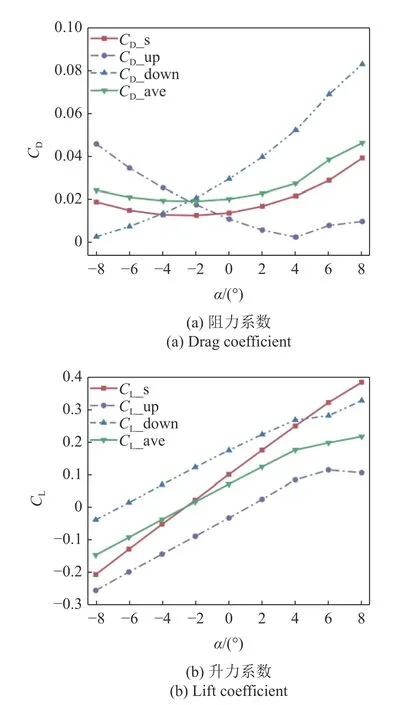
图5 0.25TL 垂向间距时不同攻角下的阻力/升力系数Fig.5 Drag/lift coefficient at different attack angles at 0.25TL vertical distance
为进一步探究阻力(升力)出现变化的原因,我们将压力/速度云图绘制在了图6 中,其中压力取值范围为−300~150 Pa,速度取值范围为0~0.8 m/s,后续所有云图中取值范围保持一致.从图6(a)和图6(b)可以看出,无论以何种攻角进行集群滑翔时,蝠鲼外围压力场分布相似,即在蝠鲼的头部及尾部附近各存在着一个高压区,高压区的面积及压力大小几乎一致.当蝠鲼集群以不同攻角集群滑翔时,集群中各单体出现阻力差异的原因在于各单体的表面压力出现变化.由图6(a)可以看出,下方蝠鲼头部的中下部分处于低压区,而上方蝠鲼头部完全处于高压区,这必然导致下方蝠鲼的阻力减小,上方蝠鲼的阻力增加.由图6(b)可以看出,当以正攻角进行集群滑翔时,上方蝠鲼头部的中上部分处于低压区,下方蝠鲼头部完全处于高压区,因此下方蝠鲼的阻力增加,上方蝠鲼的阻力减小.接下来,结合图6(c)解释上下两蝠鲼升力表现,从图6(c)中可以看出,上下两蝠鲼上表面压力分布基本相似,下方蝠鲼头部压力略高于上方蝠鲼;下方蝠鲼下表面压力明显高于上方蝠鲼,尤其是在蝠鲼的中腹部,上方蝠鲼存在着明显的低压区.又因为升力受表面压力影响较大,因此下方蝠鲼所受升力总是大于上方蝠鲼.由图6(d)可以看出两蝠鲼中间区域速度最高,尾部速度最低,头部存在小面积低速区,因此在蝠鲼尾部及头部出现高压区,在两蝠鲼中腹部周围出现低压区,这和压力云图相契合.通过结果统计,我们发现双蝠鲼沿垂向分布集群滑翔时各升力系数几乎不受间距和攻角的影响,在后续小节中为避免重复,仅结合压力云图对阻力表现进行分析.与此同时,我们发现随着间距的增加,集群滑翔对速度场影响逐步减弱,我们后续仅在间距为1TL时展示速度云图.

图6 0.25TL 垂向间距时不同攻角下的压力/速度云图Fig.6 Pressure/velocity diagram at different attack angles at 0.25TL vertical distance
3.2 垂向间距0.5TL
同3.1 节,图7 展示了当垂向间距为0.5TL时,上(下)方蝠鲼阻力(升力)系数、系统平均阻力(升力)系数以及单体蝠鲼阻力(升力)系数随攻角变化的改变情况.由图7(a)可以看出,系统平均阻力仍大于单体滑翔时所受到的阻力,但相较于0.25TL间距时,有所下降.上(下) 方蝠鲼的阻力变化趋势同0.25TL一致.由图7(b)可以看出,系统平均升力变化不大,上下两蝠鲼升力差值减小.
同样,我们将−8°,4°时的压力云图绘制在了图8 中,压力云图分布情况同间距为0.25TL时大致相同,从图8(a)可以看出,在以负攻角滑翔时,上方蝠鲼头部的中下部开始出现低压区,这将导致上方蝠鲼的阻力出现下降,这与图5 和图7 的阻力系数曲线图相符.当以正攻角滑翔时,上下蝠鲼的表面压力相较于间距为0.25TL时没有明显变化,因此在推力曲线上也几乎一致.
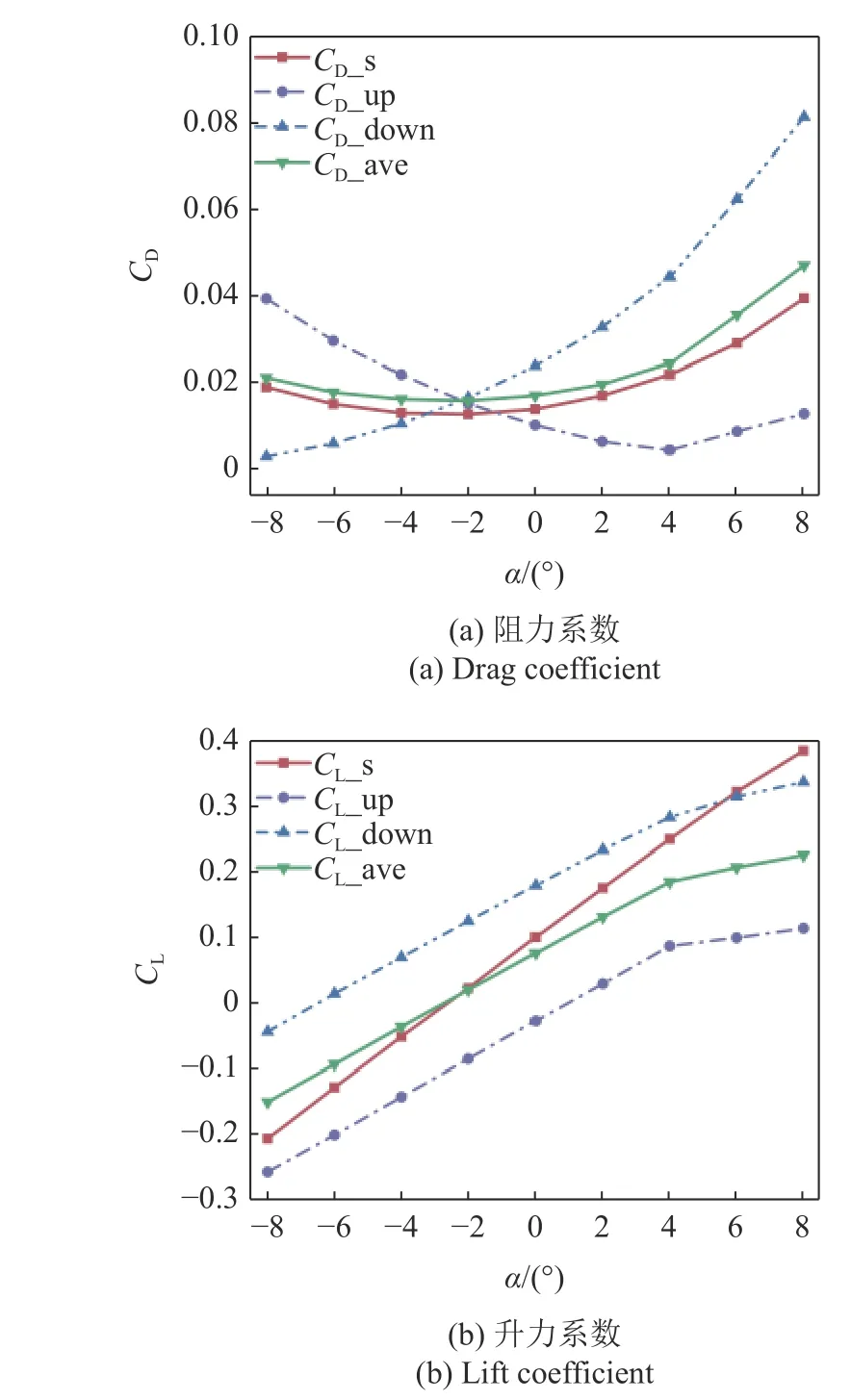
图7 0.5TL 垂向间距时不同攻角下的阻力/升力系数Fig.7 Drag/lift coefficient at different attack angles at 0.5TL vertical distance
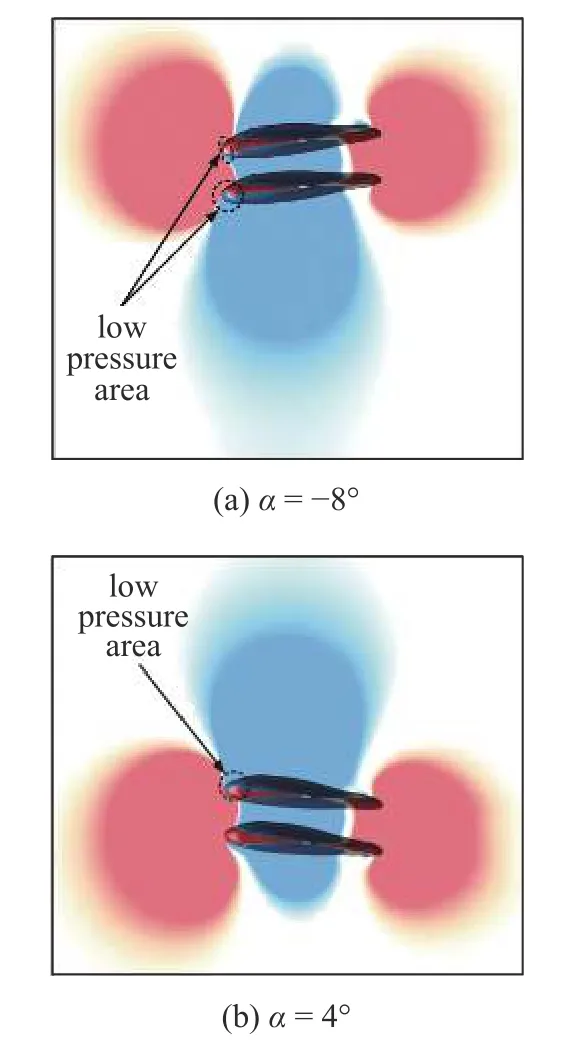
图8 0.5TL 垂向间距时不同攻角下的压力云图Fig.8 Pressure diagram at different attack angles at 0.5TL vertical distance
3.3 垂向间距0.75TL
同前,图9 展示了当垂向间距为0.75TL时,上(下) 方蝠鲼阻力(升力) 系数、系统平均阻力(升力)系数以及单体蝠鲼阻力(升力)系数随攻角变化的改变情况.由图9(a)可以看出,系统平均阻力更加接近单体滑翔时所受到的阻力,上、下方蝠鲼的阻力差值也减小,说明垂向间距的增大,集群中单体间相互影响降低.同样,我们将−8°,4°时的压力云图绘制在了图10 中,从图10(a)可以看出,在以负攻角滑翔时,上方蝠鲼头部的中下部低压区面积扩大,使得上方蝠鲼阻力进一步降低(见图9).从图10(b)可以发现以正攻角滑翔时,下方蝠鲼头部开始出现低压区,使得下方蝠鲼的阻力减小(见图9).由此可以看出,随着垂向距离的增加,集群中各单体间的相互作用减弱,系统平均阻力和单体滑翔阻力逐步接近.由图9(b)可以看出,系统平均升力变化不大,上下两蝠鲼升力差值进一步减小.
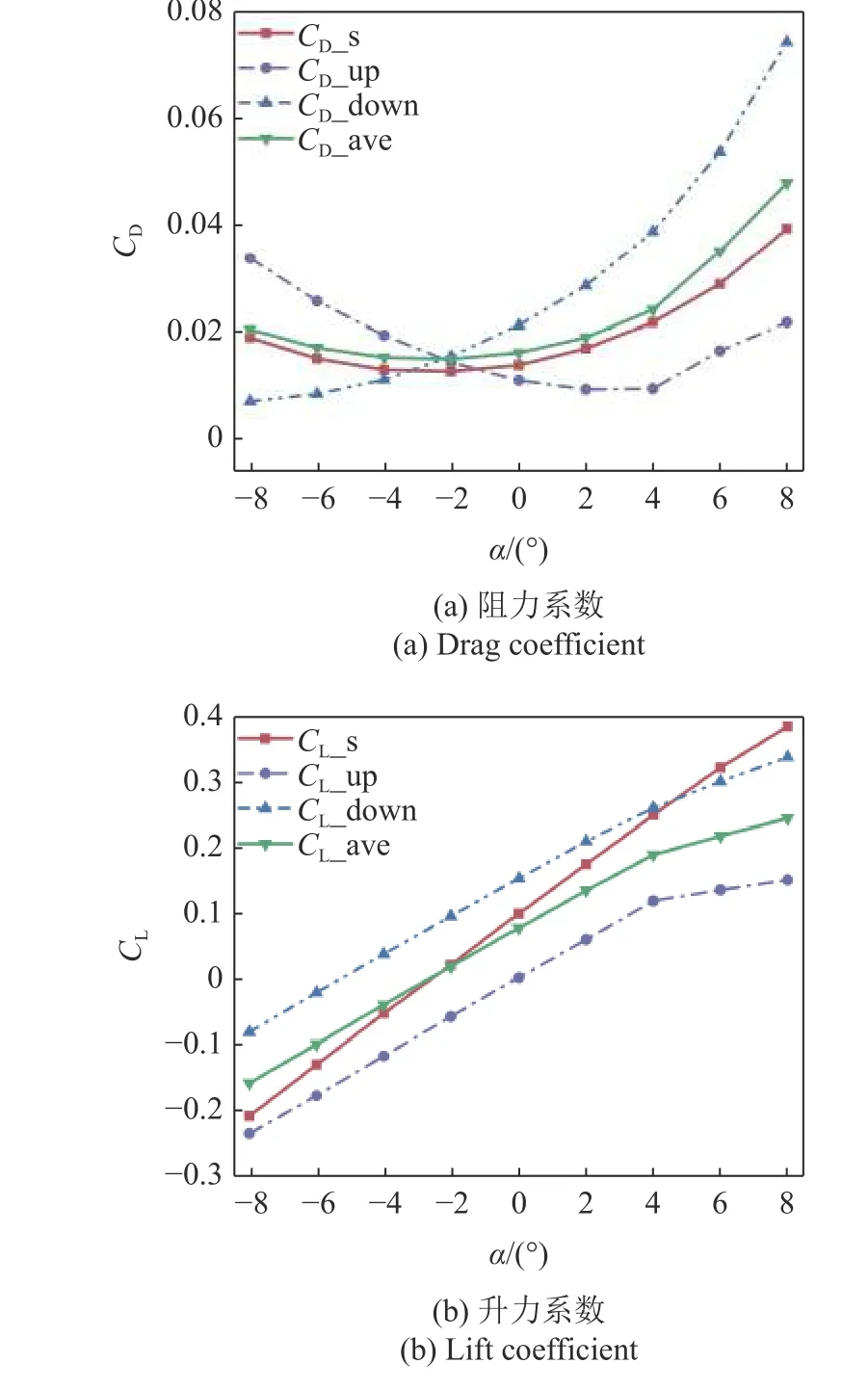
图9 0.75TL 垂向间距时不同攻角下的阻力/升力系数Fig.9 Drag/lift coefficient at different attack angles at 0.75TL vertical distance
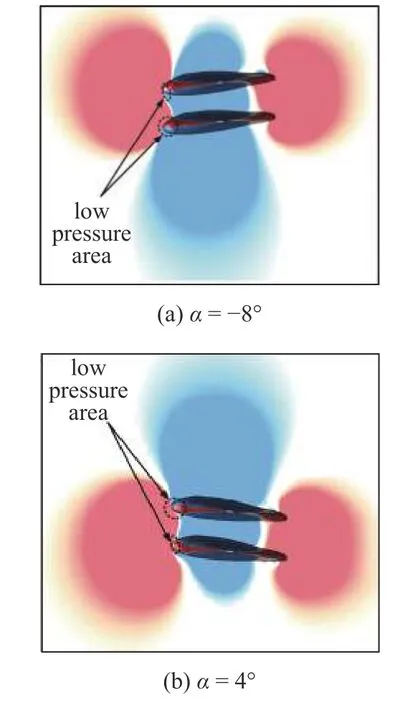
图10 0.75TL 垂向间距时不同攻角下的压力云图Fig.10 Pressure diagram at different attack angles at 0.75TL vertical distance
3.4 垂向间距1TL
同前,图11 展示了当垂向间距为1TL时,上(下)方蝠鲼阻力系数、系统平均阻力系数以及单体蝠鲼阻力系数随攻角变化的改变情况.由图11(a)可以看出,当攻角在−8°,−4°时,系统平均阻力与单体滑翔时所受到的阻力几乎保持一致,上、下方蝠鲼的阻力差值也进一步减小,集群中单体间相互影响进一步削弱.由图11(b)可以看出,系统平均升力变化不大,随着垂向距离的增加,上下两蝠鲼的升力差值也随之减小.我们将−8°,4°时的压力/速度云图绘制在了图12 中,从图12(a)和图12(b)可以看出,当以负攻角滑翔时,上方蝠鲼头部的中下部低压区面积扩大,使得上方蝠鲼阻力进一步降低,类似的,当以正攻角滑翔时,下方蝠鲼头部的低压区面积也有所增加,因此此时下方蝠鲼的阻力也随之减小.由图12(c)可以看出随着间距的增大,上下两蝠鲼的速度云图几乎保持一致,集群滑翔对集群中各单体的速度场影响减弱.
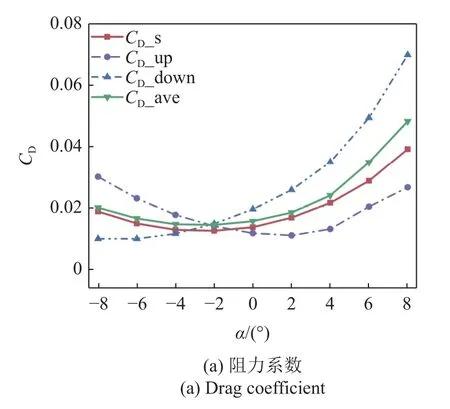
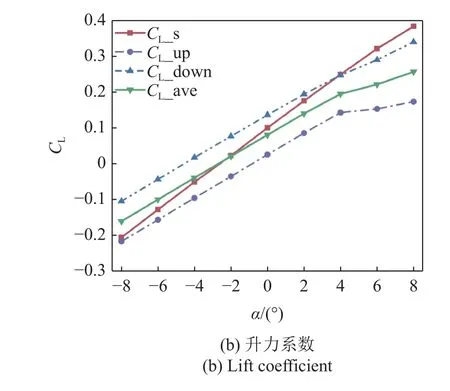
图11 1TL 垂向间距时不同攻角下的阻力/升力系数Fig.11 Drag/lift coefficient at different attack angles at 1TL vertical distance

图12 1TL 垂向间距时不同攻角下的压力/速度云图Fig.12 Pressure/velocity diagram at different attack angles at 1TL vertical distance
4 结论
本文借助Fluent 软件对沿垂向分布的双蝠鲼集群滑翔状态进行了数值仿真,得到了升力、阻力系数曲线,并结合压力云图进行分析,得到了如下结论.
(1)系统平均升力受垂向间距影响较小,当滑翔攻角小于−2°时,系统平均升力大于单体滑翔时的升力;当滑翔攻角大于−2°时,系统平均升力小于单体滑翔时的升力;当滑翔攻角为−2°时,系统平均升力与单体滑翔升力接近.下方蝠鲼升力总大于上方蝠鲼,但随着垂向间距增加,上下两蝠鲼升力差距减小.
(2)双蝠鲼沿垂向分布在攻角范围为−8°~8°进行集群滑翔时未能发现系统平均阻力低于单体滑翔时所受阻力的情况,但随着垂向间距的增加,单体间相互影响降低,系统平均阻力趋近于单体滑翔阻力.
(3)系统平均阻力虽未能发现减阻效果,但集群中单体能从集群滑翔中获得减阻收益.当双蝠鲼以负攻角集群滑翔时,下方蝠鲼获得减阻收益,且垂向间距越小,获得的减阻效果越明显;当以正攻角集群滑翔时,则是上方蝠鲼获得减阻收益.
(4) 双蝠鲼集群滑翔过程中各单体阻力(升力)表现的差异性主要来源于蝠鲼头部、中腹部压力区的变化,垂向间距的变化改变了压力区分布,从现有结果可以看出随着垂向间距的进一步加大,上(下)蝠鲼压力分布会趋于一致.

