涡波一体乘波飞行器宽速域气动优化设计研究1)
刘超宇 屈峰,2) 李杰奇 白俊强 刘传振 白 鹏 钱战森
* (西北工业大学航空学院,西安 710072)
† (中国运载火箭技术研究院,北京 100076)
** (中国航天空气动力技术研究院,北京 100074)
†† (中国航空工业空气动力研究院,沈阳 110034)
引言
近年来,具备宽速域、宽空域、水平起降等能力的空天飞行器成为研究的热点.此类飞行器要求从常规机场水平起飞,历经低速、跨声速、超声速直至高超声速巡航等多个飞行阶段[1],因此,如何在宽速域内保持良好的气动性能是此类飞行器研究的难点.常规的构型比如细长体、组合体、融合体、升力体等,高超声速气动性能欠佳[2].相应地,乘波飞行器利用前缘的附体激波阻止气流泄露,具有更好的高超声速升阻特性,已成为多款高超声速飞行器的基础构型[3].但是,传统的乘波体设计方法都是基于超声速假设建立的,通常具有低速气动性能不佳的缺陷.因此,若要将乘波理念应用于空天飞行器,如何提升其宽速域气动性能至关重要[4].
当前,国内外关于如何改善乘波体在低速时气动特性的研究相对较少,比较有代表性的是涡升力乘波体[5-7].其中,刘传振等[2,8-11]基于密切锥方法,通过对平面形状的合理定制引入涡效应,分别在高超声速和低速使用激波和旋涡提高气动性能,提出了一种涡波一体宽速域乘波飞行器.但是该类飞行器在设计过程中进行基准流场建立时忽略了三维效应、低速效应、以及黏性效应,因此其高低速气动特性均有较大的优化设计空间[2].此外,工程化的外形需要在理论模型的基础上实现头部/前缘钝化以及侧缘设计,而这些局部变化会对其气动特性产生较大的不利影响.因此,为使涡波一体宽速域飞行器更具工程应用价值,有必要对其开展兼顾不同速域性能的气动优化设计.
近年来,诸多学者针对飞行器兼顾不同速域气动性能的优化设计开展了研究.例如,Ueno 等[12]对高超声速翼型进行了优化设计,在保证高超声速高升阻比的同时,兼顾了翼型的跨声速气动性能.随后,Ueno 等[13]又采用梯度优化方法开展了机翼的宽速域气动优化设计研究,优化得到的二维翼型配置到机翼上可以明显改善机翼的宽速域气动性能.国内的孙祥程等[14]和张阳等[15-17]也开展了高超声速宽速域翼型优化设计研究,并得到了宽速域性能改善后的新翼型.但是,上述研究仍处于初步探索阶段,且多针对二维翼型或三维机翼等局部构件,缺乏三维复杂飞行器整机的宽速域优化设计研究.
气动优化设计方法方面,目前常用的气动优化设计方法主要可分为非梯度优化方法和梯度优化方法.非梯度优化方法主要包括启发式优化方法和代理优化方法,这些优化方法虽具有较强的全局寻优能力,但在针对设计变量众多的宽速域乘波飞行器三维整机开展气动优化设计时,会出现计算量过大的不足,一些情况下甚至可能得不到收敛结果[18-21].而基于伴随方程的梯度类优化设计方法可实现计算量与设计变量之间的基本解耦,并且精度较高,在大规模设计变量问题中具有明显优势[22],比较适合于设计变量众多的涡波一体宽速域飞行器整机气动优化设计.
综上所述,为了进一步改善涡波一体乘波飞行器的宽速域气动特性,本文采用一种基于离散伴随的宽速域飞行器气动优化设计方法,针对涡波一体乘波飞行器开展了兼顾高低速域气动性能的三维整机气动优化设计研究,以期为宽速域大空域的空天飞行器设计提供参考.
1 涡波一体宽速域乘波飞行器
本文选取的涡波一体宽速域乘波飞行器初始构型是基于定平面密切锥方法设计得到的[8],该类飞行器采用双后掠布局设计,因此又可称为双后掠乘波体.该类乘波体通过对平面形状的合理定制引入涡效应,可以在保持高超声速高升阻比的基础上低速性能不下降,兼顾了宽速域特性,为宽速域大空域的空天飞行器设计提供了新的思路.
图1 为涡波一体宽速域乘波飞行器的初始几何外形,表1 给出了初始构型的设计状态和相关设计变量.其中,该构型的第一后掠角为 λ1=75◦,第二后掠角为 λ2=50◦,长度l约4 m,翼展d=4.8 m,其设计状态为马赫数Ma=5,高度H=30 km,激波角为β=12◦.理论乘波体外形前缘尖锐,但实际应用过程中不可能实现.因此,本文采用文献[23]中的方法,将上表面抬高以对涡波一体宽速域乘波飞行器前缘进行钝化处理,钝化半径为r=2 mm.
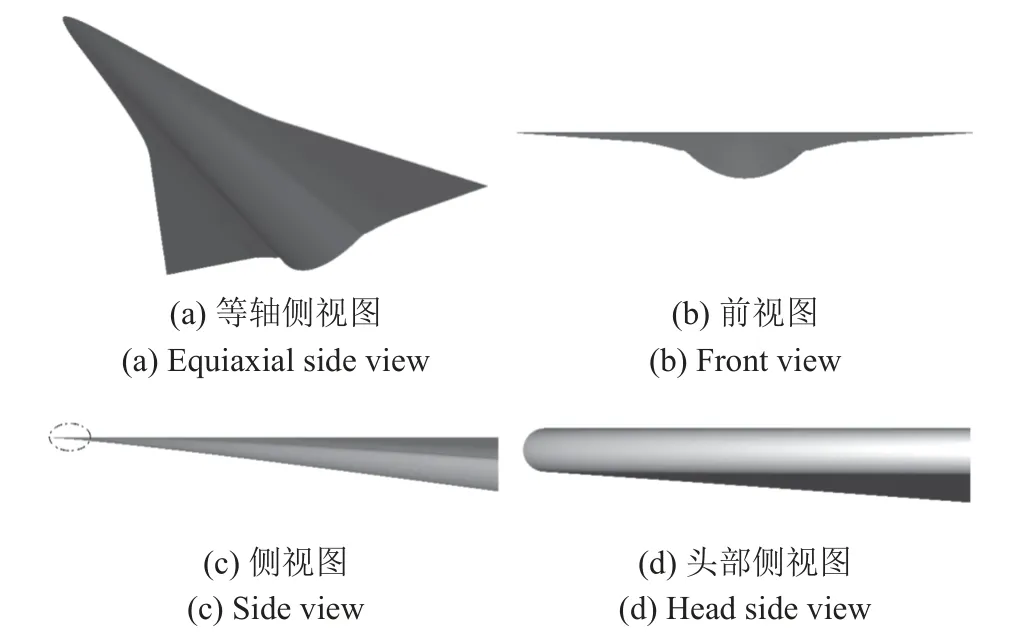
图1 涡波一体宽速域乘波飞行器初始构型Fig.1 Initial configuration of the wide-speed-range waverider with vortex-shock effects

表1 初始构型设计参数Table 1 Initial configuration design parameters
2 数值模拟方法及精度验证
2.1 数值模拟方法
数值模拟计算采用结构网格的RANS 求解器[24].该求解器基于MPI 并行计算,时间推进采用隐式LUSGS-GMRES 混合方法以保证定常流动求解的稳定性和收敛效率,空间离散方法采用二阶MUSCL重构方法以及“minmod”限制器,通量求解方法采用适用于全速域流动计算的HLLEMS 格式[25],湍流模型采用Spalart-Allmaras (SA)一方程模型.
2.2 数值模拟可靠性验证
由于本文的研究涉及宽速域飞行器的亚声速和高超声速条件下的气动特性,为了验证RANS 求解器的数值模拟精度,分别与亚声速和高超声速的风洞试验数据进行了对比.
2.2.1 亚声速流动数值模拟验证
亚声速条件下,参考第二次国际涡流实验(VFE-2)的三角翼几何模型的风洞试验数据[26],亚声速试验条件为: 自由来流马赫数Ma=0.4,雷诺数Re=6.0×107,迎角 α=13.3◦.数值模拟求解的计算状态与亚声速试验条件保持一致.图2 给出了三角翼流向两个不同站位处的压力系数分布对比.将数值模拟结果与风洞试验数据进行对比,可以看出两者的压力系数分布吻合良好.
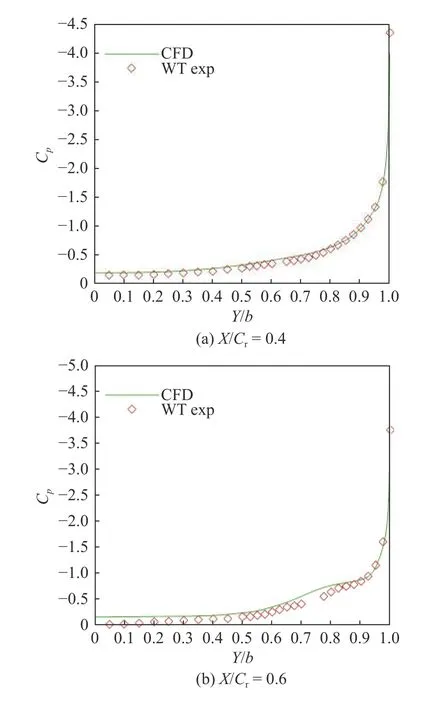
图2 低速条件数值模拟数据(CFD)与风洞试验数据(exp)对比Fig.2 Comparison between numerical simulation results (CFD) and wind-tunnel experimental (exp) datas at low speed
2.2.2 高超声速流动数值模拟验证
在高超声速条件下,针对双后掠乘波体试验模型开展设计马赫数状态的风洞试验,并对其进行数值模拟对比验证[27].其中,弯头双后掠乘波体的高超声速风洞试验条件为: 马赫数Ma=4.937,雷诺数Re=2.133×107,总压P0=1 008 575 Pa,总温T0=96.9 K.图3 给出了双后掠乘波体的数值模拟与风洞试验的气动力系数对比,可以看出不同迎角下的升力系数和阻力系数与风洞试验结果趋势保持一致.相比风洞试验,CFD 计算的气动力均略小,但两者的气动力系数相差均在3%以内.通过上述与风洞试验数据的对比验证,说明本文所采用的数值模拟方法是精确有效的.
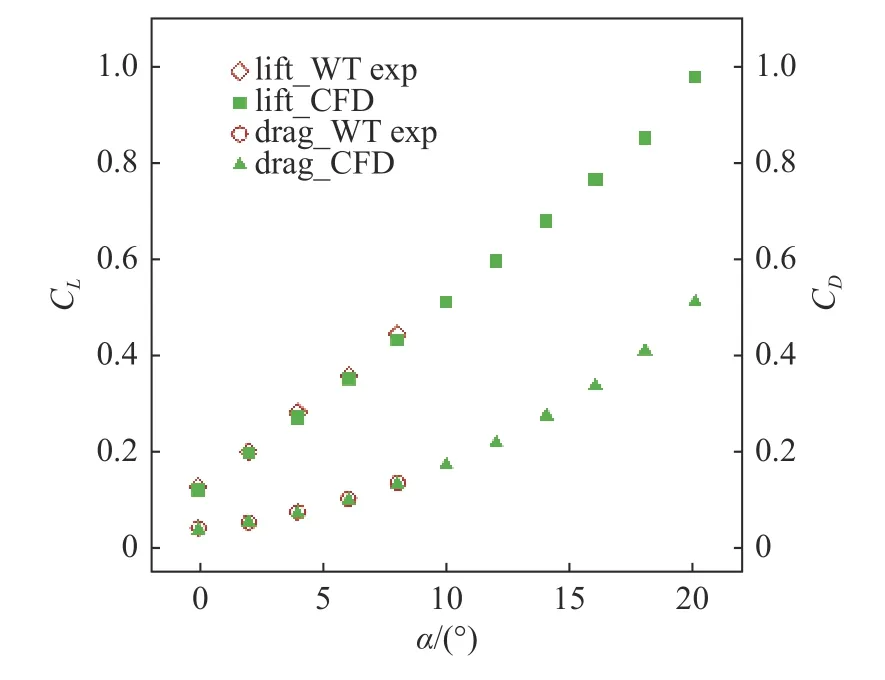
图3 高速条件数值模拟数据(CFD)与风洞试验数据(exp)对比Fig.3 Comparison between numerical simulation results (CFD) and wind-tunnel experimental (exp) datas at high speed
3 基于伴随的宽速域飞行器气动优化设计方法
3.1 伴随梯度求解及精度验证
采用离散伴随方程法求解梯度是该气动优化设计平台的核心,通过用式(1) 中目标函数F以及式(2)中控制方程残差R分别对设计变量x求导数,得到
然后将上式进行恒等变换得到
式中,x为设计变量,w为控制方程中的状态变量,如CFD 计算中的每个网格单元中的密度、速度等,对于任一给定的x都可以通过控制方程求解得到w,ψ为伴随算子,式(6)即为伴随方程.通过变换可将式(3)中耗时的 dw/dx求解转换为式(6)中的大规模线性方程组求解,具体可参考文献[28].
采用适用于高维设计变量的FFD 方法[29-30]对涡波一体宽速域乘波飞行器初始外形进行精细参数化,图4 给出了涡波一体宽速域乘波飞行器的FFD控制框.由于涡波一体宽速域乘波飞行器采用的是非传统的旋成体式前沿气动布局,这导致其表面是由一系列的光滑曲面组合而成,这些曲面的形状可以任意变化,即满足设计约束条件的布局外形具有较大的设计空间;另外,该类飞行器的气动特性对布局外形的变化也具有较高的灵敏度.因此,为更加精细地量化表征涡波一体宽速域乘波飞行器的初始外形,尽可能包含更广的优化设计空间,FFD 控制框半模共布置有15 个控制剖面,全模共29 个控制剖面.每个控制剖面沿流向上下表面各有17 个控制点,共34 个控制点.每个控制点只能沿Z向移动,用来对宽速域乘波飞行器的型面进行扰动.另外,为了保持前后缘线为初始型线,每个控制剖面上下表面沿弦向第一个和最后一个点保持不动.因此共有870 个FFD 控制点位移设计变量.

图4 涡波一体宽速域乘波飞行器FFD 控制框Fig.4 The FFD box of the wide-speed-range waverider with vortexshock effects
对FFD 控制点进行扰动,采用一组随机数选取15 个几何设计变量进行梯度信息求解精度验证.将伴随方程求解的升、阻力系数梯度信息与采用有限差分法计算得到的梯度值进行对比,有限差分步长为 1 ×10−4.两种方法求解得到的升、阻力系数对设计变量的梯度对比结果见表2 和表3.可以看出,基于伴随方程的梯度与有限差分结果吻合较好,相对误差范围在 1 0−3∼10−4,说明伴随方程法在求解梯度时具有较高的计算精度.
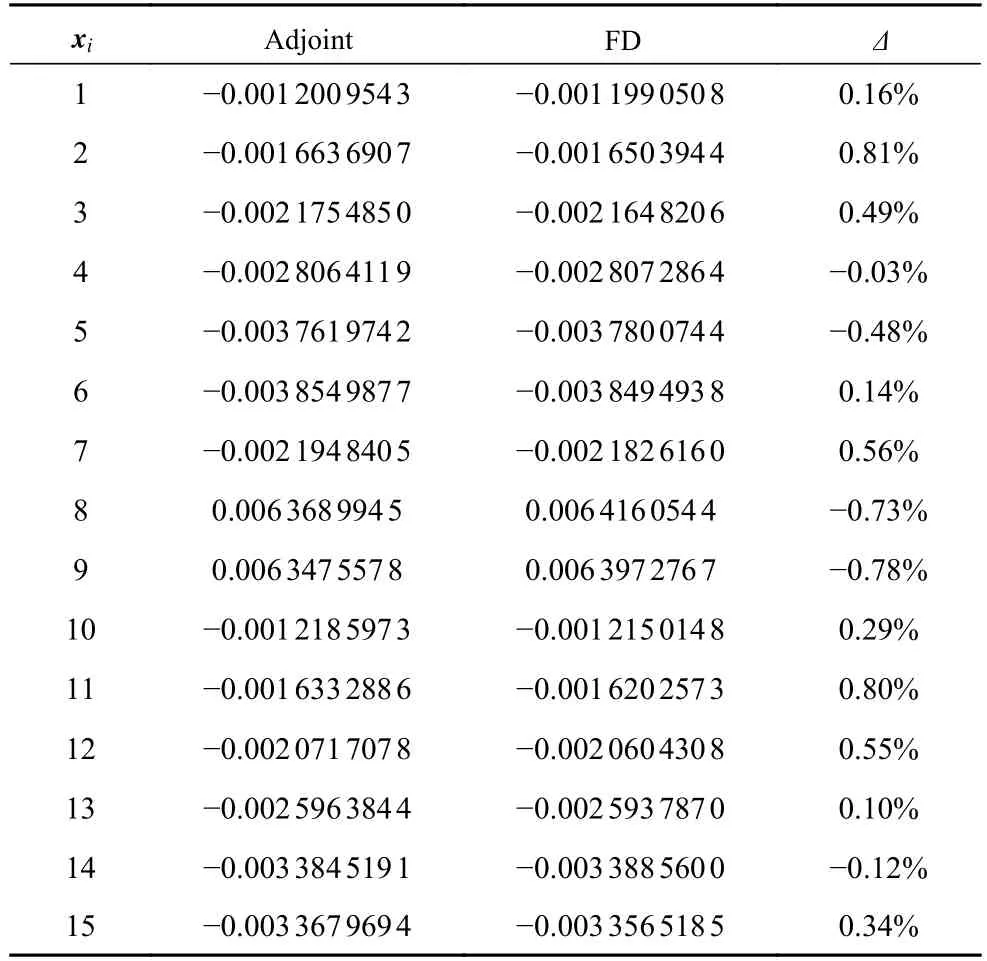
表2 伴随方法和有限差分法 CL 梯度计算结果对比Table 2 Comparison of the calculated gradient of C L between adjoint method and finite difference method
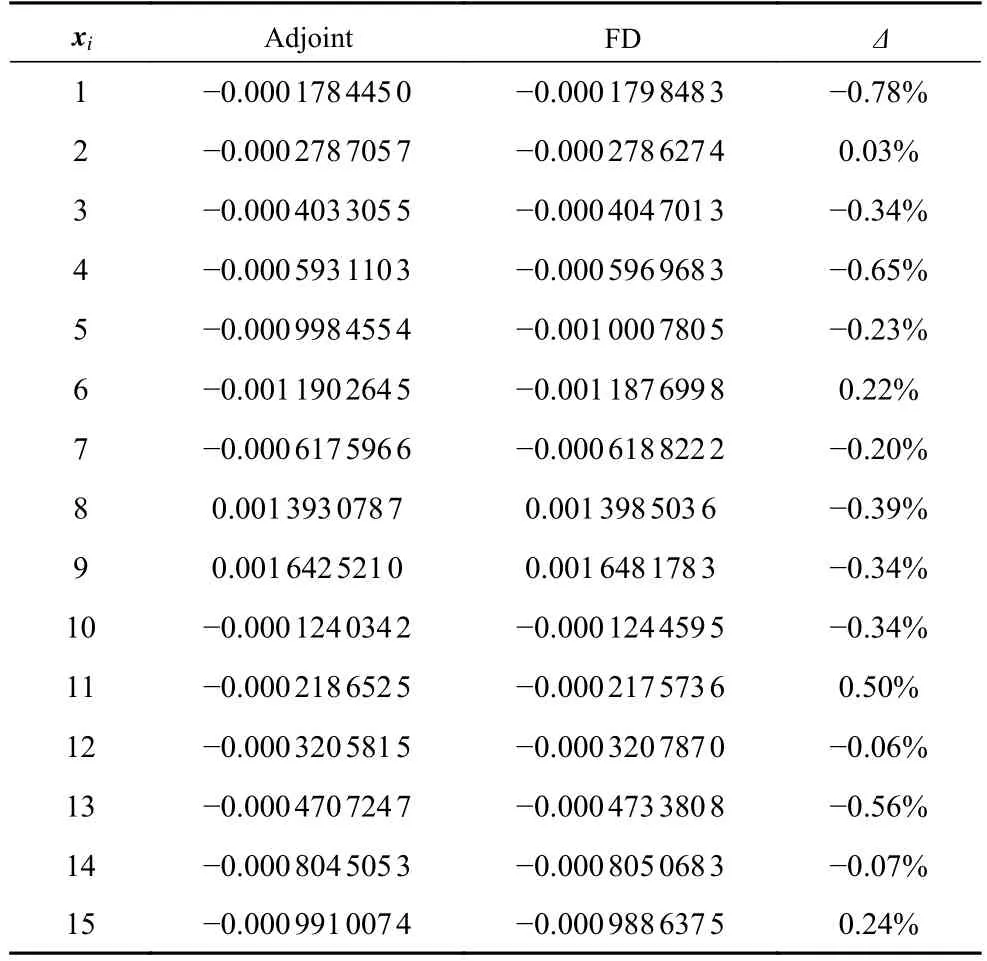
表3 伴随方法和有限差分法 C D 梯度计算结果对比Table 3 Comparison of the calculated gradient of C D between adjoint method and finite difference method
3.2 梯度优化设计平台
基于第二节中的RANS 流场求解器,通过结合适用于高维的FFD 参数化方法、鲁棒的结构网格变形方法、离散伴随方法和SQP 算法,在现有的基于离散伴随的高超声速飞行器气动优化设计平台[24]的基础上发展了宽速域气动伴随优化设计方法,其流程图如图5 所示.对于宽速域优化问题,首先,基于飞行器初始外形需分别生成在低速和高超声速状态下用于CFD 计算的空间网格;其次,需在低速和高速状态下分别进行CFD 流场计算;然后,可以将低速和高速的气动目标参数采用加权和方式组成单一目标函数,也可以将某一速域的参数作为优化目标,其余参数作为约束条件,本文采用的是加权求和方法.其中,不同权重因子的设置能够改变优化的侧重点,以达到期望的优化结果.
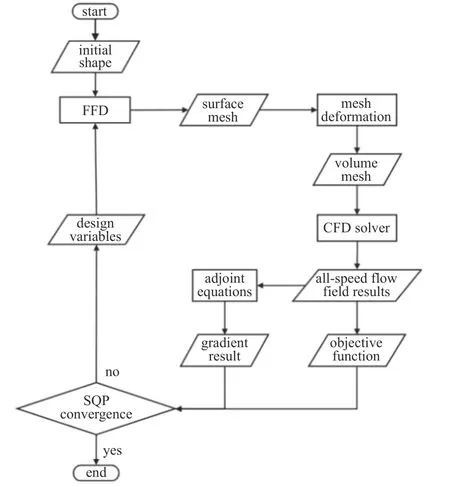
图5 基于离散伴随的宽速域飞行器气动优化设计方法流程图Fig.5 The flow chart of the aerodynamic shape optimization design software for the wide-speed-range vehicle based on the discretized adjoint method
4 兼顾低速与高超声速气动性能的宽速域飞行器优化设计
基于上文实现的宽速域飞行器离散伴随气动优化设计方法,本节针对定平面形状的涡波一体宽速域乘波构型开展了在最大升阻比工况下的三维整机宽速域气动优化设计.
4.1 优化设计问题
根据文献[8]可知,涡波一体宽速域乘波飞行器在低速和高超声速设计状态下最大升阻比对应的迎角在4°附近,因此,本文宽速域优化设计选取初始构型在最大升阻比点对应的工况分别为: 低速Ma=0.4,H=0 km,α=4◦,高超声速Ma=5.0,H=30 km,α=4◦.
优化问题的数学模型描述如下
由于宽速域优化设计需要评估外形的低速和高超声速气动性能,因此计算网格需要兼顾低速和高速的计算需求.本文根据优化设计需求设计了适用于高超声速环境和低速环境模拟的两套多块结构网格,网格如图6 和图7 所示.高速网格在激波间断处尽量顺激波方向,黏性层法向网格尽量保证垂直壁面,流向气流参数梯度较大处保证足够的流向网格密度.低速网格是在高超声速网格的基础上增大其边界跨度,其跨度约为初始外形长度的30 倍.
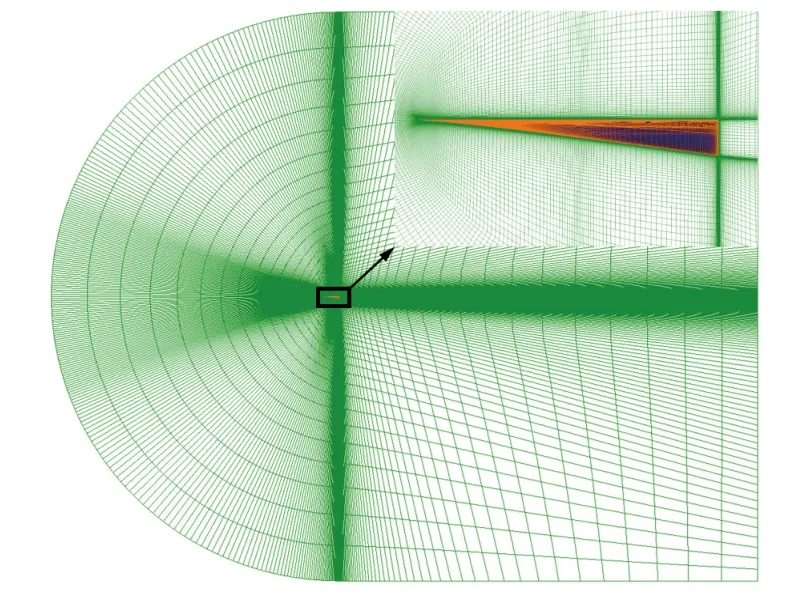
图6 低速计算网格Fig.6 Low speed computational grids

图7 高速计算网格Fig.7 High speed computational grids
采用粗、中、细三套网格对本文所选用的涡波一体宽速域乘波飞行器进行网格无关性验证,低速网格量分别是400 万、800 万和1100 万,高速网格量分别为210 万、400 万和700 万.表4 和表5 分别给出了在低速(Ma=0.4,H=0 km,α=4◦) 和高速(Ma=5.0,H=30 km,α=4◦) 下的网格无关性验证结果,图8 和图9 给出了三种网格在低速和高速状态下的表面压力系数对比.可以看到,粗网格和中网格的表面压力分布几乎一致,他们与细网格的阻力系数相对误差较小.因此,为保证优化设计过程中的计算精度和计算效率,本文选用粗网格进行宽速域气动优化设计.
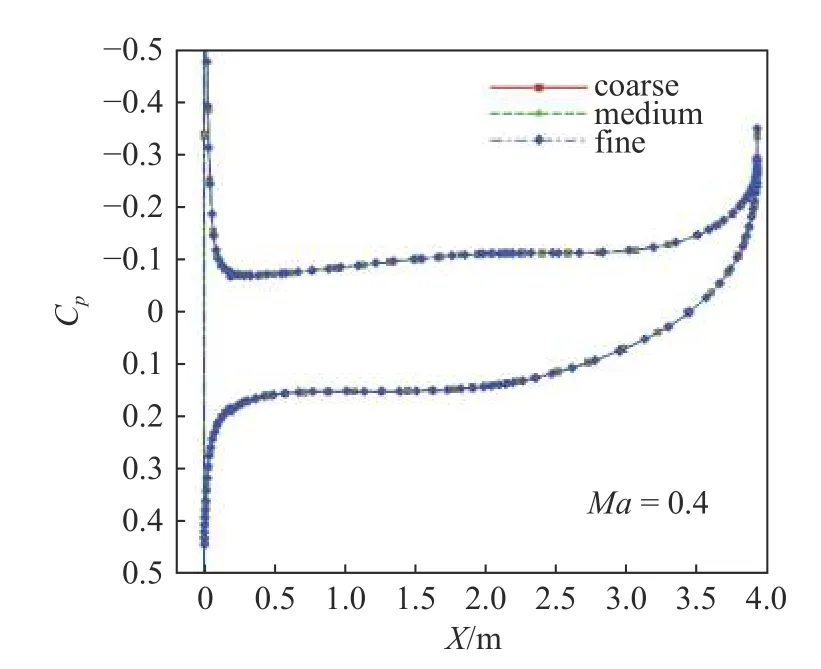
图8 低速对称面处表面压力系数对比Fig.8 Comparison of surface pressure coefficient on the plane of symmetry at low speed
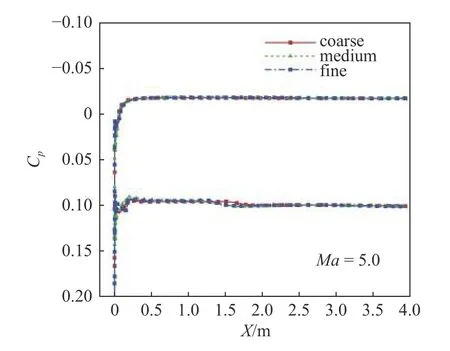
图9 高速对称面处表面压力系数对比Fig.9 Comparison of surface pressure coefficient on the plane of symmetry at high speed
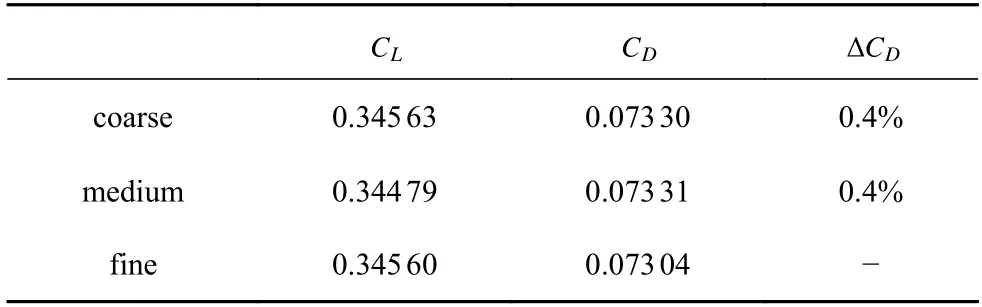
表4 低速网格无关性验证结果Table 4 The compute results of waverider at low speed
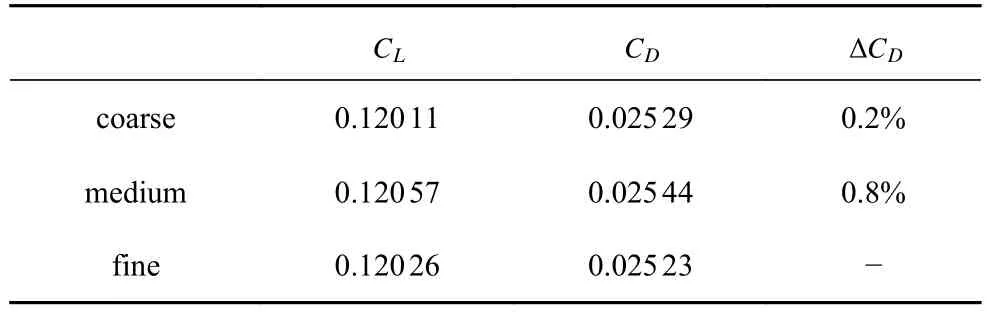
表5 高速网格无关性验证结果Table 5 The compute results of waverider at high speed
4.2 优化设计结果及分析
关于宽速域优化设计的计算效率,基于MPI 并行方法在56 核CPU(主频2.40 GHz)下开展整机优化设计,仅耗时约30 小时即完成10 次梯度优化迭代以及62 次流场求解,进而得到了收敛的优化构型.相较于初始构型,宽速域优化构型满足厚度约束且其容积有小幅增加,增加了近3%.图10 和图11 给出了宽速域优化迭代收敛历史.可以看出,优化中低速的升力和升阻比呈阶梯状上升,在第25 步之后,各速域升阻比变化趋于平缓.

图10 低速优化迭代收敛历史(H=0 km)Fig.10 Convergence history of the multi-point optimization iterations at low speed (H=0 km)
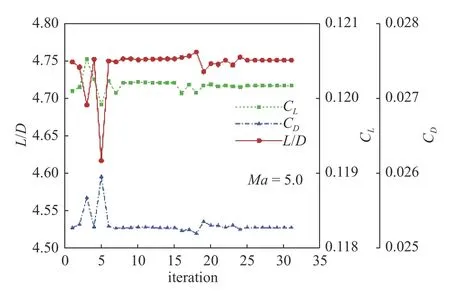
图11 高超声速优化迭代收敛历史(H=30 km)Fig.11 Convergence history of the multi-point optimization iterations at high speed (H=30 km)
表6 对比了宽速域优化前后不同状态对应的升阻力特性.可以看出,低速状态的升阻比大幅增加,提升了10.9%.优化效果的来源主要为升力的明显提升,提升了12.1%,阻力系数仅增加了8 counts.相对于初始外形,气动优化得到的外形可以在保持高超声速最大升阻比点具有良好气动性能前提下,显著提升低速最大升阻比点的整机气动特性.
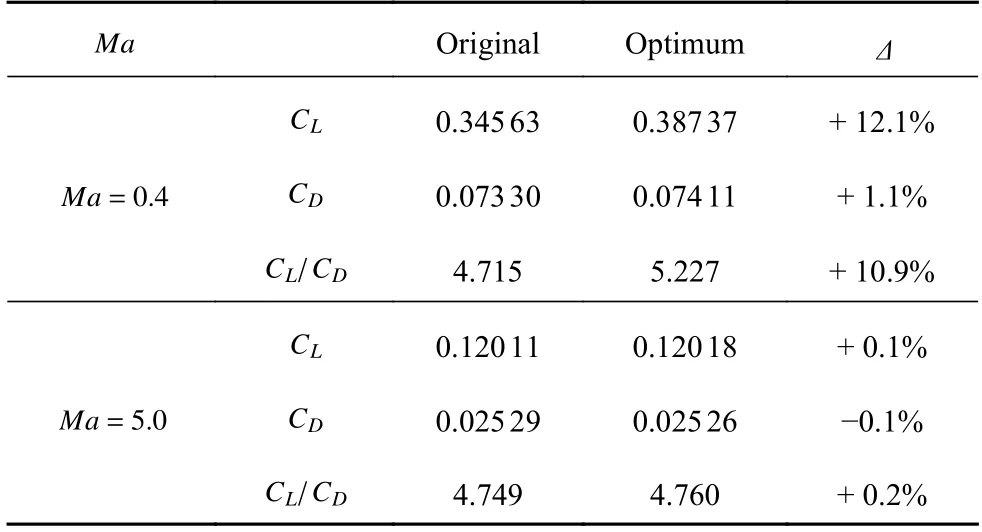
表6 优化前后升阻力特性对比Table 6 Comparison of the lift and drag characteristics
表7 给出了宽速域优化前后在不同状态下压心位置的变化情况.其中,CM为俯仰力矩系数的绝对值,力矩参考点为机头对应的坐标原点,xcp代表压心位置,即压心距头部的距离占全机长度的比例.可以看出,相较于初始构型,优化构型在低速和高速下的压心位置均有小幅后移,纵向静稳定性得到改善.低速状态下的压心位置变化相对明显,由于优化构型的升力增量主要来源于底部附近的表面压力变化,因此优化构型会产生更大的低头力矩,导致压心后移量较大.
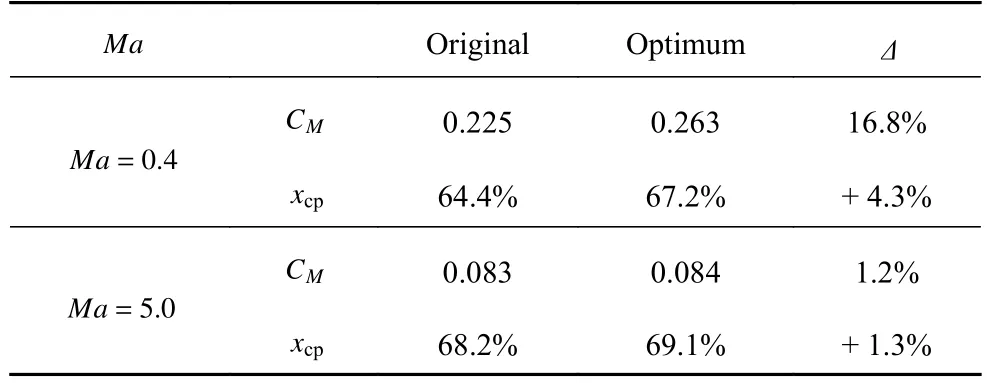
表7 优化前后压心位置变化情况Table 7 Comparison of the pressure center position
4.2.1 低速流场分析
图12 给出了涡波一体宽速域乘波飞行器优化前后低速背风面压力云图对比,同时也展示了低速空间涡结构对比.图13 给出了优化前后低速迎风面压力云图对比.从背风面压力云图可以看出,由于初始外形的双后掠设计,其在背风面两侧产生了强烈的旋涡结构,造成背风面前缘附近两片大范围的低压区,有效地提高了升力特性,从而使双后掠乘波体初始外形在低速下仍保持较好的气动特性,即涡波一体乘波飞行器的“旋涡效应”.该“旋涡效应”来源于初始外形本身的双后掠设计,在低速状态下可以通过类似大后掠前翼引起旋涡,并通过类似外翼部分的扰动增强旋涡[2].而通过宽速域优化设计得到的优化外形进一步增强了双后掠乘波体的“旋涡效应”,相较于初始外形,优化外形前翼引起的旋涡强度增强,背风面低压区面积增加;外翼的扰动也更强,尤其是靠近底部的外翼部分,前缘涡向对称面扩展直至中部,背风面附近流速加快,造成低压区面积更大,从而使得优化外形升力大幅提升,显著改善其气动特性.从迎风面的压力云图同样也可以看出,优化外形通过型面变化使得第一后掠角和第二后掠角交接处沿前缘向后延伸的高压区域范围增大,同时也改善了底部附近的低压区范围,使得迎风面提供的升力有所增加.
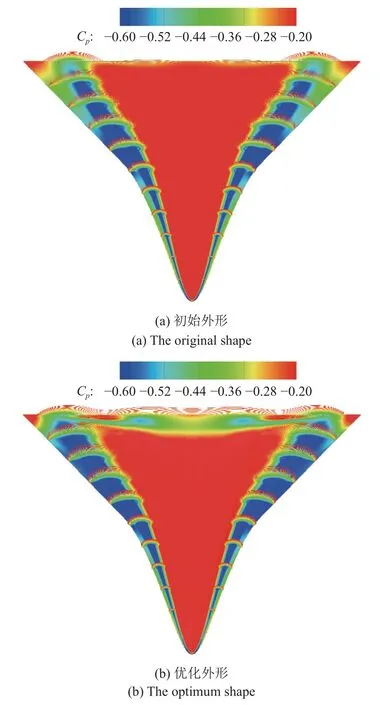
图12 优化前后低速背风面压力分布涡结构对比(H=0 km,Ma=0.4)Fig.12 Comparison of Cp distribution and vortex structure on the upper surface before and after optimization at low speed (H=0 km,Ma=0.4)
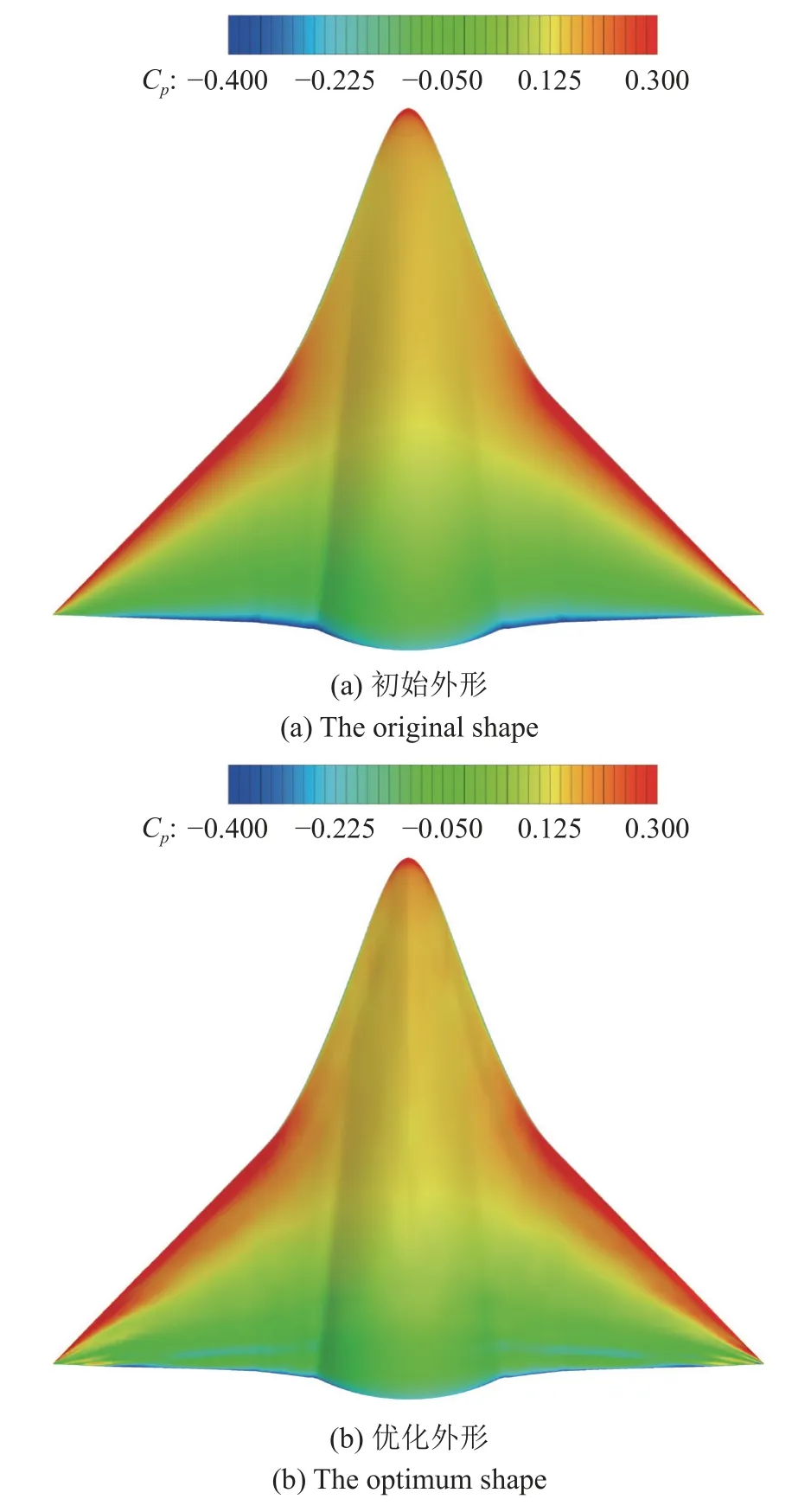
图13 优化前后低速下表面压力分布对比(H=0 km,Ma=0.4)Fig.13 Comparison of Cp distribution on the lower surface before and after optimization at low speed (H=0 km,Ma=0.4)
图14 给出了流向各截面位置,图15 给出了优化前后流向各截面表面压力系数分布与几何外形对比.从流向各站位可以看出,由于前缘引起的旋涡,背风面前缘附近的表面压力分布出现突变,明显减小.优化外形背风面在靠近前缘处向上凸起,使得涡结构向前缘移动,表面低压区同时也向外侧扩展,因此,优化外形背风面前缘附近的压力更小.在靠近底部附近,由于优化外形上下型面均出现先上凸后下凹的变化,在靠近对称面处出现第二个吸力峰值,但型面存在凹坑,导致背风面出现局部高压区.另外,优化外形前缘下移,相对厚度减小,外翼的扰动更剧烈,迎风面压力出现较大波动.
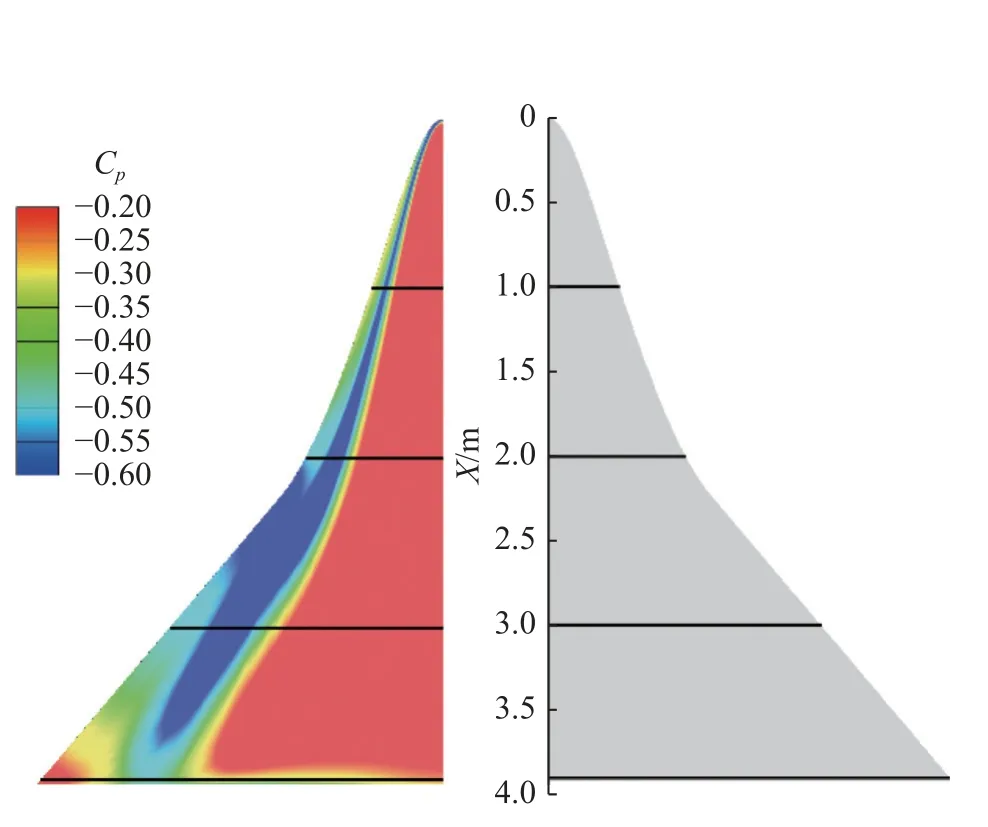
图14 流向各截面位置Fig.14 Four stations of the initial configuration
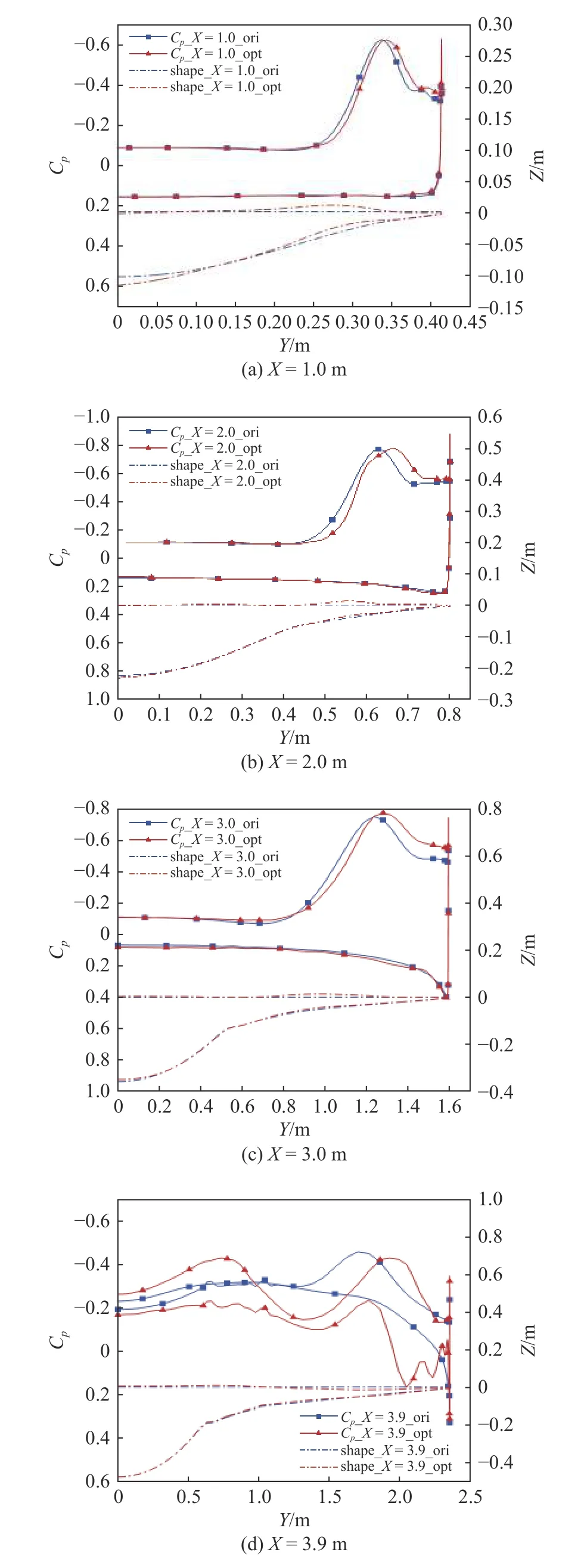
图15 优化前后流向各截面表面压力系数分布与几何外形对比(H=0 km,Ma=0.4)Fig.15 Comparison of the Cp distribution and shape before and after optimization (H=0 km,Ma=0.4)
已有研究表明,用Q准则[31]来判别涡的结构具有较高的精细度和可靠性[32],因此本文利用Q值来判别乘波飞行器背风面产生的旋涡强度,其中,满足Q值为正的等值面即为涡环.图16 给出了优化前后的涡强度云图对比.可以看出,外翼扰动产生的涡较前翼涡形状更加扁平,同时,由于第二后掠角较小,外翼产生的涡强度更低.相较于初始外形,优化后外形在前缘附近向上凸起,使得涡结构向外侧平移,且更加贴近物面,前翼与外翼产生的涡强度均有小幅增强.同时,优化外形背风面在底部附近也出现强度较小的涡结构,从而使得背风面靠近对称面处的压力有所降低.
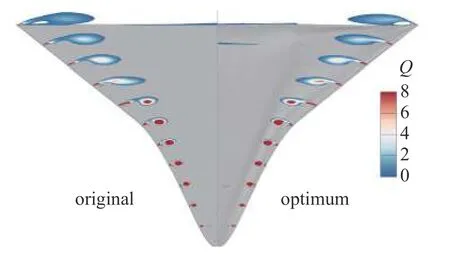
图16 优化前后涡强度对比Fig.16 Comparison of Q value before and after optimization
针对优化前后压力变化明显的区域,进一步开展流场分析.图17 给出了优化前后底部附近的涡强度云图对比,图18 给出了优化前后Q=2等值面图.可以看到,由于优化外形型面的变化,其背风面产生了强度较小的涡结构,在靠近对称面处也形成了一个低压区,会额外提供一部分升力.从Q=2等值面图可以观察到,初始外形自机头拖出的前缘涡(第一后掠角)与第二后掠角之后的外翼涡并未完全交汇,而优化外形的头部前缘涡与外翼涡更加靠近前缘,且两者与前缘处的分离气流完全交汇并相互缠绕在一起,前缘涡中的流速更快.因此,优化外形产生的前缘涡具有较高的强度,其表面压力也相对较低.

图17 压力变化明显处涡强度对比Fig.17 Comparison of Q value in the area of obvious pressure change
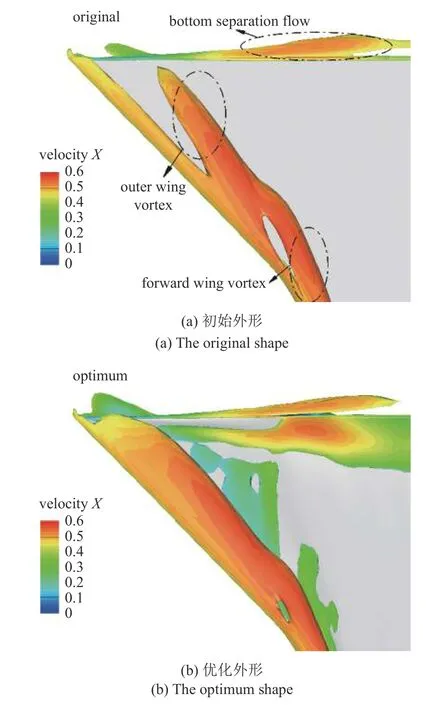
图18 优化前后 Q=2 等值面速度云图Fig.18 Iso-surface of Q=2 before and after optimization
图19 给出了背风面压力明显变化区域的流向各截面位置,图20 给出了X=3.5 m 至X=3.8 m 截面处的表面压力系数分布和外形对比.可以看出,在优化外形的中后部,其靠近对称面处的背风面均有不同程度的上凸.由于型面的变化,对附近的气流产生扰动,气流速度加快,即上文提到强度较小的涡结构,因此,优化外形背风面在该区域的压力较小.另外,优化外形靠近前缘处的背风面出现下移,导致外翼涡更加靠近前缘,吸力峰值也向外侧移动,同时,由于前缘涡具有较高的强度,优化外形的表面吸力峰值也更高.
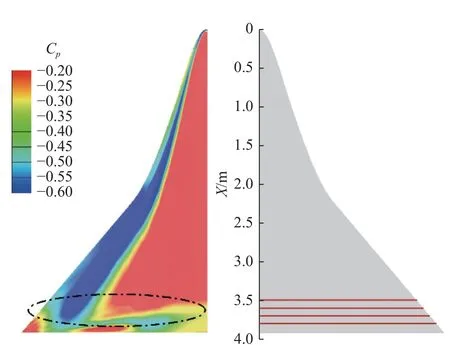
图19 压力明显变化区域流向各截面位置Fig.19 Four new stations in the area of obvious pressure change
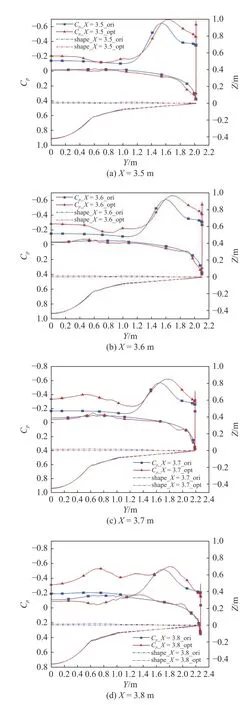
图20 优化前后流向各截面表面压力系数分布与几何外形对比(H=0 km,Ma=0.4)Fig.20 Comparison of the Cp distribution and shape before and after optimization (H=0 km,Ma=0.4)
综上所述,在低速状态下优化后外形背风面产生的旋涡强度较强,背风面压力明显下降,迎风面压力增加,尤其是靠近底部的区域.因此,优化后外形在低速状态下的升力及升阻比均提升明显.
图21 给出了宽速域优化外形与初始外形升阻比随迎角的变化情况.可以看出,相较于初始外形,优化外形背风面的旋涡效应进一步增强,使得飞行器在低速中小迎角状态的升阻特性得到明显提升.但是,在大迎角状态,宽速域优化外形的阻力略微增加,导致优化后升阻比增量有所减小,后续工作将进一步开展考虑低速大迎角性能的宽速域气动优化设计研究.
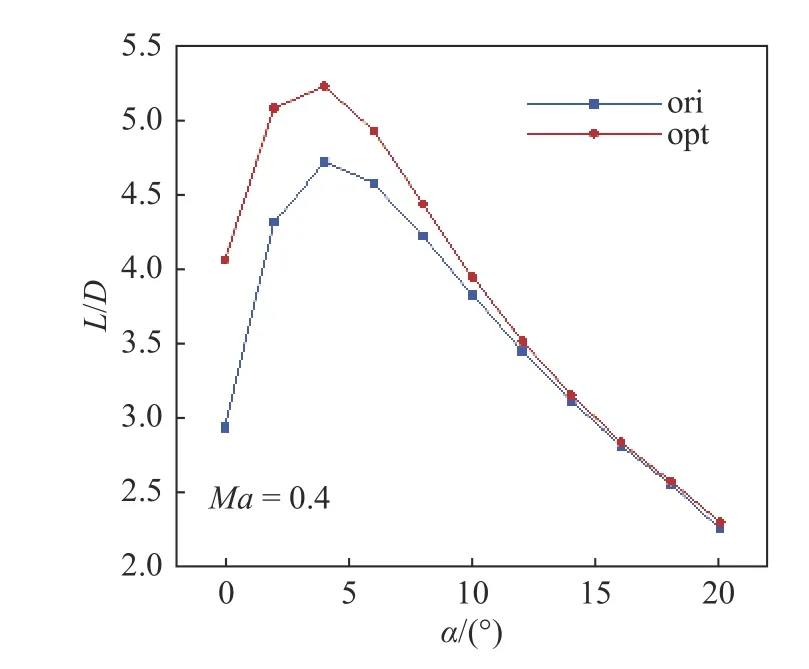
图21 优化前后低速升阻比随迎角变化Fig.21 The lift drag ratio with angle of attack at low speed before and after optimization
4.2.2 高速流场分析
图22 和图23 分别给出了涡波一体宽速域乘波飞行器优化前后高超声速迎风面压力系数和空间流场对比.可以看出,初始外形在前缘线附近存在明显的高压区,且在第二后掠区域的类似外翼翼根部位也存在大片高压区.相较于初始外形,优化后外形使得头部前缘线附近的高压区域转移到了中间附近,同时在第二后掠区域外翼翼根附近的高压区范围有所减少.但优化外形在靠近底部的外翼段压力有所提升,因此,优化外形的升力特性并没有明显下降.由于该乘波飞行器初始外形是基于二维无黏理论假设设计得到的,并对前缘进行钝化处理,因此,其在进行黏性计算后前缘会出现不同程度的溢流.而优化后的外形抑制了背风面前缘附近的溢流量,特别是在外翼段,前缘处的高压气流能更好地被限制在迎风面.
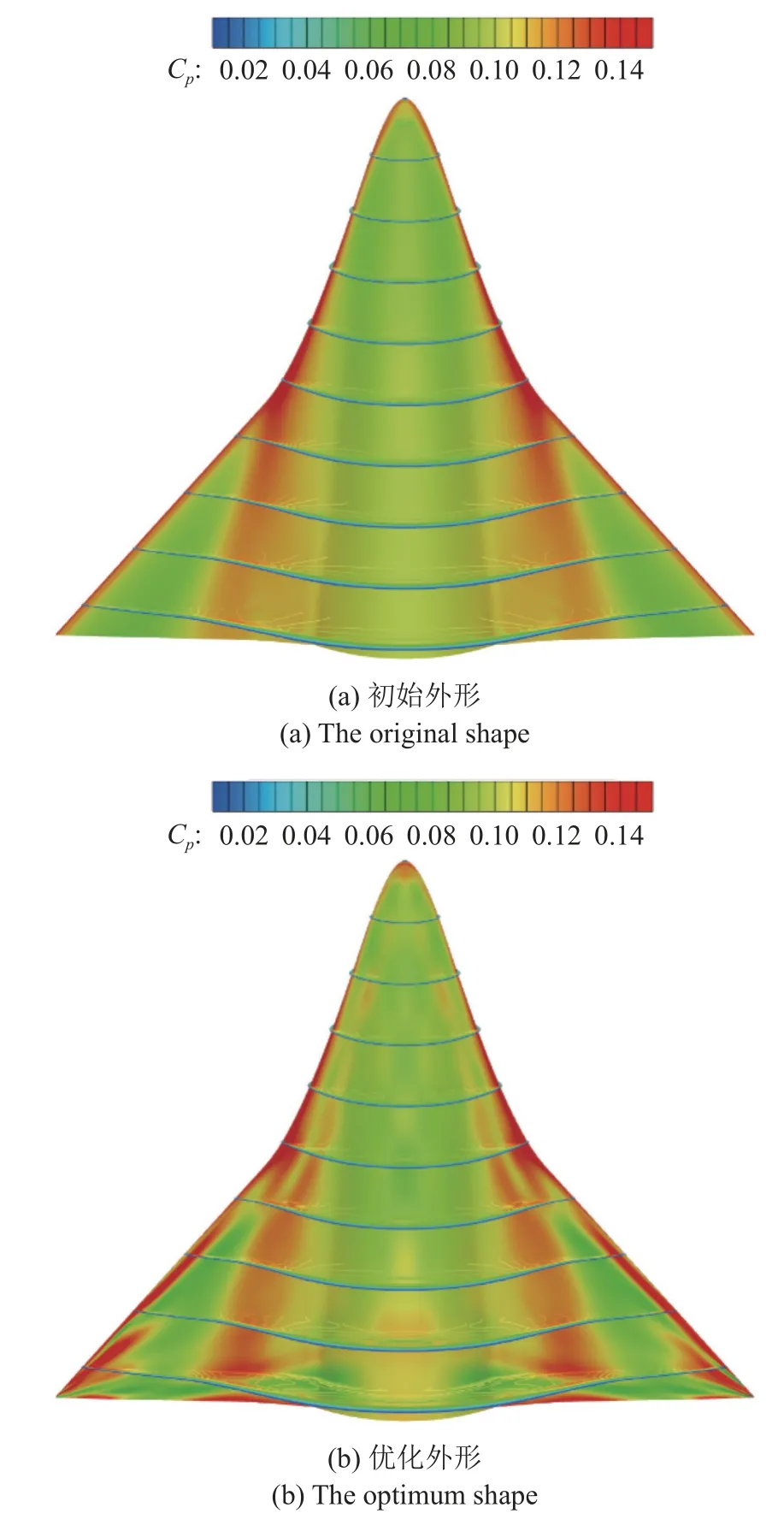
图22 优化前后迎风面压力分布对比(H=30 km,Ma=5.0)Fig.22 Comparison of Cp distribution on the lower surface before and after optimization at high speed (H=30 km,Ma=5.0)
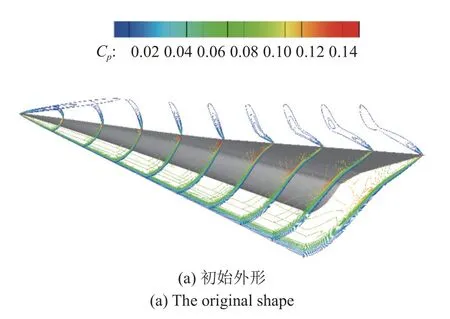
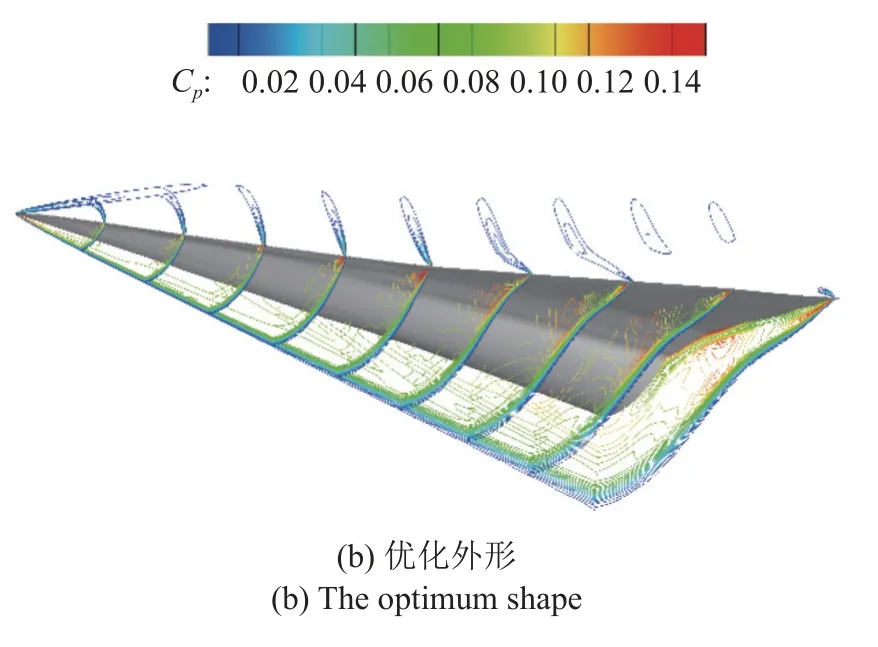
图23 优化前后空间流场对比(H=30 km,Ma=5.0)Fig.23 Flow field changes of the wide-speed-range waverider before and after optimization (H=30 km,Ma=5.0)
图24 给出了优化前后高超声速下流向各截面处表面压力系数分布曲线和外形对比.通过表面压力系数分布曲线和外形对比同样也可以发现,在第一后掠头部附近,优化后外形在靠近前缘处,虽然迎风面相对上移,但背风面同时也有所上凸,因此物面角仍相对较大,激波强度依然较强,导致压力有所增加.在双后掠乘波体的中后部,由于优化后型面的局部变化,在类似翼根处迎风面出现局部膨胀波和二次激波,使得底部附近迎风面压力有所增加,对升力特性进行补偿.综上,相较于初始外形,优化后外形虽在迎风面局部压力有所下降,但整体来看,其在高超声速下的升阻特性仍有小幅提升.
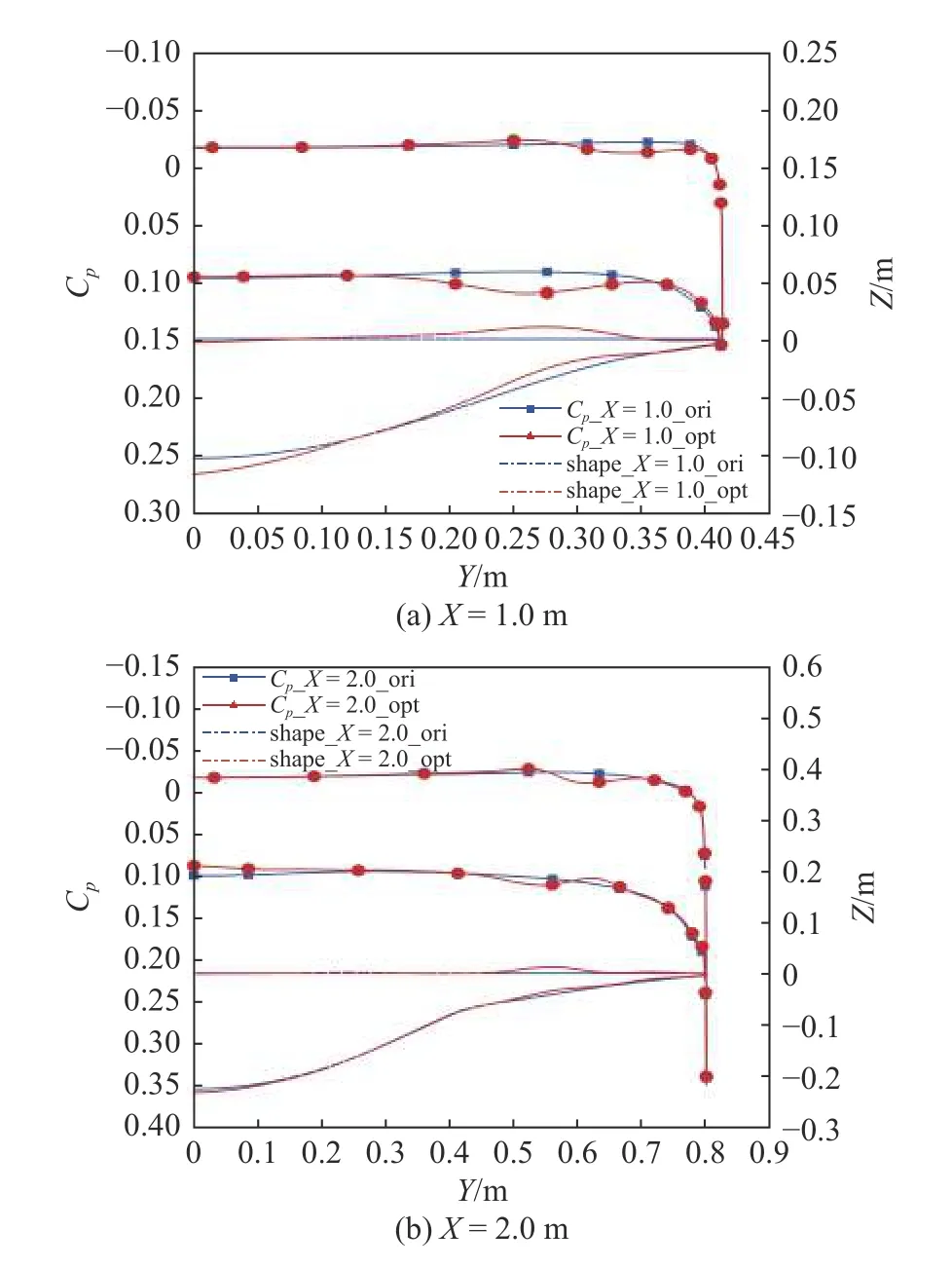
图24 优化前后流向各截面表面压力系数分布与几何外形对比(H=30 km,Ma=5.0)Fig.24 Comparison of the Cp distribution and shape before and after optimization (H=30 km,Ma=5.0)
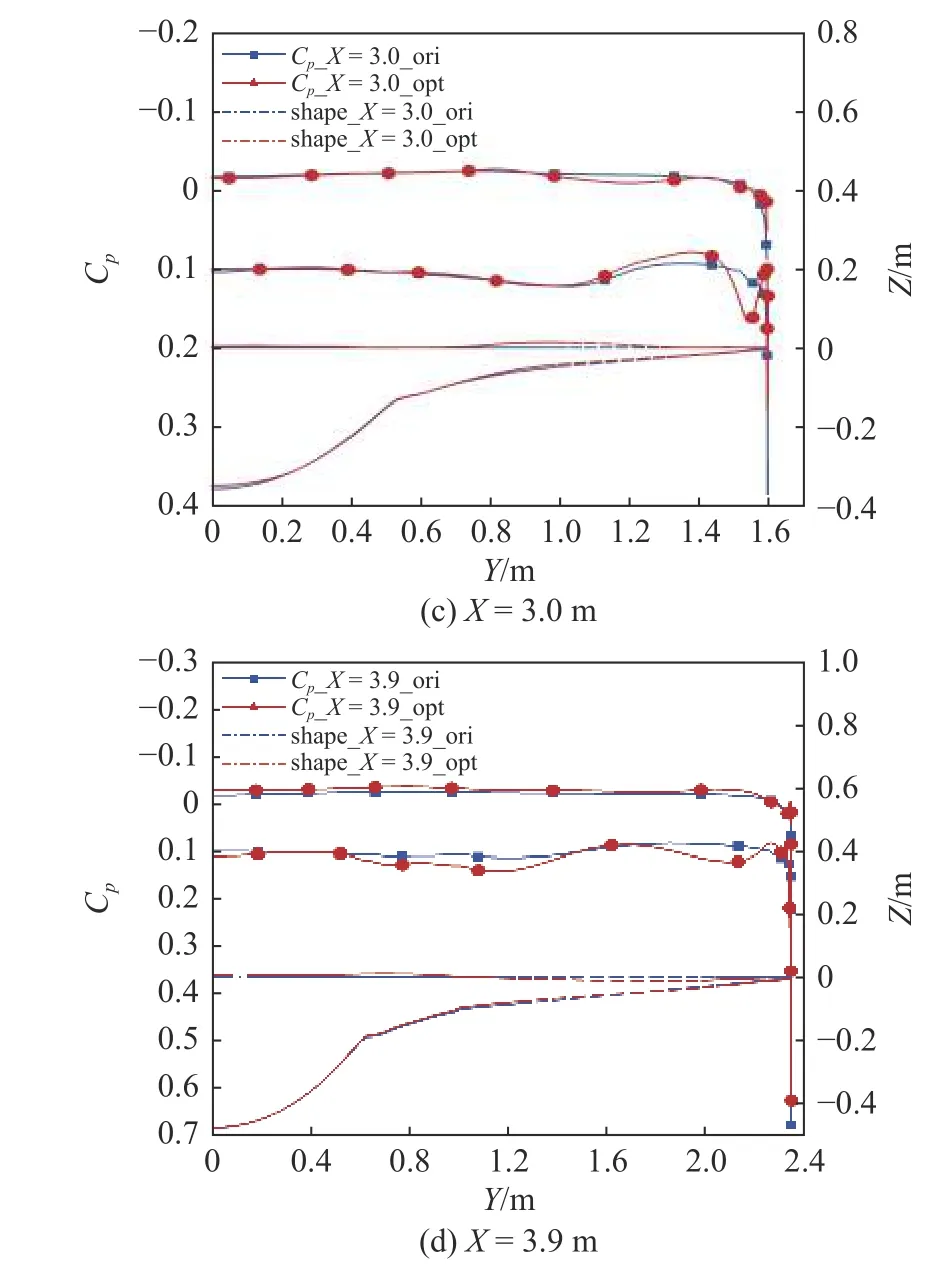
图24 优化前后流向各截面表面压力系数分布与几何外形对比(H=30 km,Ma=5.0) (续)Fig.24 Comparison of the Cp distribution and shape before and after optimization (H=30 km,Ma=5.0) (continued)
5 结论
针对三维复杂飞行器整机的宽速域气动设计问题,本文在现有的基于离散伴随的高超声速飞行器气动优化设计平台的基础上,发展得到了鲁棒高效的宽速域气动伴随优化设计方法.基于该方法,针对涡波一体乘波飞行器开展了兼顾低速和高超声速气动性能的宽速域三维整机优化设计研究.研究结论如下.
(1) 针对涡波一体乘波飞行器的宽速域气动优化设计表明,伴随优化方法在针对大规模设计变量的宽速域飞行器开展气动优化时仍具有较高的效率,具体为,在低速和高超声速两套多块结构网格(网格量分别为400 万和210 万),870 个设计变量以及304 个设计约束条件下,该方法仅花费1680 CPU(2.40 GHz)小时即完成多速域的整机气动优化设计.
(2) 涡波一体乘波飞行器在宽速域优化后,可以在保持高超声速状态良好的气动性能前提下,低速状态的升力与升阻比有明显提升,均提升了10%以上.
(3) 低速状态下,优化外形使得前缘涡向外侧移动,外翼的扰动更强,进一步增强了涡波一体乘波飞行器的旋涡效应.同时,底部前缘涡向内侧扩展,在靠近对称面处也产生较弱的旋涡,造成背风面低压区面积更大.此外,迎风面底部附近的低压区范围也得到改善,从而使得低速下的升力大幅提升.
(4) 伴随优化方法可有效应用于宽速域飞行器的气动优化设计研究,研究结果具有一定的工程指导意义.
相对初始外形,宽速域优化设计得到的气动外形型面出现凹凸变化,使得低速大迎角下的阻力增加,优化收益有所下降;此外,其对结构热防护与弹性设计也会带来一定难度.后续研究工作中,将进一步开展考虑低速大迎角性能的宽速域优化设计以及评估宽速域优化外形的热环境与弹性变化.

