基于虚拟区域法的黏弹性流体中微生物游动的数值模拟和应用1)
彭方远 潘定一 陈杏藩 林昭武,2)
* (浙江大学工程力学系,杭州 310027)
† (浙江大学光电科学与工程学院,杭州 310027)
引言
研究微生物游动的行为特征以及动力学机理,具有重要的理论意义和应用价值.微生物作为自然界生态系统的重要组成部分,分解各种有机物,直接参与物质循环,例如海洋中的微生物为全球提供了大量的氧气,供人类生产生活[1].此外,细菌类微生物聚集能够形成生物膜,可以利用其进行废水处理,但也容易造成食品污染等不利后果[2].随着科学技术的飞速发展,模仿微生物的人工微型器件广泛应用于各个领域.例如Karshalev 等[3]利用涂有二氧化钛的“镁微球”,证明了铁和硒矿物质可以用于治疗贫血.Zhang 等[4]利用“微型器件”监测传感电化学信号,并应用于临床诊断、药物运输等方面.Vyskočil等[5]利用“微型机器人”,可以在不破坏细胞膜的情况下进入癌细胞,拓展了癌症的治疗方法.由此可见,深入研究微生物的行为特征,了解并掌握微生物在复杂流体中的运动特性,具有重要研究价值,并且可以为微型器件的设计制造提供理论指导.
鉴于以上原因,微生物游动问题受到越来越多的关注.其中,壁面效应是微生物游动研究中的重要问题之一.已有研究表明,微生物在壁面附近存在复杂的行为特征[6-14],例如: 团藻在壁面附近的“跳舞”行为,公牛精子和衣藻在近壁处的散射行为,大肠杆菌在固壁面附近沿顺时针绕圈的行为[6-8].Kuron 等[9]采用数值方法研究牛顿流体中微生物在平面以及曲面壁面附近的行为特性,发现了散射、向前翻滚、向后翻滚和悬停等四种行为.Chaithanya 等[10]初步分析了壁面曲率对微生物行为的影响规律,其结果表明牛顿流体中微生物更容易被凹形曲面吸引.Ishimoto 等[11]的研究结果表明,牛顿流体中壁面的拓扑结构对于引导微生物的定向运动有一定的作用.Narinder 等[12-13]采用实验手段,利用人工合成感光粒子模拟微生物,发现与牛顿流体相比,粒子在黏弹性流体近壁处的速度明显减小;而且由于流体弹性,粒子会绕开弯曲壁面.Li 等[14]采用数值方法,研究了黏弹性流体中微生物近壁处的行为特征,发现不同类型微生物具有不一样的运动特性.Ouyang等[15]采用浸没边界−格子波尔兹曼方法,研究了幂律流体中微生物近壁处的行为特性,发现随着幂律流体指数的变化,不同种类的微生物表现出的行为特性具有一定的差异性.Ahana 等[16]采用数值模拟的方法,研究发现与非近壁相比,微生物在近壁处的平动速度较少,而角速度却较大.Leoni 等[17]实验研究了两种不同类型的微生物在曲壁面附近的行为特性,发现了三种形态,且微生物都更为集中地在壁面附近运动.Yazdi 等[18]运用数值方法研究了Oldroyd-B流体中微生物的游动行为,发现微生物与壁面的初始距离对微生物壁面效应有较大影响.
总体而言,已有研究工作大多集中于牛顿流体领域,仅有少数涉及黏弹性流体等非牛顿流体领域.这主要是因为: 一方面黏弹性流体等非牛顿流体的流动行为比较复杂;另一方面求解黏弹性流体本构方程具有一定的难度,对算法精度和稳定性都有很高的要求[19].
对于算法稳定性,已有文献提出显式求解、迭代求解、额外增加人工耗散项以及限制构型张量特征值等方法[20-23].对于对流项的离散,为了保证其精度,已有研究工作提出迎风格式、TVD(total variation diminishing) 格式、MUSCL(monotone upstreamcentered schemes for conservation laws)格式以及WENO(weighted essentially non-oscillatory)格式等[24-26].对于构型张量的求解,文献中提出了对构型张量进行一系列的变换以保证其对称正定性质,如:对数函数变换、平方根分解以及乔列斯基分解等[23,27-28].上述方法一定程度上保证了算法的精度以及稳定性.但是,文献[19] 同样指出,对于高Reynolds 数以及大Weissenberg 数的工况,现有数值算法仍面临巨大的挑战.
有鉴于此,本文对求解黏弹性流体的数值算法进行初步探索,并将其应用于研究微生物游动过程的壁面效应.本文余下内容组织如下: 第1 节介绍数学模型以及数值算法;第2 节进行算法验证;第3 节给出模拟结果并进行机理分析;最后第4 节给出本文结论以及后续工作展望.
1 模型和方法
本文所模拟的对象涉及运动边界等问题,为了处理相应的流固耦合问题,本文采用虚拟区域方法(fictitious domain method),将问题分解为流体子问题、微生物运动子问题以及黏弹性流体本构方程子问题进行求解.总体而言,在模型方面,微生物运动采用经典的Squirmer 模型,而黏弹性流体则采用Giesekus 模型;在黏弹性流体本构方程的数值求解方面,则采用显式格式结合乔列斯基分解进行求解.以下分小节详细介绍.
1.1 微生物模型
Squirmer 模型是一种经典的微生物水动力模型,最早由Lighthill[29]和Blake[30]提出.该模型将微生物视为球形刚性颗粒,其表面具有给定的速度分布
式中e为颗粒的游动方向,r为径矢,Pn为n阶勒让德多项式(Legendre),n为阶模态系数.与大多数已有文献相同,本文采用前两阶模态,即
其中,角度 θ=arccos(e·r/r),表示位置径矢与运动方向的夹角;B1和B2是前两阶模态的系数.通过比值U0=2B1/3 来区分粒子的类型,β >0时为拉动型粒子(puller),β <0 时为推动型粒子(pusher),β=0时为中性粒子(neutral).在Stokes 流中,粒子的稳定游动速度为U0=2B1/3.
由于采用虚拟区域方法进行数值模拟的缘故,需要将式(2)延拓到整个球体,于是采用Li 等[31-33]提出的速度分布模型
其中a是球型颗粒的半径,er和eθ是沿r和θ方向的单位向量,m是任意正整数.当r=a时,式(3)符合式(2)的速度分布.
1.2 流体黏弹性模型
本文采用经典的Giesekus 黏弹性本构模型[34],黏弹性流体中聚合物的应力贡献为
其中 λt表示聚合物的弛豫时间,µp表示聚合物黏度,C为构型张量,具有对称正定性质.构型张量的本构方程为
其中 α为模型参数,表征聚合物受到的各向异性水动力,其取值范围为 0 ∼0.2.α=0时,Giesekus 模型退化为黏度为常数的Oldroyld-B 黏弹性模型.方程(5)的求解难点在于: (1)方程的非线性性质;(2)保证构型张量C的对称正定性质;(3)对流项的离散.其求解方法将在1.4 数值格式部分详细介绍.
1.3 虚拟区域法
虚拟区域方法属于非贴体网格法,最早由Glowinski 等[35]提出,其核心思想是假设固体颗粒内部充满虚拟流体,对内部的虚拟流体作用一个拟体力(也称为拉格朗日乘子),使其运动满足刚体运动的约束.在此基础上Yu 等[36-37]发展了虚拟区域方法,提出了直接力格式,并将算法并行化.文献[37-40]将该方法应用于研究颗粒湍流问题,并取得了一系列进展.近年来,本文作者Lin 等[33]进一步拓展该方法,将其成功应用于研究牛顿流体中微生物的游动问题.虚拟区域法求解的无量纲形式的控制方程如下
1.4 数值格式
在求解流体控制方程时,本文采用时间步分裂格式[33,36],将方程式(6)~ 式(11)解耦为流体运动、微生物颗粒运动以及黏弹性流体本构方程等三个子问题.
(1)流体运动子问题,求解u∗和pn+1
采用投影格式将速度和压力解耦求解上述方程组,即
①速度亥姆霍兹(Helmholtz)方程
②压力泊松(Poisson)方程
③速度和压力修正方程
流场采用半交错均匀网格,空间导数离散采用二阶中心差分格式;速度方程(14) 与压力方程(15)采用多重网格迭代法进行求解.
将方程式(18)~ 式(19)代入式(20)~ 式(21)可以得到
最后,流体速度求解如下
上述方程的求解,涉及物理量在不同网格间的转换.本文采用三线性插值函数作为离散Delta 函数实现物理量在欧拉网格节点x和拉格朗日网格节点X之间的转换.
式中h为网格步长,ψ函数为线性函数
(3)黏弹性流体本构方程子问题,求解Cn+1
记构型张量及速度的分量形式为
本文采用Vaithianathan 等[23]提出的数值方法求解黏弹性流体本构方程(11).利用乔列斯基方法分解构型张量C可以得到
将构型张量C的求解转化为对张量L的求解,只要张量L的对角元素满足条件l11,l22,l33>0,即可保证其对称正定性质.进一步对对角元素采用指数函数替换
将式(28)和式(29)代入方程(11),可以得到
利用已更新的速度un+1,对新方程(30)采用显式求解.对流项采用高精度的MUSCL 格式离散;时间积分采用四阶龙格库塔方法;从而保证算法具有良好的数值精度以及稳定性.
1.5 碰撞模型
本文研究的问题还涉及微生物颗粒与平面壁面的接触问题,因此引入软球碰撞模型,对壁面附近的刚体颗粒施加一定的排斥力,从而使得颗粒与壁面之间避免重叠.该模型如下[33,37]
其中F0为给定常数,d是颗粒与壁面间的距离,dc是判断“接触”与否的截断距离,n是接触方向的单位向量.本文设置F0=1.0×(104∼105),dc=h∼2h.最后更新颗粒位置
由于方程式(31)~ 式(32)采用显式求解,所以要求更小的时间步长,本文选取为 ∆t/10.
1.6 算法并行化实现
本文采用区域分解策略,基于消息传递接口MPI 实现虚拟区域方法的并行编程.本文作者Lin 等[37]已经实现了针对牛顿流体的并行虚拟区域方法.在此基础上,需要对黏弹性流体本构方程的求解并行化处理.其难点在于对流项的高精度离散格式,每个子区域需要两层或者更多的额外单元,用于存储其他子区域交换过来的网格信息.
如图1 所示,以二维计算区域为例,蓝色部分代表当前进程‘管理’的子区域,由于离散格式的要求,需要获得边界附近区域红色以及绿色部分的网格信息,例如流体速度和构型张量.本文采用以下策略实现该过程: (1)在区域“1”的基础上,通过数据交换先获得红色区域的网格信息;(2)在区域“2”的基础上,重复(1) 步骤获得绿色区域的网格信息.以此类推,通过重复(1)步骤可以获得更多层以上的网格信息,从而满足离散格式的需求.更多细节请参考文献[37].
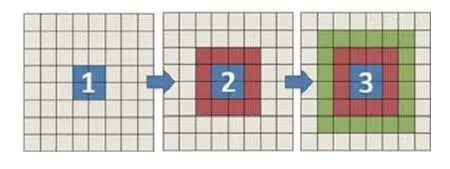
图1 网格信息交换示意图Fig.1 Schematic of data exchange
最后,如图2 所示,给出针对黏弹性流体的并行虚拟区域方法的算法流程图.
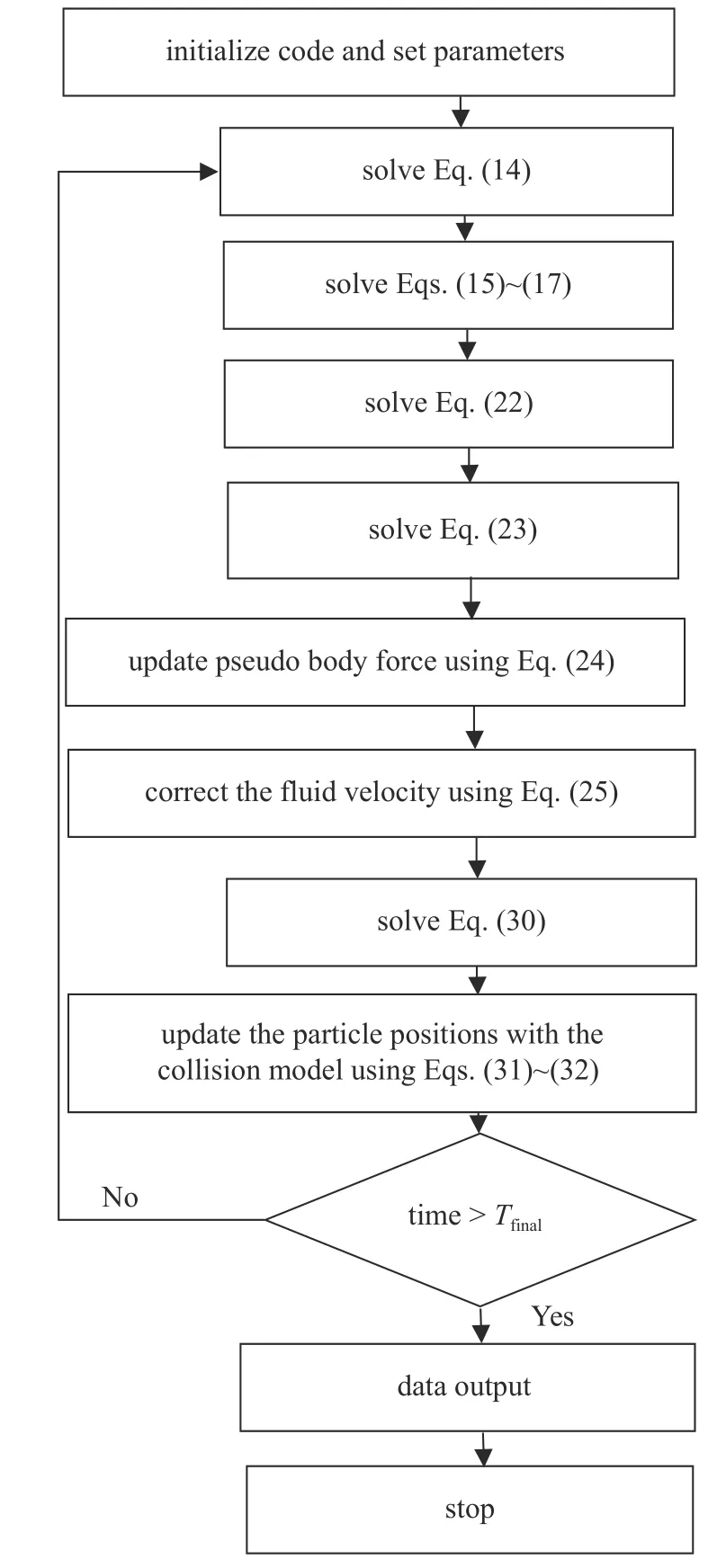
图2 并行虚拟区域法流程图Fig.2 Flowchart for the parallel fictitious domain method
2 算法验证
针对牛顿流体的并行虚拟区域方法在文献中已有大量的验证[33,37-40].在此基础上,进行本文算法精度验证.选取文献[14,41]的结果进行对比,按照文献选取工况参数如下: Reynolds 数Re=0.01;模型参数 α=0.2,µr=0.5,We=0 ∼4;粒子类 型β=5,−5,假定微生物颗粒与流体密度接近,即 ρr=1.0.计算区域大小为16 × 16 × 16,网格规模256 × 256 × 256,网格步长h=1/16,典型时间步长为 ∆t=0.000 5 ∼0.002.计算区域三个方向均设置为周期性边界条件.
如图3 所示,微生物颗粒自由游动,充分发展后两种类型粒子的平均速度UGK与文献[14,41]的结果吻合,验证了本文算法精度的可靠性.在此基础上,进行网格收敛性分析.图3(b)插图给出粗细两种不同网格下粒子游动速度随时间变化的计算结果,两者吻合较好,验证了网格收敛性.以下研究所有工况均采用网格步长h=1/16.

图3 两种类型粒子游动平均速度 UGK 随 W e 变化规律: (a) β=5,(b) β=−5.(b)插图为 β=−5,We=2 工况下粒子游动速度 U 随时间的变化曲线;黑色实线为粗网格 h=1/16,∆t=0.000 5 计算结果,红色实线为细网格 h=1/32,∆t=0.000 25 计算结果Fig.3 The average swimming speed UGK of squirmers: (a) β=5,(b) β=−5.Inset: squirmer swimming speed computed when using two different meshes at β=−5,We=2 ;black solid line represents the result of coarse grid h=1/16,∆t=0.000 5,and the red represents the result of fine grid h=1/32,∆t=0.000 25
3 结果与分析
本节将主要考察微生物在黏弹性流体中游动的壁面效应,重点探索近壁处微生物的行为特征以及相关的水动力机理,以期能够初步得到微生物在复杂流体中游动的变化规律.
微生物游动问题属于低Reynolds 数范畴,因此本节研究设定Re=0.01.在此基础上,着重研究流体弹性性质对微生物行为的影响规律,选取典型的Weissenberg 数范围We=0 ∼4.微生物模型选取两种典型粒子 β=3,−3.其他参数如下: α=0.2,µr=0.5,ρr=1.0;计算区域大小为 [ 0,16]×[0,16]×[0,16],网格步长h=1/16,典型时间步长为 ∆t=0.000 5 ∼0.001.计算区域方向y为壁面无滑移边界条件,其余两个方向均为周期性边界条件.粒子初始状态如图4 所示,初始位置位于z=0平面,粒子质心与壁面初始距离d=2,初始游动方向与x轴夹角 γ=−π/4.
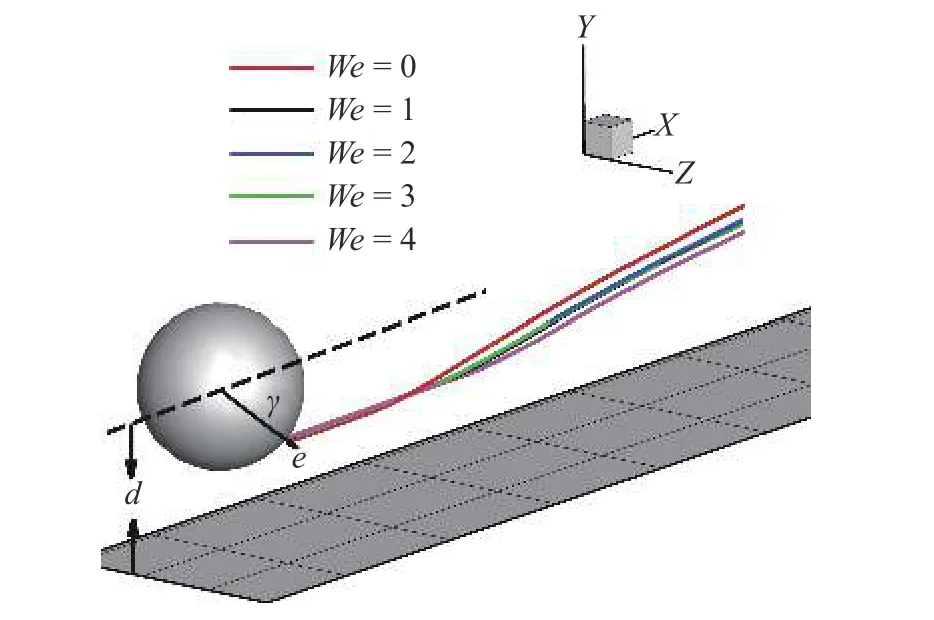
图4 微生物颗粒(β=3)与壁面作用轨迹图,粒子与壁面初始距离d=2,游动方向与 x 轴夹角 γ=−π/4Fig.4 Trajectory of puller (β=3) contact with wall,the initial distance between particles and wall d=2,the angle between swimming direction and x -axis γ=−π/4
首先,给出这两种类型粒子自由游动状态下周围的流场结构.工况参数如上,但计算区域三个方向均为周期性边界条件.如图5 所示,随体坐标系下,黏弹性流体(We=4)中两种类型粒子周围流场结构与牛顿流体(We=0) 类似.拉动型粒子(β=3)在尾部出现回流区,推动型粒子( β=−3)则出现在头部.与牛顿流体相比,黏弹性流体中流场速度较小,这与文献[14,41]结论一致.背景云图表示构型张量的迹 T r(C)=c11+c22+c33.如图5(b)所示,其极大值区域出现在推动型粒子尾部,表明该种粒子对尾部区域流体有很强的剪切作用.而拉动型粒子则是对粒子中部两侧区域有较强的剪切作用.
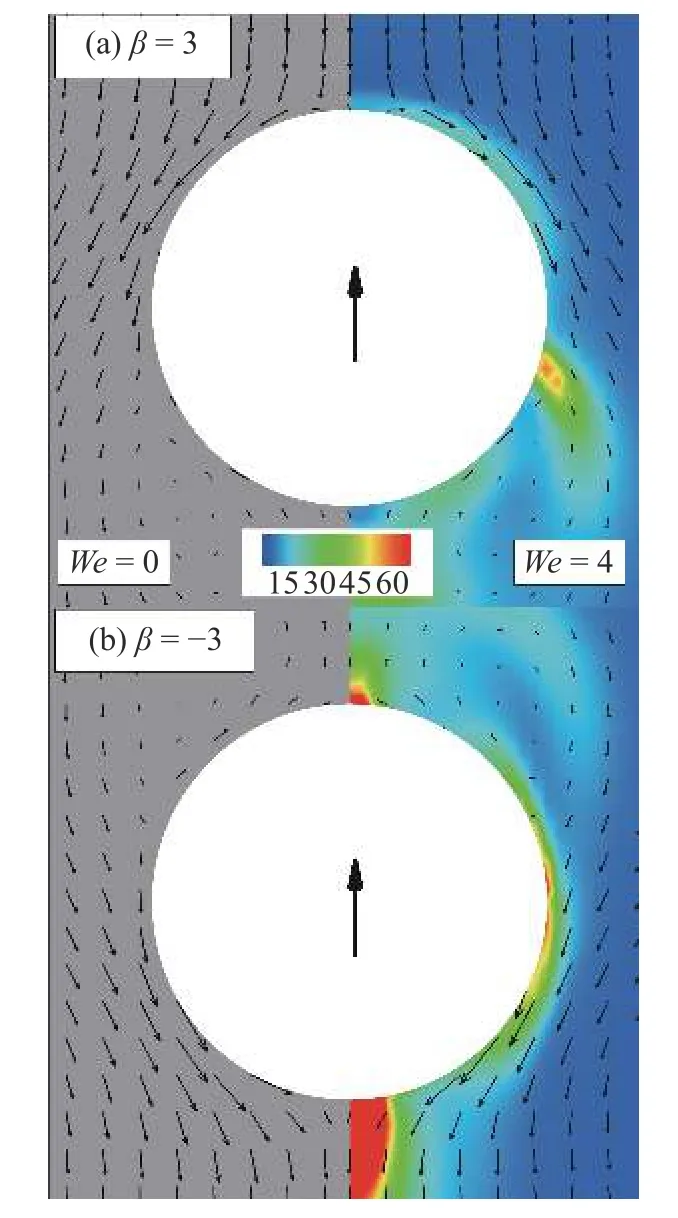
图5 微生物颗粒自由游动流场结构图.坐标系为随体坐标;黑色箭头表示颗粒游动方向,背景云图表示构型张量的迹 T r(C).左半部分图为 W e=0 结果;右半部分图为 W e=4 结果Fig.5 Flow field around squirmer particles free swimming in viscoelastic fluids with comoving frame;the black arrow represents the swimming direction of particles,and the background cloud chart represents the trace of the configuration tensor T r(C).The left part of figure shows the result at W e=0 ;the right part shows the result at We=4
在此基础上,研究黏弹性流体中微生物游动的壁面效应.图6(a)~图6(b)给出了两种微生物颗粒与壁面间隔距离d随时间发展的结果.对于拉动型粒子,在牛顿流体中,粒子与壁面充分接触之后逃离壁面.在黏弹性流体中,则有所不同.随着流体弹性增强,当We>2时拉动型粒子被壁面吸引,在壁面附近运动并与壁面保持一定的间隔距离,其轨迹如图4 所示.而对于推动型粒子,在两种流体中均逃离壁面.这里必须指出,上述结果与文献[14]的结论不尽相同.他们的结果表明随着流体弹性性质增强,微生物颗粒更容易被壁面吸引,这一点与本文结论一致.不同之处在于Re=0.1工况下,黏弹性流体中推动型粒子被困在壁面附近,而拉动型粒子则能够逃离壁面.可以认为这与流体惯性相关.文献[15]的结果表明,在幂律流体中流体惯性改变(Re=0.1 ∼0.5),导致推动型粒子在近壁处由被壁面吸引住转变为逃离壁面.Li 等[31-32]另外的研究工作指出牛顿流体中流体惯性影响微生物的行为特征.他们的结果表明,随着Reynolds 数的增加(Re=0.1 ∼1.0),微生物可以在逃离壁面和困在壁面两种状态转换[32];甚至在Re=50工况下,微生物颗粒的游动出现不稳定性,呈现复杂的三维行为特征[31].这些结果表明流体惯性对微生物的运动特性具有复杂影响;需要进一步研究.最后给出微生物颗粒与壁面的接触时间,接触判断标准为d 图6 不同类型微生物颗粒与壁面间隔距离 d 随时间变化曲线.黏弹性流体的参数为: R e=0.01,W e=0 ∼4,α=0.2,µ r=0.5,ρr=1.0Fig.6 The distance between squirmer particles and the wall in the y direction as a function of time.Parameters of viscoelastic fluid:Re=0.01,W e=0 ∼4,α=0.2,µ r=0.5,ρr=1.0 对于上述现象,可以认为与微生物颗粒的游动方向有关.图7 给出粒子游动方向与x轴的夹角随时间发展的结果.在牛顿流体中,经过与壁面接触之后,拉动型粒子游动方向调整为与x轴几乎平行.而在黏弹性流体中,其方向则明显倾向壁面,因此粒子保持向壁面游动,无法逃离壁面.对于推动型粒子,如图7(b)所示,夹角 γ由初始角度 − π/4 发展为接近 π/8,表明粒子的游动方向由倾向壁面发展为远离壁面,与其行为特征吻合. 图7 微生物颗粒游动方向与 x 轴夹角随时间变化曲线.黏弹性流体的参数为: R e=0.01,W e=0 ∼4,α=0.2,µ r=0.5,ρr=1.0Fig.7 Angle between squirmer particles swimming direction and the x -axis as a function of time.Parameters of the viscoelastic fluid:Re=0.01,W e=0 ∼4,α=0.2,µ r=0.5,ρr=1.0 为了进一步探讨其背后的水动力机理,可以对微生物颗粒进行动力学分析.图8 给出粒子在x−y平面内受到的水动力转矩Tz;图9 给出粒子受到的壁面垂直方向水动力Fy.两者计算公式如下 图8 微生物颗粒在 x −y 平面内受到的水动力转矩 T z 随时间变化曲线.其中,T v,z 表示黏性转矩 z 方向分量,T e,z 表示弹性转矩 z 方向分量,计算公式见式(33).黏弹性流体的参数为: R e=0.01,W e=0,4,α=0.2,µ r=0.5,ρr=1.0Fig.8 Hydrodynamic torque in the z direction computed using Eq.(33).Tv,z represents the viscous torque and T e,z the elastic torque.Parameters of the viscoelastic fluid: R e=0.01,W e=0,4,α=0.2,µ r=0.5,ρ r=1.0 这里选取We=0,4两种典型的工况进行分析.由图8(a)可以看出,近壁处,黏性应力产生的转矩Tv,z>0,呈现逆时针方向,促使拉动型粒子游动方向远离壁面;而弹性应力则相反,转矩Te,z<0,呈现顺时针方向,促使粒子游动方向倾向壁面.对于推动型粒子,如图8(b)所示,黏性应力产生更大的转矩,使得粒子游动方向远离壁面,从而导致粒子能够逃离壁面.这表明游动方向是影响微生物颗粒壁面效应的重要因素.弹性应力对游动方向的调制作用是黏弹性流体中微生物被壁面吸引的重要机理. 图9 给出微生物颗粒受到的壁面垂直方向水动力.在壁面附近区域,黏性应力Fv,y<0,对微生物颗粒呈现吸引作用,促使粒子向壁面运动;而弹性应力Fe,y>0,呈现排斥作用,促使粒子远离壁面.随着时间发展,如图9(b)所示,推动型粒子受到的黏性应力变排斥作用;而弹性应力则变为吸引作用.这个转变过程与推动型粒子游动方向由倾向壁面(γ <0)转变为远离壁面(γ >0)相吻合,我们认为与此有关. 图9 微生物颗粒在壁面方向受到的水动力 F y 随时间变化曲线.其中,F v,y 表示黏性应力 y 方向分量,F e,y 表示弹性应力 y 方向分量,计算公式见式(33).黏弹性流体的参数为: R e=0.01,W e=0,4,α=0.2,µ r=0.5,ρr=1.0Fig.9 Hydrodynamic forces in the y direction computed using Eq.(33).Fv,y represents the viscous force and F e,y the elastic force.Parameters of viscoelastic fluid: R e=0.01,W e=0,4,α=0.2,µ r=0.5,ρr=1.0 本文采用基于虚拟区域法,结合乔列斯基分解的数值方法,研究黏弹性流体中微生物游动问题.对于黏弹性流体本构方程的求解: (1)构型张量采用乔列斯基分解为一个上三角矩阵与一个下三角矩阵的乘积,并对对角线元素采用指数函数替换,从而在理论以及计算方面保证构型张量的对称正定性质;(2)对流项采用高精度的MUSCL 格式离散;(3)本构方程采用显式求解,时间积分采用四阶龙格库塔方法. 本文将上述方法初步应用于研究微生物游动中的壁面效应.结果表明,游动方向是影响微生物颗粒壁面效应的重要因素.弹性应力对游动方向的调制作用是黏弹性流体中微生物被壁面吸引的重要机理.我们发现: (1)对于拉动型微生物颗粒,Weissenberg数较大的工况下(We>2),流体弹性应力产生一个反向转矩,使得其游动方向显著倾向壁面,从而阻碍微生物逃离壁面;(2)两种类型粒子在黏弹性流体中与壁面作用时间较长,几乎达到牛顿流体的两倍以上;(3)近壁处,弹性应力对两种类型粒子呈现排斥作用,而黏性应力则呈现吸引作用. 未来将在本文基础上,进一步研究黏弹性流体中微生物与复杂界面的相互作用以及近壁处微生物的行为特征,尝试揭示其中的动力学机理以及变化规律,为微型器件的设计制造提供理论指导. 数据可用性声明 支撑本研究的科学数据已在中国科学院科学数据银行ScienceDB 平台公开发布,访问地址为https://www.doi.org/10.57760/sciencedb.j00140.00009.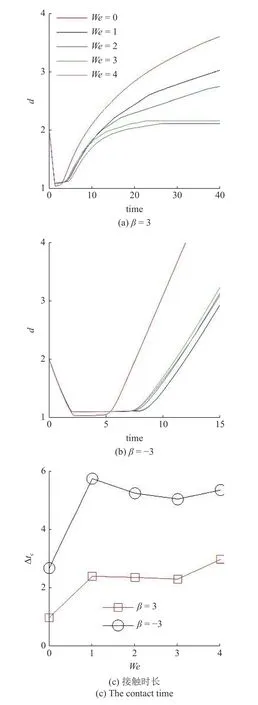
4 结论

