双振子同异步振动主动控制湍流边界层减阻实验研究1)
白建侠 赵凯芳 程肖岐 姜 楠 ,,2)
* (天津仁爱学院数学教学部,天津 301636)
† (天津大学机械工程学院力学系,天津 300354)
** (天津市现代工程力学重点实验室,天津 300354)
引言
壁面摩擦阻力是湍流边界层阻力的主要来源.在湍流边界层中,不同区域的相干结构的类型不同,在湍流边界层的黏性底层和缓冲层中最主要的相干结构为高、低速条带结构及准流向涡结构,对数律区的相干结构主要为发卡涡和发卡涡包结构,外区则存在着超大尺度结构[1-4].相干结构是壁湍流脉动的关键机制,通过有效控制相干结构来减小壁面摩擦阻力是湍流边界层减阻的关键所在.
湍流边界层中存在着大小不同尺度的结构.Adrian等[5-8]发现了大尺度瞬态结构,通过提取其统计特征,提出了发卡涡和发卡涡包模型.Hutchins 等[9-10]发现湍流边界层的超大尺度结构和大尺度结构对小尺度结构有调幅作用,并预测了近壁区的统计特性.Tang 等[11]的分析结果表明,当选取截止波长为2 倍边界层厚度左右时,大尺度和小尺度结构之间具有良好的鲁棒性.
条带结构和准流向涡结构之间有非常紧密的关系.条带结构的流向长度超过 1 000δv,其中 δv=ν/uτ为特征长度,ν表示运动黏性系数,uτ表示壁面摩擦速度.条带结构是由低速流体沿流向拉长而形成,这些结构在展向上呈周期性分布,条带之间平均间距约为 8 0δ ∼120δ,高速流体分布在两个低速条带结构之间,准流向涡结构分布在条带结构侧面,其直径约为 3 0δ[12-13].
Hamilton 等[14]发现近壁区相干结构的周期性循环再生过程可分为三部分: 在准流向涡诱导作用下产生条带结构;条带结构失稳破碎;准流向涡重新生成.对湍流边界层近壁区条带结构和准流向涡构成自维持过程中的任何一个环节进行控制,都能实现对湍流的抑制作用,减小壁面摩擦阻力[15-19].
湍流边界层减阻控制根据是否需要外加的能量消耗分为被动控制和主动控制[20-22]两大类.主动控制的优点是能适应流场流动状态的变化和相干结构的时空特性,是目前湍流边界层减阻控制研究的热点.主动控制通过动作器将控制电信号转换为对相干结构有针对性的扰动,来实现减阻.主动控制减阻包括电磁体力减阻、微气泡减阻、壁面振动减阻、抽吸扰动减阻及零质量射流减阻等.零质量射流又称合成射流,可实现对外输出动量但输出质量为零.不需要额外的流体质量供给,控制系统小巧灵活,安装在固壁表面非常方便,具有其独特的优势作用.
零质量射流激励器的振动方式有活塞式、压电薄膜式、电磁激励式等[23].Guo 等[24]通过高频零质量射流的方式实现湍流边界层中减阻.罗振兵等[25]提出拥有两个腔体的双合成射流,推进了激励器的结构发展和适用范围.Park 等[26]采用PIV 进行实验研究,发现不同振动频率和入射角的合成射流对湍流边界层产生影响,并发现了大尺度的展向涡结构.Ye 等[27]用合成射流阵列进行主动控制,发现合成射流阵列的作用主要集中在对数区域,并可显著改变湍流边界层的流场结构.Lu 等[28]采用圆形的合成射流阵列实现了主动控制湍流边界层.Wang 等[29]通过圆柱绕流实验验证了Zhang 等[30]提出的高效零质量射流激励信号.
动作器是主动控制实验中的核心器件,它直接与流场接触,通过电能实现流场扰动.Cattafesta等[31]将动作器分为三类: 流体动作器、电磁动作器以及固体动作器.固体动作器有操作方便且易于实现控制的优点.常见的固体动作器有壁面振荡和压电陶瓷(piezoelectric,PZT)振子.压电陶瓷材料的抗电磁干扰能力很强,PZT 振子在交流电压驱动下可以较小的能量输入实现对流场较大的扰动,从而实现对流场的高效控制.
Jung 等[32]通过高频的壁面展向振荡方式,通过DNS 方法实现了对湍流边界层相干结构的主动控制,得到最大40%的减阻效果.Stoke [33]研究了壁面空间振荡的减阻效果,并对比分析了不同的振荡幅值对减阻效果产生的影响.Choi[34]采用等离子体激发器实现对湍流边界层主动控制,得到45%的减阻率.Jacobson 等[35]首次将PZT 振子应用在流动控制中,发现振子振动会诱导出一对反向旋转涡和高低速条带结构.Bai 等[36-37]用PZT 振子阵列方式对湍流边界层实施壁面扰动,发现扰动产生了新的流向涡结构,并获得显著的减阻效果.Qiao 等[38]用PZT振子采用闭环策略,发现扰动抑制了近壁高速流体事件,减小了壁面摩擦阻力,得到最大减阻率为23%.Zheng 等[39-42]利用压电陶瓷PZT 振子对流场进行扰动,得到了较好的减阻效果.
本文采用热线测速技术,以展向双压电陶瓷PZT 振子为动作器,自主设计了零质量射流主动控制湍流边界层减阻的实验装置,在风洞中开展了双压电振子同步和异步振动主动控制湍流边界层减阻的实验研究.通过对湍流脉动速度信号进行多尺度特征分析,比较不同工况下双PZT 振子的同步和异步控制对大尺度和小尺度相干结构的调制作用,并分析PZT 振子下游流向位置的变化对湍流边界层的影响.
1 实验装置
本文实验在天津大学流体力学实验室的三元低速回流式风洞中进行,开展了不同工况的零质量射流PZT 振子主动控制实验研究.风洞实验段尺寸长为1500 mm,宽800 mm,高600 mm,横截面是切角的矩形.实验平板由有机玻璃材料制作,其尺寸为1700 mm × 600 mm × 15 mm,竖直放置在风洞实验段的中心线处.为了加速边界层转捩,在平板前缘下游80 mm 处安装了直径为2 mm 的绊线及四块砂纸,以保证实施控制和进行热线测量的边界层达到充分发展的湍流边界层.
以镶嵌在平板上展向对放的两个PZT 振子为主动控制激励器,实现对壁湍流的周期扰动.实验中使用的PZT 振子由压电陶瓷片和铜片粘结而成,上表面为铜材料,下表面为压电陶瓷材料,其尺寸根据材料的特性来确定.实验中选取的压电陶瓷片宽3.6 mm、厚0.22 mm,铜片宽3.6 mm、厚0.2 mm,振子的有效振动长度为30 mm.本文中PZT 振子的力学参数如表1 所示,其中E为弹性模量,ρ′为材料密度,µ为泊松比.

表1 PZT 振子材料主要力学参数Table 1 Main material property of PZT actuator
在距离前缘1090 mm 的中心线处,实验平板上实施控制和测量的位置切割出了一块长150 mm、宽100 mm 的凹槽,如图1 所示.两个PZT 振子沿展向对放布置,以悬臂梁的形式平行悬挂在深度为5 mm 的空腔上(图2 和图3),并嵌入到实验平板的凹槽中.
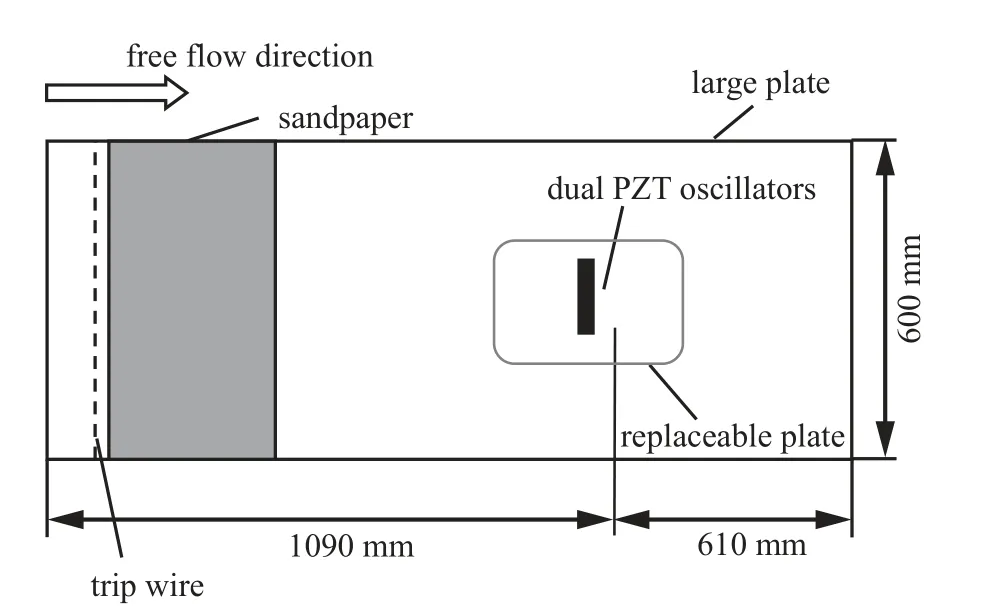
图1 实验平板示意图Fig.1 Sketch map of flat plate

图2 双PZT 振子实物图Fig.2 Picture of dual PZT vibrators

图3 PZT 振子悬臂梁模型示意图Fig.3 Cantilever beam model of PZT oscillators
如果把两个PZT 振子的铜片极均与电源同一极相连,陶瓷片极都与电源另一极相连,PZT 振子作同向振动,即为同步控制的工况(syn);若将一个PZT 振子的铜片与另一个PZT 振子的陶瓷片连到电源的一极,则为异步振动的工况(asyn).计算得到PZT 振子的一阶固有频率为254 Hz,本文中实验选取的驱动频率均小于254 Hz.
对PZT 振子进行谐响应分析,可以得到系统的动态响应.根据频率响应函数,计算出各控制工况下振子自由端的位移A与施加的电压幅值成正比,振子振幅在0.1 mm 量级,具体数据如表2 所示.PZT振动造成的外部流场扰动,主要集中在垂向6 mm 以内,远大于振子的振动振幅.
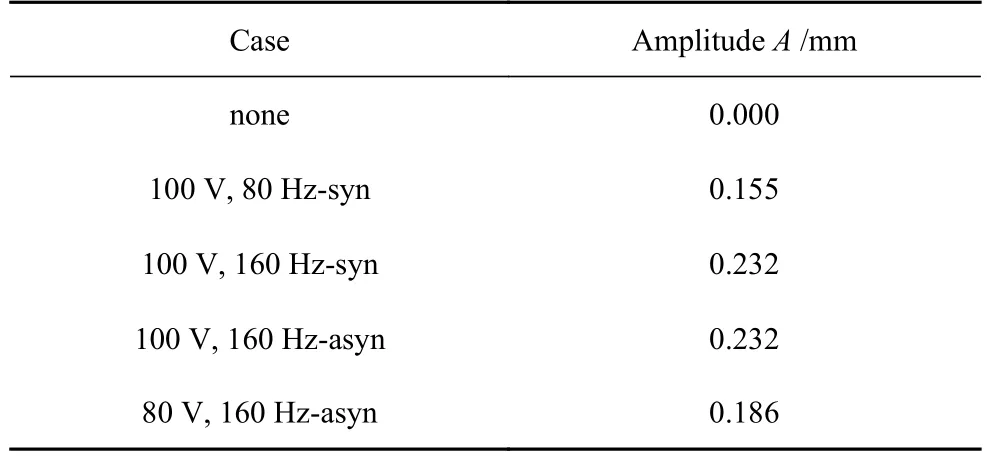
表2 不同工况振子振幅Table 2 Amplitude of oscillator in different case
实验采用热线测速HWA 技术,使用由美国TSI 公司生产的TSI-IFA300 型恒温热线风速仪进行热线测量,用TSI-1621 A-T1.5 型单丝湍流边界层热线探针采集速度信号.用支杆将热线探针固定在CCTS-1193 E 型三维自动控制坐标架上,通过计算机操作实现在流向、展向及法向三个方向控制探针的精确移动和定位.为PZT 振子输入电压幅值和振动频率的是远方GK10005 交流变频稳压电源.风洞实验段的自由来流速度选取为U∞=9.2 m/s, 边界层名义厚度(速度达到主流区速度的 0.99U∞处到壁面的垂直距离) 为 δ=43.05 mm,动量损失厚度θ=4.51 mm,动量损失雷诺数Reθ=2766,其中θ=∫U(1−U/U∞)/U∞dy,U为流向平均速度,Reθ=θU∞/ν,ν为运动黏性系数.热线探针在PZT 振子下游处布置,实现对湍流边界层不同法向位置的流向脉动速度信号的精确测量.采样频率设定为100 kHz,每个空间点样本总量为4194304 个,采样时间为41.9 s.
首先在PZT 振子下游2 mm 处进行了无控制工况和不同电压幅值和振动频率的同步和异步控制测量实验.实验中选取PZT 振子输入的电压幅值为100 V 和80 V,振动频率为80 Hz,160 Hz,240 Hz.为了进一步观察压电振子的振动对下游不同流向位置产生的影响,在压电振子下游2 mm,4 mm,6 mm 处又进行了不同的实验工况测量.
2 实验结果分析
2.1 平均速度剖面
图4 给出了施加控制工况与无控制工况下由黏性内尺度单位无量纲化的湍流边界层的平均速度剖面的对比图,其中u+=u/uτ,y+=yuτ/ν分别表示由壁面摩擦速度和运动黏性系数无量纲化的流向平均速度和法向位置.图4(a)为相同电压(100 V)下三个不同振动频率(80 Hz,160 Hz,240 Hz)对应同步控制工况的平均速度剖面与无控制工况(none)的对比;图4(b)为相同电压和频率(100 V,160 Hz)下对应的同步和异步工况与无控制工况(none)的对比.其中红色、蓝色和绿色线对应不同施加控制工况,黑色线对应无控制工况.
图4 中可以看出,与无控制工况相比,所有施加控制工况的平均速度剖面对数律区起始的横坐标均出现远离壁面的特征,对数律区的抬升现象意味着壁面摩擦阻力减弱,也说明施加控制后有明显的减阻效果.

图4 不同工况平板湍流边界层平均速度剖面Fig.4 Average velocity profiles of the turbulent boundary layer
图4(a)中可以看出,在相同电压三种不同频率下,频率为160 Hz 的控制工况的对数律区抬升最多,说明频率为160 Hz 时减阻效果最好.图4(b)中,同电压同频率下异步控制与同步控制的工况相比,对数律区上移要明显,说明异步控制比同步控制减阻效果好.
2.2 减阻率
根据平板湍流边界层的对数律平均速度剖面
壁面摩擦系数和减阻率可通过以下公式得到
其中,ρ为空气密度,Cf为控制工况的壁面摩擦系数,Cf0为无控制工况的壁面摩擦系数,η为减阻率.经过计算得到不同工况的减阻率 η如表3 所示.

表3 不同工况减阻率Table 3 Drag reduction rate for each case
由表3 可知,所有控制工况中,异步控制工况100 V,160 Hz 时得到最大减阻率为18.54%.在同一电压幅值三种不同的振动频率中,振动频率为160 Hz 时减阻效果最佳.在相同电压和频率下,异步控制比同步控制的减阻效果要好.
下面用小波分析、条件平均等方法对湍流边界层流向脉动速度信号数据进行多尺度分解,发现PZT 振子的同步和异步振动产生了对湍流边界层多尺度相干结构的调制作用,调整了近壁区的含能分布.
2.3 小波系数概率密度函数
本文采用小波分析方法对实验得到的时间序列信号进行时频局部化处理.小波分析是将时间序列信号u(t)与一个被称为小波函数的解析函数在b时刻的局部窗口内进行卷积
小波系数Wu(a,b) 相当于对信号u(t)在自适应时间窗内进行局部时间段内的带通滤波,实现由粗到细一层层解剖信号.对速度信号进行小波变换后,可得到不同尺度涡结构的细节信息.当尺度a较小时,代表信号中的高频小尺度成分.当尺度a较大时,代表信号中的低频大尺度成分.在小波分解的所有尺度中,一定存在一个占有湍流脉动动能最多的能量最大尺度a∗.湍流相干结构所对应的时间尺度可由小波分解的能量最大准则确定[43].当提取多尺度相干结构后,无控制工况的概率密度函数在各个法向位置均与高斯分布趋于一致,呈现出对称性的特点.小波系数概率密度函数形状与高斯正态分布曲线的符合程度代表了间歇性的强弱,可以反映出不同尺度相干结构与湍流间歇性的关系[44].
图5 给出了近壁区四个不同法向位置y +=11,y +=15,y +=21,y +=30 处流向脉动速度第九尺度(无控制工况的能量最大尺度)小波系数Wu(a,b)的概率密度函数分布(probability density functions,PDF)对比曲线.图5 中可以看出,不施加控制的工况的湍流脉动有一定的随机性、无序性和不规则性,80 Hz 的两种控制工况概率密度函数曲线的变化,说明湍流间歇性减弱.

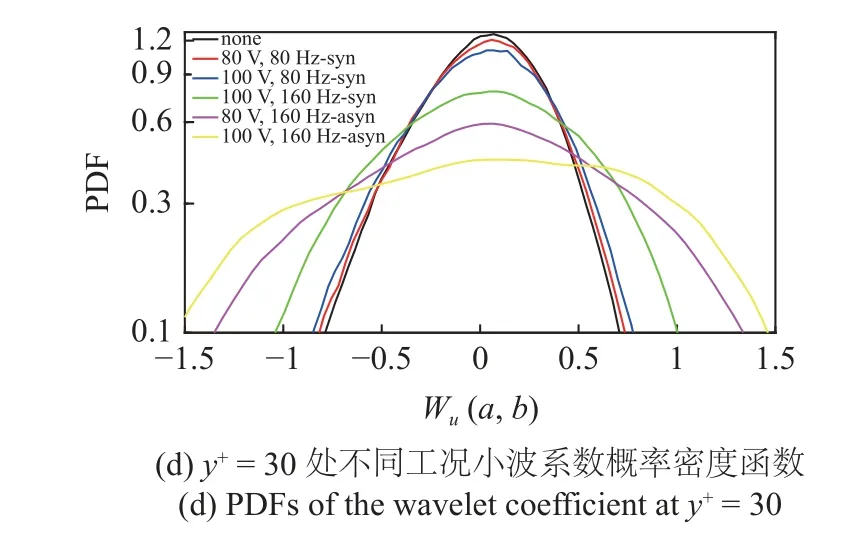
图5 不同法向位置小波系数概率密度函数Fig.5 PDFs of the wavelet coefficient Wu (a,b) at different normal positions
在施加控制160 Hz 的三种工况中,概率密度曲线呈现出明显的波动特征,小波系数幅值在0 附近的概率减小,小波系数概率密度函数图像尾部均呈现变宽的趋势,说明PZT 的周期扰动产生了新的湍流结构,湍流随机脉动受到抑制作用,使得湍流边界层近壁区的湍流脉动更加有序和规则[45],有很好的控制效果.
2.4 能量尺度分布三维图
将小波系数Wu(a,b)的平方对时间积分,得到速度信号u(t) 的不同尺度a所对应的能量表示如下
其中W(ω) 是小波母函数W(t)的傅里叶变换.
图6 为不同工况不同法向位置的湍流脉动动能E(a)随尺度的变化曲线,其中横轴代表不同小波尺度a,纵轴表示不同尺度对应的能量E(a).选取了近壁区五个不同的法向位置进行分析.
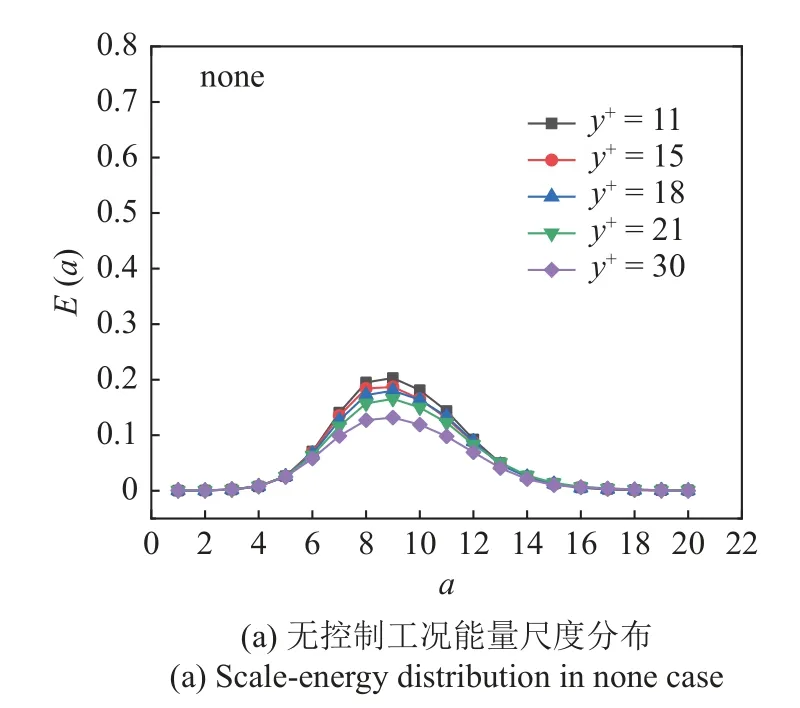
图6 不同法向位置能量随尺度分布Fig.6 Scale-energy distribution at different normal positions

图6 不同法向位置能量随尺度分布(续)Fig.6 Scale-energy distribution at different normal positions (continued)
图6 可以看出,随着法向位置逐渐远离壁面,不同工况中湍流脉动动能的最大峰值均呈现逐渐减小的趋势.其中异步100 V,160 Hz 振动工况能量峰值明显高于其他控制的工况.对压电振子施加周期扰动后,产生了对相干结构猝发的调制作用,出现了小尺度湍流脉动增加,大尺度湍流脉动减少的情况.
2.5 小尺度脉动条件相位平均
为了对湍流边界层中的相干结构进行多尺度分析,寻找一个合适的方法将大尺度脉动和小尺度脉动分离出来,进而研究PZT 振子的周期扰动对小尺度脉动产生的影响及小尺度脉动随时间的变化规律,文中采用低通滤波的方法进行分析.低通滤波就是通过特定的截断频率(波长)将流场信号进行分解.
文献[10-11,46-47]相关研究表明,当截止波长选取 λ/δ=2时,对大小尺度相干结构及其相互关系的分析结果都有很好的鲁棒性.因此,本文选取λ/δ=2为截止频率,其中 λ=2π/k为波长,k为波数,δ为边界层名义厚度.
对流向脉动速度信号以 λ/δ=2为截止频率低通滤波后得到大尺度脉动 (uL) 和小尺度脉动 (uS).接下来将大尺度脉动uL+=0附近的小尺度脉动进行了条件平均
图7 为不同工况下对小尺度脉动条件平均的云图,不同颜色代表对应不同的能量幅值.选取了同步100 V,160 Hz 工况(图7(c)和图7(d))和无控制工况(图7(a)和图7(b))进行比较分析.
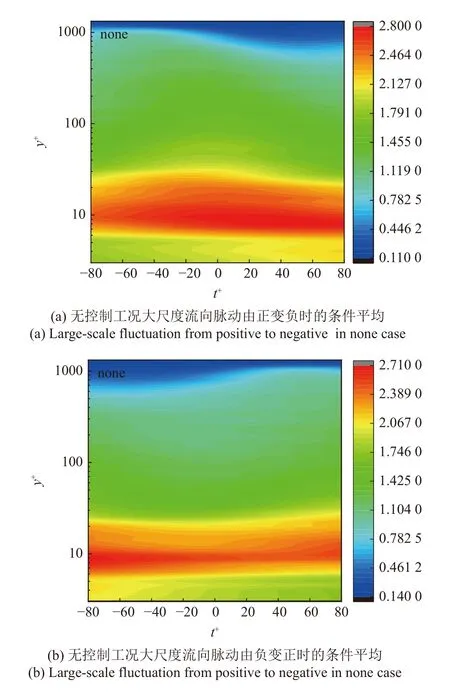
图7 小尺度振幅的条件平均Fig.7 Conditional averaging of small-scale fluctuations amplitude

图7 小尺度振幅的条件平均(续)Fig.7 Conditional averaging of small-scale fluctuations amplitude (continued)
图7 可以看出,在同步100 V,160 Hz 控制工况中,PZT 振子的周期性扰动使得近壁区小尺度脉动的幅值明显增强;而扰动对外区小尺度脉动幅值影响不大.同时,施加控制后发现小尺度脉动的增强范围主要集中在大尺度脉动为正值的时间中,而大尺度脉动为负值的时间中增强不明显.这可解释为双PZT 振子对湍流边界层近壁区施加周期扰动后,引起了对大尺度脉动为正值时的高速流体扫掠事件的影响,抑制了高速流体下扫时壁面摩阻产生的主要过程,使大尺度结构破碎成小尺度结构,从而增强了小尺度脉动的强度,减小了壁面摩擦阻力,实现减阻.
2.6 不同流向位置能量尺度分布
上述工况的相关分析均选取的是PZT 振子下游2 mm 处,为了对PZT 振子振动对湍流边界层下游不同流向位置的影响进行研究,分别采集了振子流向下游三个不同的流向位置2 mm,4 mm,6 mm处的流向脉动速度信号,对100 V,160 Hz 异步控制工况和无控制工况进行对比.
图8 给出了100 V,160 Hz 异步振动工况与无控制工况的能量尺度分布云图,横轴表示小波分解的尺度a,纵轴为无量纲化的法向位置y+,不同颜色表示不同的能量幅值.图8 可以看出,在PZT 振子下游位置2 mm 及4 mm 处,控制工况的能量幅值均较无控制时增加明显,能量更加集中于y+=10附近.

图8 不同流向位置 100 V,160 Hz-asyn 工况多尺度流动能量分布Fig.8 Energy cloud distribution of the multi-scale flow structures for 100 V,160 Hz-asyn case at different streamwise positions

图8 不同流向位置 100 V,160 Hz-asyn 工况多尺度流动能量分布(续)Fig.8 Energy cloud distribution of the multi-scale flow structures for 100 V,160 Hz-asyn case at different streamwise positions (continued)
但随着流向位置逐渐远离PZT 振子下游,振子的周期性扰动对于湍流边界层的调制作用逐渐减弱.在压电振子下游6 mm 处,施加控制后的能量尺度分布和无控制时已经非常接近,说明在该流向位置处PZT 振子的振动对湍流边界层的影响变得很小.说明双PZT 振子的周期性扰动对湍流边界层的减阻沿流向方向逐渐衰减.
3 结论
本文自主设计了一套PZT 振子为激励器的零质量射流主动控制实验装置,并分析研究了双PZT振子的同步及异步振动对湍流边界层多尺度相干结构的影响,得出以下几个结论.
(1) 异步控制工况100 V,160 Hz 时得到最大减阻率为18.54%.同电压频率为160 Hz 时减阻效果最优.同电压同频率下,异步控制比同步控制的减阻效果要好.控制后小尺度能量增加,大尺度能量减少.
(2) 施加控制160 Hz 的三种工况中曲线呈现出明显的波动特征,说明受振子周期扰动作用,近壁湍流脉动更加有序和规则,湍流间歇性减弱,控制效果较好.
(3) PZT 振子的异步振动对相干结构猝发的调制作用显著增强,PZT 振子的扰动增强了小尺度脉动强度,将大尺度破碎成小尺度结构.
(4) 随着流向位置逐渐远离PZT 振子,振子的周期性扰动对湍流边界层的调制作用逐渐减弱.

