改进算法在导弹结构热防护一体化中优化研究

齐名军 , 王志宝, 吴 凯, 邓 红, 谷海红

(1. 鹤壁职业技术学院, 河南 鹤壁 458030; 2. 东北石油大学, 黑龙江 大庆 163318; 3. 天津农学院, 天津 300191; 4. 黑龙江工程学院, 哈尔滨 150050; 5. 河南理工大学, 河南 鹤壁 458030)

0 引 言

导弹进入地球大气层超高速飞行时, 其外部由摩擦产生的热量在300 ℃到1 500 ℃之间, 给结构抗变形能力及热防护体系带来极大的考验[1], 而结构热防护一体化技术的出现, 为导弹在大气层超高速飞行所面临的困境提供了新思路[2]。 结构热防护一体化技术的实质是将承载负荷和隔热双重功能集于一身的技术[3], 该技术还有较高的比强度、 比刚度及便于修理卸载等优点, 在各类高超声速飞行器中得到广泛应用[4]。 文献[5]把结构热防护一体化技术应用到航天器中, 并构建航天器一体化结构综合性能评价方法与体系。 文献[6]把该技术应用到超高速飞行导弹中, 实验表明该技术在承载和隔热两个方面具有良好的效果。 仿生学的出现加快新型承载/防热一体化结构的发展, 如莲藕结构等, 虽然双重功能良好但制造工艺较为困难[7]。 目前该技术在超高声速飞行器应用研究中的最大难点是在壁宽毫米量级超高速飞行器上难以实现[8], 原因在于随着导弹隔热层壁宽减小, 腹板热短路效应增强, 热防护功能失灵, 因此腹板镂空设计被淘汰。 文献[9]研究证实了波纹夹芯结构制造工艺相对简单, 未来应用优势明显。

随着群体智能优化算法的出现, 国内外学者为提高一体化结构性能, 把智能优化算法尝试性应用到该体系中。 文献[10]采用SA算法且仅从结构方面降低波纹夹芯一体化结构质量; 文献[11]利用GA算法仅从隔热功能改善波纹夹芯板热防护效率; 文献[7]利用GA算法改善兼顾承载/热防护结构一体化的性能, 效果一般。 对算法深入研究发现, 群体智能优化算法在诸多领域应用中取得很大成功, 尤其在低维函数应用表现较佳, 但在解决复杂高维函数优化方面存在如下缺点[12]: 算法在种群个体进化期间多样性差, 收敛速度慢且易陷入“早熟收敛”, 无法获得高精度解。 樽海鞘算法(Salp Swarm Algorithm, SSA)也属于群体智能算法, 同样具有上述不足。 本文针对该算法存在的不足, 做出以下改进: (1)引入Sobol 序列对初始种群进行均匀化处理, 保持种群多样性, 提升算法全局勘探能力; (2)使用动态权重调节机制策略, 提高算法收敛速度; (3)融合变异因子和反向解策略, 有利于算法跳出局部最优, 提高算法精度; (4)多用一个临时储备库可以从单目标理论上最佳解集合获得满足实际需要的Pareto最优解。 最后, 把改进算法应用到导弹波纹夹芯结构热防护一体化中的热防护效率、 结构质量等多目标优化函数中, 利用罚函数法把多目标函数转化为单目标最小化进行求解计算。

1 导弹结构热防护一体化数学模型

导弹在太空大气层超高声速飞行时, 气动热与气动力载荷都要考虑到, 以文献[7]为例, 如果导弹热防护目标为300 ℃, 其舱体模型大小如图1所示, 气动热载荷转化为温度载荷如图2所示, 且作用在结构外壁, 气动力载荷等效处理为1 000 N·m。 若实验模型无辐射, 结构内壁底部绝缘, 仿真将会推出一种理想的结论。

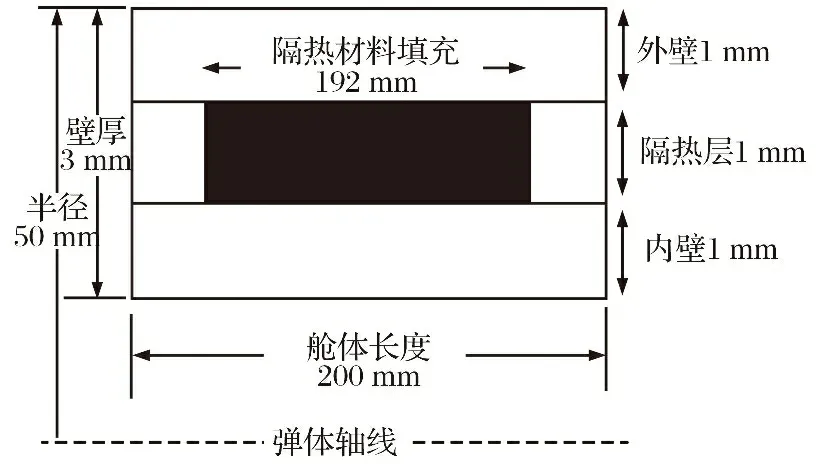
图1 导弹舱体模型Fig.1 Missile cabin model

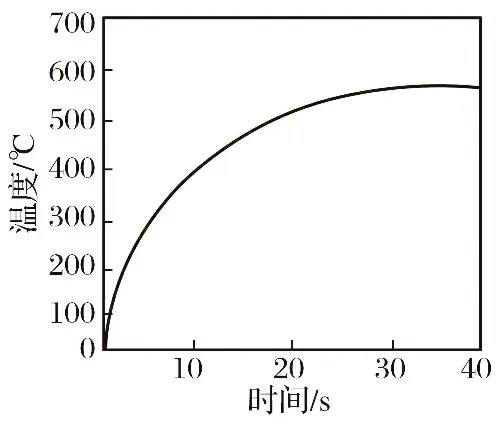
图2 温度载荷Fig.2 Temperature load

通过文献[7]中对导弹的热-结构耦合实验, 得到导弹舱体的温度分布, 如图3所示。 分析可知, 其温度分布呈“U型”轴对称状态, 随着位置的增加, 两端高温区逐渐对称地过渡到中部低温区, 位置在区间38～160 mm时温度保持不变, 距离舱体两端16 mm范围内, 内表面温度大于300 ℃。 为防止弹体损坏, 在两端位置安装连接环, 如图4所示。 此时, 范围总宽度增加, 热容增大, 使舱体内表温度下降。

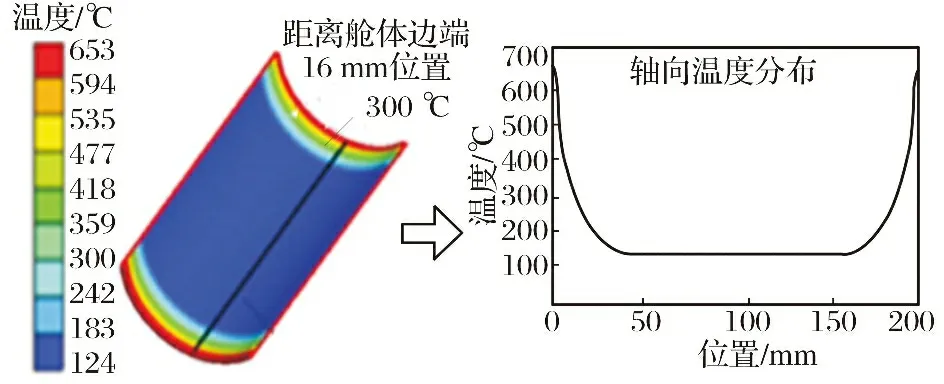
图3 温度分布Fig.3 Temperature distribution

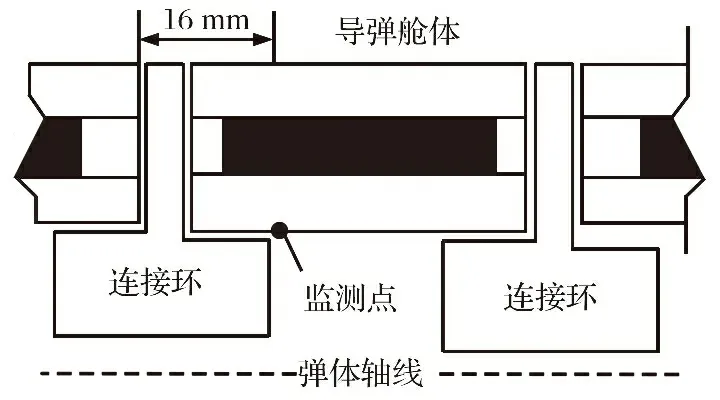
图4 舱体结构设计Fig.4 Cabin structure design

热-结构耦合分析的应力分布结果如图5所示。 由图5可知, 该结构真实分布特点反映出其具有较好的承载能力。 舱体中部应力强度大, 舱体结构极易发生破坏, 属于应力薄弱范围区域。 由文献[7] 可知, 通过热-结构仿真计算时, 对网格进行了收敛性检验, 所得到的距离舱体顶端16 mm的温度与结构最大应力如表1所示。 其中, 综合计算精度与效率, 网格尺度取0.1 mm。

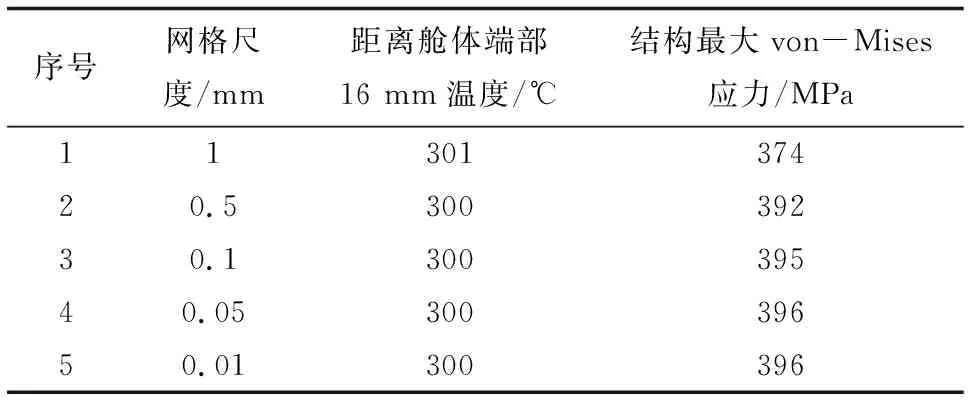
表1 温度与结构最大应力Table 1 Temperature and maximum structural stress

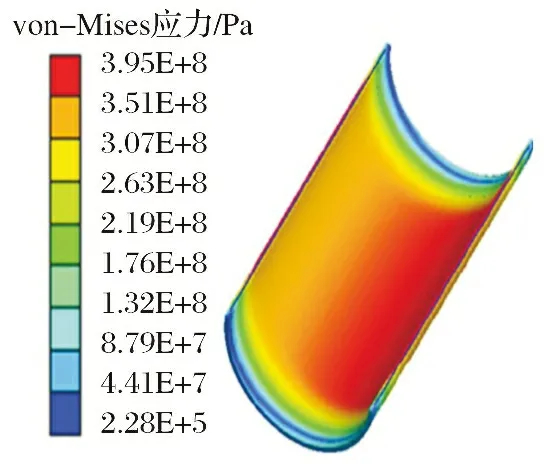
图5 应力云图Fig.5 Stress cloud

由表1可知, 距离舱体端部16 mm时, 温度越低越好, 并且导弹结构所对应的最大von-Mises应力越小越好, 这样才能达到热防护目标。

文献[7]研究了外壁、 内壁及隔热层宽度对热防护性能的影响, 得出如下结论: 外壁宽度对热防护性能作用较小, 扩大隔热层与内壁宽度确实能够增强结构热防护性能。 但局限于舱体壁宽大小约束, 隔热层与内壁宽度不能无限增大, 且外壁宽度会随之降低, 结构承载能力变弱而发生变形。 因此, 在导弹结构热防护一体化优化研究中, 既要考虑结构热防护性能, 又要考虑弹体结构轻质化。

由以上模型分析可知, 进行弹体优化时, 需要研讨的要点如下: (1)保证导弹壁宽为3 mm; (2)结构承载能力要强, 在兼顾力-热双重作用下, 优化后弹体结构应力不能超出材料极限承载力; (3)考虑目前工厂加工精确程度, 将导弹壁宽精确到千分位。 实验隔热层填充材料采用 SY1000, 其余结构部分均采用钛合金材料, 具体材料参数见文献[7]。

本文案例是多目标优化问题, 即以结构热防护效率最大和结构质量最小为最终求解目标, 具体定义如下:

miny={y1,y2}

(1)

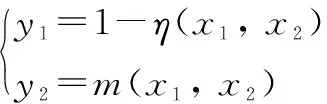
(2)

式中:x1为结构隔热层宽度;x2为结构内壁宽度;η(x1,x2)为结构热防护效率;m(x1,x2)为结构质量。

导弹一体化热防护结构的优化数学模型约束条件为

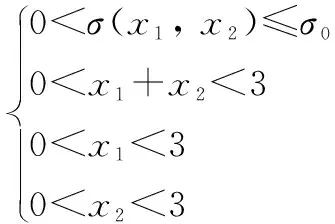
(3)

式中:σ(x1,x2)为结构最大应力。

本优化案例是多目标函数问题, 但考虑到以提高结构热防护效率优先, 采用单目标优化, 因此将式(2)中的结构质量和式(3)中的不等式约束条件都采用惩罚函数法, 转化为如下函数:

μ(m(x1,x2))=max{m(x1,x2)-m0, 0}

φ(σ(x1,x2))=max{σ(x1,x2)-σ0, 0}

ψ(x1,x2)=max{(x1+x2)-3, 0}

δ(x1)=max{x1-3, 0}

θ(x1)=max{x1-3, 0}

当以上函数均满足约束条件时, 其值为0; 反之其值为正。 因此, 本文目标优化函数转化为

F(x1,x2)=min{y1}+PF(μ(m(x1,x2)+

φ(σ(x1,x2))+ψ(x1,x2)+δ(x1)+

θ(x2))

(4)

式中:PF为惩罚因子。

根据文献[7, 13]中热-结构耦合模型有限元分析得到结构应力函数为

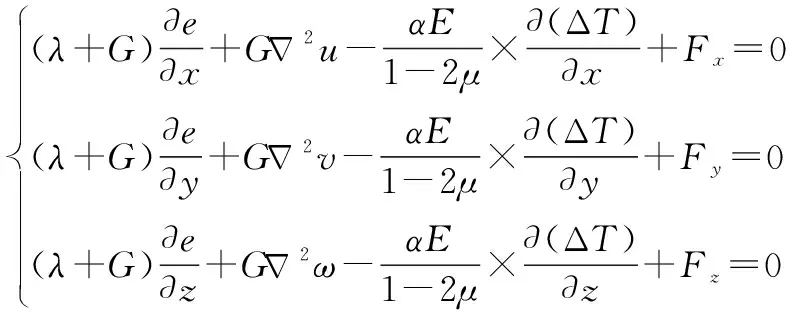
(5)

参照文献[13], 对于结构应力von Mises仿真计算方法为: 先对结构进行瞬态温度历程计算, 再选取某时刻的温度值作为载荷, 然后利用式(5)求解。 本文同样采用文献[7]中的热防护效率仿真公式:

η=100×(tout-tin)/tout

(6)

式中:tout为测点外壁温度;tin为测点内壁温度。

本文数学建模采用边界元法, 其中用到有限元分析软件中的应力单元和温度单元, 模型准确的边界条件为: 保证导弹壁宽为3 mm, 距离舱体端部16 mm; 距离舱体端部16 mm处的温度载荷最大不超过300 ℃, 导弹结构在这种温度下的最大von-Mises应力不超过396 MPa。

2 基本樽海鞘算法

设M×K维为种群觅食空间,M为觅食点数,K为种群数量。 觅食范围内食物为A={A1,A2, …,AK}T, 其相应位置为xn={xn1,xn2, …,xnk}T,n=1, 2, …,M, 其解上限为bh, 下限为bl,xM×K=rand(M,K))(bh-bl)+bl, 种群领导者位置更新为

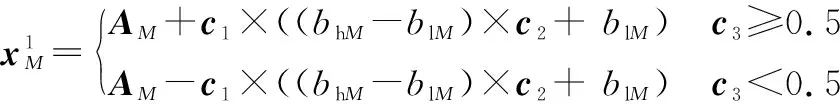
(7)

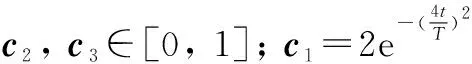
(8)

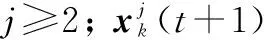
3 个体扰动多策略樽海鞘算法

针对樽海鞘算法在优化方面的不足, 提出了个体扰动多策略樽海鞘算法(Individual Disturbance Multi-Strate-gy Salp Swarm Algorithm, IDMSSA)。 新算法包括Sobol 序列, 动态权重调节机制, 早熟收敛判断机制、 变异因子和反向解策略, 以及针对本文多目标优化问题所用到的Pareto最佳解储备库, 其核心思想是提高算法性能。

3.1 初始种群均匀化处理

在算法进化过程中, 群体智能算法优化性能与初始种群分布有关, 初始种群均匀分布能够保证算法多样性, 增强算法的全局搜索能力, 提高算法效率[14]。 受文献[15]的启发, 结合初始种群分布均匀化的思想, 考虑到樽海鞘算法初始化是采取随机序列, 例如在[0, 1]之间生成维度为9、 种群数为200的随机序列初始化(如图6(a)所示), 其个体均匀分布比较差。 为加强算法全局勘探能力, 提高算法的多样性, 充分发挥初始解的作用, 引进Sobol 序列来初始化种群。 该序列在求解区间呈均匀化分布, 周期小, 采样快, 在处理高维复杂性非线性函数效率更高[16], 其在同样范围内种群分布如图6(b)所示。 对比可知, Sobol序列明显优于随机序列, 其种群分布更均匀。

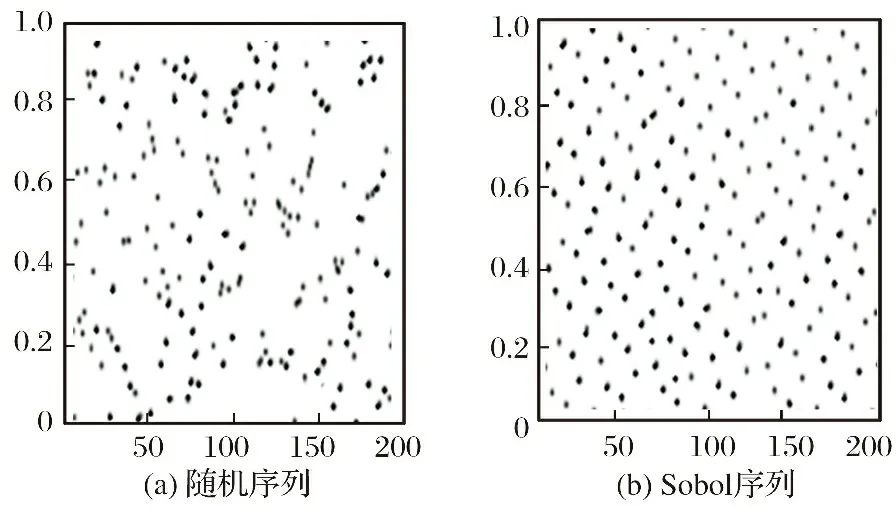
图6 种群初始化Fig.6 Population initialization

Sobol 序列公式如下:

yn=ymin+εn·(ymax-ymin)

(9)

式中:εn∈rand(0, 1);ymin,ymax为当前代个体适应值的最小值和最大值。

3.2 动态权重调节机制

通过研究基本樽海鞘算法机理及位置更新式(8)可知, 追随者只受前一个樽海鞘个体的影响, 新一代个体位置更新是由前一代相邻个体位置所决定, 相邻不同优劣个体所起作用相同, 种群没有把优势个体的优势展现出来, 优势个体对整个种群中其他个体的影响逐代下减, 使得种群群体协作能力发挥效用不佳, 降低算法的收敛速度。 受文献[17]的启发, 结合动态权重能够引领整个群体朝优化方向进化的思想, 本文引入动态权重, 充分发挥其在进化过程中优势个体的引导作用, 减少劣势个体带来的不良影响, 摆脱追随者对前一个樽海鞘位置的完全依赖。 因此, 种群中樽海鞘个体能够根据优势权值动态变化, 不仅有利于提高搜索的灵活性, 还能增强整个算法勘探和开发能力, 从而进一步提升算法速度。 假设种群规模有N个个体, 其适应度分别为f1,f2, …,fN, 相对应的权重为w1,w2, …,wN, 则新一代位置更新按照式(10)进行:

(10)

动态权重wi为

(11)

3.3 早熟收敛判断机制、 变异因子和反向解策略

由式(10)可知, 动态权重调节机制确实能够使算法朝着最优解的方向搜索, 其变化能强化进化过程中优势个体的影响, 同时也弱化了优势个体进入早熟时, 算法难以跳出局部最优的能力, 从而降低算法收敛速度。 为此, 引入早熟收敛判断及早熟处理机制。 该机制能够有效地根据所处状态实时脱离局部最优, 提高算法效率。 局部最优早熟判断与处理如图7所示。

图7 早熟判断预处理机制Fig.7 Preprocessing mechanism of precocious judgment

早熟收敛判断是“早熟处理”的前提[18]。 研究发现, 樽海鞘算法无论是“局部收敛”还是“全局收敛”, 樽海鞘种群个体都会出现“聚堆”现象。 本文将樽海鞘个体最佳适应值的变化状态作为“早熟收敛”判断的条件, 设xavg为樽海鞘当代的平均位置,α2为樽海鞘群体位置方差[19], 定义为

(12)

式中:x为归一化因子, 主要约束α2的大小, 即

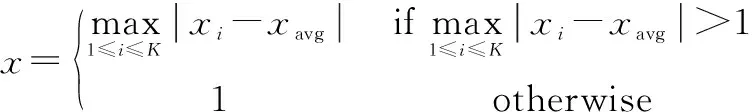
(13)

式(12)能说明当代种群个体的“堆集”程度:α越小, 说明樽海鞘种群的“堆集”程度越大。 如果算法不满足预设结束条件, 将使樽海鞘缺乏多样性而呈现“早熟收敛状态”。 当α2≤c时(c为预设常数), 则认为算法陷入“停滞”, 即算法进入早熟状态。 受文献[19]的启发, 高斯变异、 柯西变异两种函数同范围同纬度内的不同分布如图8所示, 考虑到柯西变异比高斯变异更具有优势(其分布区间较大而且紧凑), 充分利用其分布函数“横轴具有较大或较小的值, 纵轴也有一定概率得到相应的值”的思想, 即对种群个体的最优位置施加一个变异扰动, 使其发挥强大的局部调节能力, 进而帮助算法跳出局部最优, 克服早熟的不足, 提高了算法的求解精度。

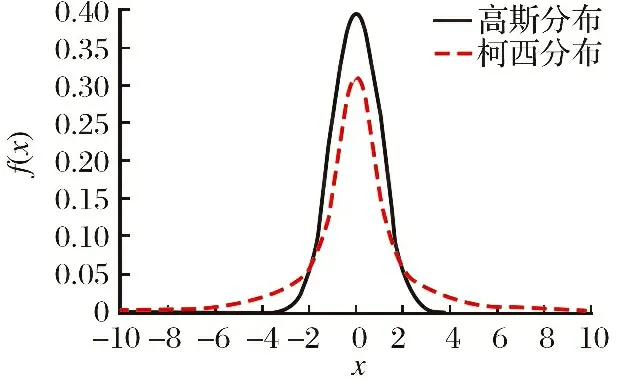
图8 高斯、 柯西变异分布Fig.8 Gaussian and Cauchy variation distribution

对局部早熟最优解进行柯西变异:

x(t+1)=Cauchy(0, 1)⊕xbest(t)+xbest(t)

(14)

式中:xbest为当代最优解; Cauchy(0, 1)为标准柯西分布。

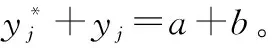
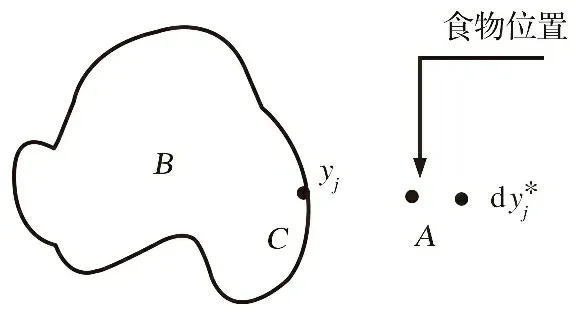
图9 C点情况图Fig.9 C point situation diagram

设Y=(y1,y2, …,yd)为d维空间的一点,yj∈[aj,bj],j∈1, 2, …,d, 则yj的反向解为

(15)

3.4 多目标Pareto最佳解替换机制

与单目标函数优化不同, 多目标函数优化的最优解不一定是满足实际需要的最佳解。 因此, 受文献[22]的启发, 结合本文多目标函数优化目标的特点, 引入两个存储种群最佳解集合: 当代种群进化集合X(t)和Pareto最优解临时储备库M, 其集合数目都为n。 二者的不同之处在于X(t)仅是理论上的最佳解, 而Pareto最优解临时储备库M不仅是理论上的最佳解还是符合实际需要的最佳解。 随代逐步进化替换, 其中Pareto最优解临时储备库M进行更换的公式[23]如下:

(16)

式中:x,y为两个不同种群个体;ε为调节Pareto最优解间隔常数。 编程实现时, 在常数基础上逐渐减小ε的大小, 直到种群数量达到规定的群体规模数, 这样得到当前种群中Pareto最优解, 即Pareto最优阵面。

3.5 算法流程图

个体扰动多策略樽海鞘算法从多方面增强樽海鞘算法的寻优性能, 其算法流程如图10所示。

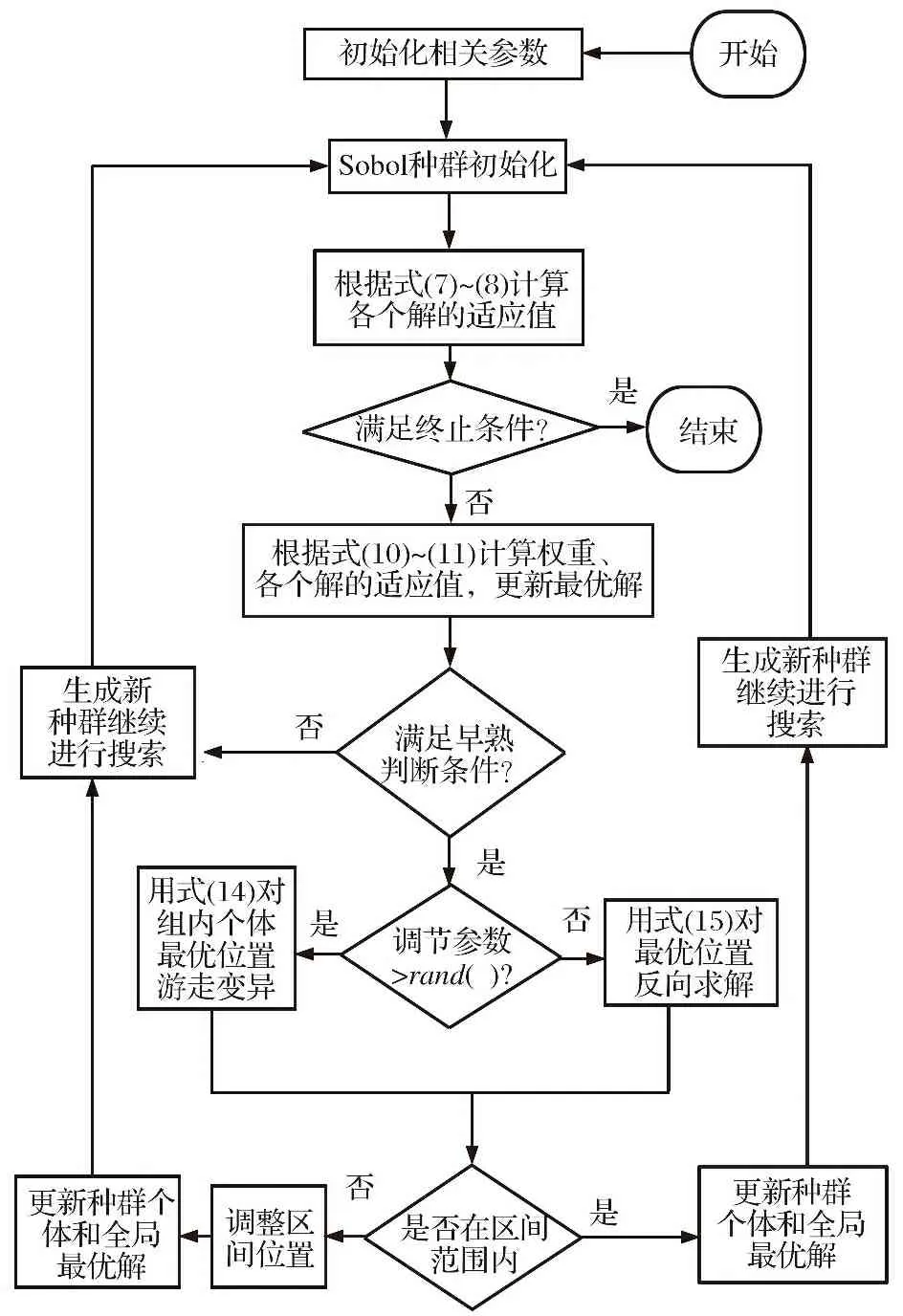
图10 算法流程图Fig.10 Algorithm flow chart

4 仿真实验及其分析

为了充分验证每个策略对算法性能的影响, 与文献[7]中的遗传算法(GA)进行仿真实验对比。 设基本樽海鞘算法为SSA, 单增Sobol 序列策略樽海鞘算法为SSA1, 单增动态权重调节机制樽海鞘算法为SSA2, 单增早熟收敛判断机制、 变异因子和反向解策略樽海鞘算法为SSA3。 所有对比算法均在相同仿真平台上进行演示, 进化种群数量均设置为30, 最大进化代数Tmax= 100,ε=0.001,c=0.01,n=10, 其他参数与文献[7]相同。 遗传算法中, 交叉因子为0.7, 变异算子为0.1。 实验仿真结果输出后, 在Pareto最优解临时储备库M中输出实际需要的最佳解, 如表2所示。

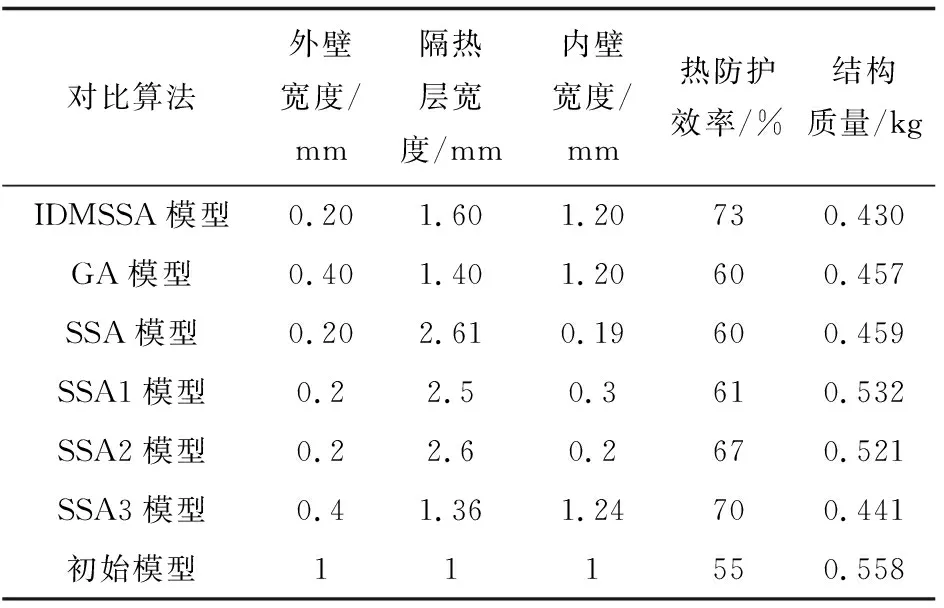
表2 不同算法最优解对比Table 2 Comparison of optimal solutions of different algorithms

由表2可知, 在热防护效率方面, SSA3>SSA2>SSA1>SSA。 这说明, 早熟收敛判断机制、 变异因子和反向解策略对算法性能作用较大, 动态权重调节机制对算法性能作用次之, Sobol 序列策略初始均匀化对算法性能的作用较小。 主要原因在于SSA3能够通过早熟判断机制进行位置变异而跳出“局部最优”, 提高了算法精度。 3种改进算法所得结果都优于基本樽海鞘算法的优化结果, 说明不同的改进算法都是有效的, 只是不同策略对改进算法性能的贡献大小不同。

整体来看, 6种不同优化算法都优于初始模型所得热防护效率和结构质量这两项指标的优化结果, IDMSSA模型最优解中热防护效率为73%, 明显优于其他对比算法, 而且其所求结构质量也是所有算法中最小的。

从导弹结构热防护的优化目标函数角度可知: (1)要满足结构热防护效率越大越好; (2)所求导弹结构质量越小越好; (3)要满足距离舱体端部16 mm处的温度不超过300 ℃, 并且导弹结构在该温度下的最大von-Mises应力越小越好, 最大不超过396 MPa(与300 ℃相对应), 其最理想的结构最大应力为392 MPa。

根据式(5)和文献[6]中热-结构耦合分析方法流程图, 可计算出本文改进算法求得的温度为294 ℃, 导弹结构最大von-Mises应力为379 MPa; SSA所得温度为297 ℃, 导弹结构最大von-Mises应力为388 MPa。 与文献[7]中的遗传算法(GA)相比(所得温度为296.2 ℃, 导弹结构最大von-Mises应力为384 MPa), 本文改进算法所得的热防护效率、 导弹结构质量、 温度及对应的最大von-Mises应力都是最优的, 均优于初始模型算法和遗传算法。

本文改进算法所得的质量、 温度、 应力水平和热防护效率上均比遗传算法、 初始模型算法具有优势。 原因在于: 在过去, 基于严格机理模型所得到的优化命题通常具有方程多、 非线性强、 变量维度高、 因数多、 影响广、 难度高和规模大等特点, 这使相关量的存储及命题的求解都相当困难, 这些问题必须由一个相当有效的优化工具来进行求解。 面对大型问题, 常规的优化方法已经无能为力, 计算速度、 收敛性、 初值敏感性等都不能满足需要。 群体智能优化算法的兴起, 丰富了现在优化技术的内涵, 促进优化技术的快速发展, 成为求解现代优化问题最优值的有力工具, 为解决具有非线性、 多极值等以前难以处理的传统高维复杂优化函数提供了新的思路。 而与遗传算法相比, IDMSSA虽然也属于群体智能优化算法, 但其具有的最大优点是: 该算法引入Sobol序列策略对初始种群均匀化处理, 提高解的质量, 保持种群多样性; 使用动态权重调节机制, 更好地发挥优势个体的引导作用, 提高算法速度; 利用早熟收敛判断机制、 变异因子和反向解策略, 增强种群探索效率, 有利于算法跳出局部最优, 提高求解精度; 而遗传算法具有所求精度不高, 易陷入“局部最优”的缺点。 因此, 本文算法能够克服其不足而同时实现其质量、 温度、 应力水平和热防护效率的优势。

5 结 束 语

针对樽海鞘算法在解决高维复杂多目标函数优化方面存在多样性差、 早熟收敛及无法求得精确解等缺点, 引入Sobol序列, 动态权重调节机制, 早熟收敛判断机制、 变异因子和反向解策略来提高算法性能, 并对导弹基于波纹夹芯结构热防护一体化热防护效率、 结构质量进行仿真实验。 通过对比3种算法的优化结果, 验证了改进算法求得热防护效率、 结构质量两种参数的精度高于其他算法, 验证了改进算法的有效性和优越性。