基于优化随机森林的对地攻击无人机自主作战效能评估

邵明军, 刘树光, 李姗姗

(空军工程大学 装备管理与无人机工程学院, 西安 710051)

0 引 言

随着信息技术、 智能技术、 无人技术的迅速发展与大量应用, 无人机作为集成多种先进技术于一体的空中作战平台得到了飞跃式发展, 并在世界各国军事领域得到广泛应用。 同时, 依托各类先进技术催生出无人机新的作战形态, 也在各种作战、 演训任务中发挥着至关重要的作用。 当前, 如何衡量无人机装备对作战态势的影响程度以及把握无人机自主作战性能强弱, 是研究无人机技术发展与实际作战运用相结合的迫切需要。 建立科学合理的无人机自主效能试验评估方法是全面清晰了解无人机装备性能、 优化调整参数以提高作战能力的有效途径, 也是综合评估无人机技术和自主作战能力的关键措施。

近年来, 不少学者基于机器学习算法对无人机自主作战效能进行评估研究, 并取得丰硕成果。 文献[1]基于自适应粒子群算法优化反向传播神经网络, 建立了无人机空地作战效能评估模型, 有效避免了无人机作战效能评估的主观性和系统的不确定性, 实现了无人机作战效能的快速、 高精度评估。 文献[2]结合无人机作战使用过程, 提出了基于动态贝叶斯网络方法的无人机作战效能评估模型, 并利用Netica工具对无人机作战效能进行动态评估仿真, 验证了模型的可行性。 文献[3]为获得精确的无人机作战效能评估结果, 利用混沌粒子群算法对支持向量机超参数进行优选处理, 构建了混沌粒子群-支持向量机的作战效能评估模型, 其评估结果表明模型具有较好的计算精度和较高的评估效率。 然而, 在实际应用过程中, 以上模型也存在较多不足, 如神经网络模型训练所需时间较长存在多个极值点、 容易陷入局部极小值等问题, 贝叶斯网络模型处理高维数据、 非线性问题较为困难且计算复杂度较高, 支持向量机模型也存在超参数选取、 调节较为困难等问题。

随机森林算法作为一种机器学习算法, 目前已有较多的研究表明, 其具有训练速度快、 预测精度高、 泛化能力强、 不易过/欠拟合等优点, 能够很好处理多参数之间的非线性映射问题, 并在医学、 材料学、 地质学等[4-6]众多领域得到了广泛应用。 近年来也逐渐应用到装备效能评估方面, 文献[7]基于随机森林算法构建了作战效能评估模型, 实现了真实作战条件下运用机器学习方法对反舰导弹武器系统作战效能进行评估的目的。 文献[8]面向系统指标体系与评估结果值构建随机森林模型, 设计系统效能指标贡献率评估方法, 实现了评价指标的重要度排序。 然而, 以上基于随机森林算法构建评估模型时, 没有充分考虑模型本身对性能参数的要求, 仅依靠系统自身随机或者主观设置参数, 势必会引起模型效率低下无法发挥出最佳性能, 进而影响效能评估结果。 因此, 为解决随机森林超参数选择主观性强、 泛化能力差、 评估效率低下等问题, 本文引入了向量加权平均算法对随机森林模型参数进行寻优, 通过向量的不同加权平均规则, 来达到快速寻优目的, 最终建立基于向量加权平均算法优化随机森林的无人机自主作战效能评估模型, 通过实际算例, 与其他机器学习方法对比, 验证了该模型的有效性和实用性。

1 基于随机森林算法的理论基础

1.1 随机森林(RF)算法原理

随机森林算法是2001年由Leo Breiman提出的一种基于决策树算法和Bagging算法结合而形成的机器学习算法[9], 同时也是一种现代分类和回归技术。 其核心内容为集成学习, 实质是由若干决策树组成的分类器, 通过组合多棵随机形成的决策树, 形成一个预测性能更加稳定的强分类器, 最终由所有决策树的预测结果决定模型的输出值[10]。

1.1.1 决策树算法

决策树是一类常见的机器学习算法, 是基于树的结构来进行决策的一种算法, 可以用于解决分类或回归问题。 典型的决策树是由根节点、 中间节点和叶子节点构建而成, 根节点是所有样本数据的集合, 以此为起点自顶向下递归构建, 并按照一定规则对样本特征提取、 分类划分形成中间节点, 继续递归构建, 最终形成具有相似特征的数据子集, 称为叶子节点。

在决策树的构建过程中, 如何确定节点的最优分裂准则, 是构建随机森林模型是否可靠的关键, 当前关于节点分裂法则在分类问题中主要使用信息增益、 信息熵、 Gini系数; 在回归问题中主要使用均方误差、 平均绝对误差准则等[8]。 由于对作战效能的评估结果需要所有决策树共同决定, 本质上为回归预测问题, 因此, 根据最小均方误差准则, 可以实现决策树节点的分裂, 即在分裂样本的对应节点处按照最小均方差准则, 采用二元递归分裂方法将样本划分为2个样本集, 求出同时满足2个样本集均方误差最小以及均方误差之和最小条件下的特征及特征值划分点。 损失函数为

(1)

式中:A为随机抽样样本;s为对应的划分节点;xi为对应样本集中的特征值;yi为对应样本集中的目标值;c1和c2分别为2个样本集D1和D2的输出均值。

依据式(1), 继续对已划分的每个样本集再次进行划分, 重复操作直到满足停止条件为止, 最后将样本空间划分为D1,D2, …,Dm。 则生成的决策树数学表达式为

(2)

式中:I(x∈Di)为示性函数(当x∈Di时取1, 反之取0)。

1.1.2 Bagging算法

Bagging算法是一种并行结构的集成学习方法, 其通过Bootstrap采样法对样本实行有放回采样, 不断地提取样本直到构建出多组不同的训练样本集合, 这些样本集合分别用来训练不同的弱分类器模型, 然后将这些弱分类器模型经过一定的结合策略形成一个强分类器模型, 这个过程中弱分类器之间是相互独立的, 方法原理如图1所示。

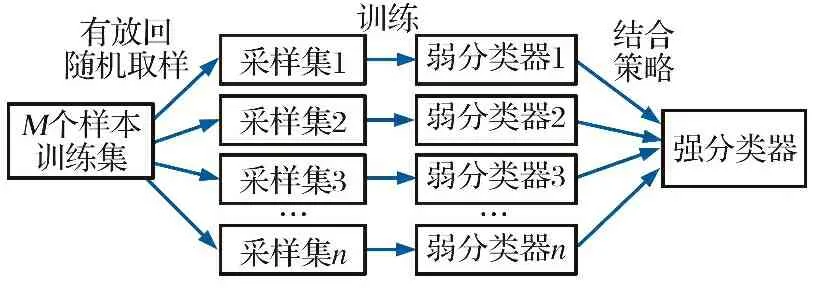
图1 Bagging算法原理图Fig.1 Schematic diagram of Bagging algorithm

1.1.3 随机森林模型

随机森林是一个由多棵决策树而形成的综合学习模型, 结合了Bagging和决策树算法, 其不仅对样本集进行随机取样, 同时对于当中的特征属性也随机选取, 从而构建出大量相互独立的决策树, 并利用每棵树对特征和样本采样的差异性, 有效降低过拟合, 提升整体泛化能力[11], 其模型表达式为

(3)

式中:N为决策树的数量;h(x,ai)为单棵决策树预测结果;fRF(x)为随机森林预测值的输出。

随机森林模型的构建主要过程为

(1) 从原始数据中采用Bootstrap抽样法随机有放回的抽取n个新的训练样本集, 并且每个样本之间相互独立, 通常每个样本集只包含原始训练集2/3的样本, 剩下1/3未被抽取的数据被称为袋外数据(Out of Bag, OOB)[12]。

(2) 对每个通过Bootstrap抽样法构建的样本集建立决策树模型, 在每个中间节点选择属性时, 从样本集的所有属性中随机抽取若干属性作为该节点的属性集, 并以最小均方误差MSE准则选取最优属性进行分裂, 直到决策树生长完全从而形成“森林”。

(3) 输入测试集样本, 每棵决策树计算生成一个预测值。 在综合所有预测值的基础上, 通过加权得出最终结果。 对于回归预测问题, 取所有决策树预测值的加权平均值作为最终预测值。

1.2 INFO优化算法

向量加权平均算法是由Ahmadianfar等于2022年提出的一种基于种群的新型智能优化算法[13], 该算法通过改进加权平均方法和更新向量来实现寻求最优解的目的, 其中更新规则、 向量组合和局部搜索是INFO算法的3个核心过程。

在INFO算法中, 通过更新规则算子可以增加最优解搜索过程中种群的多样性, 这也是区别于其他算法的本质特征, 主要由两部分组成: 一是从一组随机向量的加权均值中提取基于均值的规则并生成新的向量; 二是加入了收敛加速部分以提高全局搜索能力。 更新规则主要公式如下:

(4)

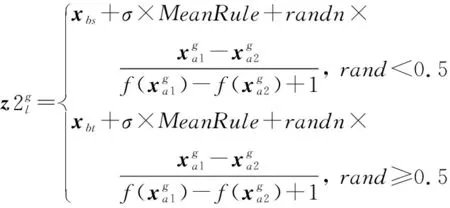
(5)

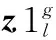
(6)

(7)

式中: Maxg为最大迭代次数;r为[0, 0.5]之间的随机数; (l=1, 2, …,Np)。

初始状态下向量加权平均函数为

(8)

(9)

种群在迭代g次后的向量加权平均函数为

(10)

(11)

式中:ε为无穷小的常数(文中ε取值为10-25);δ为加权权重因子;ω为膨胀系数;w1,w2,w3为3个权重函数;xws为第g代种群中最差的解向量。 这些解向量需要在每次迭代对种群向量进行排序后确定。

向量组合阶段, 为了增加INFO算法的种群多样性, 将前一阶段中计算得到向量与条件rand<0.5的向量相结合, 生成新的向量, 用于提高局部搜索能力:

(12)

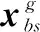
(13)

(14)

式中:φ和p为(0, 1)的随机数;xrnd为由xbt和xbs组成的新解, 这增加了算法的随机性, 以更好地在解空间搜索;v1和v2为2个随机数。

从文献[13]中可以看出, 与其他方法不同的是, INFO算法使用基于均值的更新规则来生成新的向量, 能够加快算法收敛速度。 在向量组合阶段, 将在向量更新阶段获得的2个向量组合以产生新的向量, 用于提高局部搜索能力, 这种操作在一定程度上保证了种群的多样性。 考虑到全局最优位置和基于均值的规则, 进行局部搜索, 可以有效地改善INFO算法容易陷入局部最优的问题。 因此, INFO算法可以在相对较短的时间内找到全局最优解[13], 并且具有较高的鲁棒性和适应性。

1.3 K折交叉验证

K折交叉验证是一种常用的评估模型性能的方法, 当数据集样本数较少时, 为了提高模型的泛化能力避免过拟合情况出现, 常采用K折交叉验证来检验模型性能。 其核心思想是将原始数据随机等量划分到K个子集, 其中K-1个子集用作训练模型, 剩下的1个子集用于验证模型性能。 该方法将会重复K次, 每次都会将其中1个子集用作验证集, 其余子集用作训练集, 最后将K次的验证结果取平均值作为模型的最终性能指标。 与传统重复随机抽样相比,K折交叉验证法的最大优势在于每个样本都会单独分别用于训练模型和验证模型, 从而充分利用了数据。 本文从平衡计算效率与计算精度的角度出发, 采用5折交叉验证模型。

2 无人机自主作战效能评估指标体系构建

本文以大型对地攻击无人机对敌防空区域实施侦察、 搜索、 定位目标, 并发射SDB空地导弹以及反辐射导弹摧毁、 压制敌方防空系统等任务为背景, 对对地攻击无人机自主作战效能进行研究评估。 首先, 从对地攻击无人机执行作战任务出发, 综合考虑对地攻击无人机任务过程、 影响因素, 参照效能评估指标的构建准则[14], 梳理归纳对地攻击无人机的作战效能指标, 突出作战过程中主要作战能力表现, 按照系统工程层次化结构的思路设计评估指标体系。 其次, 基于无人机作战任务, 将自主作战全过程划分为5个阶段, 并参照OODA作战环理论, 细化分解作战流程重要节点, 构建局部效能层指标; 针对作战过程中无人机所展现出的主要行为能力, 进行量化描述, 构建装备性能层指标, 对地攻击无人机自主作战效能指标体系如图2所示。

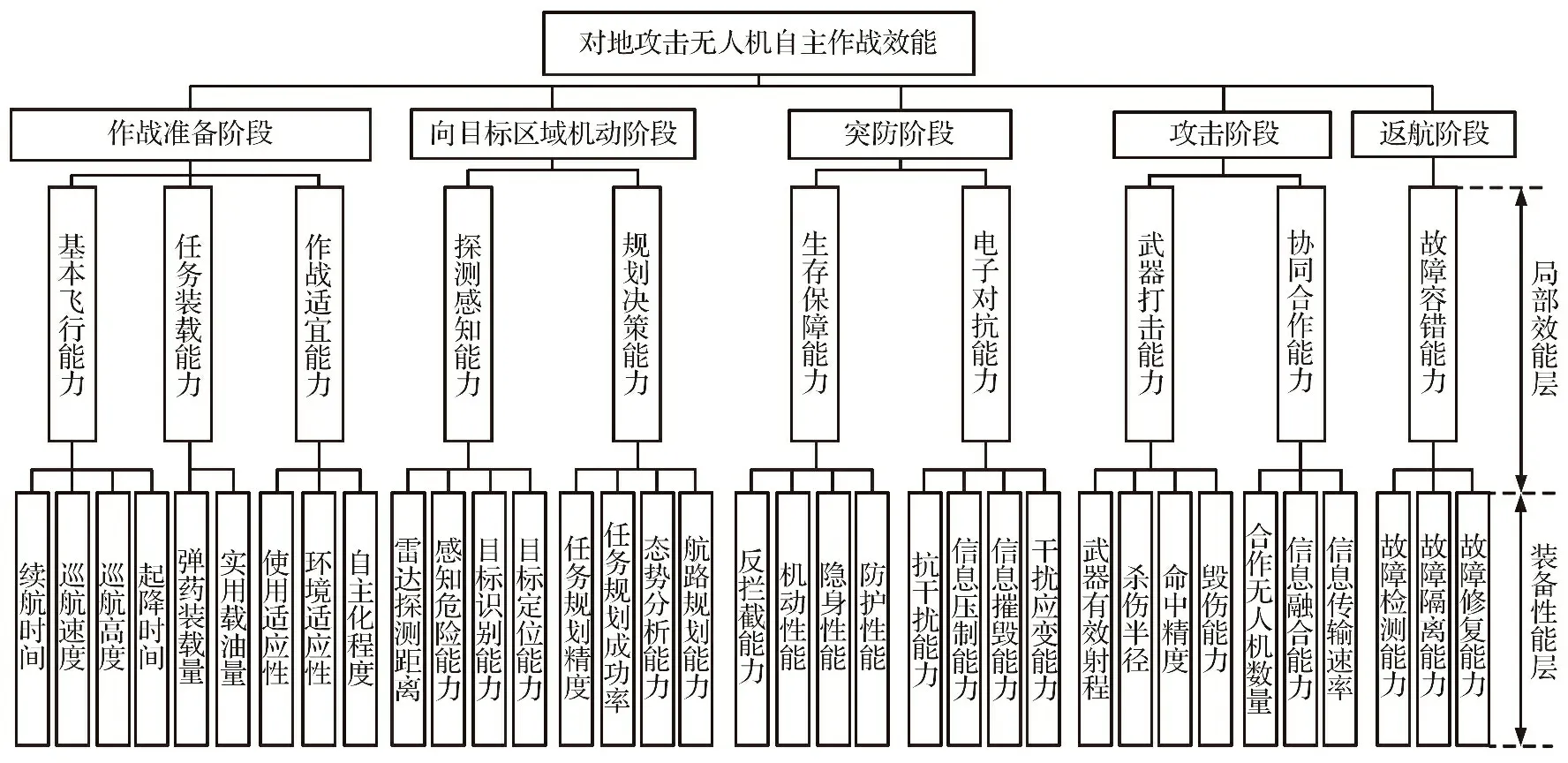
图2 对地攻击无人机自主作战效能指标体系Fig.2 Autonomous combat effectiveness index system of ground-attack UAV

3 基于INFO-RF的效能评估模型构建

3.1 超参数选取

在随机森林模型构建过程中, 由于随机森林模型中存在众多超参数, 因此在保证预测精度的同时, 选择合适的超参数对模型的构建至关重要, 本文参考文献[15]主要考虑决策树的数目与最大树深度这2个超参数对随机森林回归预测模型的影响。 在随机森林模型中, 决策树的数目越多, 模型的鲁棒性和准确率就会越好, 但是模型的训练和预测时间也会随之增加, 在数目达到一定数量后, 模型的精度反而提升不大, 并且会产生过拟合现象, 但是树的数量太小又会导致模型欠拟合, 因此决策树的数量选择对模型的影响较大; 最大树深度常用于控制模型复杂度, 深度太小可能会导致模型欠拟合, 无法捕捉数据的复杂关系, 降低了模型的准确率, 深度太大会导致过拟合, 对模型的泛化能力造成影响。 因此, 选择合适的超参数, 有效地避免过拟合的现象发生, 对模型的构建和预测结果的分析至关重要。

3.2 优化模型构建

有关RF预测模型的超参数优化问题, 大多数还是基于前向搜索方法[16]或网格搜索法[17]等寻找最优超参数, 但由于传统方法存在耗时较长, 易陷入局部最优解或因搜索步长的选择不当而错过最优值等问题, 致使RF存在较大局限性。 因此, 为了找出超参数的最佳组合, 本文引入INFO智能优化算法来对RF中决策树的数目和决策树的最大深度进行优化, 优化过程如图3所示。

图3 INFO优化RF模型流程图Fig.3 Flow chart of the INFO optimized RF model

3.3 模型性能评价指标

本文选用3种常见的统计学指标用于分析预测模型性能, 分别是平均绝对误差MAE、 均方根误差RMSE以及决定系数R2。 数学表达式分别为

(15)

(16)

(17)

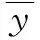
平均绝对误差MAE是用于衡量预测值与实际值之间差异的度量指标, 其表示预测值与实际值之差的绝对值的平均值。MAE越小, 说明预测值与实际值之间的差异越小, 模型的预测能力越好。 与MAE类似, 均方根误差RMSE也是用于衡量预测值与实际值差异的常用指标,RMSE越小, 表示预测结果越接近真实值, 预测结果越好。 决定系数R2是一个用于评估回归模型拟合度的统计量, 其取值范围为0到1。R2值越接近1, 表示模型对数据的拟合效果越好; 反之越接近0, 则说明模型对数据的拟合效果越差。

3.4 评估模型的实现过程

本文建立对地攻击无人机自主作战效能评估模型, 具体实施步骤如下:

(1) 读取样本数据, 并对样本数据进行归一化处理。

(2) 将处理后的数据随机分成两部分, 80%为训练数据集, 20%为测试数据集。

(3) 将训练集数据输入INFO-RF算法中, 通过向量加权平均算法进行超参数寻优, 在训练过程中, 将训练数据随机抽取划分, 并采用5折交叉验证方法, 以均方根误差RMSE作为优化目标函数, 得出随机森林模型的最优参数组合。

(4) 将测试集数据输入参数优化后的随机森林评估预测模型中, 得到预测结果。

(5) 通过对模型预测输出值和实际效能值进行比较, 并计算平均绝对误差MAE、 均方根误差RMSE和决定系数R2, 分析模型评估预测效果。

综上, 基于INFO-RF算法的无人机自主作战效能评估模型的实现过程如图4所示。

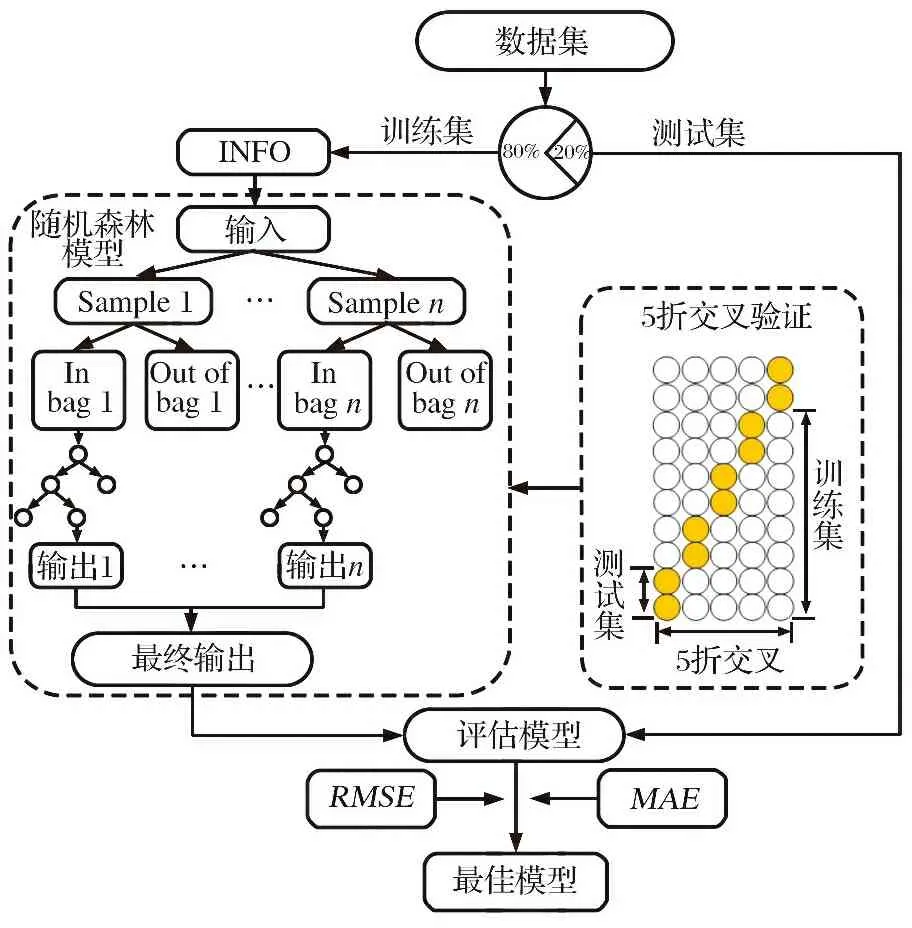
图4 评估模型的实现过程Fig.4 Implementation process of the evaluation model

4 实际算例与分析

4.1 模型参数设置

本文选取某对地攻击无人机为研究对象, 以对地攻击无人机执行压制防空作战任务为背景, 对无人机执行作战任务过程进行多次仿真实验, 并结合文献[18]中的无人机效能评估数据, 探索分析图2中各项性能指标参数情况, 将定性化指标进行量化处理, 并通过理论公式计算、 专家打分以及综合评判等方式, 得到无人机作战性能以及效能评估仿真数据, 本文选取100组数据作为评估预测模型的样本数据, 见表1。

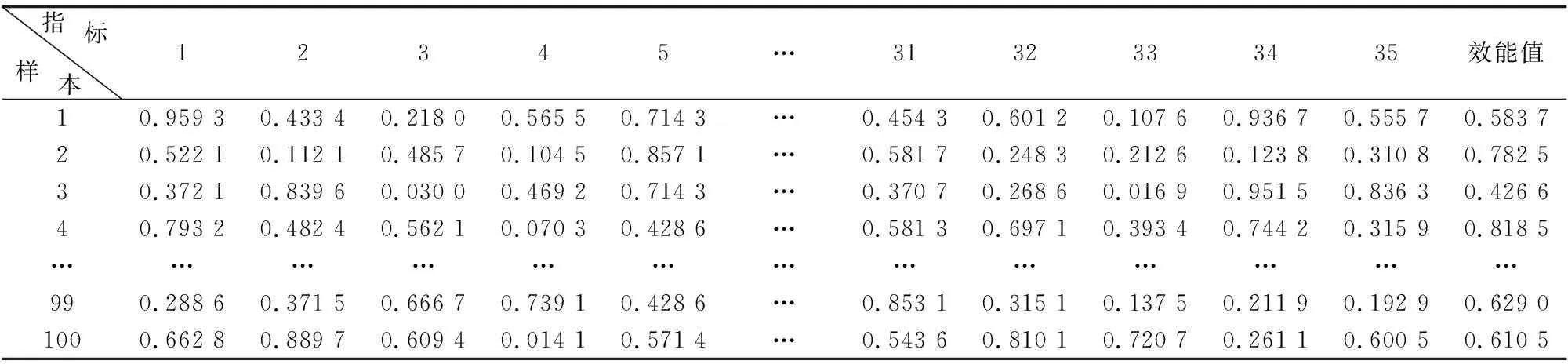
表1 归一化后的样本数据Table 1 Sample data after normalization

文中将对地攻击无人机装备性能层指标作为特征属性进行分类构建随机森林模型, 同时将随机森林中决策树的最大数量和最大深度设置为RF模型的超参数, 并利用INFO算法模型以及5折交叉验证方法对上述最佳超参数组合进行寻优。 INFO参数设置如下: 初始向量个数为5, 算法最大迭代次数为100, 在寻优过程中设置维度为2, 寻优范围分别为[50, 500]和[5, 35], 其余的超参数选取为默认值。

4.2 结果分析与评估

4.2.1 INFO-RF模型精准分析

通过图5可知, 评估预测模型在进行迭代50次左右, 适应度值达到最小且不在变化, 模型趋于稳定, 此时超参数最优组合: 最佳决策树数量为273, 最佳决策树深度为30。 图6分析可知, INFO-RF模型得出训练集预测输出值与实际效能值均方根误差RMSE为0.069 7、 平均绝对误差MAE为0.058 9, 决定系数R2为0.806 8, 均符合性能指标要求, 表明模型具有较高的拟合度和较强的可靠性, 可用于实现对目标样本的评估预测。 对比发现, 训练模型存在一定误差, 将其代入测试样本进行测试时, 由于误差传递而使部分精度降低, 故测试样本的决定系数略小于训练样本。 但总体来看, 基于优化随机森林算法的无人机自主作战效能评估模型具有一定应用性。

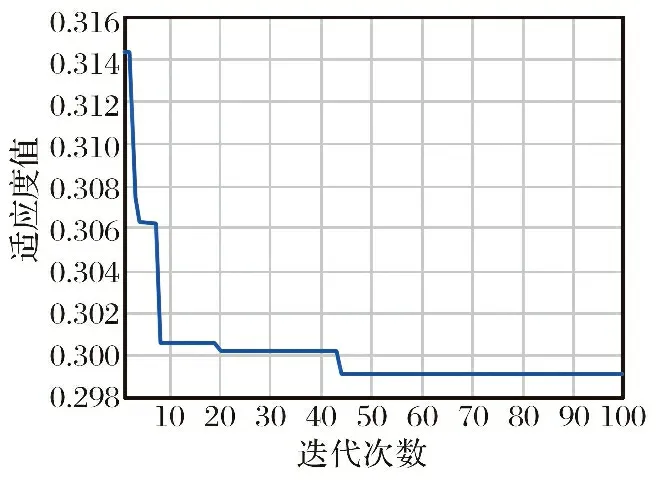
图5 INFO-RF模型迭代误差变化Fig.5 Variation of INFO-RF model iteration error

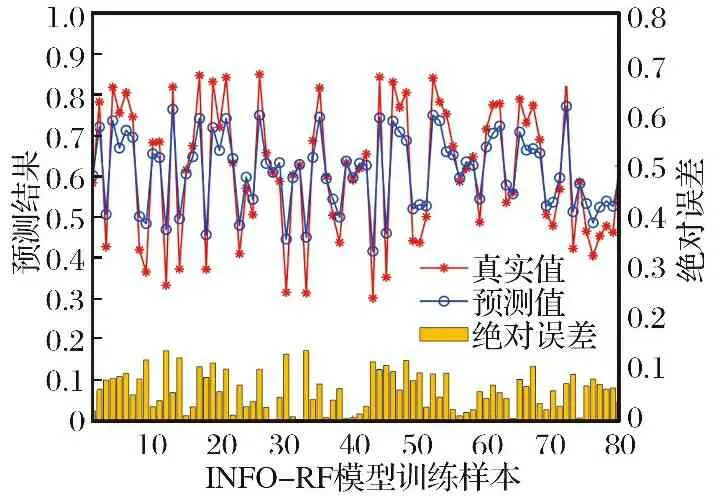
图6 INFO-RF模型训练样本预测对比Fig.6 Prediction comparison of INFO-RF model training samples

4.2.2 模型对比分析

为了验证基于向量加权平均算法优化的随机森林模型的预测性能优越性, 本文将相同样本输入INFO-RF模型、 传统的RF模型、 GA-RF模型、 SVM模型中进行比较实验, 测试样本输出结果情况如图7所示。

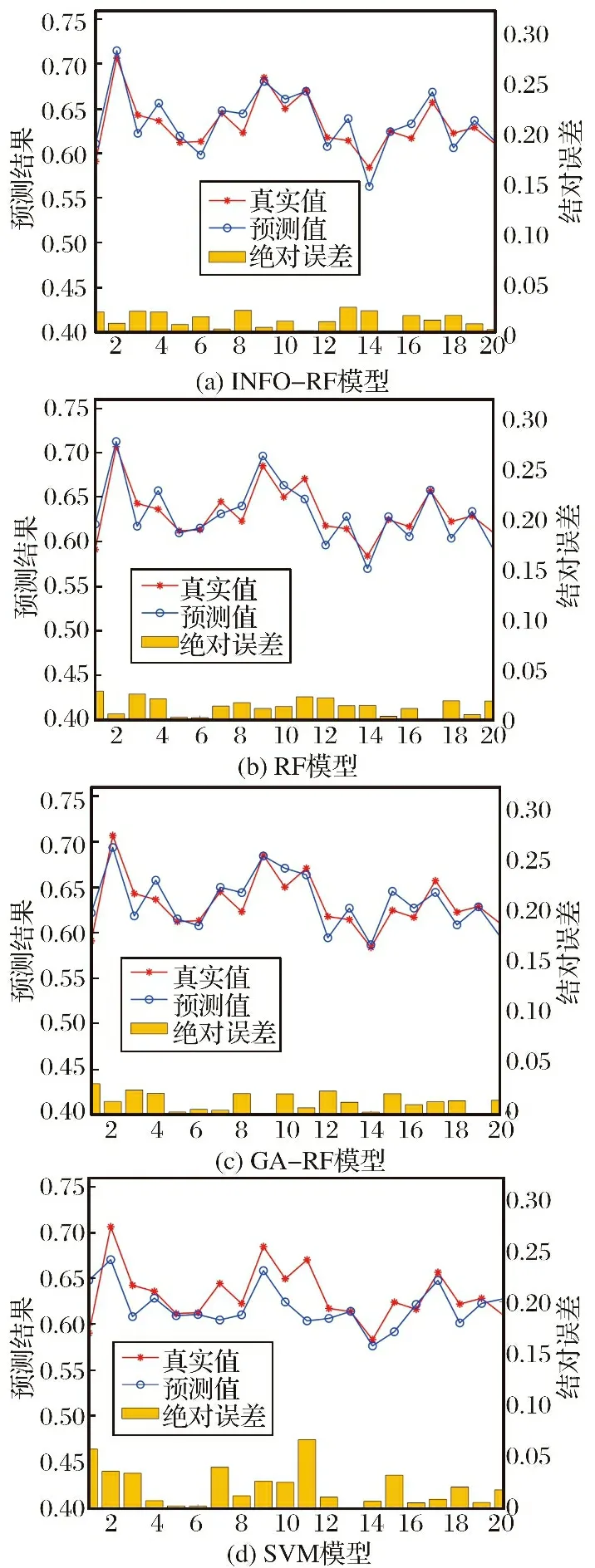
图7 多种模型测试集输出结果Fig.7 Output results of multiple model test sets

通过对比不难发现, 基于向量加权平均算法优化的随机森林模型与其他模型的表现情况基本一致, 反映出INFO-RF模型预测评估结果具有一定合理性。 从绝对误差分布情况来看, 各种模型预测输出值与实际效能值之间最大误差大致在0.05左右, 说明各模型精度较高, 能够将误差控制在较小范围, 但与其他模型相比, INFO-RF模型误差分布更小, 表现更加稳定。 通过表2及数据分析可以看出, INFO-RF模型的各项性能指标均优于其他模型, 预测输出值与实际效能值拟合程度相较其他模型较高, 更加符合实际的评估结果。 同时, INFO优化后的RF模型相较于GA-RF模型精度有所提高, 但相比传统RF模型性能提升明显, 能够展现出较强的泛化能力。

表2 多种模型预测结果对比Table 2 Comparison of prediction results of various models

4.2.3 评估指标的重要性分析

INFO-RF模型可以通过袋外数据OOB对特征变量的重要性进行分析, 在回归预测模型中通常采用均方误差MSE变化量来评判特征的重要性, 如果改变某个特征变量, 袋外数据的准确率大幅下降, 说明这个特征对于样本的预测结果有很大影响, 进而说明其重要程度比较高[19], 各项特征指标对评估结果的重要性如图8所示。

图8 特征指标的重要性Fig.8 Importance of characteristic indicators

通过分析特征的重要性可以看出, 无人机抗干扰能力、 毁伤能力、 故障检测能力在所有指标中比重较大, 对作战效能影响程度较大; 其次是续航时间、 自主化程度、 隐身性能、 信息压制能力以及故障修复能力等。 因此, 基于随机森林模型的效能评估方法不仅能够对评估结果进行预测, 还可以通过特征的重要性对无人机作战过程中各项指标影响程度进行直观描述, 这将有助于效能评估分析过程中更全面、 更精准地了解各项指标的贡献度和作用, 从而更合理的优化无人机战术运用与决策部署。

5 结 束 语

本文以无人机自主作战效能评估为研究背景, 提出基于向量加权平均算法优化随机森林为理论基础的无人机自主作战效能评估方法, 通过向量加权平均算法以及5折交叉验证方法对随机森林模型最佳参数组合进行寻优, 然后利用样本数据对INFO-RF评估模型进行训练和预测, 最后通过实例验证了相较于传统RF模型、 GA-RF模型和SVM模型, INFO-RF评估模型可以得到精度更高的预测输出值, 取得了较好的评估效果。

作为一种基于随机森林模型的预测评估方法, INFO-RF模型训练速度快, 预测精度高, 待优化超参数简单, 能够很好的处理无人机作战效能与底层指标之间的映射关系, 通过训练好的INFO-RF模型进行效能评估, 避免了指标赋权、 层次分析等方法中的主观经验问题, 解决了因数据量过大造成评估过慢等问题。