一种高精度气动光学星光偏折预测方法

刘宇鑫, 王新龙*, 丁 伟, 胡晓东

(1. 北京航空航天大学 宇航学院, 北京 100083; 2. 北京控制与电子技术研究所, 北京 100038; 3. 航空工业 西安飞行自动控制研究所, 西安 710065)

0 引 言

高超声速飞行器具有飞行速度快、 突防能力强等优点, 是当前世界各国军事博弈的重要战略武器[1-2]。 受其任务需求影响, 高超声速飞行器必须具备更强的导航自主性和可靠性[3]。 基于星光折射的新型天文导航方法有自主性强、 导航精度高的特点, 因此将天文导航技术拓展到高超声速环境中进行研究, 对高超声速飞行器实现全自主导航有重要的价值和意义。

然而, 飞行器在大气层内高速飞行时与来流发生强烈的相互作用, 会在机体周围形成激波层、 边界层、 剪切层等复杂的非均匀高速气体流场[4]。 星光穿过复杂非均匀流场时会发生气动光学效应, 导致其传播方向发生偏折, 引起星光矢量测量误差。 当飞行器以马赫数3以上的速度在临近空间飞行时, 气动光学效应会使观测到的星光矢量发生几至十几角秒的偏折[5-6], 严重影响了星敏感器的测量精度, 因此对星光偏折进行预测校正的意义重大。

目前对气动光学效应星光偏折的预测方法可分为两类: 理论模型预测法与数据拟合模型预测法。 理论模型预测法是基于空气动力学理论, 建立高超声速流场的解析模型, 进而基于折射定律建立理论模型用于预测[7-8]。 但其建模过程中仅考虑了高超声速飞行器上楔面激波所导致的光线偏折, 忽略了激波后非均匀流场对光线的偏折作用, 因此其预测精度有限。 由于星光偏折角与飞行高度、 飞行马赫数、 攻角以及视线角等因素间具有复杂的非线性映射关系[9], 数据拟合模型预测法是基于实验或计算得到的气动光学偏折数据, 利用神经网络、 支持向量机等智能优化算法[9-12]拟合得到相应的光线偏折角模型, 进而实现对偏折角的实时在线预测。 但由于偏折角与其影响因素间的映射关系复杂, 具有极强的非线性特点, 这种方法需利用光线追迹法计算大量数据进行拟合, 预测精度受训练样本的影响大。 此外高超声速流场数据的网格量大且形状不规则, 光线追迹法需耗费大量的计算资源, 制约了其应用的便捷性。

本文通过分析星光在高超声速飞行器外流场中发生偏折的机理, 综合考虑激波以及激波后流场的影响, 建立了一种精确的星光偏折角模型, 进而基于星光偏折角模型设计了一种高精度的气动光学星光偏折预测方法。

1 气动光学星光偏折角模型

1.1 星光在非均匀流场中的传播路径分析

当超声速气流流过飞行器表面时, 会形成复杂的非均匀流场结构, 根据流场中气体的流动情况, 可将流场划分为如图1所示的激波与激波后流场, 进而分别分析其对星光的偏折作用。

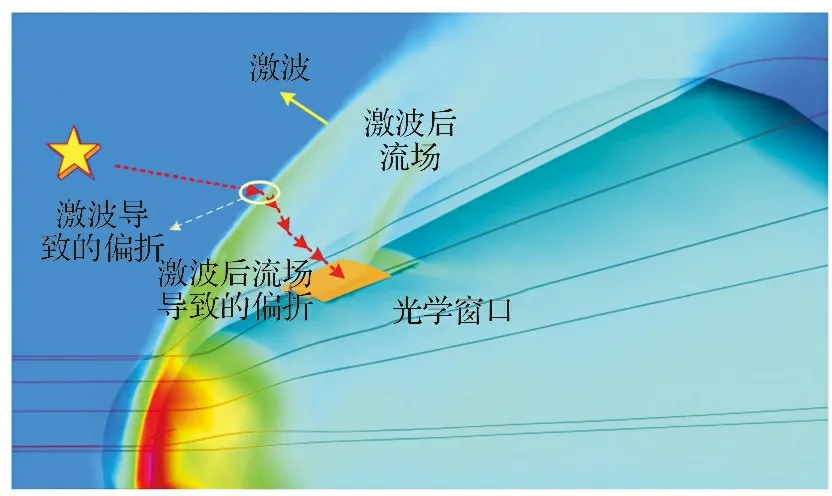
图1 星光穿过非均匀流场发生偏折Fig.1 Starlight deflects through an inhomogeneous flow field

图1中的激波是由诸多微弱压缩波堆叠在一起形成的突跃压缩波, 是高度压缩的流场形态, 会在连续介质中产生一个几乎无厚度的、 状态剧烈变化的曲面, 导致激波前后气体的密度等物理参数出现“断面”式显著变化。 超声速气流经过激波以后, 其流向折转一个较小角度, 然后气流在激波后连续地进行等熵压缩[13], 导致激波后流场气体的密度等物理参数连续变化。

由洛伦兹—洛伦茨公式可知, 气体折射率n与密度ρ间具有如下的线性关系[14]:

n=1+KGD·ρ

(1)

式中:KGD为格拉斯通-戴尔常数, 对于恒星星光所处的可见光波段, 可将其视为常值。

气体密度分布不均会导致其折射率分布不均。 星光穿过折射率分布不均的流场时会发生折射, 导致其传播方向发生偏折。 如图1所示, 星光在穿过激波面时, 由于流场气体折射率发生突变, 会发生明显的折射现象, 星光的传播方向产生较大幅度的偏折; 在穿过激波后流场时, 由于流场气体折射率连续变化, 星光会发生持续的折射, 其传播方向发生连续的偏折。 因此, 可根据星光在流场中的传播过程, 分别建立激波以及激波后流场导致的星光偏折角模型。

1.2 激波导致的星光偏折角模型

在星光传播过程中, 当其以入射角η0射入激波时, 发生偏折的示意图如图2所示。

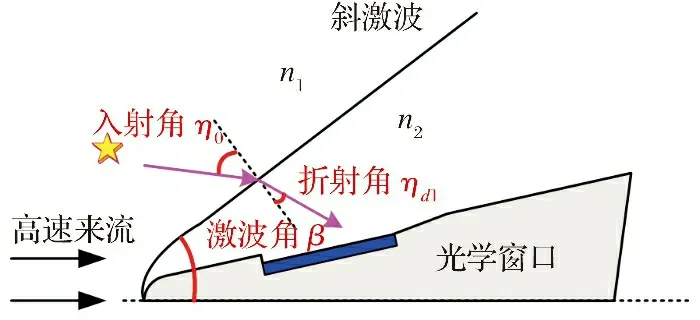
图2 星光在激波处发生偏折Fig.2 Starlight deflects at the shock wave

根据Snell定律[14]可计算得到星光在激波界面处的折射角ηd1:

(2)

式中:n1、n2分别为激波前后流场气体的折射率。

由此, 可得激波所导致的星光偏折角Δηs为

(3)

将式(1)的洛伦兹—洛伦茨公式代入式(3), 可得

(4)

由式(4)可知, 激波导致的星光偏折角受激波前后的气体密度ρ1、ρ2与星光入射角η0的影响。

激波前气体的密度ρ1为来流气体的密度, 与高度h近似成指数关系:

(5)

式中:ρ0为高度h0处的大气密度;H为密度标尺高度。

而激波后的气体密度ρ2又可根据激波关系式计算得到[13]:

(6)

式中:γ为气体的比热比, 对于空气取γ为常值1.4;M1为来流马赫数;β为激波角, 即激波与气流速度间的夹角, 对于锥形体而言, 激波角可通过求解Taylor-Maccoll方程计算得到[13], 计算所得激波角β与半锥角δ和马赫数M1的关系曲线如图3所示。

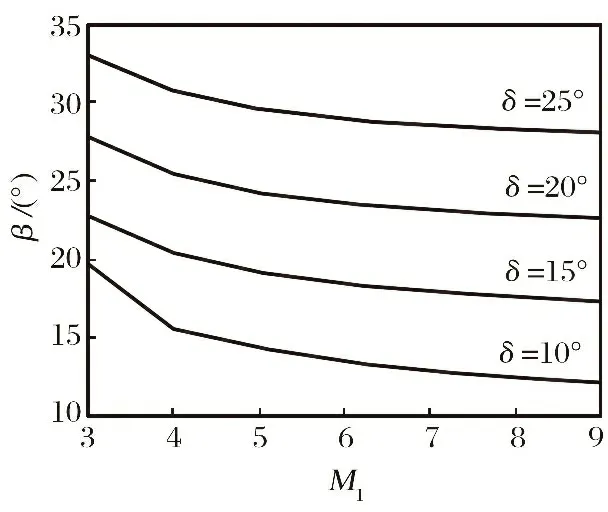
图3 锥面激波的半锥角、 激波角及马赫数关系曲线Fig.3 Relationship between half cone angle, shock angle and mach number of conical shock wave

将式(5)～(6)代入式(4)的偏折角计算公式中, 可得激波导致的星光偏折角模型为

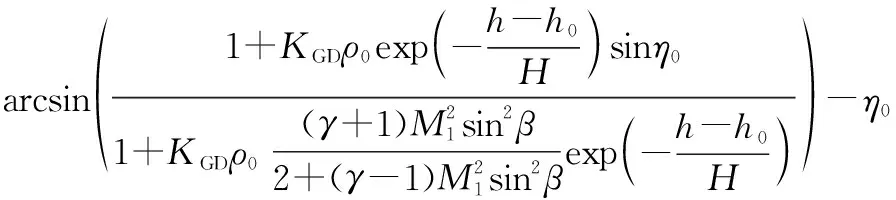
(7)

由式(7)可知, 激波导致的星光偏折角受飞行高度h, 飞行马赫数M1, 激波角β以及星光入射角η0的影响。

1.3 激波后流场导致的星光偏折角模型

超声速气流经过激波以后, 在激波后流场中连续等熵压缩[13], 使得激波后流场的折射率连续变化, 进而引起星光的连续偏折, 如图4所示。

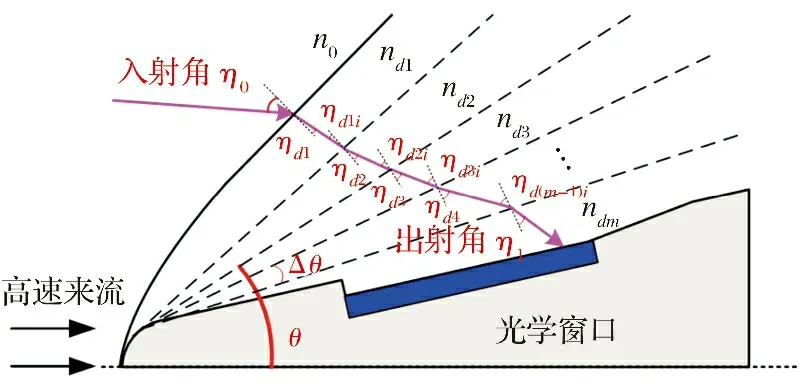
图4 星光在激波后流场发生偏折Fig.4 Starlight deflects in the flow field behind shock wave

根据锥形流理论, 绕轴线旋转而成的任意一个中间锥面上, 所有气流参数都均匀分布[13], 因此可以Δθ为角距离将激波与壁面间的流场划分为m个子层, 使得折射率在每个子层内保持恒定。

星光在激波处发生折射后以ηd1角度射出, 遇到第1个子层。 在该界面处的入射角为ηd1i, 折射角为ηd2, 在该界面应用Snell折射定律可得

(8)

由几何关系可知, 星光在第2个子层的入射角ηd2i为

(9)

在连续的中间界面处应用Snell定律, 可得星光在第m个子层发生折射后最终的出射角η1为

(10)

由此可得激波后流场所导致的偏折角Δηf为

Δηf=η1-ηd1-β=η1-ηd(m-1)i+ηd(m-1)-

ηd(m-2)i+…+ηd2-ηd1i=

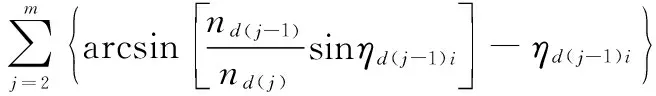
(11)

将式(1)代入式(11), 可得

(12)

由式(12)可知, 激波后流场导致的星光偏折角受各激波子层密度ρd(j)的影响。

各激波子层密度可通过对式(13)的球坐标系下的Taylor-Maccoll方程组进行数值积分, 并结合气体的等熵压缩方程计算得到[13]:

(13)

式中:vr为径向速度;vθ为轴向速度。

该方程组的求解可以使用Runge-Kutta方法, 以式(14)所示的紧靠激波后的流场速度作为初始条件进行积分求解:

(14)

式中:T1为来流气体温度;h*为滞止焓;R为理想气体常数。

各子层的气体密度受飞行高度h, 飞行马赫数M1, 激波角β以及子层位置的影响, 而激波角又可根据飞行马赫数, 飞行攻角以及半锥角计算得到, 因此可将各子层的气体密度ρd(j)表示为飞行高度h, 飞行马赫数M1, 飞行攻角α, 飞行器半锥角δ以及子层数j的函数, 即

ρd(j)=f(h,M1,α,δ,j)

(15)

将式(15)代入式(12)的偏折角计算公式, 可得激波后流场导致的星光偏折角模型为

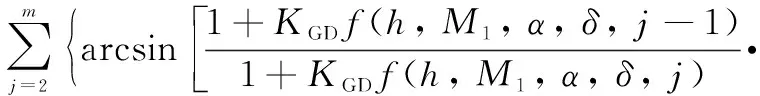
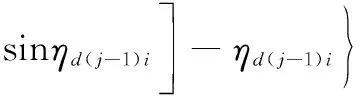
(16)

综合考虑式(7)的激波导致的星光偏折角模型及式(16)的激波后流场导致的星光偏折角模型, 可得气动光学效应所导致的星光偏折角为

Δη=Δηs+Δηf

(17)

式(17)推导的为星光矢量与折射点法线所构成平面内的偏折角, 为便于对星光偏折进行补偿, 可以星敏感器坐标系(s)为基准, 将星光偏折角分解为沿Xs和Ys方向的分量Δηx和Δηy。 定义如图5所示的星光入射角。

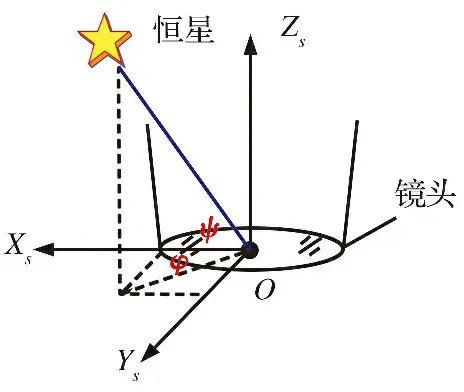
图5 星光入射角示意图Fig.5 Diagram of starlight incidence angle

图中星光矢量倾角ψ为星光矢量与XsOYs平面间的夹角, 星光矢量滚转角φ为星光矢量在XsOYs平面内的投影与Xs轴间的夹角。 根据几何关系可得星光偏折角在星敏感器坐标系下Xs和Ys方向的分量Δηx、 Δηy为

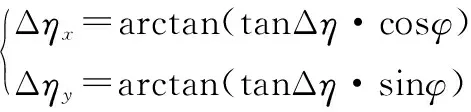
(18)

将式(17)代入式(18)后, 可得气动光学效应所导致的星光偏折角模型, 进一步可基于该模型对气动光学效应星光偏折角进行实时预测。

2 基于星光偏折角模型的偏折预测方法

通过建立的星光偏折角模型式(18)可知, 为计算星光偏折角, 需已知飞行器的半锥角δ、 飞行高度h、 飞行马赫数M1、 攻角α, 激波后流场的密度分布ρd(j)以及星光矢量入射角ψ、φ。 其中飞行器的半锥角δ在设计时已知; 飞行高度h、 飞行马赫数M1、 攻角α等飞行参数可由嵌入式大气数据传感系统(FADS)实时测量所得; 星光矢量入射角可由星敏感器测量所得, 而激波后流场的密度需通过对式(13)的Taylor-Maccoll方程组进行数值积分, 并结合气体的等熵压缩方程计算得到。 但Taylor-Maccoll方程组的形式复杂, 对其求解的计算量大, 难以用于气动光学星光偏折角的实时在线预测。 因此, 可预先离线建立如式(15)所示的流场密度代理模型, 用于星光偏折角的实时在线预测。

2.1 密度代理模型

激波后流场各点气体密度的分布规律与飞行参数相关, 因此可利用神经网络能够充分逼近任意复杂的非线性关系的特点, 基于流场计算数据对飞行参数与激波后密度的分布关系进行拟合, 建立其密度代理模型。

BP神经网络是目前应用最广泛的网络, 其模型结构简单、 运行速度快, 适合于求解内部机制复杂的问题, 适用于本文的建模环境。 BP神经网络进行训练时, 通常使用梯度下降法来最小化损失函数, 进而更新网络的阈值和权值。 但其全局搜索能力一般, 易使网络权值与阈值困于局部最优值, 进而影响预测效果。

因此, 采用全局搜索能力强, 寻优速度快的粒子群算法(PSO)对经典的BP网络进行优化, 进而利用PSO-BP网络建立密度代理模型。

2.1.1 粒子群优化算法

粒子群优化算法是一种群体智能算法, 该算法参考了鸟群觅食的自然现象, 通过模拟鸟群间的协同合作和知识共享, 利用自身的经验和同伴中最好的经验来决定下一步的运动, 使粒子群以最短的时间寻得全局最优解[15-16]。

粒子群中各粒子依据式(19)与式(20)对自身的速度和位置分别进行更新:

(19)

(20)

2.1.2 基于PSO-BP的密度代理模型

利用PSO对BP网络进行优化, 将神经网络各层的连接权值编码成粒子, 适应度值为使用该组权值时的网络输出均方误差。 利用PSO算法, 在预设的迭代次数内搜索最优的网络权值, 进而获得神经网络中的参数。

以飞行高度h、 飞行马赫数M1、 攻角α, 以及流场中各锥面与飞行器轴线间的夹角为输入变量, 以各锥面上的气体密度为输出变量, 利用PSO-BP网络建立其密度代理模型, 流程如图6所示。

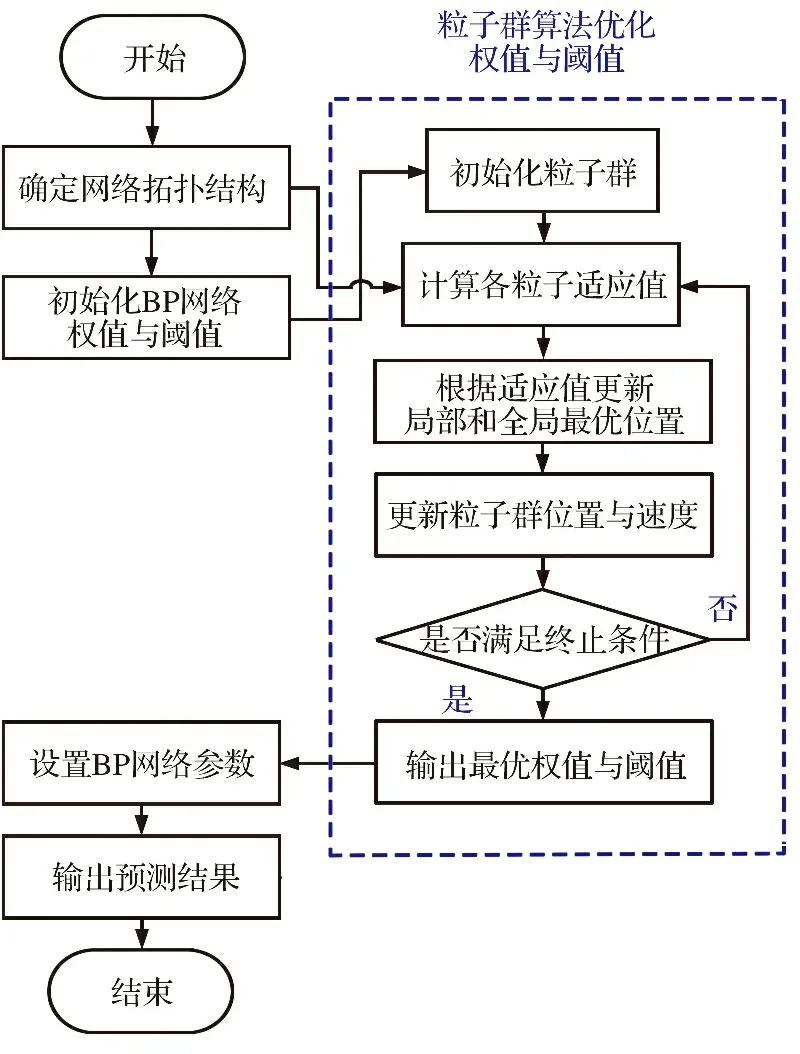
图6 PSO-BP网络算法流程图Fig.6 PSO-BP neural network algorithm flow chart

具体步骤如下:

(1) 确定BP神经网络的拓扑结构。

(2) 根据BP网络的拓扑结构, 设定种群粒子数以及粒子维数。 另设置惯性权重w、 学习因子c1和c2, 设定收敛精度和最大迭代次数, 并对每个粒子的位置和速度进行随机初始化。

(3) 将各粒子作为BP网络的参数进行训练, 将训练误差作为各粒子的适应度值, 并更新当前的局部最优解和全局最优解。

(4) 根据式(19)与式(20)对空间中的粒子的速度和位置进行不断的迭代更新。

(5) 基于迭代次数与粒子位置判断是否满足迭代终止条件。 若满足则停止迭代, 输出全局最优位置, 否则返回步骤(3), 继续迭代直至满足预设要求。

(6) 满足最大迭代次数或达到误差精度要求后终止寻优算法, 将当前的最优参数赋值给BP神经网络用于流场气体密度分布的预测。

2.2 星光偏折角预测方法

这样, 基于PSO-BP网络建立的密度代理模型并结合式(18)的星光偏折角模型, 可对星光偏折角进行实时在线预测, 该方法如图7所示。

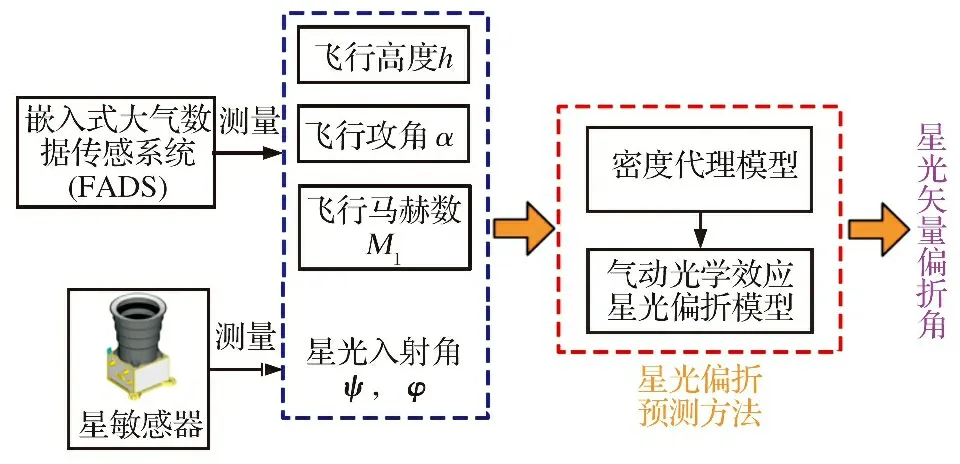
图7 星光偏折预测方法框图Fig.7 Block diagram of starlight deviation prediction method

在预测过程中, 利用FADS系统测量得到当前的飞行高度、 飞行马赫数以及攻角, 利用星敏感器测量得到星光矢量在星敏感器坐标系下的入射角。 以飞行参数作为密度代理模型的输入, 进而通过密度代理模型计算得到当前飞行状态下流场气体密度的分布, 并结合所建星光偏折角模型计算得到偏折角的预测值用于后续的校正补偿。

3 仿真验证与分析

以典型的带凹窗结构的高速飞行器为例, 对所提气动光学星光偏折预测方法的有效性进行验证。

3.1 数据集的构建

仿真中计算得到飞行速度马赫数3～9, 高度从20～50 km、 攻角从-15°～15°变化时, 不同飞行条件下的飞行器外流场。 以马赫数3、 高度20 km、 攻角0°的飞行条件为例, 其流场密度分布如图8所示。

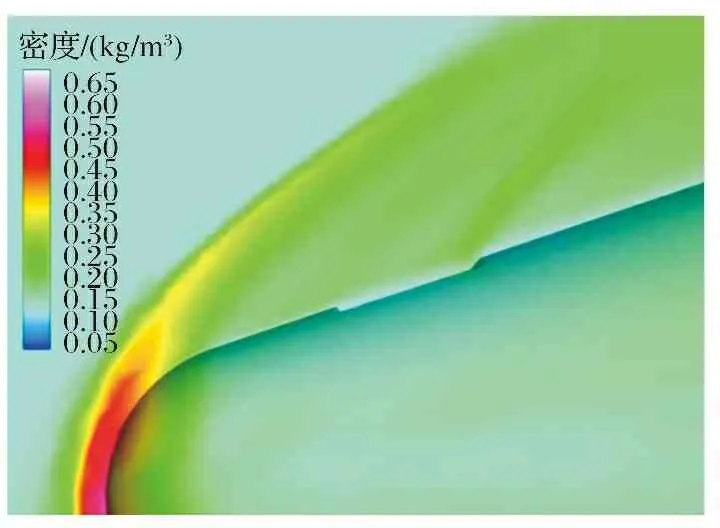
图8 流场密度分布图Fig.8 Flow field density distribution diagram

光线追迹法是通过求解光线传播方程, 从而得到光线在非均匀介质中的传输路径的一种数值计算方法。 该方法具有较高的理论精度[6], 因此仿真过程中利用四阶龙格库塔光线追迹法计算星光穿过流场后的偏折角, 并将其作为基准, 对所提星光偏折预测方法的性能进行验证与分析。

仿真中计算了星光矢量倾角以及滚转角从0°～70°变化时的星光偏折角, 部分计算结果如表1所示。

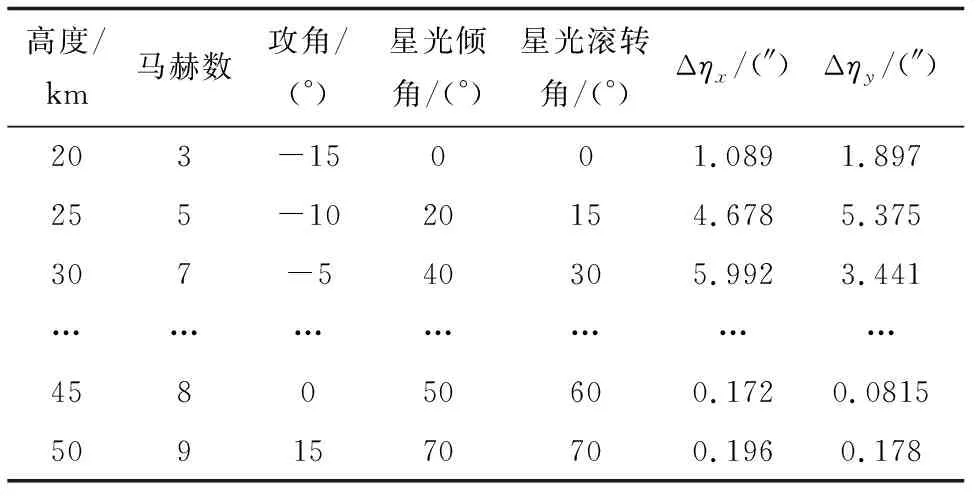
表1 星光偏折角部分计算结果Table 1 Calculation results of starlight deviationangle

由计算结果可知, 气动光学效应导致的星光偏折为几至十几角秒量级, 严重影响了星敏感器的测量精度。

3.2 密度代理模型预测结果与分析

利用计算所得的196组不同飞行条件下的流场密度分布数据, 对数据进行归一化处理后, 随机选取其中85%的数据作为模型训练样本集, 剩余数据作为模型测试样本集。

密度代理模型采用3层BP网络, 输入层节点数为4, 隐藏层节点数为7, 输出层节点数为1, 激活函数采用 sigmoid 函数, 学习速率为 0.01。 粒子群算法中的种群规模为40, 最大迭代次数为300, 学习因子c1=c2=2, 最大更新速度为5。

在利用粒子群算法寻找全局最优的权值与阈值过程中, 粒子群的适应度变化曲线如图9所示。

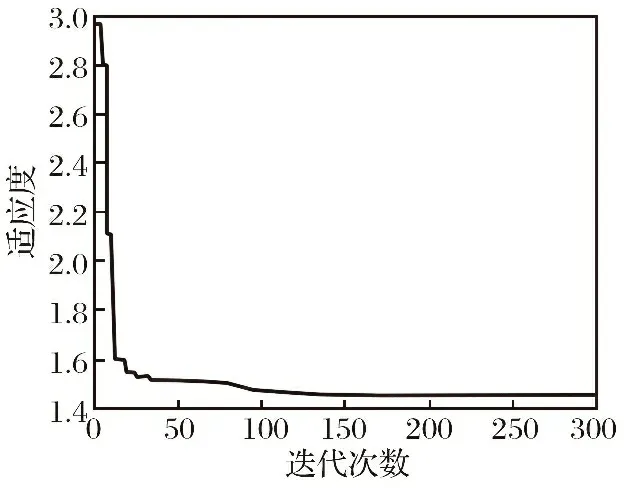
图9 粒子群算法适应度变化曲线Fig.9 Fitness curve of particle swarm optimization

由图9可知, 粒子群算法在迭代20次左右趋于平稳, 优化得到了全局最优的神经网络权值与阈值。

以马赫数5、 高度20 km, 攻角0°飞行工况为例, 由PSO-BP密度代理模型预测所得的密度分布与实际的密度分布如图10所示。 通过对比预测值与实际值可知, PSO-BP密度代理模型预测所得的密度分布规律与实际分布规律相符, 且贴合程度较高, 预测效果良好。

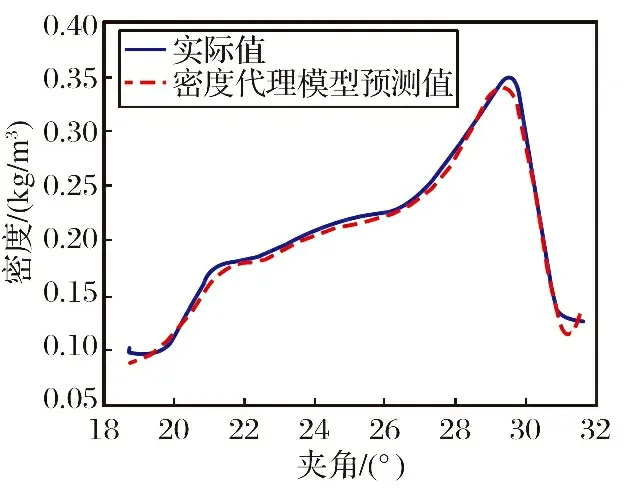
图10 PSO-BP密度代理模型预测密度分布Fig.10 Density distribution predicted by PSO-BP density surrogate model

进一步, 对PSO-BP密度代理模型在测试集上的预测精度进行统计, 得到其预测的均方根误差为0.073 9 kg/m3, 拟合优度R2为0.997 8, 能有效预测不同飞行工况下的飞行器外流场密度分布情况。

3.3 星光偏折角预测结果与分析

以四阶龙格库塔光线追迹法计算所得星光穿过流场后的偏折角为基准, 与所提方法的预测结果进行对比。 以其中100组数据为例, 预测所得的各向偏折角与偏折角的真实值如图11所示。 通过对比仿真结果可知, 所提方法的预测值与实际值保持一致, 误差相对较小。

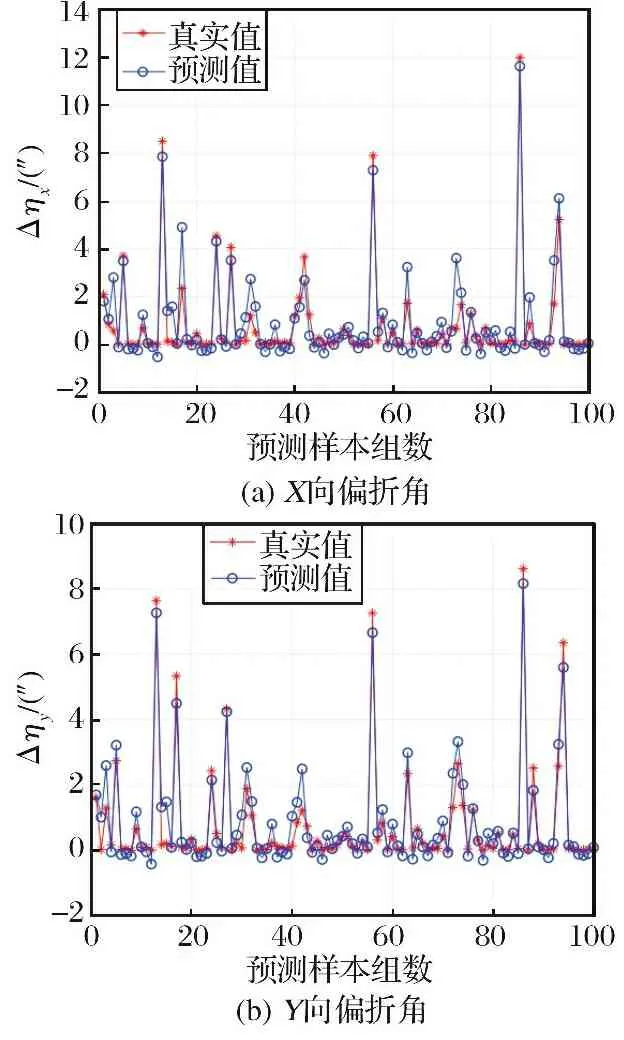
图11 星光偏折角预测结果Fig.11 Prediction results of starlight deviation angle

为进一步验证所提方法的性能, 将所提方法的预测误差与文献[9]的基于IPSO-BP网络的数据拟合模型预测法的误差进行对比, 相应的偏折角预测误差如图12所示, 其误差统计结果如表2所示。

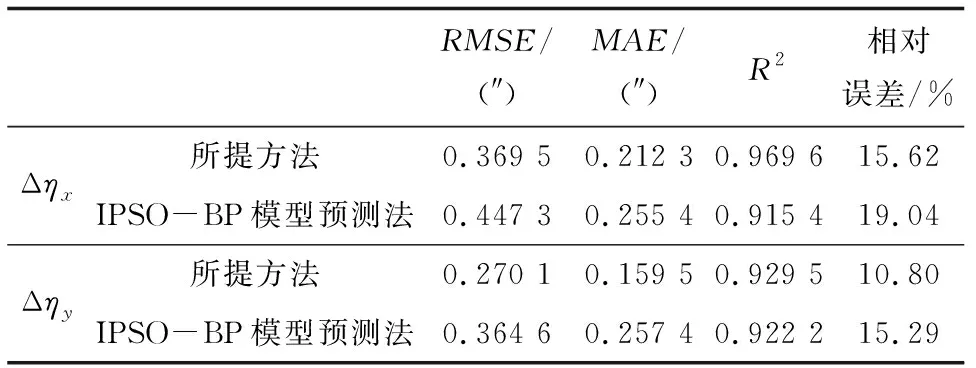
表2 星光偏折角预测精度统计结果Table 2 Statistical results of prediction accuracy

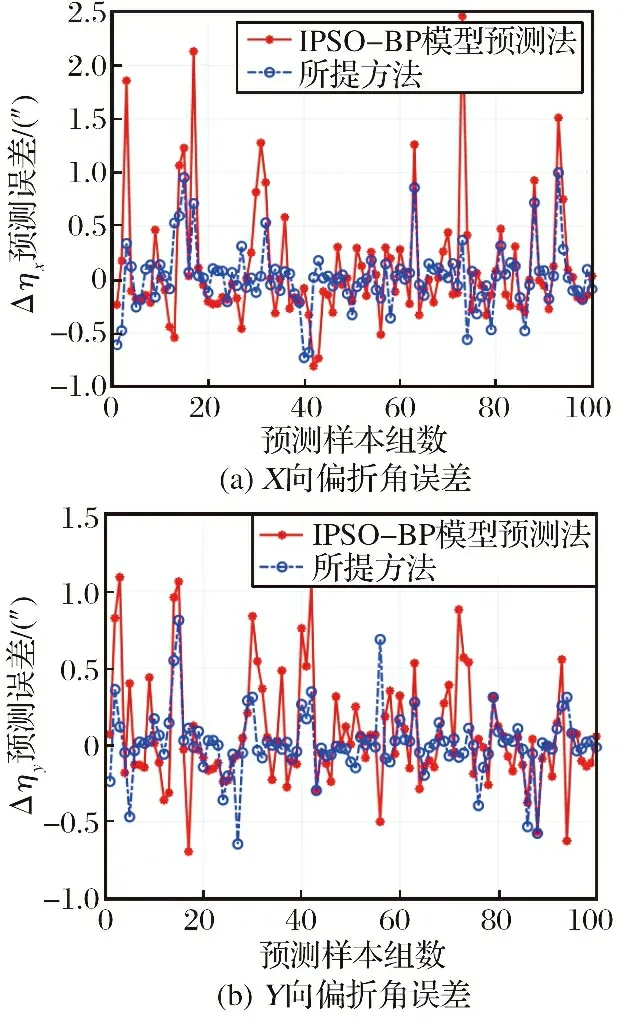
图12 星光偏折角预测误差Fig.12 Prediction error of starlight deviation angle

由表2可知, 所提方法能实现亚角秒级别的星光偏折角预测精度, 预测误差约为0.4″, 能补偿80%以上的气动光学效应所导致的星光偏折。 而虽然IPSO-BP模型预测法利用改进的PSO算法对BP网络进行优化并用于预测模型的训练, 具有更强的全局寻优和非线性拟合能力。 但受训练样本的精度以及数量限制, 其在拟合星光偏折角与攻角、 马赫数、 飞行高度、 视线倾角和视线滚转角间复杂的非线性关系时所能取得的精度有限。 所提预测方法由于综合利用了星光偏折角模型进行预测, 缓解了传统数据拟合模型预测法过分依赖训练数据的问题, 能取得较好的预测效果。 通过对比预测误差以及拟合优度可知, 所提预测方法的预测精度优于基于IPSO-BP网络的模型预测法。

此外, 基于IPSO-BP网络的模型预测法在建立预测模型时, 需利用光线追迹法计算不同入射角下的星光偏折角, 而由于高超声速飞行器流场数据的网格量大且形状分布不规则, 进行光线追迹计算需耗费大量计算资源。 与此同时, 由于星光偏折角与其影响因素间具有复杂的非线性关系, 需利用大量数据进行拟合, 在仿真中使用了2 564组数据进行训练。 而所提方法在建立星光偏折预测模型过程中, 利用所建立的偏折角解析模型替代了利用光线追迹法的数值计算过程, 仅需基于流场数据建立密度代理模型, 能大幅简化数据集的构建工作。 另外, 由于激波后流场气体密度的变化较为规律, 在训练时仅使用了167组数据即可实现比IPSO-BP网络模型预测法更高的预测精度, 能大幅度简化建立预测模型的过程, 具有较高的适用性。

4 结 论

当星光穿过高超声速飞行器外的复杂非均匀流场时会发生气动光学效应, 导致其传播方向发生偏折, 引起星光矢量测量误差进而影响天文导航的精度。 为消除气动光学效应所导致的星光偏折对天文导航的影响, 通过分析高超声速飞行器外流场的密度分布特性以及星光在流场中的传播机理, 提出了一种基于解析模型的高精度气动光学星光偏折预测方法。 与传统方法相比, 所提方法由于综合了偏折角解析模型, 缓解了传统数据拟合模型预测法过分依赖训练数据样本的问题, 能取得更好的预测效果; 另外, 所提方法避免了利用光线追迹法计算偏折角并构建数据集的过程, 解决了传统方法构建数据集时计算量大、 步骤繁琐并且会引入额外计算误差的问题, 能大幅简化预测模型的构建过程。 仿真验证表明, 所提方法在建立预测模型时能大幅减少所需的训练样本数量, 并且具有比传统数据拟合模型法更高的预测精度, 可实现亚角秒级别的预测精度, 具有较高的适用性。

另外, 高超声速环境下, 星敏感器在观星过程中还面临着高温气体辐射对星光的遮掩问题以及大气层折射效应所导致的星光矢量测量误差, 也会影响天文导航的精度。 因此, 后续将进一步研究高温气体辐射以及大气折射对星光矢量测量精度的影响情况, 以进一步提高天文导航系统在高超声速飞行器中的应用精度。