基于孔型形状系数的双相不锈钢棒材宽展模型研究

李亮，帅美荣，田恒光，王建梅，王辉绵

基于孔型形状系数的双相不锈钢棒材宽展模型研究

李亮1，帅美荣1，田恒光1，王建梅1，王辉绵2

（1.太原科技大学 重型机械教育部工程研究中心，太原 030024；2.宝武集团山西太钢不锈钢股份有限公司，太原 030003）

针对2209双相不锈钢棒材在开坯轧制阶段宽展计算精度不高、孔型设计不合理、容易产生“折叠”“耳子”等表面缺陷的问题，建立一种基于“椭圆”孔型形状系数的宽展模型，提高产品尺寸精度。建立11道次2209双相不锈钢开坯轧制有限元模型，研究轧件温度分布及“椭圆”孔型不同形状系数对轧件宽展的影响，修正传统С.И.古布金计算模型，并与实测数据进行对比，验证修正后模型的可靠性。模拟轧制过程中，轧件温度变化趋势与实测值基本相同，11道次后温降为91.87 ℃，且在孔型突变阶段降幅较大。通过轧件每道次尺寸数据对比得出，С.И.古布金模型宽展计算偏差较大，在第8道次椭圆孔型偏差最大。不同形状系数的椭圆孔型分别模拟轧制后，发现形状系数为2时，椭圆孔型充满度为93.94%，下一道圆孔型充满度为98.92%，此时轧出的产品尺寸精度高。修正后的宽展模型与实测值进行对比，计算精度高于95%。构建的形状系数修正宽展模型提高了轧制宽展计算精度，可用于指导双相不锈钢开坯轧制孔型设计及优化。

双相不锈钢；开坯轧制；数值模拟；形状系数；宽展模型

棒材开坯轧制过程中，“箱形”孔型切槽浅，轧辊强度高，允许道次变形量大，轧制耗能少且共用性好，轧制效率高；“椭圆-圆”孔型变形均匀，可有效防止局部应力的产生，轧件质量好[1-3]。因此，“箱形”与“椭圆-圆”孔型构成混合孔型系统广泛应用于棒线材轧制生产中。然而，轧件在“椭圆-圆”孔型中发生不规则塑性变形，其宽展难以预测与控制，从而影响轧件尺寸精度和力能参数计算等[4-6]。

目前，国内外学者围绕轧制成形技术进行了大量研究和应用，关于棒材轧制宽展的研究主要集中于诸如轧制速度、压下量、轧制温度、轧辊直径及润滑条件等耦合因素，并且已经形成较为成熟的关键技术研究和市场化应用。谢红飙等[7]研究了三辊减定径机组轧制棒材的宽展模型，基于伸长率为自变量的修正系数法修正采利柯夫宽展模型，单道次宽展计算结果最大偏差为10%。常彬彬等[8]基于金属流动规律，推导并验证了圆轧件在“三角孔型”中变形及三角形轧件在“圆孔型”中变形的横断面计算方法，从而避开了孔型填充系数的选取，提高了轧件横断面和宽展的计算精度。杨毅[9]研究了马氏体不锈钢95Cr18棒材连轧过程中的宽展，着重开展了轧辊摩擦系数、轧制速度和轧制温度的耦合影响研究，修正了筱仓恒树宽展公式。董永刚等[10]引入材料影响系数，修正了经典Shinokura宽展公式，并进行了迭代优化，推导出更精确的出口轧件平均等效高度和轧辊平均工作半径，大大提高了宽展预测模型的精度。Esteban等[11]探究了轧机间张力对轧件宽展的影响，用于改善轧钢产线控制器性能。Lambiase等[12]分析了压下量、摩擦因数、轧件尺寸、轧辊直径等关键工艺参数对低碳钢棒线材宽展的影响，并拟合建立了宽展经验公式来提高产品质量。

然而，国产同类不锈钢棒材质量与国外先进水平相比还有一定差距，特别是双相不锈钢产品尺寸精度和表面缺陷比较突出，因此，需要从开坯轧制源头予以控制和调整。文中将开坯孔型系统中使用频率最高的“椭圆-圆”孔型系统作为研究对象，研究椭圆圆弧曲率，即椭圆形状系数（定义为椭圆宽高比）对轧制宽展的影响规律，以及轧件在下一道次圆孔型中的成形质量，以期获得适合于2209双相不锈钢棒材的宽展计算模型，优化开坯塑性变形协调分配，提高产品质量。

1 有限元模型构建

1.1 实验材料及设备

实验材料为2209双相不锈钢，坯料尺寸为220 mm´220 mm´1 500 mm，产品为86 mm圆棒。材料成分含量见表1。轧辊直径850 mm，孔型系统为“箱-箱-箱-箱-箱-箱-变椭-椭圆-圆-椭圆-圆”，实际生产中各道次轧制速度见表2。在Gleeble-3800热模拟实验机上对2209不锈钢试样进行高温压缩实验，实测得到其应力-应变曲线如图1所示，并构建如式（1）所示本构方程。

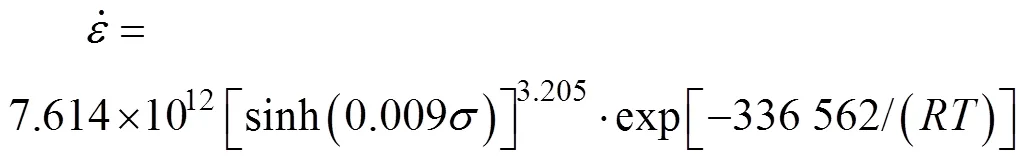
表1 2209双相不锈钢的化学成分

Tab.1 Chemical composition of 2209 duplex stainless steel wt.%

表2 11道次轧制速度

Tab.2 Rolling speed of 11 passes

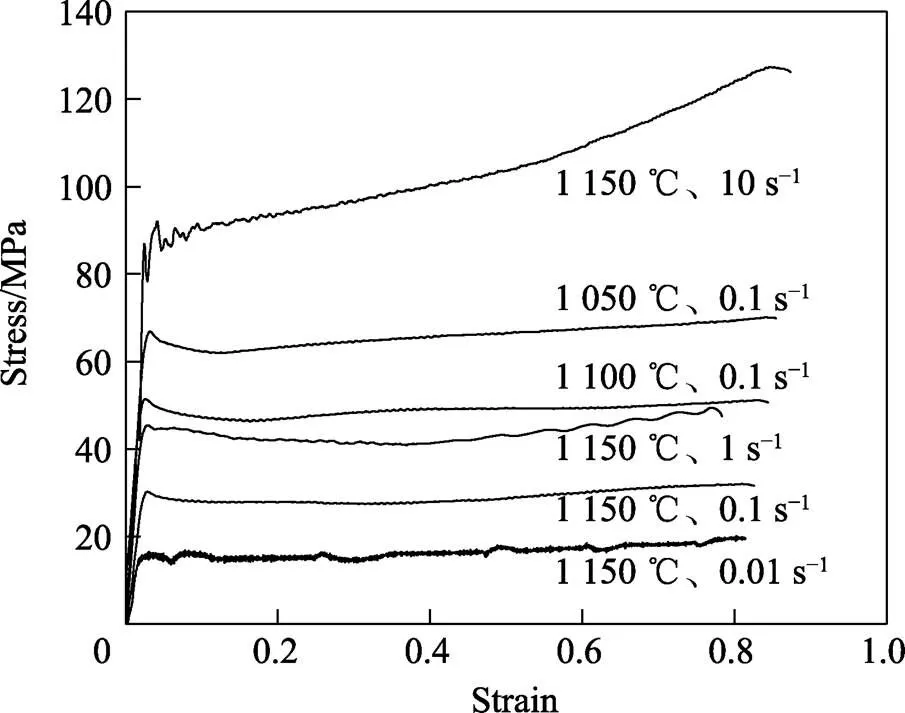
图1 2209双相不锈钢应力-应变曲线

1.2 有限元模型构建

为了建立更准确高效的有限元模型，必须了解轧制过程的基本特征，合理简化装配模型的参数、载荷和边界条件[13-18]。11道次开坯轧制模型如图2所示，假设条件如下：

1）热轧过程中，与轧件塑性变形相比，轧辊的弹性变形很小，对轧件塑性变形的影响也很小，故将轧辊定义为恒温刚性体，轧件定义为变形体。

2）轧辊与轧件材料属性为均质各向同性。

3）将开坯轧制的11道次孔型单独建模，为确保不形成连轧，孔型间距大于道次间轧件长度；且每个轧辊惯性质量均设为实际质量。

图2 有限元模型

4）轧件和轧辊均采用对称设置。

开轧温度为1 200 ℃，轧辊及环境温度为20 ℃；轧件划分网格共7 500个,类型为C3D8T，即八结点热耦合六面体单元。高温轧件与低温轧辊发生的接触定义为表面与表面接触，摩擦系数为0.35；热量交换最大为接触面热传导，接触换热系数与接触面积、界面温度、介质材料等因素有关，设为19 kW/(m2·℃)。轧件与周围空气发生自由对流，根据材料高温热导激光实验所测数据，换热系数为0.017 kW/(m2·℃)，热辐射发射率设为0.9。

2 结果与分析

2.1 各道次轧件温度分布

温度是影响轧件宽展的主要因素之一，图3为第1道次（箱形孔型）、第8道次（椭圆孔型）、第11道次（圆孔型）出口端轧件断面温度分布图。可以看出，出口断面具有相同的温度分布规律，即芯部温度基本保持不变，始终约为1 200 ℃，这是由于大棒材开坯阶段轧制速度相对较慢，应变速率小，塑性变形生热少[19]，温度基本保持不变；此外，从芯部到表面，轧件温度逐渐降低，与轧辊接触区域金属表面温度最低，其与辊缝区域的金属表面温差约47 ℃，这是轧制过程中高温轧件与低温轧辊发生热交换所致[20-21]。

11个轧制道次中，轧件温度模拟值与实测值对比如图4所示，二者变化趋势基本相同。有限元模拟结果显示，轧件温降约91.87 ℃，实测结果温降约97 ℃，二者相差5.13 ℃，偏差5.29%。周维海等[22]研究表明，氧化铁皮的存在对工件的接触传热和摩擦产生较大影响，随着氧化铁皮厚度的增大，由于其对工件的保温作用，工件温度升高。本研究中温度实测值为表面氧化铁皮的温度，因此，实测值低于轧件表面温度。此外，模拟值和实测值均显示：轧件最大温降出现在第8和第9道次，这主要是由于第8、9道次孔型形状突变，轧件与轧辊接触面大，表面接触传热程度高。这与胡韬等[23]研究的模拟结果是一致的，在孔型系统形状交变阶段，容易引起轧件温度较大幅度的下降，对于温度敏感材料的性能稳定性具有不良影响。

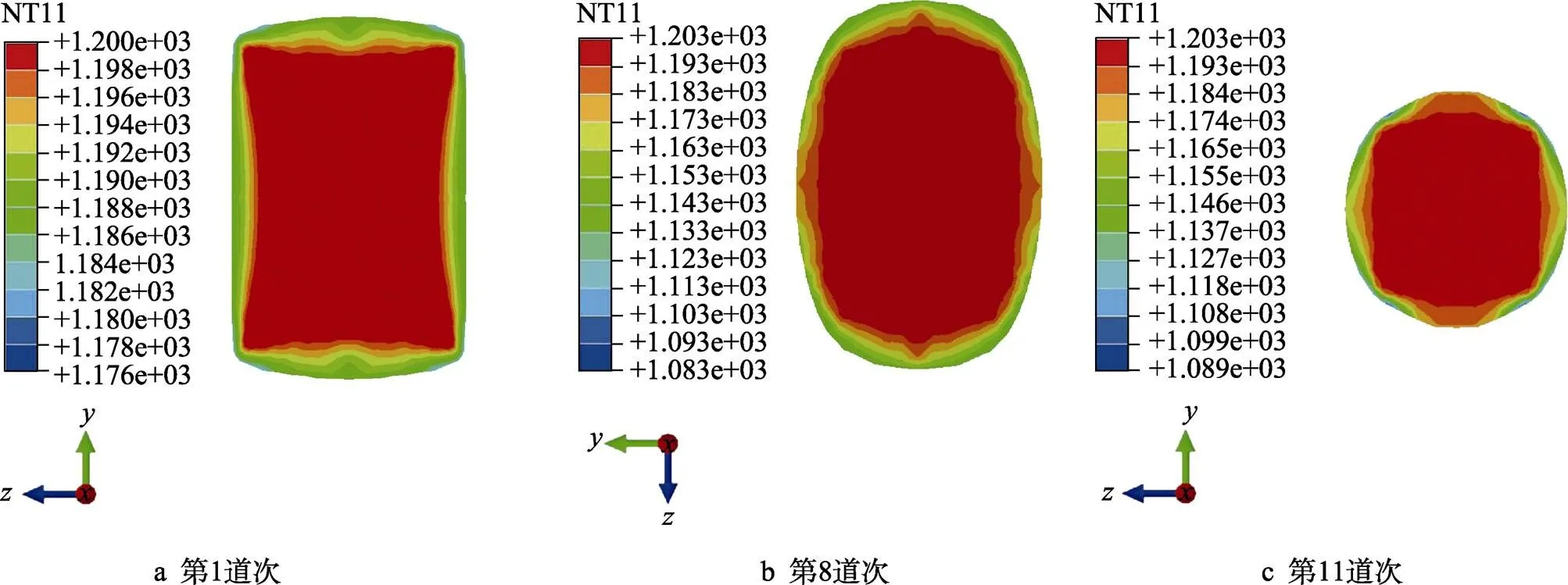
图3 轧件出口断面温度分布

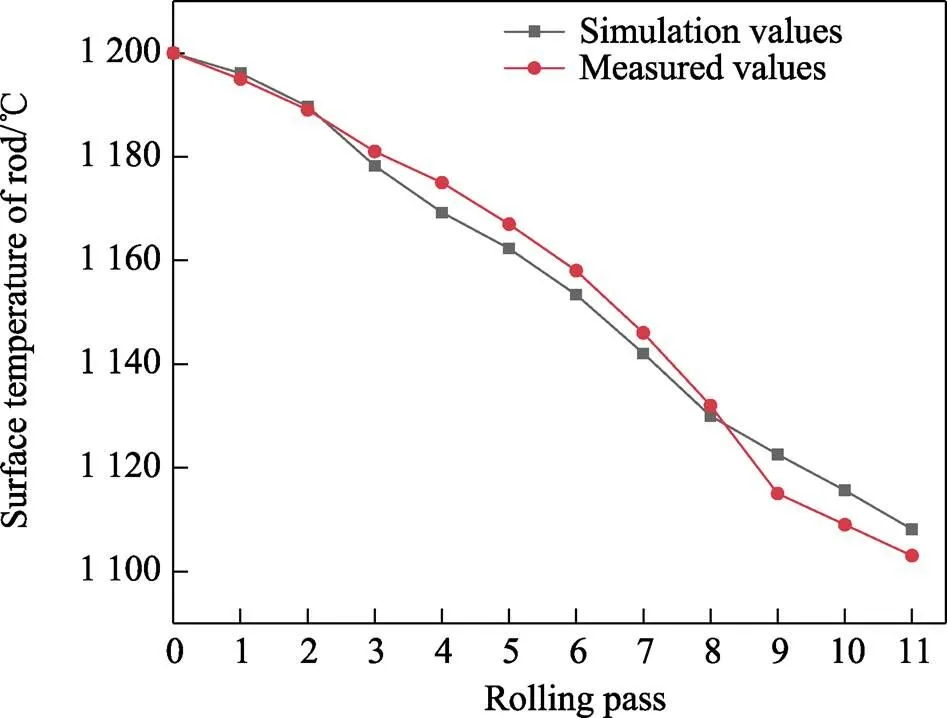
图4 温度模拟值与实测值对比

2.2 轧件出口断面宽度

轧件出口断面宽度能直接验证有限元模拟精度。有限元模拟第1道次（箱形孔型）、第8道次（椭圆孔型）、第11道次（圆孔型）轧件出口断面应力分布如图5所示，可以观察到轧件在不同孔型中塑性变形均匀，轧后几何轮廓良好；等效应力表面较大，逐渐渗入中心，能够显著改善铸坯疏松和缩孔等内部缺陷[24]。

表3对比了11道次轧件出口宽度模拟值与实测值，可以看出，模拟宽度最大偏差值为7.46 mm，出现在第7道次，该孔型为箱形孔型与椭圆孔型的过渡孔型；整体模拟偏差均保持在5 mm之内，模拟精度较高。

表3对11道次轧件宽度实际测量值、模拟值及С.И.古布金（С.И.Губкин）模型计算值也进行了对比，可以看出，С.И.古布金计算偏差普遍较高，尤其是第7—10道次，宽展预测偏差均高于10 mm，最大偏差出现在第8道次椭圆孔，其偏差为17.34 mm，说明该模型对于“椭圆-圆”孔型中轧件宽展计算具有局限性，需要进一步修正。

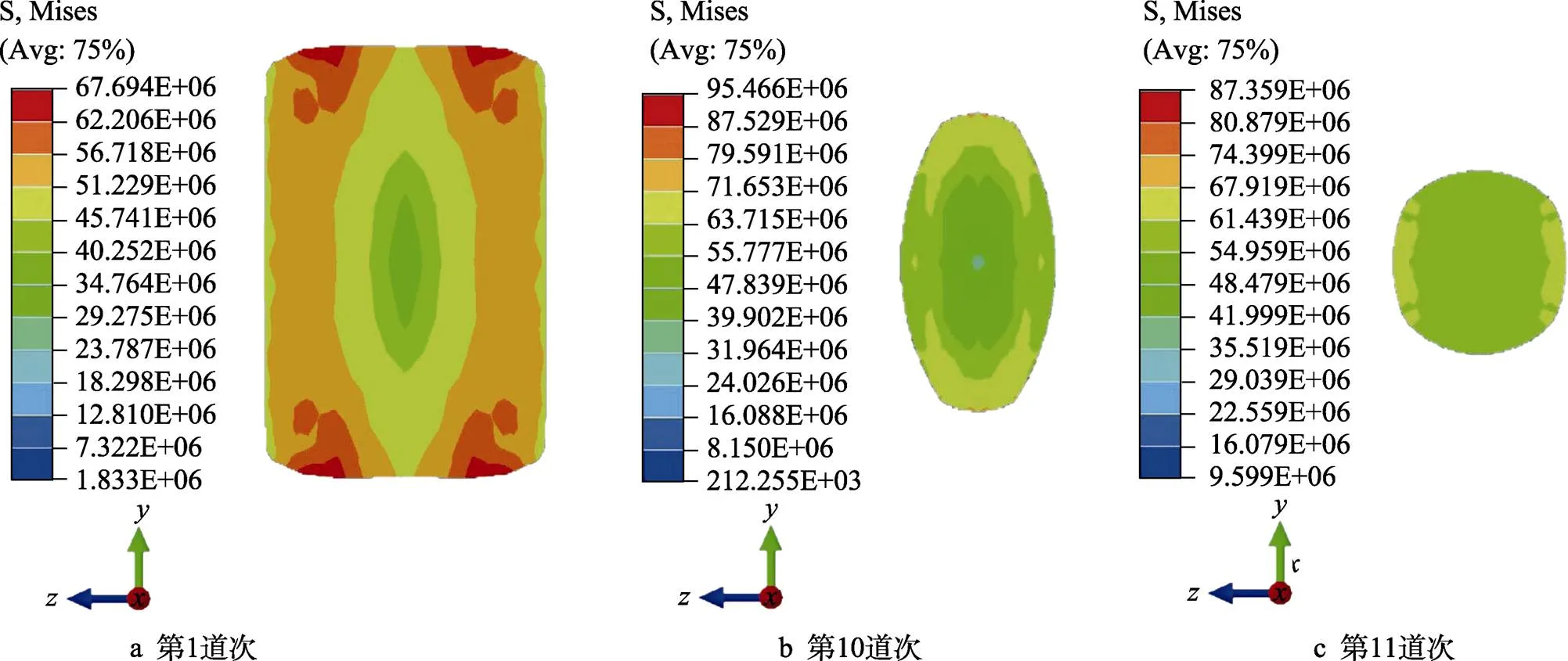
图5 应力分布

表3 轧件各道次宽度对比

Tab.3 Wide comparison of each pass of rolling piece mm

3 宽展模型修正

3.1 形状系数对宽展的影响

根据上述分析，且在实际轧制过程中考虑到“箱形”孔型的压下是均匀的，依照现有的宽展计算公式，可获得和实际偏差较小的结果。但是对于“椭圆-圆”孔型系统，由于接触面为圆弧，沿宽度方向压下不均匀，计算宽展的现有模型没有考虑椭圆圆弧曲率，即椭圆形状对于轧制宽展的影响导致宽展计算精度不高，孔型设计不合理。同时，不同形状系数的椭圆孔型轧出的轧件断面形状亦不同，在下一道次圆孔型中金属流动不同，从而影响轧件质量。

为了深入分析椭圆形状系数对宽展的影响，基于上述第10、11道次孔型，设定椭圆孔型面积一定，为7 112 mm2，椭圆形状系数分别为1.25、1.5、1.75、2.0、2.25、2.5，圆孔型直径为86 mm，构成双道次轧制模型。入口轧件尺寸和轧制温度均参照第9道次出口轧件的数据，其余边界条件设置均与1.2节相同，模拟出口轧件截面如图6所示。各组宽展模拟值如表4所示。

如图6a、b所示，椭圆形状系数为1.25、1.5时，轧后轧件宽度大于孔型宽度，出现“耳子”缺陷，因此，前两组数据不作为参考。如图6c—f所示，随着椭圆形状系数的增大，椭圆孔内轧件的宽度增大，即宽展增加。这是由于压下量增加，变形区长度增加，因而使金属纵向流动阻力增大，根据金属流动最小阻力定律，金属沿横向运动的趋势增大，因而宽展加大。其次，椭圆形状系数增大，则等效轧辊直径增大，同样使变形区长度增加，轧件宽展增大。此外，当椭圆形状系数为2时，椭圆孔型充满度为93.94%；经下一道圆孔型轧后，棒材宽度为86.06 mm，孔型充满度为98.92%，此时“椭圆-圆”孔型轧出的产品尺寸精度高。

3.2 模型修正与试验验证

С.И.古布金宽展公式广泛应用于型钢孔型计算[25]，参数进行等效替代后如式（2）所示。

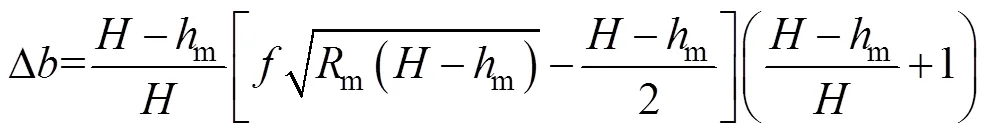
表4 双道次孔型轧制模拟尺寸及充满度

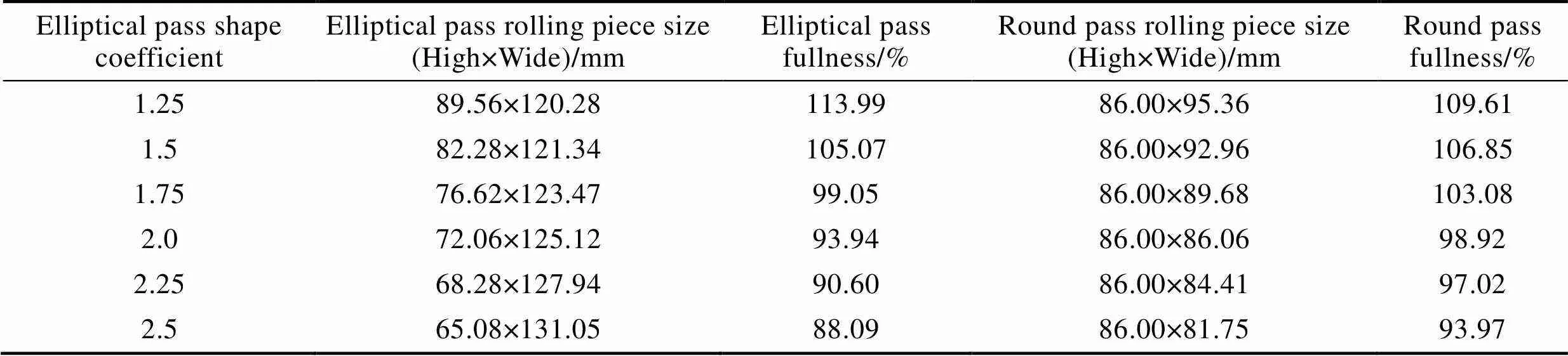
Tab.4 Simulating size and fullness of double-pass rolling

图6 不同椭圆形状系数下双道次孔型出口轧件截面

在式（2）中，m与m都与孔型形状系数直接相关。对有限元模拟宽度值进行数据拟合，孔型充满度与孔型形状系数（1.75～2.5）关系如图7所示。拟合后的模型如式（3）所示，拟合相关度高达99.79%。

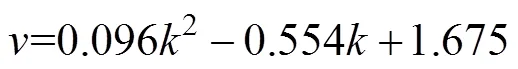
式中：为孔型充满度；为孔型形状系数。

将式（3）、孔型面积、轧辊辊缝代入式（2），构建新型轧制宽展模型，如式（4）所示。

基于某钢厂2209双相不锈钢不同产线，对“椭圆”孔型出口处轧件的截面进行实测，取宽展平均值与理论计算值进行对比，如表5所示。可以看出，修正的宽度预测精度均高于传统计算模型，且计算偏差不超过5%，可用于双相不锈钢产线孔型调整。

表5 轧件宽度对比

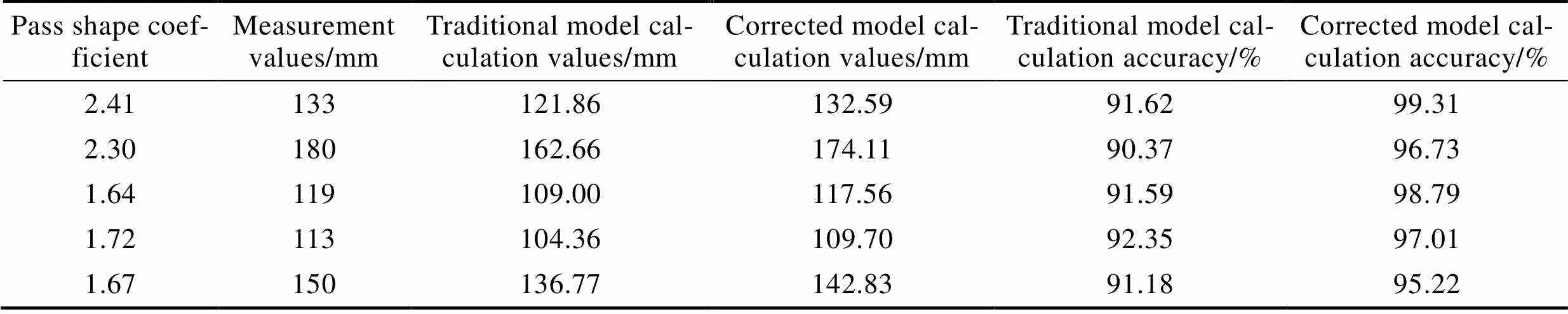
Tab.5 Width comparison of rolling piece

4 结论

1）构建了2209双相不锈钢高温、大塑性变形11道次开坯轧制有限元模型。结果表明，轧件温度模拟值与实测值二者变化趋势基本相同，且受第8和第9道次孔型形状突变的影响，此处被迫出现最大温降。有限元模拟结果显示，11道次后轧件温降约为91.87 ℃，实测温降约为97 ℃，二者相差5.13 ℃，偏差5.29%。

2）构建了不同形状系数的椭圆孔型，并与圆孔型构成双道次轧制。结果表明，随着椭圆形状系数的增大，宽展增大；且当形状系数为2时，椭圆孔型充满度为93.94%，在后一道次圆孔型中充满度最好，达到98.92%。

3）基于С.И.古布金宽展模型，结合孔型形状系数与充满度拟合关系，构建了新型轧制宽展模型，并与实测值进行对比，计算精度高于95%，可用于指导2209双相不锈钢棒材开坯孔型设计及工艺参数优化。

[1] 王青海, 孙世平, 苟复钢, 等.75mm GCr15圆棒材孔型工艺优化及数值模拟[J]. 中国冶金, 2021, 31(8): 77-82.

WANG Qing-hai, SUN Shi-ping, GOU Fu-gang, et al. Process Improvement and Numerical Simulation of75mm round Bar Pass Design[J]. China Metallurgy, 2021, 31(8): 77-82.

[2] 李松松, 李伟, 岳恒全, 等. 合金钢棒材轧制的平均轧辊半径计算模型[J]. 钢铁, 2022, 57(7): 115-124.

LI Song-song, LI Wei, YUE Heng-quan, et al. Analytical Model of Mean Roll Radius in Alloy Steel Bar Rolling[J]. Iron & Steel, 2022, 57(7): 115-124.

[3] AKSENOV S A, CHUMACHENKO E N, LOGASHINA I V, et al. Numerical Simulation in Roll Pass Design for Bar Rolling[J]. Metalurgija, 2015, 54(1): 75-78.

[4] DONG H L, KYONG B L, JAE S L, et al. A New Model for the Prediction of Width Spread in Roughing Mills[J]. Journal of Manufacturing Science and Engineering, 2014, 136(5): 051014.

[5] 余伟, 熊家泽, 雷力齐, 等. 轧制同轴复合棒材的芯材变形规律[J]. 钢铁研究学报, 2016, 28(8): 33-38.

YU Wei, XIONG Jia-ze, LEI Li-qi, et al. Core Rod Deformation Principle of Rolled Coaxial Composite Bar[J]. Journal of Iron and Steel Research, 2016, 28(8): 33-38.

[6] SAKHAEI A H, SALIMI M, KADKHODAEI M. New Multi-Pass Hot Channel Section Rolling Design by the Finite Element Method[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2013, 227(12): 2742-2750.

[7] 谢红飙, 任忠凯, 许秀梅, 等. 棒线材三辊连续减定径机组力能及工艺参数设计[J]. 塑性工程学报, 2017, 24(4): 42-46.

XIE Hong-biao, REN Zhong-kai, XU Xiu-mei, et al. Mechanical and Process Parameters Design of 3-Roll Reducing and Sizing Block for Bar and Wire[J]. Journal of Plasticity Engineering, 2017, 24(4): 42-46.

[8] 常彬彬, 帅美荣, 刘鑫. 棒材三辊孔型自由宽展流动模型[J]. 锻压技术, 2021, 46(11): 207-214.

CHANG Bin-bin, SHUAI Mei-rong, LIU Xin. Flow Model of Free Spread in Three-Roll Passes of Rod[J]. Forging & Stamping Technology, 2021, 46(11): 207-214.

[9] 杨毅. 不锈钢棒材轧制过程的宽展模型及实验研究[D]. 秦皇岛: 燕山大学, 2021: 55-60.

YANG Yi. Widening Model and Experimental Research in the Rolling Process of Stainless Steel Bars[D]. Qinhuangdao: Yanshan University, 2021: 55-60.

[10] 董永刚, 张文志, 宋剑锋. 圆-椭圆-圆孔型中轧制合金钢棒材时宽展迭代模型的建立[J]. 塑性工程学报, 2009, 16(2): 90-95.

DONG Yong-gang, ZHANG Wen-zhi, SONG Jian-feng. Accurate Spread Prediction Model in Alloyed Rod Rolling by Round-Oval-round Pass Sequence[J]. Journal of Plasticity Engineering, 2009, 16(2): 90-95.

[11] ESTEBAN L, ELIZALDE M R, OCAÑA I. Mechanical Characterization and Finite Element Modelling of Lateral Spread in Rolling of Low Carbon Steels[J]. Journal of Materials Processing Technology, 2007, 183(2/3): 390-398.

[12] LAMBIASE F, DI ILIO A. Numerical and Experimental Investigation of Process Parameters Effect of Low Carbon Steel Wire Produced with Roll Drawing Process[J]. Key Engineering Materials, 2011, 473: 113-120.

[13] 周存龙, 吕泽强, 张镭, 等. 棒材DROF工艺粗轧阶段工艺参数对轧件头尾温差的影响[J]. 塑性工程学报, 2021, 28(10): 91-98.

ZHOU Cun-long, LYU Ze-qiang, ZHANG Lei, et al. Effect of DROF Process Parameters of Bar on Temperature Difference between rolling piece Head and Tail during Rough Rolling Stage[J]. Journal of Plasticity Engineering, 2021, 28(10): 91-98.

[14] WANG Hui-hang, GAO Xu-jie, ZHU Guang-ming, et al. Process Analysis and Hole Type Optimization of Micro-Groove Multi-Pass Rolling[J]. The International Journal of Advanced Manufacturing Technology, 2022, 119(3): 2201-2212.

[15] QU Fei-jun, XU Jian-zhong, JIANG Zheng-yi. Finite Element Analysis of Forward Slip in Micro Flexible Rolling of Thin Aluminium Strips[J]. Metals, 2019, 9(10): 1062.

[16] CAI Yan-cheng, WANG Li-ping, ZHOU Feng. Lean Duplex Stainless Steel Tubular Sections Undergoing Web Crippling at Elevated Temperatures[J]. Journal of Constructional Steel Research, 2021, 182: 106681.

[17] GORNYAKOV V, SUN Yong-le, DING Jia-luo, et al. Computationally Efficient Models of High Pressure Rolling for Wire Arc Additively Manufactured Components[J]. Applied Sciences, 2021, 11(1): 402.

[18] 张继祥, 王华, 文辉. 304不锈钢线材椭圆孔型冷连轧过程有限元模拟[J]. 精密成形工程, 2010, 2(1): 15-18.

ZHANG Ji-xiang, WANG Hua, WEN Hui. FEM Simulation on the Two Pass Continuous Cold Rolling of Oval Profile 304 Stainless Steel Wire[J]. Journal of Netshape Forming Engineering, 2010, 2(1): 15-18.

[19] 李明雷, 冼纪元. 大棒材轧制过程温度场的数值模拟分析[J]. 一重技术, 2012(4): 54-56.

LI Ming-lei, XIAN Ji-yuan. Numerical Modeling Analysis of Temperature Field of Bar Rolling Process[J]. CFHI Technology, 2012(4): 54-56.

[20] 李洋, 马立峰, 姜正义, 等. AZ31镁合金中厚板轧制温度场的数值模拟与实验验证[J]. 稀有金属材料与工程, 2019, 48(7): 2185-2192.

LI Yang, MA Li-feng, JIANG Zheng-yi, et al. Numerical Simulation and Experimental Verification of Temperature Field in Medium Plate Rolling of AZ31 Magnesium Alloy[J]. Rare Metal Materials and Engineering, 2019, 48(7): 2185-2192.

[21] BIAN Shou-yuan, ZHANG Xin, LI Sheng-li, et al. Numerical Simulation, Microstructure, Properties of EH40 Ultra-Heavy Plate under Gradient Temperature Rolling[J]. Materials Science and Engineering: A, 2020, 791: 139778.

[22] 周维海, 杜凤山. 热变形过程中氧化铁皮对接触传热及摩擦的影响[C]//制造业与未来中国——2002年中国机械工程学会年会论文集. 北京:中国机械工程学会, 2002: 2506-2510.

ZHOU Wei-hai, DU Feng-shan. Effect of Iron Oxide on Contact Heat Transfer and Friction during Thermal Deformation[C]// Manufacturing and Future China - Proceedings of 2002 Annual meeting of China Mechanical Engineering Society. Beijing: Chinese Society of Mechanical Engineering, 2002: 2506-2510.

[23] 胡韬, 岳晓丽, 陈慧敏. P110石油管用钢坯热轧工艺数值模拟[J]. 锻压技术, 2016, 41(11): 153-157.

HU Tao, YUE Xiao-li, CHEN Hui-min. Numerical Simulation on Steel Billet of Oil Well Pipe P110 in Hot Rolling[J]. Forging & Stamping Technology, 2016, 41(11): 153-157.

[24] 宫美娜, 李海军, 王斌, 等. Nb-Ti连铸坯热芯大压下轧制动态再结晶行为研究[J]. 轧钢, 2020, 37(1): 12-17.

GONG Mei-na, LI Hai-jun, WANG Bin, et al. Study on Dynamic Recrystallization in Nb-Ti Microalloyed Slab during Hot-Core Heavy Reduction Rolling[J]. Steel Rolling, 2020, 37(1): 12-17.

[25] 武大鹏, 陈文琳, 张文超, 等. 矩形钢丝成形有限元模拟及工艺参数优化[J]. 金属制品, 2010, 36(1): 36-41.

WU Da-peng, CHEN Wen-lin, ZHANG Wen-chao, et al. Finite-Element Simulation of Rectangular Wire Shape and Optimization of Process Parameters[J]. Metal Products, 2010, 36(1): 36-41

Spreading Model of Duplex Stainless Steel Bar Based on the Shape Coefficient of Pass

LI Liang1, SHUAI Mei-rong1, TIAN Heng-guang1, WANG Jian-mei1, WANG Hui-mian2

(1. Engineering Research Center of Ministry of Heavy Machinery, Taiyuan University of Science and Technology, Taiyuan 030024, China; 2. Shanxi Taigang Stainless Steel Co., Ltd., Baowu Group, Taiyuan 030003, China)

The work aims to establish an "elliptical" hole shape coefficient based spreading model to solve the problems 2209 duplex stainless steel bar in the blank rolling stage, such as low calculation accuracy, unreasonable hole design, easy to produce "folding", "ear" and other surface defects, to improve the dimensional accuracy of product. By means of the finite element model of 11-pass billet rolling process of 2209 duplex stainless steel, the effects of temperature distribution of rolling pieces and different shape coefficients of elliptic pass on the width of rolling pieces was studied. The traditional C.И.Губкин calculation model was modified and compared with the measured data to verify the reliability of the modified model. The results showed that in the simulated rolling process, the temperature change trend of the rolling piece was basically the same as the measured value, and the temperature dropped by 91.87 ℃ after 11 passes, along with the decrease was large in the hole mutation stage. By comparing the size data of each roll, it was concluded that the calculation deviation of the C.И.Губкин model was large, and the deviation of the elliptical hole was the largest in the 8th pass. After simulated rolling of elliptical pass with different shape coefficients, it was found that the fullness of elliptical hole was 93.94% and the fullness of next round hole was 98.92% when the shape coefficient was 2, and the product size precision was high. The corrected spreading model is compared with the measured values with a calculation accuracy of higher than 95%. The modified shape coefficient model improves the calculation accuracy of rolling width and can be used to guide the hole design and optimization of duplex stainless steel billet rolling.

duplex stainless steel; billet rolling; numerical simulation; shape coefficient; spreading model

10.3969/j.issn.1674-6457.2023.02.010

TG306

A

1674-6457(2023)02-0078-08

2022‒04‒29

2022-04-29

山西省重点研发计划（201903D121043）；山西省先进钢铁材料重点科技创新平台建设项目（20201041）；常州市领军型创新人才引进培育项目（CQ20200042）；山西省研究生教育改革研究课题（2020YJJG241）；山西省研究生教育创新项目（2022Y709）

Shanxi Province Key Research and Development Plan Project (201903D121043); Advanced Steel Materials Key Science and Technology Innovation Platform Construction Project of Shanxi Province (2020201041); Changzhou Leading Innovative Talents Introduction and Cultivation Project (CQ20200042); Shanxi Graduate Education Reform Research Project (2020YJJG241); Shanxi Graduate Education Innovation Project (2022Y709)

李亮（1997—），男，硕士生，主要研究方向为双相不锈钢热变形机理及关键技术。

LI Liang (1997-), Male, Postgraduate, Research focus: thermal deformation mechanism and key technology of duplex stainless steel.

帅美荣（1978—），女，博士，教授，主要研究方向为金属塑性变形理论与技术。

SHUAI Mei-rong (1978-), Female, Doctor, Professor, Research focus: metal plastic deformation theory and technology.

李亮, 帅美荣, 田恒光, 等. 基于孔型形状系数的双相不锈钢棒材宽展模型研究[J]. 精密成形工程, 2023, 15(2): 78-85.

LI Liang, SHUAI Mei-rong, TIAN Heng-guang, et al. Spreading Model of Duplex Stainless Steel Bar Based on the Shape Coefficient of Pass[J]. Journal of Netshape Forming Engineering, 2023, 15(2): 78-85.