计及综合需求响应参与消纳受阻新能源的多时间尺度优化调度策略

张尧翔, 刘文颖，庞清仑，李亚楼，安宁，李芳

(1. 新能源电力系统国家重点实验室(华北电力大学)，北京市 102206；2.中国电力科学研究院有限公司，北京市 100192)

0 引 言

为促进能源可持续供应，提高新能源发电占比成为世界各国电网发展的共同愿景。近年来，我国新能源发电装机实现了跨越式增长，截至2021年，我国风光电装机容量为63 504万kW，为2010年装机的21倍，构建适应新能源占比逐渐提高的新型电力系统成为我国电力行业的重要发展战略[1-2]。而随着大规模新能源的并网，新能源发电的不确定性及反调峰特性提高了系统的新能源消纳压力[3]。与此同时，源侧大规模新能源替代火电，导致系统源侧调节能力匮乏，严重制约了新能源电能的消纳。灵活性资源不足成为了制约新型电力系统发展的主要瓶颈。

近年来，随着多能转换技术的发展，各类能源网络间的耦合程度不断提高，综合能源系统(integrated energy system，IES)迅速发展，利用IES不同能源网络的灵活响应资源，进行综合需求响应(integrated demand response, IDR)，是提高新型电力系统新能源消纳能力的有效手段[4]。

目前国内外学者在IDR消纳新能源方面已有一定的研究，文献[5]对综合能源系统中的冷、热负荷需求响应机理进行分析，并建立了冷、热负荷需求响应模型，从机理上证明了综合需求响应消纳新能源的可行性。文献[6]基于热电耦合原理，考虑负荷侧电热负荷响应弹性及系统功能方式多样性，提出了电热负荷响应补偿机制。文献[7]针对园区IES需求响应，建立了系统运营商与负荷聚合商主从博弈交易模型，提出了多主体下的IES多能交易优化方法。上述文献对冷热电负荷参与新能源消纳的响应机理及模型进行了分析，但均是在负荷及新能源精确预测的前提下进行，未考虑源荷不确定性对模型优化调度的影响。

在多类型负荷需求响应过程中，针对不确定性因素，可借鉴电力系统中处理不确定性的多时间尺度滚动调度基本思想，将IES调度过程分为多个阶段，各阶段在不同时间尺度下相互配合，逐级削弱不确定性因素对优化调度的影响。文献[8]针对风光不确定性，基于多场景随机规划和模型预测控制方法，建立冷热电联供系统多时间尺度协调优化模型。文献[9]考虑源荷不确定性及储能设备配置对综合能源系统IES优化调度的影响，分别建立了日前、日内滚动和实时反馈3个时间尺度的优化调度模型。文献[10]构建了含储热、热电联产的综合电热系统需求响应模型，并提出了新能源消纳日前日内两阶段调度方法。文献[8-10]通过多时间尺度滚动方法，减少源荷不确定对系统优化的影响，但未能深入考虑需求侧资源对IES优化的影响。

针对上述问题，本文提出计及综合需求响应参与消纳受阻新能源的多时间尺度优化调度策略。首先，建立IES能量耦合模型及冷、热、电负荷多类型需求响应模型。其次，在日前时间尺度，基于主从博弈理论，建立价格型IDR博弈优化调度模型；在日内时间尺度，针对新能源出力不确定性，建立考虑激励型IDR的日内多能优化调度模型。最后，通过仿真验证本文所提方法的有效性。

1 IES结构及需求侧响应策略

1.1 IES结构

典型IES结构如图1所示，主要包括能源输入、多能转换、多类型负荷需求三部分。能源输入主要包括风电机组、光伏机组、外部电网、输气管道；多能转换中的设备主要包括电锅炉(electric boiler，EB)、燃气锅炉(gas boiler, GB)、电制冷设备(air conditioner, AC)、冷热电联供设备(combined cooling, heating and power, CCHP)；多能负荷需求包括冷负荷需求、热负荷需求及电负荷需求。

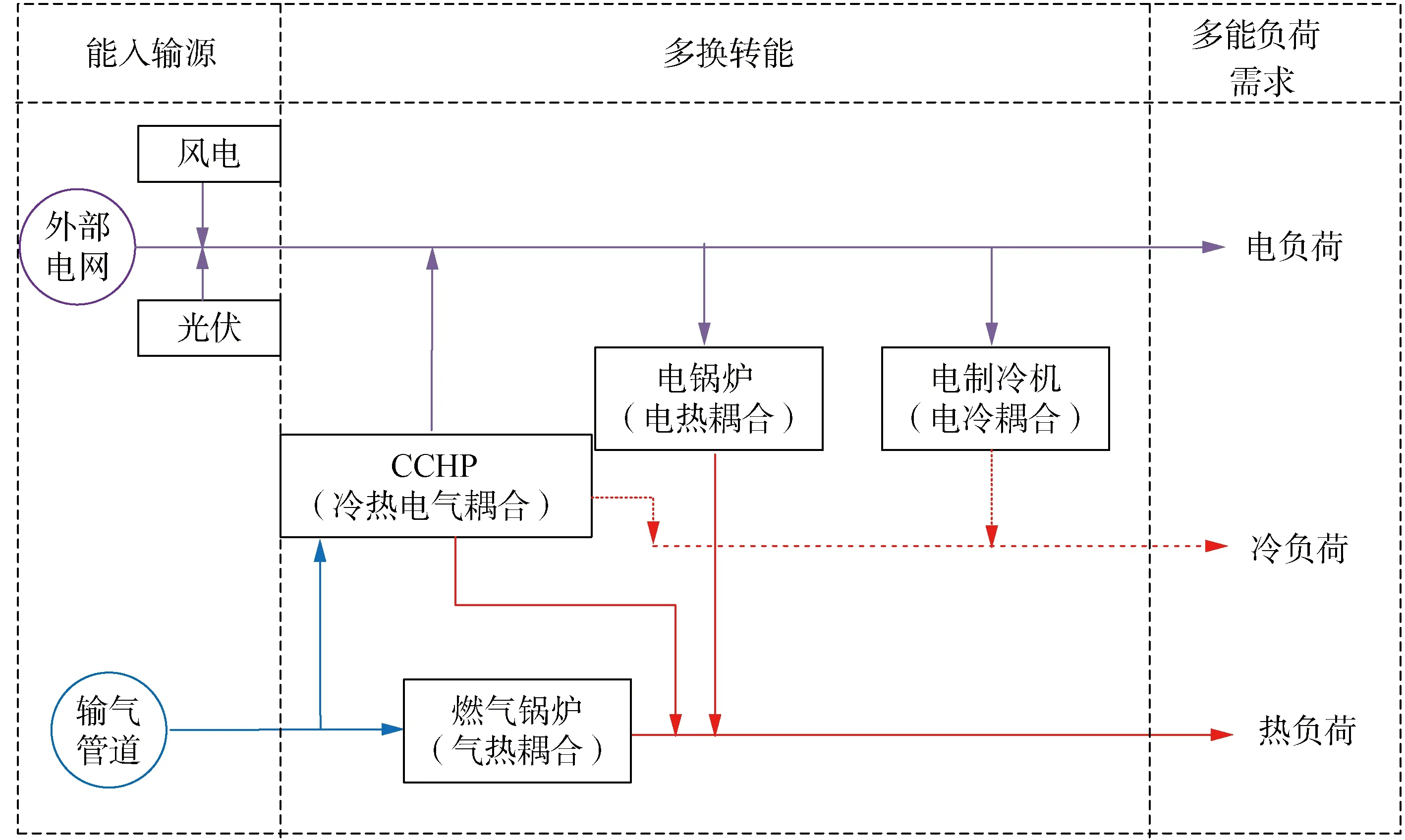
图1 IES结构图Fig.1 IES Structure Diagram

针对典型IES结构分析，基于能量枢纽理论[11]，建立图1所述的IES能量转换模型：

L=H×P

(1)

(2)

(3)

(4)

其中，能源输入侧的分配因子满足等式关系：

(5)

1.2 冷热电负荷需求响应策略

在IES中，存在冷热电负荷需求，均可进行负荷需求响应管理。其中，按响应方式的不同将电负荷需求响应分为价格型需求响应及激励型需求响应。考虑IES中多能耦合及转换特点，冷热负荷通过替代响应的方式参与负荷需求侧管理[12]。

1.2.1价格型电负荷需求响应

价格型需求响应指电网通过对负荷电价调整，影响负荷用能行为，以满足电网的调峰需求。在经济学中，常采用价格弹性矩阵建立电负荷价格需求响应模型，价格弹性系数计算公式如下：

(6)

考虑负荷本时刻电价变化“自响应”及其余时刻电价变化“互响应”[13]，得到时段1—t内电负荷电价需求响应模型：

(7)

基于式(7)得到t时段电负荷参与电价需求响应后负荷功率：

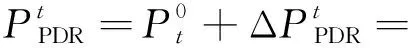
(8)

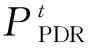
由于在日时间尺度内的市场交易中，气价通常为固定值，因此本文主要考虑电价变化导致的价格型需求响应，不考虑气价变化。

1.2.2激励型电负荷需求响应

激励型负荷响应指用户与供电公司提前签订合约，电网根据电负荷变化量支付经济补偿[14-15]。本文所讨论负荷激励响应为可中断响应，采用分段报价形式进行，如图2所示。

图2 激励型IDR分段报价曲线Fig.2 Segmented quotation curve of Incentive IDR

其数学表达式如下：

(9)

(10)

(11)

1.2.3替代型冷热负荷需求响应

在IES系统中，通过各类型的耦合设备，可实现能源的互换。能源间的转换满足能量守恒定理，基于此，建立冷热负荷替代型需求响应模型：

(12)

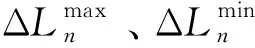
参与替代响应后负荷Ln可由下式计算得到：

(13)

参与替代响应后，各类型负荷变化量需满足能量转换平衡约束：

(14)

1.3 不同时间尺度下需求响应分类

由1.2节可知，价格型需求响应需要考虑不同时段电价对负荷变化量的互响应影响，多用于日前整体优化。激励型需求响应可根据具体的电网需求直接进行负荷调整，可进行日内短时间尺度优化。因此，在不同时间尺度下，采用不同的需求侧响应方式，以最大程度地利用IES需求侧响应资源，促进新能源消纳。表1为不同时间尺度下IDR分类。

表1 不同时间尺度下IDR分类Table 1 IDR classification at different time scales

在日前时间尺度，提出价格型IDR控制策略，通过电价调整，激励多类型负荷参与消纳日前受阻新能源。在日内时间尺度，考虑新能源预测不确定性，提出激励型IDR策略，充分挖掘负荷调节潜力，对日内偏差新能源进行消纳。其中电负荷可直接参与日前及日内需求响应，冷热负荷则通过替代响应的方式参与。

2 IES多时间尺度调度策略

2.1 控制思路

本文所提多时间尺度调度模型包括日前及日内两个时间尺度下的优化调度，调度思路如图3所示。

图3 IES多时间尺度IDR调度思路Fig.3 Multi-Time Scale IDR Scheduling Ideas for IES

日前优化阶段：控制时间尺度为1 h，通过价格型IDR，对日前受阻新能源进行消纳。具体地，基于主从博弈理论，对系统运营商与综合能源用户间进行量价博弈。

系统运营商考虑弃风弃光惩罚系数及冷热负荷舒适度成本，以自身收益最大为目标制定电价策略，发送至综合能源用户。用户基于系统提供的电价信息，以自身用能成本最小为目标，调整用能策略，并传回系统运营商。通过反复迭代，直至达到博弈均衡，得到双边共赢的系统电价及需求响应量。主从博弈框架如图4所示。

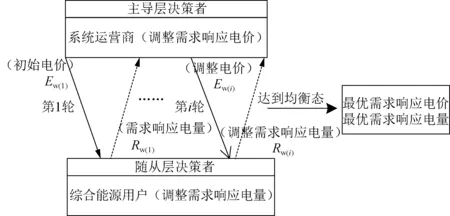
图4 日前主从博弈框架Fig.4 Framework of master-slave game

日内滚动调整阶段：控制时间尺度为15 min，预测时域为4 h。利用激励型IDR，通过滚动优化的方式，对日内新能源预测正误差造成的盈余新能源进行消纳。具体地，在t时刻，基于新能源日内预测，以日内设备调整成本、购能成本最小为目标，对预测时域内的IES设备出力及激励型IDR响应功率进行优化，并执行第一个时段的控制计划。在t+1时段，对下一个预测时域内的新能源预测出力进行更新，重复上述步骤进行滚动优化。

2.2 考虑价格型IDR日前主从博弈优化调度

2.2.1系统运营商模型

系统运营商基于综合能源用户需求响应策略，以净利润最大为目标，确定自身电价策略：

maxFS=Csale-CND-CNF

(15)

(16)

(17)

(18)

模型约束包括电价约束及新能源功率约束：

(19)

式中：Rmax、Rmin分别为系统运营商可提供的电价上、下限。

2.2.2综合能源用户模型

考虑冷、热负荷调整会造成温度变化，舒适度降低的特点，引入舒适度成本，用以衡量冷、热负荷变化对用户的影响[12]。综合能源用户以自身购能成本及舒适度成本最小为目标：

minFuser=Cbuy+Csat

(20)

(21)

(22)

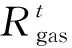
综合能源用户电价需求响应量满足多能枢纽转换等式约束及负荷需求响应约束：

(23)

2.2.3主从博弈模型

系统运营商与综合能源用户在日前交易过程中，双方分别以自身收益及成本为目标进行博弈，其中系统运营商目标是确定一个最优的系统电价，激励综合能源用户进行电价需求响应，实现自身收益最大；综合能源用户基于系统电价，确定自身需求响应电量，最大化降低自身用能成本。

(24)

式中：“*”代表最优策略对应的值，下同。

(25)

2.2.4均衡解唯一性证明

当主从博弈双方的策略空间满足非空有界下凸闭子集，且效用函数为策略空间内的连续凸函数，则该主从博弈存在Stackelberg均衡，且均衡解唯一[16]。

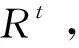
(26)

Fuser分别关于决策变量的二阶偏导数始终大于等于0，因此该主从博弈均衡解存在且唯一。

2.2.5主从博弈求解方法

根据式(15)、(20)可知，系统运营商计算其利润时，受到综合能源用户电价需求响应量影响，而综合能源用户计算其相应成本时，需要系统提供电价参数，两个模型求解互相影响，因此本文采用分布式优化算法对主从博弈模型进行求解[17]。同时，鉴于综合能源用户目标函数为二次函数，在分布式计算过程中调用Gurobi工具箱进行求解，以提高模型求解精度和速度。模型求解流程如附录图A1所示。

2.3 考虑激励型IDR日内滚动优化调度

2.3.1 目标函数

针对新能源预测正误差造成的日内新能源盈余，对综合能源用户进行激励型IDR。激励型IDR响应策略是系统运营商与用户签订合同，根据合同确定可削减的负荷电量、补偿价格等。以日内综合能源用户净收益最大为目标：

maxFSI=EIDR-CE-grid-CIES

(27)

(28)

(29)

(30)

2.3.2 约束条件

日内调度阶段需满足式(23)中的多能转换约束及激励需求响应能力约束：

(31)

式中：PIDRmax为单位时间内激励需求响应最大功率。

3 算例分析

3.1 算例概述

为验证本文所提方法的有效性，以图1所示算例为例进行仿真验证。日前用户的冷、热、电负荷预测出力及风光电预测信息如附录图A2所示，IES向电网购电价如附录表A1所示，购气价为3.24 元/m3。IES中各能源耦合设备参数如附录表A2所示。用户对冷、热负荷的舒适度系数分别为0.008、0.016[18]，弃风弃光惩罚系数分别为0.45 、0.35 元/(kW·h)。风电日前预测误差服从均值为0.107、标准差为0.451的正态分布，光伏日前预测误差服从均值为0.842、标准差为12.690的正态分布[19]。电价自弹性系数为-0.21，互弹性系数为0.032；日内电负荷单位时间内激励需求响应最大功率为30 kW/15 min，各级激励响应补贴价格如附录表A3所示；电负荷最大削减和增加比例为0.5，冷热负荷最大削减和增加比例为0.4。

3.2 日前优化调度结果分析

为验证本文所提的考虑价格型及替代型IDR日前主从博弈优化调度策略的有效性，设置两种日前优化调度方案。方案1：不考虑IDR，以综合能源系统日前购能成本最低为目标进行优化调度；方案2：本文所提考虑价格型及替代型IDR主从博弈日前优化调度。

方案2采用主从博弈的方式，对日前新能源受阻时段的系统电价及需求响应电量进行博弈求解，以新能源受阻时段02：00—03：00为例对博弈过程进行介绍，博弈结果如表2所示。

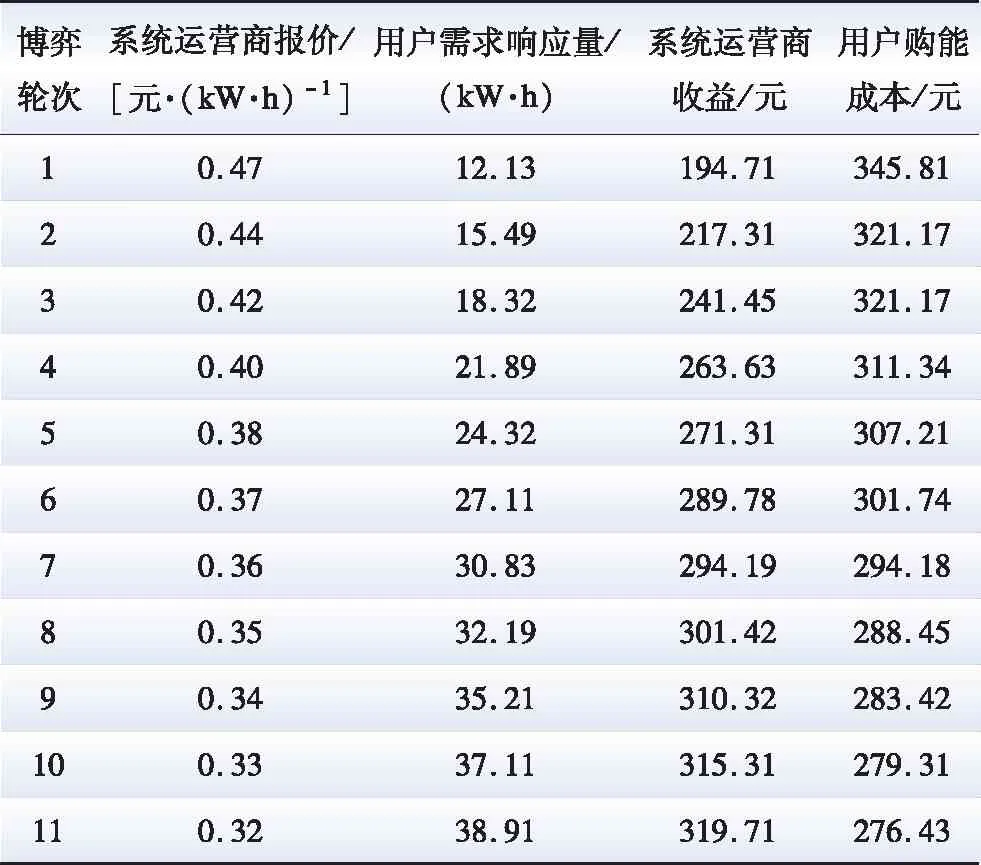
表2 02：00—03：00各系统运营商与综合能源用户博弈决策结果Table 2 Decision results of the game between each system operator and integrated energy users in 2:00-3:00

由表2可知，在交易时段02：00—03：00，系统运营商与综合能源用户经过11轮博弈，达到主从博弈均衡状态，均衡状态下的系统运营商提供交易电价为0.32 元/(kW·h)，综合能源用户可提供的需求响应电量为38.91 kW·h。基于此，进一步得到方案2其余新能源受阻时段交易结果。

两种方案下电价变化、新能源受阻功率分别如图5、6所示。方案2下冷热电负荷电价需求响应量如图7所示。

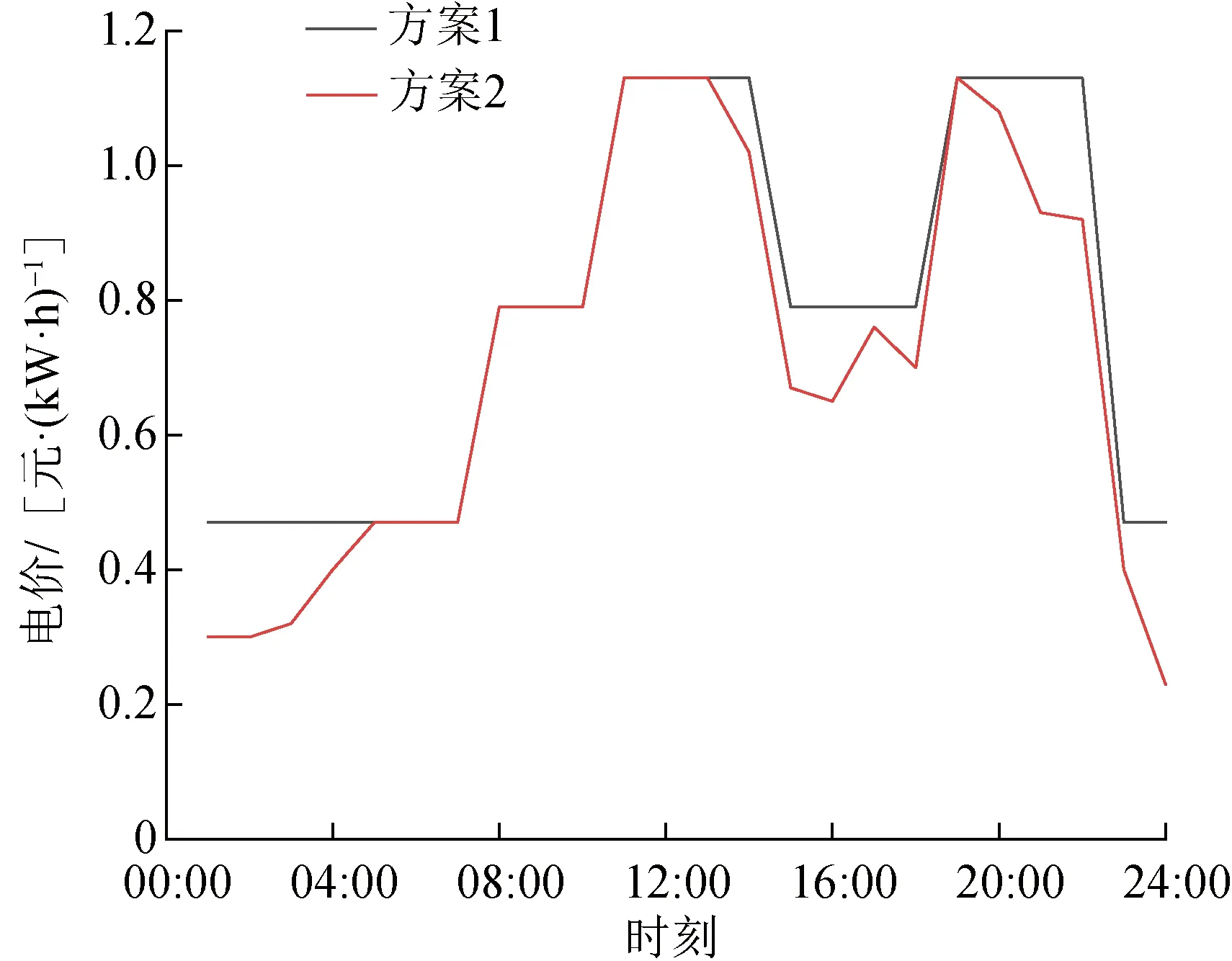
图5 不同方案下的系统电价Fig.5 System electricity price under different schemes

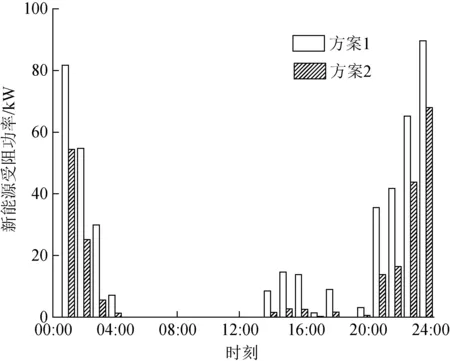
图6 不同方案下的新能源受阻功率Fig.6 New energy blocked power under different schemes

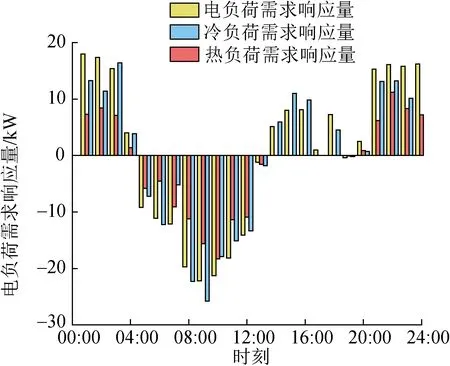
图7 冷热电负荷日前需求响应量Fig.7 Day-ahead demand response of cooling, heating and power loads

由图5—7可知，由于夜间时段风电大发，负荷需求低，因此新能源受阻时段主要分布在夜间时段。相较于方案1固定电价，方案2通过主从博弈的方式，在初始电价基础上，对新能源受阻时段的电价进行补贴，通过降低新能源受阻时段电价的形式，激励综合能源用户进行电价需求响应，增加夜间新能源受阻时段的负荷需求，促进新能源日前消纳。其中，由于冷、热负荷调整会产生舒适度成本，且热负荷调整成本系数高于冷负荷，因此在夜间新能源受阻时段，电负荷优先参与需求响应，其次是冷负荷，当电、冷负荷响应能力不足时，热负荷参与响应。

两种方案下日前优化结果如表2所示，由表2可知，通过采用价格型及替代型IDR，新能源消纳量增加了217.94 kW·h，系统运营商净利润增加了947.14 元。在综合能源系统负荷侧，参加价格型及替代型IDR虽然增加了需求响应成本，但由于系统电价降低，减少了其购能成本，总体效益增加。结果表明，在日前时间尺度，通过采用本文所提的考虑价格型及替代型IDR日前主从博弈优化调度策略，在促进新能源消纳的同时，实现系统运营商及用户的收益增加。

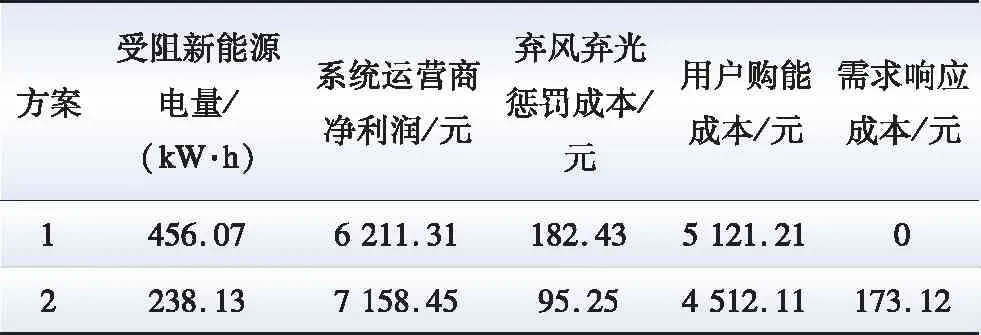
表3 日前不同方案下优化结果Table 3 Day-ahead optimization results under different schemes

3.3 日内优化调度结果分析

为验证日内激励型IDR策略的有效性，本节在3.2节日前考虑价格型及替代型IDR的基础上，设置两种日内优化调度方案。方案3：在日内调度中采用滚动优化，不考虑激励型IDR；方案4：在日内滚动优化基础上，考虑激励型IDR参与。

两种方案下新能源日内受阻功率、负荷需求变化如图8、9所示。由图8可知，方案3下的新能源受阻时段为夜间00:00—03:45、19:15—23:45及日间12:15—16:00时段；方案4下的新能源受阻时段为夜间00:00—01:45、19:15—23:45。针对新能源预测误差造成的日内受阻新能源，相较于方案3，方案4通过激励型IDR策略，激励用户在新能源受阻时段调整负荷需求。具体地，针对日间12:15—16:00小规模新能源受阻电量，为减少多能耦合设备的调整成本，由电负荷用户单独参与需求响应，完成对日间受阻新能源的全额消纳；针对夜间00:00—03:45、19:15—23:45大规模的受阻新能源，单独电负荷难以完全消纳，由冷热电负荷共同参与需求响应，减少了夜间受阻新能源规模。

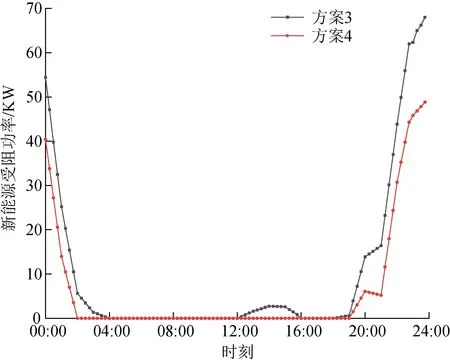
图8 日内不同方案下新能源受阻功率Fig.8 Blocked power of new energy under different schemes intra-day

图9 日内不同方案下负荷需求变化Fig.9 Intra-day power load demand under different scenarios

日内两种方案下的日内优化结果如表4所示，相较于方案3，方案4利用激励型IDR，减少了受阻新能源电量136.01 kW·h。在用户侧，由于多能负荷参与激励需求响应，增加了用户需求响应收益，弥补了负荷调整带来的耦合设备出力调整惩罚成本升高，总体的效益增加，提高了用户参与日内IDR的积极性。

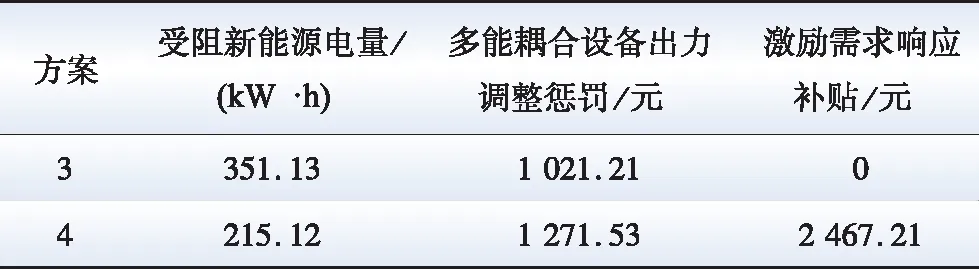
表4 日内不同方案下优化结果Table 4 Intra-day optimization results under different schemes

4 结 论

为促进新能源消纳，本文提出了一种计及综合需求响应参与消纳受阻新能源的多时间尺度优化调度策略，在日前、日内两个时间尺度下，利用不同类型IDR策略提高新能源消纳能力。通过仿真算例，验证所提策略的有效性，并得出以下结论：

1)在日前时间尺度，采用基于主从博弈的价格型IDR策略，通过综合能源用户与系统运营商间量价博弈，制定符合双方利益最大化的交易电价，提升了用户参与需求响应的积极性，达到促进新能源消纳的目的。

2)在日内时间尺度，针对新能源预测误差造成日内盈余新能源，通过滚动优化方式，利用激励型IDR策略，进一步挖掘负荷需求响应潜力，减少了日内新能源受阻电量。