基于议价能力的风-光-CHP多主体优化运行策略

解瑞硕，于泽旭，窦震海，乔萌萌，赵晔，王媛媛

(山东理工大学电气与电子工程学院，山东省淄博市 255000)

0 引 言

如今，煤炭、石油等化石能源濒临枯竭导致的能源危机及其使用后造成的温室效应等问题，阻碍着人类社会的生存和发展。大规模发展可再生能源如太阳能和风能，是解决上述问题的有效措施[1-4]。但由于可再生能源的波动性和间歇性，风电场或光伏电站的大规模并网将严重影响电力系统的稳定运行，因此可再生能源大规模平稳消纳仍是一个亟待解决的问题。多能耦合综合能源系统概念的提出，为可再生能源的消纳提供了一条新途径。首先，在综合能源系统中，利用负荷需求与可再生能源出力的不同时性，使得可再生能源通过能量转换装置(如电转气装置、热泵)转换为其他形式的能源(如天然气、热能)来满足相应的负荷需求[5-6]；其次，碳交易机制及碳交易市场的日益成熟，综合能源系统若直接或间接地使用化石能源会产生高昂的碳排放成本，促使其消纳部分可再生能源[7-8]。针对综合能源系统的可再生能源消纳和碳排放方面，大多数学者采用集中式求解方法，将综合能源系统视为一个利益持有者，实现其整体的低碳性或经济性提高。例如，文献[7]在综合能源系统中构建了考虑阶梯式碳交易机制和电转气两阶段运行过程的运行策略，改善了可再生能源的消纳量和综合能源系统的低碳性。文献[8]建立了以综合能源系统的投资成本、运行成本和碳交易成本之和最小为目标的规划模型，并验证了该规划模型在系统低碳性和经济性方面的有效性。但上述文献的运行策略均忽略了目前传统的集中式综合能源系统正在向职能不同的分布式多主体能源系统转变的趋势，集中式求解方式已不适用于如今的电力市场环境。综合能源系统中风电主体、光伏主体的可再生能源供能侧和热电联产主体的能源需求侧均属于不同利益的主体，都具有个体理性和利益需求。如何处理主体之间的利益关系成为彼此合作的关键。

博弈论中的合作博弈和非合作博弈是处理分布式多主体复杂利益关系的有效方法。非合作博弈强调个体之间进行自主决策即个体理性，与策略环境中其他参与主体无关，不易产生纳什均衡解。而合作博弈兼顾个体理性和整体理性的统一，通常可实现全局最优解或帕累托最优解[9-10]。基于合作博弈理论处理多主体复杂利益关系的有效方法通常有2种：Shapley值法[11-12]和纳什议价[13-14]。文献[11]利用Shapley值法按各微电网主体对系统边际贡献进行涌现收益再分配，有效解决了联盟成员涌现收益分配不公平的问题。文献[12]提出了以含电转气的综合能源联盟净收益最大为目标的系统运行模型，并基于Shapley值对联盟的每个主体进行了公平、合理的利润分配。文献[13]基于纳什谈判理论建立了基于电能互济的区域综合能源系统运行优化模型，在最小化系统运行成本的同时，并保证了联盟参与者之间利益公平分配。文献[14]基于纳什议价理论提出了一种风-氢-热多主体能源系统的合作规划与运行模型，提出的合作模型能够显著提高各参与者和合作联盟的利益。然而，Shapley值法复杂度随着系统内主体数量的增多而上升，随着电力市场不断推进，主体数量将不断增多，其应用场景将受到一定的限制，并且会造成维数灾[15]。纳什议价理论克服了Shapley值法的缺点，其应用难度不会随着主体数量出现明显变化，因而适用于多主体利润分配问题[16]。但是标准纳什谈判模型中，每个参与主体获得相等的利益分配数额，未考虑合作后利益公平分配的问题。由于参与主体在投资成本和效益评价指标等方面存在较大的差异，若合作后获得利益分配金额相同，则不利于合作的继续进行。

为解决上述问题，本文将综合能源系统划分为风电主体、光伏主体和热电联产(combined heat and power，CHP)主体，建立风-光-CHP多主体纳什谈判模型，将其分解为系统运行成本最小化问题(P1)和交易支付问题(P2)；在P2中，提出考虑经济和环境增幅的议价能力模型，各主体根据自身议价能力来实现收益的公平分配。其次，在CHP主体中引入电制氢技术和阶梯型碳交易机制，探究电制氢技术相对于电转天然气技术存在的优势。最后，采用交替方向乘子法(alternating direction method of multipliers，ADMM)[16]对所提模型求解，保证参与主体的隐私。

1 风-光-CHP合作运行模型

风电主体、光伏主体和CHP主体的运行框架如图1所示。风电主体、光伏主体和CHP主体均与电网相连，电网与其进行电能交易，也可为主体之间的分布式能源交易提供基础设施服务，并收取相应的过网费用[17]。在非合作运行策略下，风电主体和光伏主体只与电网进行电能交易，若上网电量超出联络线传输功率，会造成弃风、弃光现象；在合作运行策略下，风电主体和光伏主体在可再生能源上网电价比工业电价低的时段选择与CHP主体进行电能交易；而CHP主体需要同时考虑购电成本和碳排放成本，来选择合适的交易策略。

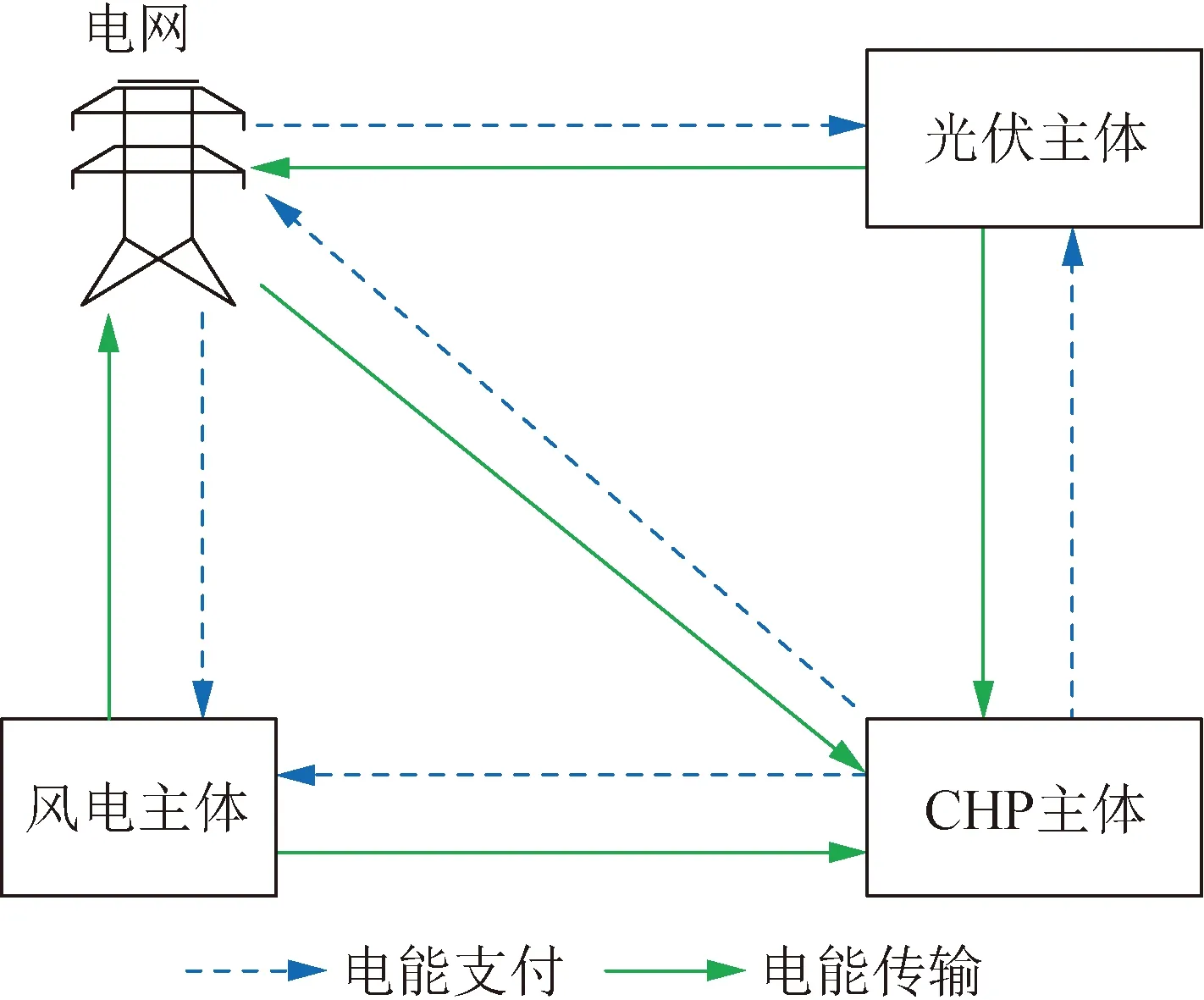
图1 风-光-CHP多主体运行框架Fig.1 Wind-solar-CHP multi-agent operation frame

1.1 风电主体合作运行模型

风电主体的年化投资成本为：

(1)

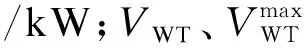
风电主体向CHP主体的售电收益以及向电网的售电收益分别为：

(2)

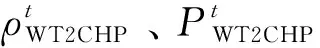
分布式电能交易时，电网收取风电主体的过网费用为：

(3)

式中：ψWT、φWT为风电过网费折算系数。

综上，风电主体的目标函数表示为：

(4)

风电主体的运行约束条件包括：功率平衡约束、决策变量非负约束和风电上网波动性约束。

(5)

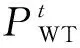
1.2 光伏主体合作运行模型

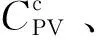
光伏主体的年化投资成本为：

(6)

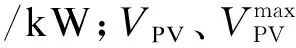
光伏主体向CHP主体的售电收益和向电网的售电收益为：

(7)

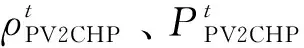
分布式电能交易时，电网收取光伏主体的过网费用为：

(8)

式中：ψPV、φPV为光伏过网费折算系数。

综上，光伏主体的目标函数表示为：

(9)

光伏主体的运行约束条件包括：功率平衡约束、决策变量非负约束和光伏上网波动性约束。

(10)

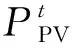
1.3 CHP主体合作运行模型

CHP主体能量流动框架如图2所示。风电主体和光伏主体向CHP主体提供清洁电能，既促进了可再生能源的消纳，又降低了CHP机组的碳排放成本和用电成本；电解槽(electrolysis cell，EL)将盈余可再生能源发电和电价谷时的电能转化为氢气；氢气直接供给氢燃料电池(hydrogen fuel cell，HFC)进行热电联产满足电负荷和热负荷，也可经由甲烷反应器(methane reactor，MR)进一步转化为天然气；CHP机组燃烧天然气同时满足电、热负荷需求；各设备运行过程产生的碳排放最终通过碳交易市场进行交易。碳配额模型和阶梯型碳交易模型见文献[4]，下文不再对其进行建模。

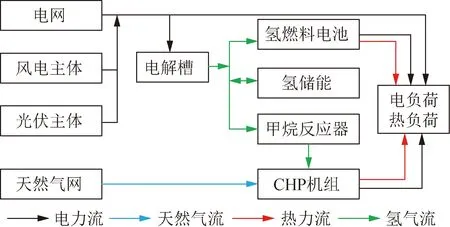
图2 CHP主体能量流动框架Fig.2 Energy flow frame of a CHP agent

CHP主体运行装置包括CHP机组、电解槽、甲烷反应器、氢燃料电池和氢储能设备，相应的模型描述如下：

1)CHP机组模型。

(11)

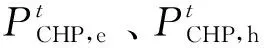
2)电解槽设备模型。

(12)

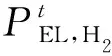
3)MR模型。

(13)

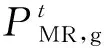
4)HFC设备模型。

(14)

5)氢储能设备模型。

(15)

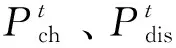
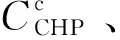
CHP主体的年化投资成本为：

(16)

式中：h表示CHP主体中设备之一；ΩCHP为CHP主体设备集，包括电解槽、MR、HFC和储氢罐；Yh为第h个设备的平均服务年限；Vh和θh分别为第h个设备投资容量和单位容量价格。

CHP主体向电网购电的成本和向天然气网购气的成本为：

(17)

综上，CHP主体的目标函数表示为：

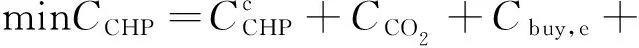
(18)

CHP主体合作运行的约束条件包括：电功率平衡约束、热功率平衡约束、天然气功率平衡约束、氢功率平衡约束以及各种运行设备约束(式(11)—(17))。

(19)

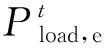
2 风-光-CHP多主体纳什谈判模型

本节首先建立风-光-CHP多主体纳什谈判模型，然后将其分解为系统运行成本最小化问题(P1)和交易支付问题(P2)；并在P2中提出考虑经济和环境增幅的议价能力模型，来保证合作收益的公平分配。

2.1 风-光-CHP多主体纳什谈判模型的建立

本文假设风电主体、光伏主体和CHP主体属于不同利益的主体，都具有个体理性和利益需求。各主体均希望通过合作来寻找一种最大提升各参与主体收益的运行策略[18]。纳什谈判理论属于合作博弈的范畴，可同时提升个体和整体的利益，使所有合作主体的效益最大化。因此，对风电主体、光伏主体和CHP主体应用纳什理论可得：

(20)

(21)

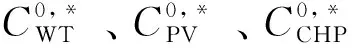
由于风-光-CHP纳什谈判模型为非线性模型，可将上述原问题分解成2个易于求解的子问题：风-光-CHP多主体能源系统运行成本最小化问题(P1)和交易支付问题(P2)。原问题的解可以通过依次求解P1和P2得到。

子问题1：系统运行成本最小化问题(P1)。

(22)

式中：mWT、mPV和mCHP分别为风电主体、光伏主体和CHP主体对于合作系统的运行成本参与度。

子问题2：交易支付问题(P2)。

(23)

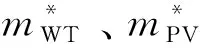
2.2 系统运行成本最小化问题(P1)求解

P1和P2均是混合整数规划问题，可通过集中式求解方法进行求解。传统集中式求解策略需要参与主体的大量隐私信息，不符合如今注重隐私信息的电力市场环境。而采用ADMM算法求解风-光-CHP多主体纳什谈判模型，各主体只需交互彼此的期望购电量和期望交易支付金额，不需要披露内部隐私[19]。因此为了保护各主体的运行隐私和减少通信负担，本文采用ADMM分布式求解算法对子问题P1和P2依次求解。

L1=(mWT+mPV+mCHP)+

(24)

通过采用ADMM算法分解技术，可将增广拉格朗日函数式(24)分解成风电主体、光伏主体和CHP主体分布式运行模型。

风电主体分布式运行模型为：

(25)

光伏主体分布式运行模型为：

(26)

CHP主体分布式运行模型为：

(27)

子问题P1基于ADMM分布式算法的求解步骤为：

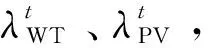
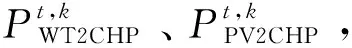
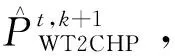
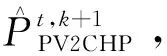
步骤5：更新拉格朗日乘子。

(28)

步骤6：更新迭代次数，k=k+1。

步骤7：判断算法收敛情况。若

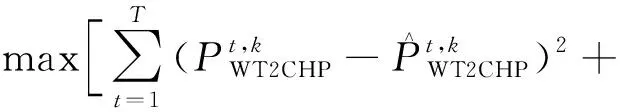
(29)

或k>kmax，迭代终止，否则返回步骤2重复计算。

2.3 基于议价能力的交易支付问题(P2)求解

在标准纳什谈判模型下，每个主体在交易支付中获得相同的利益分配数额，而风电主体、光伏主体和CHP主体在投资成本和效益评价指标等方面存在较大的差异，会导致合作无法继续进行。所以本文考虑从合作博弈带来的经济和环境增幅两方面来定义各主体的议价能力，即从购售能效益、投资成本、弃风量、弃光量和碳排放减少量等方面对风电、光伏和CHP主体在合作中的贡献程度和获益程度进行综合考虑。

1)效益增幅系数。

风电主体、光伏主体的效益增幅由售电收益和投资成本决定，CHP主体的效益增幅由购能成本和投资成本决定，则风电、光伏和CHP主体的效益增幅系数为合作前后的购售能效益与投资成本的比值。

(30)

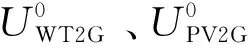
2)环境增幅系数。

环境增幅系数包括弃风改善系数、弃光改善系数和碳排放改善系数。

定义弃风改善系数LWT为风电主体合作前后弃风的减少量与投资成本的比值，代表风电主体通过合作提升的环境效益，表示为：

(31)

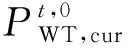
定义弃光改善系数LPV为光伏主体合作前后弃光的减少量与投资成本的比值，代表光伏主体通过合作提升的环境效益，表示为：

(32)

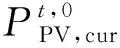
定义碳排放改善系数LCO2为CHP主体合作前后碳排放的减少量与投资成本的比值，代表CHP主体通过合作提升的环境效益，表示为：

(33)

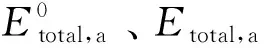
增幅系数可以表征风电主体、光伏主体和CHP主体通过合作获益的程度，增幅系数越大，代表该主体通过合作效益提升的程度越大。

为满足合作博弈中参与主体的个体理性，对于各参与主体获得的超额增幅应该按照增幅系数的反比进行分配，由此可以平衡主体之间的收益增量，促进合作的稳定。

定义经济议价因子α为：

(34)

定义环境议价因子β为：

(35)

由此可得，风电主体、光伏主体和CHP主体的议价能力η为：

(36)

在原交易支付问题(式22)的基础上，建立基于各主体议价能力的交易支付问题(P2)：

(37)

(38)

通过采用ADMM分解技术，可将增广拉格朗日函数式(38)分解成风电主体、光伏主体和CHP主体分布式交易支付模型，分别如式(39)—(41)所示。

风电主体分布式交易支付模型为：

(39)

光伏主体分布式交易支付模型为：

(40)

CHP主体分布式交易支付模型为：

(41)

子问题P2求解步骤和子问题P1求解步骤类似，故不做赘述。

3 仿真结果分析

3.1 ADMM算法收敛性分析

本文采用ADMM分布式算法对风-光-CHP多主体能源系统的系统运行成本最小化问题(P1)和交易支付问题(P2)进行求解。图3为P1的迭代收敛曲线，各主体运行成本函数曲线在迭代次数为41时，完成收敛，求解时间为81.16 s。图4为P2迭代收敛曲线，各分布式主体交易支付函数曲线在迭代次数为30时，完成收敛，求解时间为23.07 s。证明了采用ADMM分布式算法求解P1和P2，有良好的收敛特性，能在保护各主体隐私的前提下，高效求解。

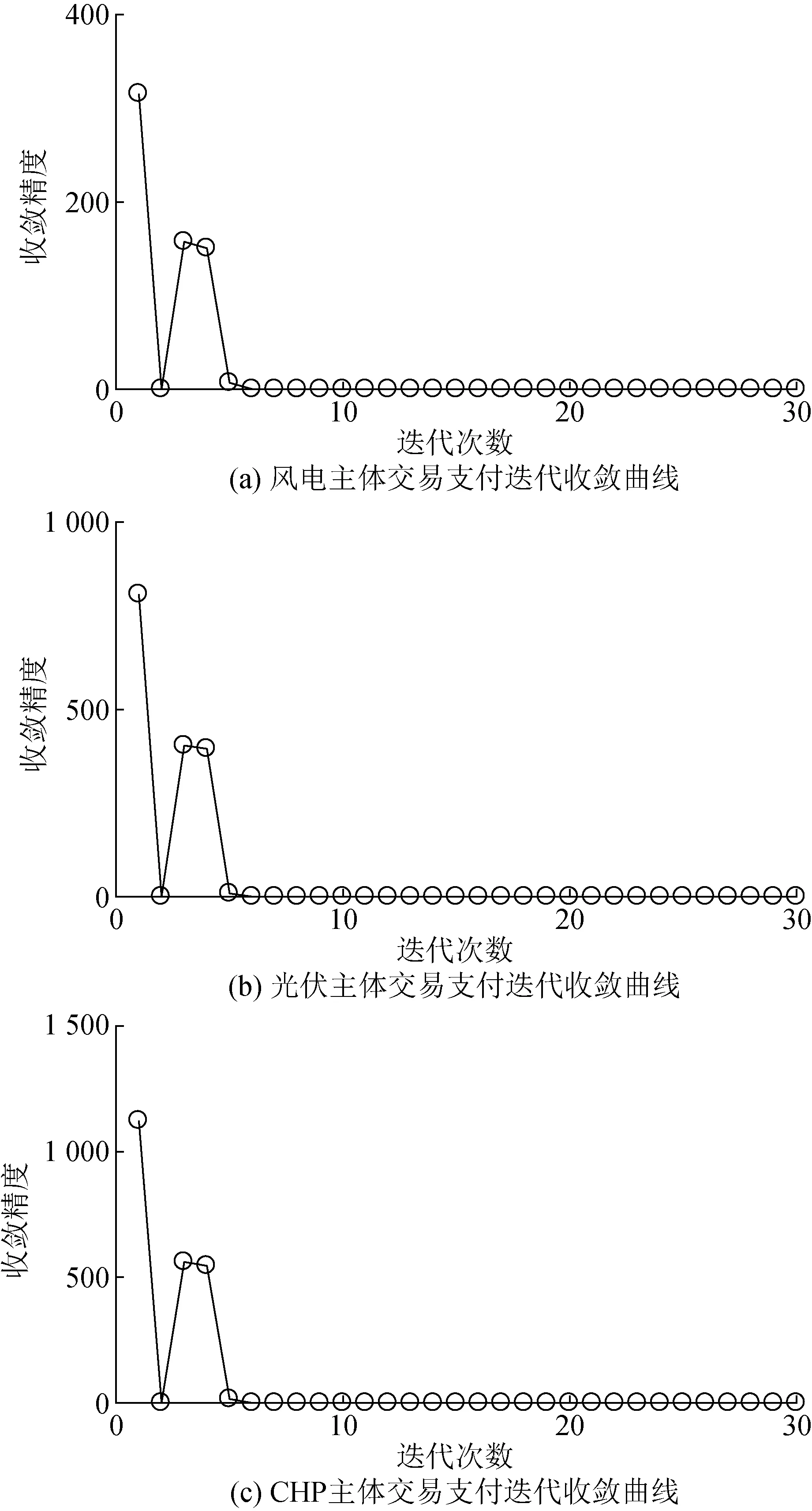
图4 P2分布式迭代收敛曲线Fig.4 The distributed iterative convergence curve of P2

3.2 风-光-CHP多主体能源系统环境增幅分析

表1为合作前后各主体的弃风、弃光和碳排放量。图5为CHP主体的电能交易结果。由表1和图5可以看出，风电主体和光伏主体在非合作运行策略下都会因上网功率限制，导致可再生能源不能完全消纳。在合作运行策略下，风电主体和光伏主体与CHP主体进行电能交易，实现了可再生能源的完全消纳。本文假设电网的电能均来源于发电厂燃煤机组发电，从电网购电会将燃煤机组的碳排放转移到购能方；从天然气网购气，购能方也会产生碳排放。消纳风电或光伏等可再生能源则不会产生碳排放。CHP主体在非合作运行策略下只从电网或气网购能，其碳排放量大幅增加。在合作运行策略下，可再生能源交易价格高于电网电价或气网气价时，CHP主体也会购买部分可再生能源用于电能供给，以维持其碳排放量在合适的区间，避免因阶梯型碳交易机制而造成碳排放成本大幅增加。所以在风-光-CHP多主体能源系统合作运行策略下，既实现了可再生能源的充分消纳，又大幅降低了CHP主体的碳排放量。

表1 合作前后各主体的环境增幅Table 1 Environmental gain before and after cooperation

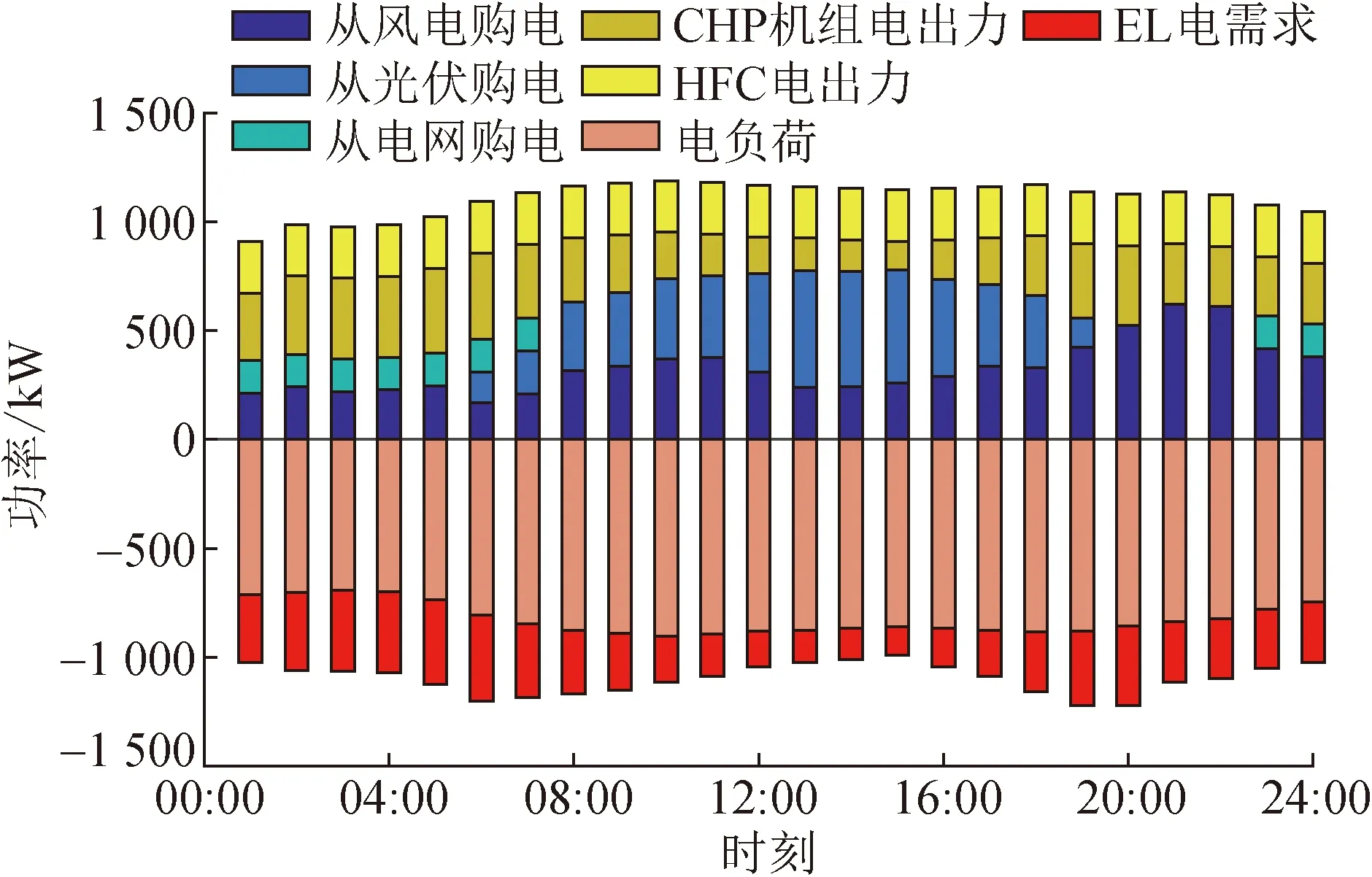
图5 CHP主体的电能交易结果Fig.5 Electricity trading results of the CHP agent

3.3 考虑议价能力的收益分配分析

基于议价能力的利益分配如表2所示，本文提出的考虑议价能力的风-光-CHP多主体优化运行策略相比非合作运行策略，风电主体、光伏主体和CHP主体的收益分别增加了1 934.9、1 398.3和4 173.5元，分别提升了52.97%、43.66%和20.10%，并且系统总收益提升了7 506.7元。证明了本文提出的考虑议价能力的风-光-CHP多主体优化运行策略的有效性，每个主体的收益都得到显著提升，可以兼顾个体和系统利益。

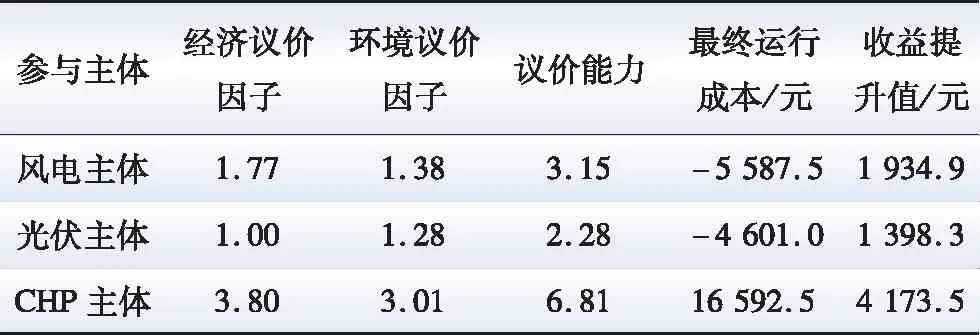
表2 基于议价能力的利益分配Table 2 Benefit distribution based on bargaining power

表3为标准纳什谈判模型合作前后成本与收益。当基于标准纳什谈判方法进行收益分配时，每个主体的效益提升额基本相等，约为2 502.2元。然而，各个主体在装机容量规模、成本结构和效益评价等方面存在较大的差异，平等地分配利益显然是不公平的，不利于合作的继续进行。采用本文提出的基于经济和环境增幅的议价能力模型时，议价能力较大的主体会获得更多的利益分配。由表2可知，CHP主体的议价能力为6.81，因此获得较多的利益分配额度；而风电和光伏主体的议价能力分别为3.15和2.28，获得较少的利益分配额度。证明了考虑议价能力的交易支付模型能够使参与主体获得公平的利益分配，促进合作的进行。

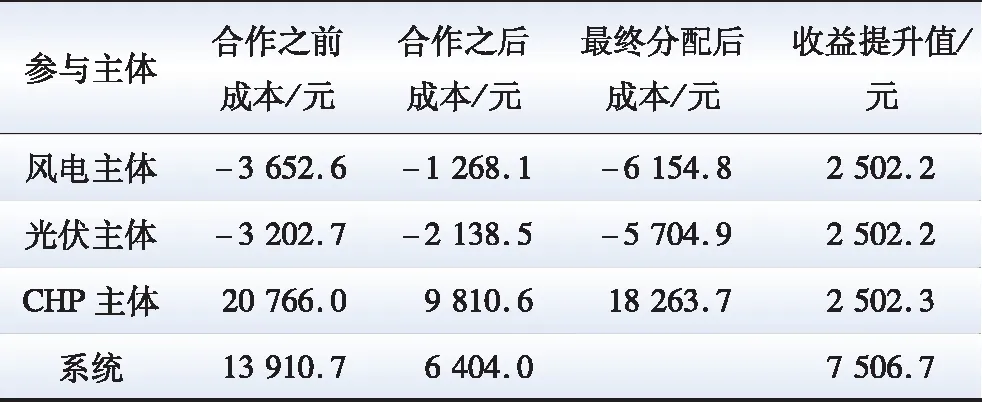
表3 标准纳什谈判模型合作前后成本与收益分析Table 3 Cost and benefit analysis of standard Nash negotiation model before and after cooperation

3.4 电制氢技术效益分析

电制天然气的效率仅为55%，而电制氢气的效率高达80%，并且氢气具备燃烧效率高和不产生碳排放特点[20]。为了体现将电制氢技术替换电转气技术的策略优势，分析了3种CHP主体的运行情景。

情景1：CHP主体中引入电制氢技术。

情景2：CHP主体为电转天然气技术。

情景3：CHP主体不含有电制氢和电转气技术。

3种运行情景下的调度结果如表4所示。

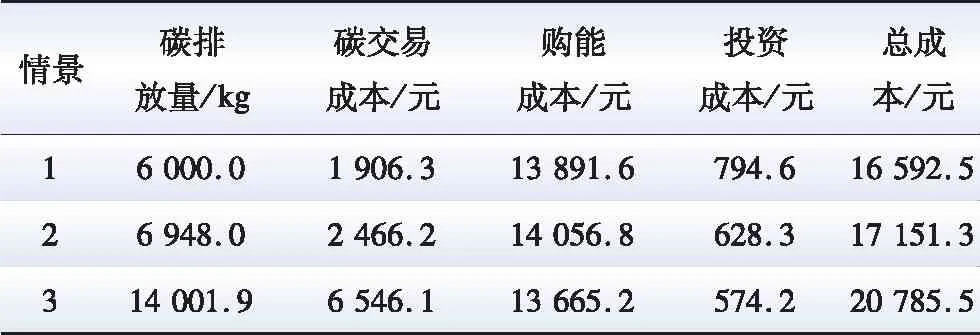
表4 不同场景下CHP主体的效益对比Table 4 Benefit comparison of CHP agent in different scenarios

由表4可知，情景1的运行总成本最低，相比情景2、情景3分别降低了558.8、4 193.0元。碳排放量方面，情景1相比情景2减少了948.0 kg，相比情景3减少了8 001.9 kg。由于情景3不含能量转换装置，CHP主体必须购能来满足自身负荷需求，因此其运行成本和碳排放量最多。情景2和情景3都含有能量转换装置，情景2中电转气技术包含电制氢和氢气甲烷化2个环节，电制氢环节的产氢全部经MR合成天然气，天然气再输送到CHP机组进行热电联产。情景3中电制氢的氢能直接到HFC进行热电生产，不会造成多个梯级的能量损耗，并且HFC中氢能相比CHP机组中天然气的能效更高。所以情景3的运行成本和碳排放量最低，验证了运用电制氢技术的策略优势。

4 结 论

在电力系统重视低碳经济运行的背景下，本文将综合能源系统细分为风电主体、光伏主体和CHP主体，深入分析了其运行特性，并在CHP主体中增加电制氢技术和阶梯型碳交易机制。然后构建了基于纳什谈判理论风-光-CHP多主体合作运行模型，将其分解为系统运行成本最小化问题(P1)和交易支付问题(P2)，并在P2中提出了基于议价能力的收益分配策略。最后，采用交替方向乘子法，对P1和P2进行分布式求解。主要得出以下结论：

1)本文所提考虑议价能力的风-光-CHP多主体优化运行策略，能够公平分配多主体合作后的收益，满足各参与主体的个体理性。议价能力越大的主体，分配的收益越大，有效激励各主体参与合作的积极性。

2)CHP主体中引入电制氢技术和阶梯型碳交易机制，约束盈余可再生能源或电价谷段电网电能充分参与到电制氢环节，发挥氢能燃烧效率高和不产生碳排放的特点，进一步促进CHP主体低碳经济运行。

3)本文采用交替方向乘子法分别求解系统运行成本最小化和交易支付2个子问题。该方法仅需要交换有限的内部信息，因而能够有效保护各参与主体的隐私，且具有良好收敛性。