面向互联电网连锁故障安全防控的关键支路辨识

段忠峰，王亚松，白茂金，刘威，朱春萍，王成福，董晓明

(1.山东电力工程咨询院有限公司，济南市 250013；2. 电网智能化调度与控制教育部重点实验室(山东大学)，济南市 250061)

0 引 言

随着国内电网规模的日益增大，电网互联[1-2]可以有效地提高供电的可靠性，使调配用电更加合理，同时提高电厂的经济性。然而，国内外相继发生的多起大停电事故表明，互联电网关键支路的失效在大停电事故连锁故障的发展过程中起到了重要的助推作用，严重威胁了电网的安全稳定运行[3-6]。因此，准确辨识出对系统安全运行至关重要的关键支路，对于提高系统的供电可靠性具有重要意义[7]。

目前，针对互联电网关键支路辨识的理论研究主要包含复杂网络理论和自组织临界理论[8-10]。复杂网络理论首先将电力系统抽象为一个连通图，然后基于图论和复杂网络理论对该连通图进行分析，辨识出系统的关键支路[11-13]。研究表明，具有较高介数[14]或混合介数[15]指标的支路通常为系统的关键支路。基于复杂网络理论的关键支路辨识方法具有一定的准确性和计算效率，但该方法简化了系统的潮流特性、刚性约束及调整能力，削弱了电力系统的功能特性，更多的是从网架结构角度分析支路的重要程度，具有一定的局限性。基于自组织临界理论的电网关键支路辨识方法，通常基于各种潮流理论，考虑系统潮流转移、电网调整和安全自动装置等多种因素，构建支路失效后连锁故障的演化模型[16-17]，然后通过大规模连锁故障的仿真模拟，进行关键支路的有效辨识。在基于直流潮流连锁故障模型[18-19](ORNL-PSERC-Alaska，OPA)的基础上，文献[20]提出了一种考虑系统输电网架升级和源荷增长的连锁故障仿真模型，能够有效分析电网一次设备失效后的系统状态。文献[21]使用风险价值、条件风险价值和负荷损失期望值等多种风险评估指标对OPA仿真模型的结果进行量化，实现了系统关键支路的辨识。文献[22]基于交流潮流理论，提出了改进的Manchester连锁故障仿真模型，并通过模拟系统的低压减载和低频减载保证了交流潮流的收敛性，然后依据支路开断下的系统停电风险量化支路的重要程度。针对连锁故障中交流潮流不收敛的问题，文献[23]引入连续潮流，通过节点电压和负荷的灵敏度进行负荷切除以保证系统稳定和潮流收敛。在交直流混联的电网背景下，文献[24-26]开展了交直流混联系统的连锁故障仿真，其核心是在潮流结果的基础上，增加交直流系统相互作用的环节，即通过直流母线换流站的电压情况判断直流输电线路的运行状态。基于交流潮流或交直流潮流的电力系统连锁故障仿真模型，虽然能够更为全面地反映系统运行状态的变化，但针对潮流不收敛问题的处理过于主观，且计算复杂、效率低下。

相比于复杂网络理论，基于自组织临界理论的电网关键支路辨识方法能够较好地计及系统的潮流特性，给出支路失效后连锁故障的发展过程及其对系统的影响，更加准确地识别电网的关键支路；但现有的基于自组织临界理论的关键支路辨识方法普遍存在两个问题：1)基于直流潮流和交流潮流理论的连锁故障模型在计算精度和潮流收敛性上存在矛盾；2)连锁故障中常忽略系统自动控制装置的作用及系统的校正控制措施，无法准确评估连锁故障对系统造成的影响，继而导致关键支路的筛选存在偏差。

为此，本文提出基于过载型连锁故障的电网关键支路辨识方法。首先，推导计及无功电压的改进直流潮流算法，该算法实现对系统无功和电压的快速估算且不存在潮流发散问题；其次，建立过载型连锁故障仿真模型，该模型考虑系统功率平衡和电压稳定装置的调节作用以及系统的校正控制措施，能够较好地模拟支路失效后系统连锁故障的动态演化过程，并计算出连锁故障对系统造成的功能和结构损失；然后，给出电网支路重要度评估指标，借助于连锁故障动态演化模型对系统进行大量故障模拟并计算出各支路重要度指标，从而实现关键支路的筛选。最后，基于IEEE 39节点系统的算例分析，验证所提模型和方法的有效性。

1 计及电压和无功的直流潮流算法

计及电压和无功的改进直流潮流算法，首先基于传统的直流潮流获得系统各节点的电压相角，然后利用节点注入功率方程推得节点电压幅值的线性化表达式，进而得到节点电压的估算值，最后根据电压相角和幅值进行系统无功功率分布的估算。具体的计算过程如下。

电力系统的连锁故障通常发生在高压环网中，网络较小的阻抗比保证了直流潮流的计算精度，传统的直流潮流方程表示如下：

P=Bθ

(1)

式中：P为节点有功注入功率构成的列向量；B为忽略支路电阻的节点导纳矩阵；θ为系统节点电压相角列向量，由此可以求得系统各节点的电压相角值。

对于PQ节点i，其复功率可以表示为：

(2)

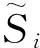
(3)

(4)

式中：ΩPQ和Ωelse和分别代表PQ节点和非PQ节点构成的节点集合；θi和θk分别为节点i、k的电压相角。对式(4)进一步变换可得：

(5)

设：

(6)

则式(5)可以表示为：

(7)

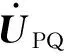
对于正常运行的网络，假设PQ节点的电压幅值均为1 pu，则有：

(8)

将式(8)代入式(7)中，可得到UPQ的近似解为：

(9)

式中：等号右侧均为已知量，因此该算法仅需一次计算就可得到PQ节点的电压幅值，然后在已知节点电压相角和幅值的条件下可对系统的无功分布进行估算。

2 过载型连锁故障演化模型

2.1 连锁故障动态演化过程

电网中载流支路发生故障时，一方面会破坏系统原有的拓扑结构，甚至造成电网解列；另一方面会破坏系统的功率平衡，造成潮流的大规模转移。在电网高度互联的情况下，大规模的潮流转移极易引发相邻设备的载流越限，导致其在继电保护装置作用下退出运行，进而引发新的故障。电网在级联故障下，系统功能和结构受到较大破坏，最终导致大停电事故。此外，在潮流转移期间，系统的自动安全装置会及时调整，维持系统的功率平衡和电压稳定，且载流设备通常允许一定时间的持续过载，这为紧急运行状态下系统的校正控制提供了契机，可以通过快速地调整控制措施快速消除过载，避免后续支路的开断和连锁故障的发生。由此可以发现，电力系统的连锁故障是一个连续的复杂的动态过程。基于上述描述，给出电力系统连锁故障动态演化过程模拟流程，如图1所示。

图1 过载型连锁故障动态演化过程流程Fig.1 Flow chart of dynamic evolution process of overload cascading fault

具体的计算过程如下所述：

1)针对正常运行的系统网络，设定载流支路因故障停运，模拟系统的源发型故障。

2)对网络进行拓扑分析，更新各子网的电源、网架结构和负荷等信息。

3)逐一计算各区域子网。对于既有负荷也有电源的子网转4)，对于不同时包含负荷和电源的子网转6)。

4)针对既有负荷也有电源的子网做如下计算：

(1)根据2.2节中的功率平衡调节策略，模拟系统功率平衡装置，调节系统功率。需要注意的是，对于节点型子网(仅包含一个节点母线的网络)，功率平衡调节后，不需要进行潮流计算和校正控制，转6)；对于区域型子网(包含多个节点母线的网络)转(2)。

(2)根据第1节对该子网进行改进直流潮流计算，求得系统节点电压幅值和支路功率。

(3)判断节点电压是否过低，对于电压较低的节点，模拟系统电压稳定装置，对低电压节点进行一定比例的负荷减载，然后转(1)，否则转(4)。

(4)判断支路是否超过稳定极限，针对所有超过其稳定极限的输电支路，模拟系统继电保护装置的动作，切除过载支路，然后转2)；若无过载支路则转5)。

5)对于没有发生连锁故障的子网区域，采用2.3节给出的校正控制策略进行调整，保证系统的安全稳定运行。

6)存储子网电源、网架结构和负荷等信息。

7)判断所有子网是否计算完成，如没有则转3)，否则转8)。

8)输出该系统连锁故障后各子网的电源、网架结构和负荷信息以及连锁故障事故链，事故链即为连锁故障过程中失效支路构成的链条。

2.2 故障过程中的功率平衡策略

故障会破坏系统原有的功率平衡，而区域子网的功率平衡是潮流计算的前提，因此在潮流计算前应首先进行区域子网的功率平衡调节。故障过程中的功率平衡策略如图2所示。

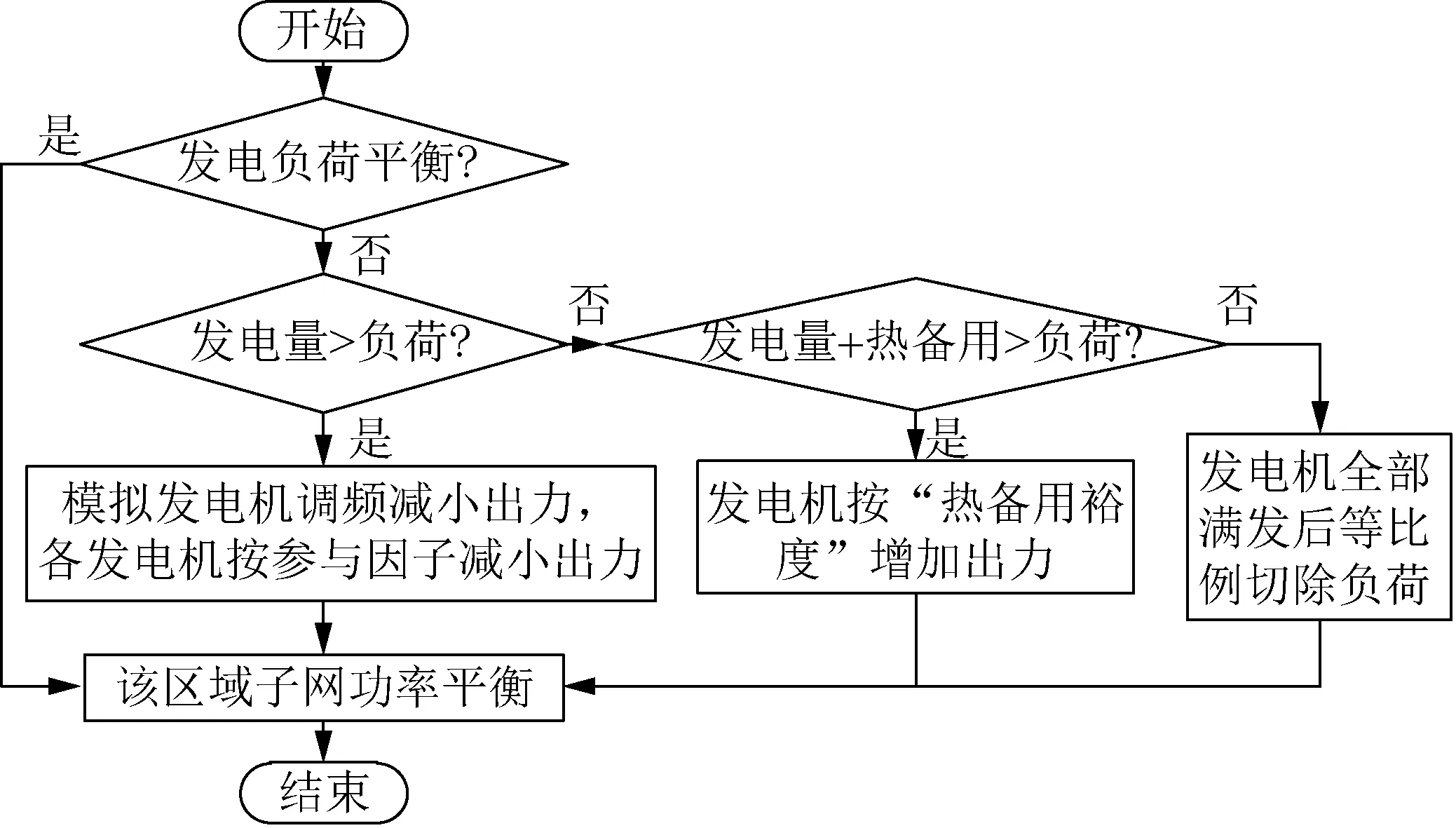
图2 故障过程中的功率平衡策略Fig.2 Power balance strategy in fault process

具体调整策略如下：当区域子网发电量大于负荷时，各发电机按照其参与因子大小减小出力，维持系统的功率平衡；当发电量小于负荷但当前发电量与机组热备用之和大于负荷时，发电机组按照“热备用裕度”增加出力，该调节策略可以保证在调节过程中，不出现发电机组出力超越上限的情况；若当前发电量与机组热备用之和仍小于负荷，首先设定发电机投入所有的热备用，尽可能满足负荷需求，然后再等比例切除负荷，维持系统的功率平衡。

2.3 故障过程中的校正控制策略

载流支路通常允许一定时间的持续过载，对于存在过载支路且其载流量未达到稳定极限的系统，可以通过校正控制使其回到安全运行状态。本文将停电损失与电网校正控制的优化问题相结合，提出在系统安全约束范围内，寻求停电损失最小的校正控制模型，其目标函数为：

(10)

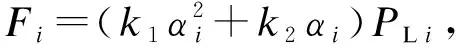
校正控制模型的等式约束为：

(11)

式中：ΔPi、ΔQi分别为节点i的有功功率和无功功率的功率误差；PGi和QGi为节点i上发电机的有功和无功输出功率；QLi为节点i上负荷的无功功率，节点上的负荷采用恒定功率模型，且在切除过程中保持负荷功率因数不变；Pij、Qij分别为线路ij上传输的有功功率和无功功率。

校正控制模型的不等式约束包括：

1)发电机有功无功出力上下限约束：

(12)

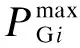
2)节点负荷切除比例上下限约束：

(13)

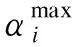
3)节点电压上下限约束：

(14)

4)支路载流约束：

(15)

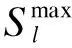
5)有载变压器分接头位置约束：

(16)

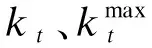
(17)

式中：Gii(Gjj)和Bii(Bjj)分别为自电导和自电纳；Gij和Bij分别为互电导和互电纳；YT为变压器支路的串联导纳。

6)并联电容器接入比例约束:

(18)

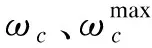
Gii+jBii=0+jωcBc

(19)

式中：Bc表示并联电容器的电纳。

校正模型本质上为一种最优潮流模型，即在各变量约束条件构成的可行域内，考虑各种控制装置的调节作用，求得系统停电损失最小的运行状态，该模型可借用非线性规划求解器进行求解。

3 载流支路重要度评估指标

为更好地评估载流支路失效引发的连锁故障对系统造成的影响，定义负荷损失率和支路损失率2个指标分别从系统功能和结构两个方面量化连锁故障对系统造成的损失，所定义的指标可直接根据连锁故障演化模型的输出结果进行计算。

负荷损失率为连锁故障后负荷有功功率切除量占系统原有功功率总量的比值。

(20)

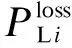
支路损失率为连锁故障发展过程中失效的支路数占系统原支路总数的比值。

(21)

电网的载流支路，既可以作为源发型故障诱发连锁故障，也可以以级联失效的形式出现在连锁故障的发展过程中。因此，可以通过对系统进行大规模的连锁故障仿真，得到各连锁故障对应的事故链、负荷损失率和支路损失率，根据各支路在事故链中出现的概率及对系统造成的损失，计算各支路的重要度指标，从而筛选出关键的支路。

表征支路l对系统功能重要性的指标定义如下：

(22)

式中：m1为大规模连锁故障仿真得到的事故链集合；m2为包含支路l的事故链集合；nm1和nm2分别为集合m1和m2对应的事故链数目；RPL∈m2即为集合m2中事故链对应的负荷损失率。

表征支路l对系统结构重要性的指标定义如下：

(23)

式中：RLL∈m2即为集合m2中事故链对应的支路损失率。

4 算例分析

为验证本文所提模型与算法的有效性，选取标准IEEE 39节点系统进行计算分析，其网架结构如图3所示，其中节点8、14、18上均安装有大小为0.05 pu并联电容器，系统其他参数取自MATPOWER7.0。

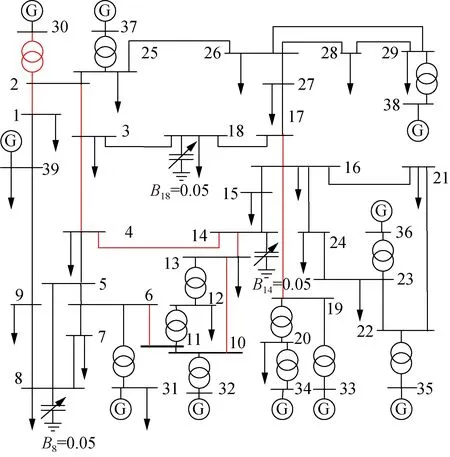
图3 IEEE 39节点系统结构图Fig.3 IEEE 39-bus system structure diagram

4.1 改进直流潮流算法有效性分析

为验证改进直流潮流算法的收敛特性及计算性能，在不同的负荷水平(1.2、1.4、1.6、1.9、2.0、2.2 pu)下对IEEE 39节点系统进行计算，并以牛顿-拉夫逊潮流方法的计算结果作为对比进行分析。不同负荷水平下两种方法PQ节点电压幅值计算结果如图4所示，以牛顿-拉夫逊法所得结果作为参考值求得的电压幅值最大误差百分比及两种方法的计算时间如表1所示。

图4 PQ节点电压幅值计算结果Fig.4 Result of voltage amplitudes at PQ buses

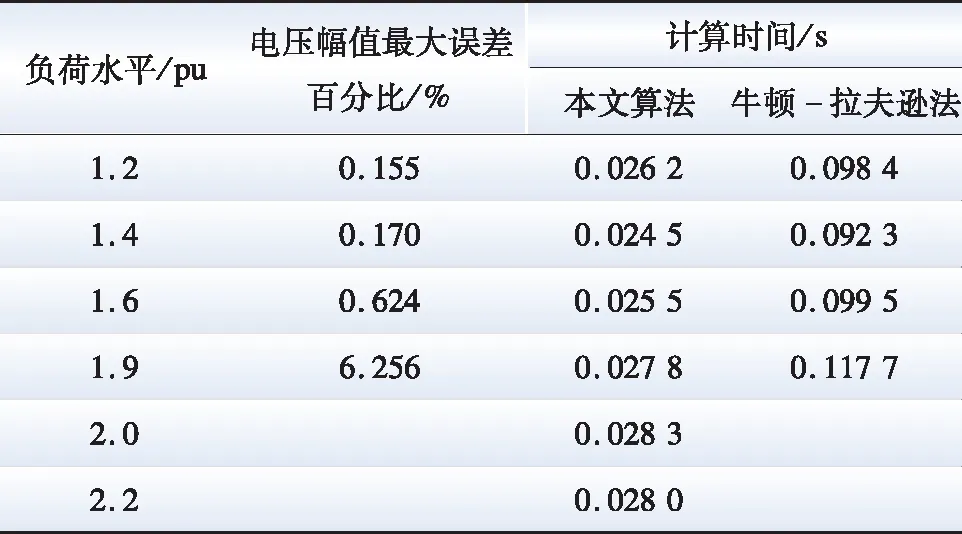
表1 电压幅值计算误差及算法计算时间比较Table 1 Comparison of voltage amplitude calculation error and algorithm calculation time

在轻负荷(负荷水平为1.2、1.4、1.6 pu)的情况下，随着负荷水平的逐渐增加，本文所提算法与牛顿-拉夫逊算法的电压幅值计算结果的误差逐渐增大，但电压幅值最大误差百分比均在1%以内；当系统的负荷水平增大至1.9 pu时(系统收敛临界负荷水平为1.92 pu)，电压幅值最大误差百分比为6.256%，算法仍旧保持着较好的计算精度，且在以上4种情况下，本文所提算法的平均计算时间仅为牛顿-拉夫逊算法的1/4。在过度重载(负荷水平为2.0、2.2 pu)的情况下，牛顿-拉夫逊算法不收敛，无法求得系统状态，而本文所提算法依旧收敛，可以进行电压的估算，将其与低压减载方案相配合，能够快速求得系统减载后的状态信息。

综上所述，计及电压和无功的改进直流潮流算法能够在保证潮流收敛的情况下，实现对系统电压和无功的快速估算，且计算精度可满足系统大规模连锁故障仿真的计算需求。

4.2 系统关键支路辨识分析

正常运行情况下，系统应满足N-1安全准则，单一支路故障对系统的影响较小，且系统发生多重支路故障的概率也较低，因此本算例在N-2源发型支路故障下对系统进行连锁故障模拟。

取各发电机的热备用为其最大有功功率的10%，参与因子为其最大发电量占系统总发电量的比例；支路稳定极限传输容量设置为其最大传输容量的1.2倍；设置低压减载阈值为0.92 pu，针对低于该阈值的负荷节点，按照当前节点负荷比例的20%进行逐次减载。在额定负载水平下对系统进行仿真分析，共计得到1 035条事故链，按照所定义的载流支路重要度评估指标，分别计算出表征支路对于系统功能重要性和结构重要性的指标Fbra、Tbra，并按照Fbra进行降序排列，相关结果见表2。

支路的Fbra和Tbra指标越大，代表该支路出现在连锁故障事故链集合中的频率越高，且对系统的功能和结构造成的破坏越大，继而表明该支路的重要度越高，图3中标出了Fbra指标排名前10的输电支路，由系统结构图可以发现，这些支路主要是系统各区域之间的重要联络线，此类线路的故障将造成区域功率失衡及潮流的大规模转移，继而引发更大规模的级联故障，这也进一步佐证了基于过载型连锁故障进行关键支路辨识的有效性。

为验证指标Fbra和Tbra的相关性，图5给出了支路Fbra和Tbra指标数据图，图中横轴支路序号与表2中的支路序号相同。由图5可知：1)从整体上看支路的Fbra和Tbra指标之间具有较强的相关性，Fbra和Tbra的变化趋势相同，这表明关键支路的故障对系统功能和结构的影响是共存的，系统结构大规模的破坏，将严重削弱系统的功能；2)针对具体的某一支路，Fbra和Tbra表征的线路重要度可能存在较大差异，例如支路6(L6-11)，其Tbra指标在所有输电支路中的位次为第2位，但其Fbra指标位次为第6位，这表明L6-11所属的连锁故障对系统结构的影响较大，但在系统校正控制的作用下，并没有对系统功能造成很大的影响。

表2 载流支路重要度评估结果Table 2 Evaluation results of the current-carrying branches

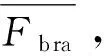
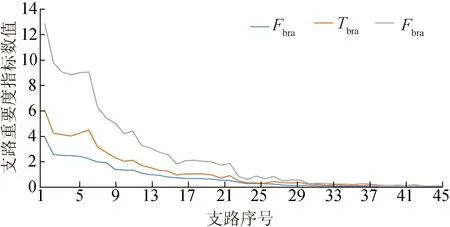
图5 支路Fbra和Tbra指标数据图Fig.5 Index data of Fbra and Tbra

5 结 论

本文针对潜在引发电网连锁故障的关键支路辨识问题，提出了一种基于过载型连锁故障的电网关键支路辨识方法。基于改进直流潮流构建的过载型连锁故障仿真模型考虑了系统功率平衡和电压稳定装置的调整过程以及系统的校正控制策略，能够较为准确地模拟载流元件失效后系统连锁故障的动态演化过程并计算出该连锁故障对系统造成的功能和结构影响。给出了系统支路重要性评估指标，通过对系统进行大规模连锁仿真，实现了电网关键支路的有效辨识。基于IEEE 39节点的案例分析表明，所提模型和算法能够有效识别出能够引发系统连锁故障的关键支路，并证明了紧急情况下系统的校正控制措施能够大幅度提高系统的运行维持能力，能够有效缩小事故范围，减小负荷损失。