基于GIM模型的输电线路通道隐患快速检测

齐立忠 ,张苏, 张亚平, 孙小虎

(国网经济技术研究院有限公司，北京市 102209)

0 引 言

在架空输电线路工程设计阶段，快速、准确地获取设计导线与通道中植被、建筑、道路以及交跨线路等各类地物之间的空间距离，实现输电线路通道隐患快速检测对于设计方案寻优、工程造价计算以及通道清障工作具有重要意义。在传统设计中，通道隐患排查仅考虑通道地物在导线风偏面内的平面距离是否满足对应的安全距离要求，然而当导线弧垂变化较大时导线距离地物点的最近点往往不在风偏面上，导致最近距离计算变大，存在漏检风险。随着电力工程设计模式从传统二维向三维转变，为进一步实现快速、准确的架空输电线路工程设计阶段通道隐患检测提供了数据基础。

为了解决不同软件之间的电网三维设计数据交换问题，国家电网有限公司制定了统一电力工程三维设计数据标准，即电网信息模型(grid information model，GIM)，GIM技术成为了电力工程三维设计未来发展的主流方向。目前，已有大量学者开展了基于GIM模型的相关应用研究[1-8]，但关于输电线路通道隐患检测方面的相关成果较少。在现有文献中，由于无法直接求解三维点到GIM电力线曲线的最近距离，在部分研究中采用了近似方法进行求解。文献[9]在地物点到电力线空间曲线最近距离求解问题上提出一种近似计算方法，将xOy平面上电力线空间曲线投影到地物点平面距离最小点视为电力线空间曲线到地物点的最近点，该方法与传统二维设计隐患检测原理一致，未发挥出三维设计的空间特性优势，存在隐患点漏检情况。与此同时，有学者从另一思路出发，将导线点集化后通过计算点到离散点集最近距离实现隐患检测。文献[10]在基于GIM的架空输电线路建模中，基于悬链线方程对电力线模型进行离散点集化，实现了三维点到电力线的最近距离计算，然而悬链线方程无法直接求解指定线长下的电力线位置，该方法采用传统等水平间隔的采样方法，采样点分布并不均匀，影响高山区、重大交跨等特殊档隐患检测精度。在优化通道隐患检测效率方面，文献[11]提出一种基于网格化的优化算法，对地物点进行规则网格化，认为当网格内最高点满足安全距离要求时，该网格内不存在隐患点，跳过该网格内其他地物点的隐患判断计算，以到达加快检测效率的目的。但对于高大树木、建筑而言，导线可能位于侧方而非上方，此时该方法易导致隐患点漏检。

为解决现有输电线路GIM通道隐患检测方法存在漏检多检、检测效率低下的问题，提出一种基于等线长点集化和球体包含原理的通道隐患快速检测方法。在本文算法中，首先，采用等线长间隔采样方式将导线由空间曲线转化为离散点集，使离散点集在电力线上均匀分布，解决传统等水平间隔采样方式离散点集分布不均匀、特殊档精度较差的问题；其次，在地物点到电力线离散点最近距离计算过程中引入球体包含原理对地物点隐患可能进行严密判断，对不存在隐患可能的地物点跳过邻近点搜索计算，实现通道隐患快速检测。应用表明，该方法在保证计算精度的前提下达到隐患点检测效率优化的目的，将隐患检测耗时优化为传统逐点检测耗时的6.9%，对GIM的进一步应用推广具有重要作用。

1 基于GIM模型的输电线路通道隐患快速检测算法

1.1 输电GIM文件信息结构

GIM文件本质上是一种分层次的电力设施属性文件，在输电工程中分为5个层次级别，分别为全线级、分段级、耐张段级、设备组级以及设备级，具体信息如图1所示。

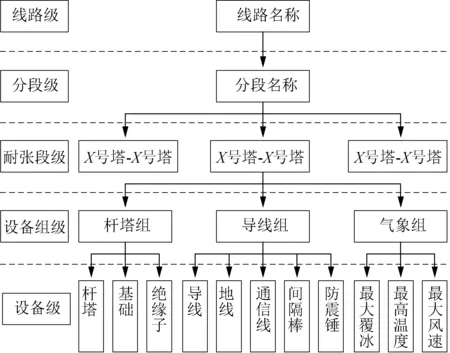
图1 输电GIM文件信息结构Fig.1 Transmission GIM file information structure

图1中设备组一级定义了各耐张段内杆塔、基础、导地线以及对应控制工况信息，其中杆塔部分记录各杆塔模型节点坐标与挂点坐标；气象部分记录各个设计工况的气象条件；导线部分对应属性信息，如表1所示。

表1中，各项电力线参数与温度、覆冰、风速等气象因素结合即可计算出自重比值、冰重比载以及风偏比载，其中自重比值、冰重比载之和为垂直比载，风偏荷载为水平比载。

表1 导线属性信息表Table 1 Wire attribute information table

1.2 电力线空间位置曲线离散点集化

由于无法直接在三维空间内求解三维点到空间曲线的最小距离，在通道隐患检测中往往采用近似方法进行求解，易发生隐患点多检漏检情况。相反，三维点到离散点集的最小距离求解相对简单，因此本文基于导线点集化思想，将导线空间曲线转化为具有一定间隔的离散点集，通过点到点集最小距离计算实现通道隐患检测。

1.2.1任意气象条件下的导线三维位置计算

在目前的电力线力学研究中，通常认为自然条件下电力线形态符合悬链线分布，其在挂点连线竖直平面投影分布如图2所示。

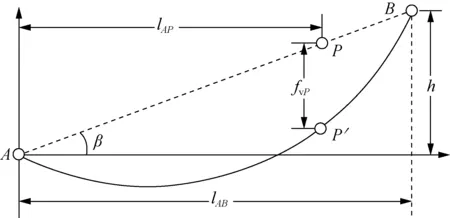
图2 挂点连线竖直平面内电力线形态分布示意图Fig.2 Schematic diagram of vertical plane power line distribution form of hanging point connection

图2中：A点与B点分别为电力线两侧挂点，lAB为挂点A与挂点B在水平面上的投影距离，h为挂点A与挂点B高程差值，点P为挂点AB连线任意一点，P′为点P在电力线上对应点，lAP为挂点A与点P在水平面上的投影距离，fvP为点P对应的弧垂值，β为高差角，由挂点A、B之间高差值h与水平距离lAB计算确定。

(1)

式中：fhP为点P对应的风偏值；γv、γh分别为指定气象条件下导线的垂直荷载与水平荷载；σ0为指定气象条件下导线最低点的应力值。γv、γh与σ0由导线设计参数结合指定的气象参数通过状态方程计算确定，具体理论与步骤参照文献[11-17]。根据任意点P三维坐标，结合弧垂值fvP、风偏值fhP以及AB连线可推算出点P对应导线点的三维坐标。

1.2.2基于等线长间隔的电力线离散点集化

在现有研究中，通常通过调整挂点A与电力线上任意点P在水平面上的投影距离lAB，每隔一定水平间距dl求解一次lAP对应的弧垂与风偏值，进而得到导线空间曲线的离散点集，离散点集分布如图3所示。

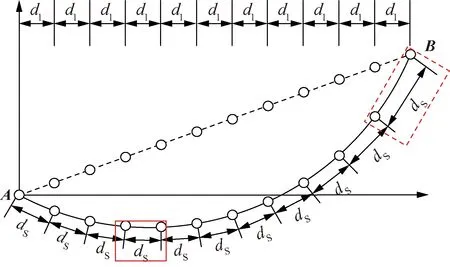
图3 等水平间隔采用下电力线离散点集分布图Fig.3 Distribution diagram of power line discrete point set with equal horizontal interval

水平间隔dl的选取直接影响通道隐患检测的检测效果，水平间距选取过大，电力线点集过于稀疏，易导致隐患检测漏检；水平间距选取过小，导线点集过于密集，影响最小距离计算效率，在现有研究中水平间距dl一般选取0.10 m。

从图3中可以看出，采用等水平间距采样方式，存在离散点集在电力线上分布并不均匀的问题。图3中虚线框中线长间隔dS较实线框中线长间隔明显较长，且随着挂点A与挂点B档距lAB、高程差值h以及线路设计最大弧垂的增大，虚线框中线长间隔dS将进一步增长，较大可能达到水平间距dl的1.5～2.0倍。此时，虚线框附近的地物点到电力线最近点的定位极限误差控制在0.10 m左右，不符合精度控制要求，易导致隐患点漏检。因此，本文采用等线长间隔的采样方法，如图4所示使得离散点集在电力线上呈均匀分布，采用0.10 m的间隔时，将地物点到电力线最近点的定位极限误差控制在0.05 m以内，以保证隐患检测精度。

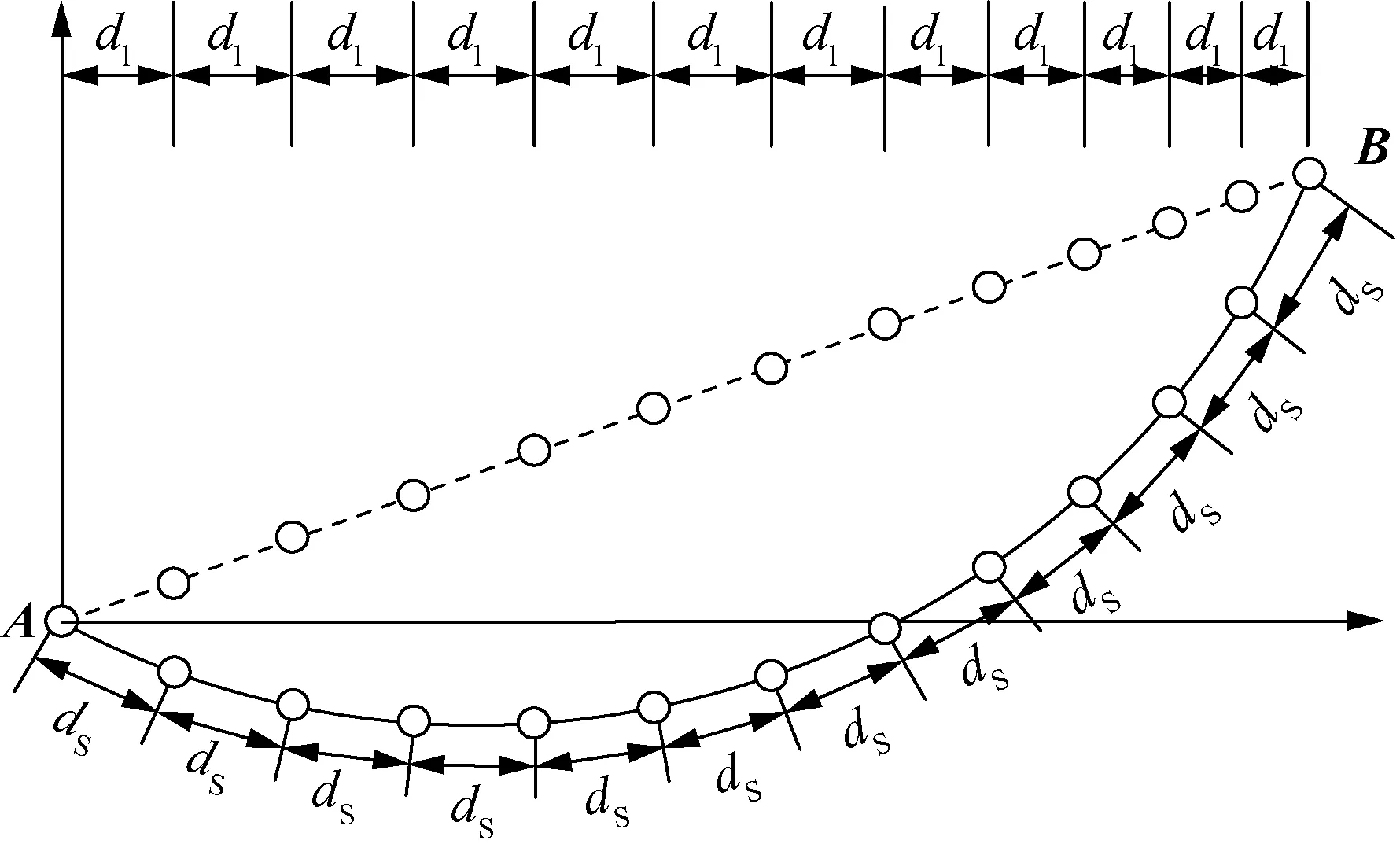
图4 等线长间隔采用下电力线离散点集分布图Fig.4 Distribution diagram of discrete point set of lower power line with equal line length interval

由于电力线在较小的局部区域可视为沿空间直线分布，基于此本文利用待计算点之前的两个采样点构造空间直线方程，并将该空间直线视为待计算点与其前一采样点之间的电力线分布，通过计算空间直线在挂点水平连线上的单位投影长度实现线长间隔到水平间隔之间转换，具体步骤如下：

步骤1：由导线设计参数结合指定的气象参数通过状态方程计算得到γv、γh与σ0三个参数值；

步骤3：计算挂点A处的初始区域空间直线向量，取lAB=0.2dS代入式(1)计算临时点Pt的风偏值与弧垂值，从而推算点Pt坐标为(Xt,Yt,Zt)；

步骤4：令PS=Pt，PE=A，lAP=0，i=1；

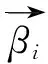
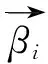
(2)

步骤7：计算采样点坐标，令lAP=lAP+dl代入式(1)计算采样点的风偏值与弧垂值，得到采样点Pi坐标为(Xi,Yi,Zi)并加入到电力线离散集中；

步骤8：令PS=PE，PE=Pi，i=i+1，重复步骤5—8，直至lAP>lAB，算法结束，得到电力线离散点集。

1.3 基于球体包含原理的通道隐患快速检测

目前，点到点集最近距离的计算问题基本是通过邻近搜索算法解决的，然而在输电线路通道隐患检测中，一个塔段通道的相关地物点数量级在千万以上，在隐患检测中需计算每个地物点到电力线点集的最近距离，单个塔段就需要进行上千万次邻近搜索运算，效率低下、无法满足隐患检测效率需求[18-20]。

文献[10]在优化通道隐患检测效率方面提出一种网格法的优化算法，对地物点进行规则网格化，认为当网格内最高点满足安全距离要求时，该网格内不存在隐患点，跳过该网格内其他地物点的隐患判断计算，以达到加快检测效率的目的。但对于高大树木、建筑而言，导线可能位于侧方而非上方，此时该方法易导致隐患点漏检。本文在该方法的基础上引入球体包含原理，采用严密的数学原理来对网格内地物点是否存在隐患可能性进行判定，以避免高大树木、建筑隐患点漏检的问题，如图5所示。

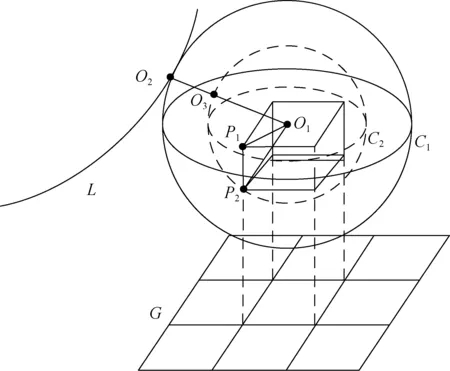
图5 基于球体包含原理的隐患点可能性判定示意Fig.5 Schematic diagram of potential hazard point determination based on sphere inclusion principle

如图5所示，格网G为线路通道划分的平面格网，曲线L为电力线，现格网G内任意方格的最高点O1，其与电力线L的距离最近点为O2，最近距离为d12，可得以点O1为球心，d12为半径构建的实线球体C1，可得C1区域中不含有电力线。

在O1、O2所在直线上取一点O3，O3与O2之间的距离d23设置为电力线安全距离阈值，此时以点O1为球心，以d12-d23为半径构建得到虚线球体C2。由求体包含原理可知，C2区域内任意点到C1区域外任意点的距离均大于d23，因此C2区域内的地物点均满足安全距离要求，无隐患可能。

为了便于网格内其他相对低的地物点进行隐患可能判断，在球体C2内取投影与平面网格一致的最大内切长方体，如图5中实线长方体所示。P1为网格内最大平面距离点，P2为长方体与球体C2的内切点，在进行其他相对低的地物点隐患可能性判断时，仅需要与内切点P2的高程进行比较，当地物点高程大于P2时，该点位于内切长方体内，无隐患可能。以单个塔段为例，具体步骤如下：

步骤1：坐标变换，将输电线路通道地物点由原有坐标(x,y,z)转化为线路走廊坐标(u,v,z)，线路走廊平面坐标系如图6所示。点A为小号杆塔中心桩、B为大号杆塔中心桩，P为AB通道内任意一点，u为AP连线在AB上的投影距离，v为点P到与AB平行且在线路前方向右侧50 m处直线的垂直距离，u、v的具体计算参照三角形原理。

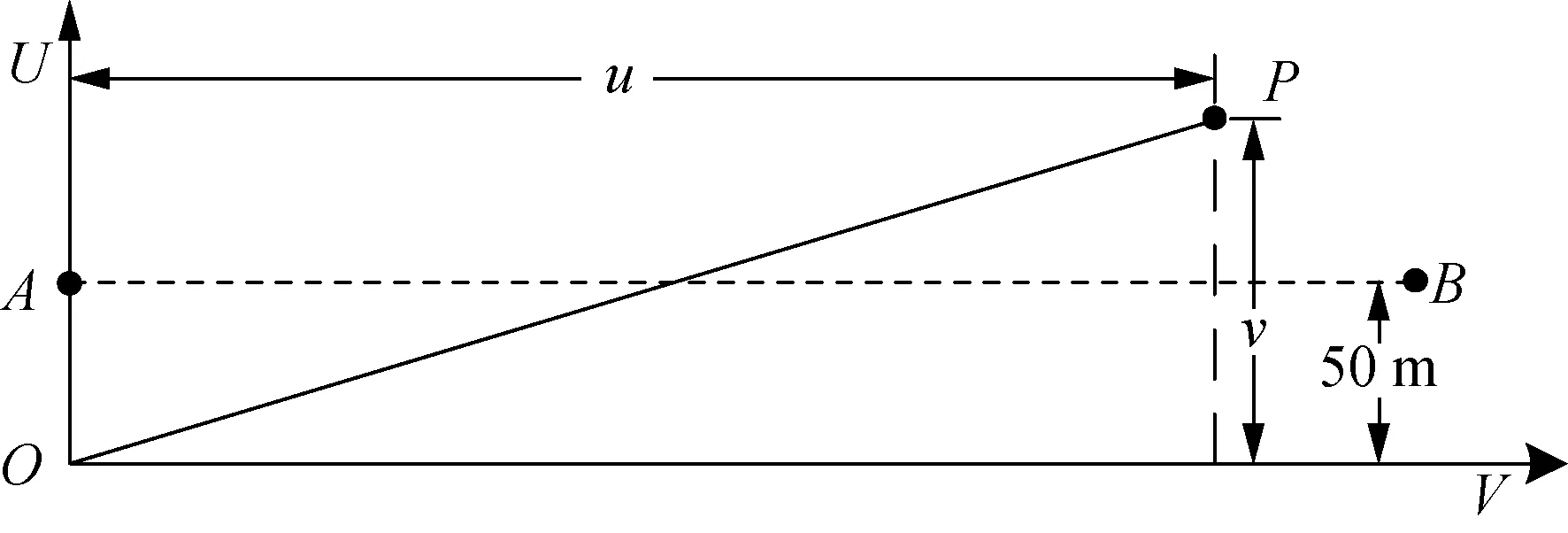
图6 线路走廊平面坐标系示意图Fig.6 Schematic diagram of line corridor plane coordinate system

步骤2：将地物点按高程z值从高到低进行排序，并按地物点类别进行归类，得到各类地物点的点集集合{PC1,PC2,…,PCn}，n为地物点的类别格式。

步骤3：令j=1。

步骤4：点集PCj含有mj个点，对应种类的地物点到电力线的安全距离阈值为τj。

步骤5：令k=1，建立网格对应的高程矩阵H，其行数为100，列数为LAB+1，LAB为A、B之间的平面距离，由于地球上任意点高程值不超过10 000 m，因此矩阵H内各元素初始设置为10 000。

步骤6：隐患可能性判断，点Pk为集合PCj中第k个点，根据Pk的坐标(uk,vk,zk)，其所在方格的行号为[vk]，列号为[uk]，其对应的高程限差为zmin=H[vk]×[uk]。若zk>zmin，则该点无隐患可能，进行步骤10；反之则进入步骤7进行隐患检测。

步骤7：隐患点判定，通过点到电力线离散点集的最近点搜索，计算出点Pk到电力线的最近距离为dk。若dk≤τj，则点Pk为隐患点，加入隐患点集，进行步骤10；反之进行步骤8来更新网格对应的高程限差。

步骤8：计算点Pk到其所在方格四边的最大平面距离ηk，计算公式如下：

(3)

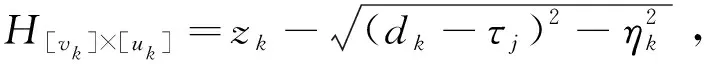
步骤10：令k=k+1，若k≤mj重复步骤6；反之进行步骤11；

步骤11：令j=j+1，若j≤n重复步骤3；反之则算法运行结束。

算法流程如图7所示。

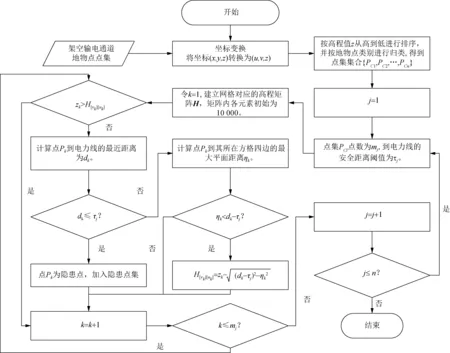
图7 通道隐患快速检测算法流程图Fig.7 Flow chart of channel hidden danger fast detection algorithm

2 实验分析

为了验证上述算法的有效性，本文对算法中电力线离散点集化、通道隐患检测两个阶段进行了对比实验。

2.1 电力线空间曲线离散点集化对比实验

由于采样点之间存在一定的采样间隔，采用计算地物点到离散点集最近点距离的方式来解决点到电力线曲线最近距离求解问题，电力线上到地物点的最近点不可避免会偏移到其在离散点集中的最近采样点，产生最近点定位偏差。

为了验证等水平间隔采样方式与等线长间隔采样方式对最近点定位偏差的影响，本文采用档距、挂点高差以及设计冰厚均不一致的两档220 kV GIM电力线模型数据进行对比分析，并按照0.1 m的采样间隔分别按照等水平间隔、等线长间隔的采样方式进行采样得到电力线离散点集，GIM电力线详细信息与采样点数如表2所示。

表2 两档GIM电力线相关信息与采样点数Table 2 Relevant information and sampling points of two GIM power lines

从表1中可以看出，电力线1跨越档距较小、挂点高程相近且位于轻冰区，其设计线长与水平档距大致一致，用以表征普通输电线路的电力线分布；电力线2跨越档距较大、挂点高程悬殊且位于重冰区，其设计线长与水平档距存在较大差距，用以表征高山区、重大交跨等特殊档的电力线分布。

本文采用密集采样的方式来统计电力线各区域的最近点定位偏差，每隔0.001 m等水平间隔在电力线上取点视为地物点的最近点，分别计算其在等水平间隔、等线长间隔离散点集中的最近点定位偏差。为了便于展示分析，本文每5 m水平距离区间内统计一个最近点定位偏差最大值作为区域最近点定位限差，两档GIM电力线的区域最近点定位限差随水平距离分布如图8所示。

从表2、图8中可以得出，等线长间距采样方式在表征普通输电线路的电力线分布的电力线1上采样点数、区域最近点定位限差与等水平间距采样基本保持一致，但在表征高山区、重大交跨等特殊档电力线分布的电力线2上表现出明显优势。如图8(b)所示，等水平间隔采样方式在电力线2上区域最近点定

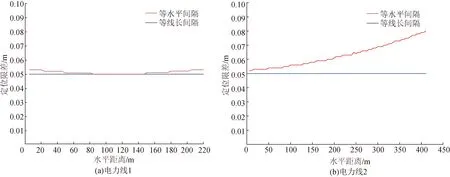
图8 两档GIM电力线的最近点定位限差分布图Fig.8 Distribution diagram of maximum value of nearest point positioning deviation of two GIM power lines

位限差达到0.08 m左右，然而等线长采样方式仍能够保持在0.05 m左右。

为了进一步分析最近点点位偏差的分布规律，在电力线2上截取了等水平间隔采样方式下定位限差最大与最小的两个区域最近点定位偏差数据，如图9所示。

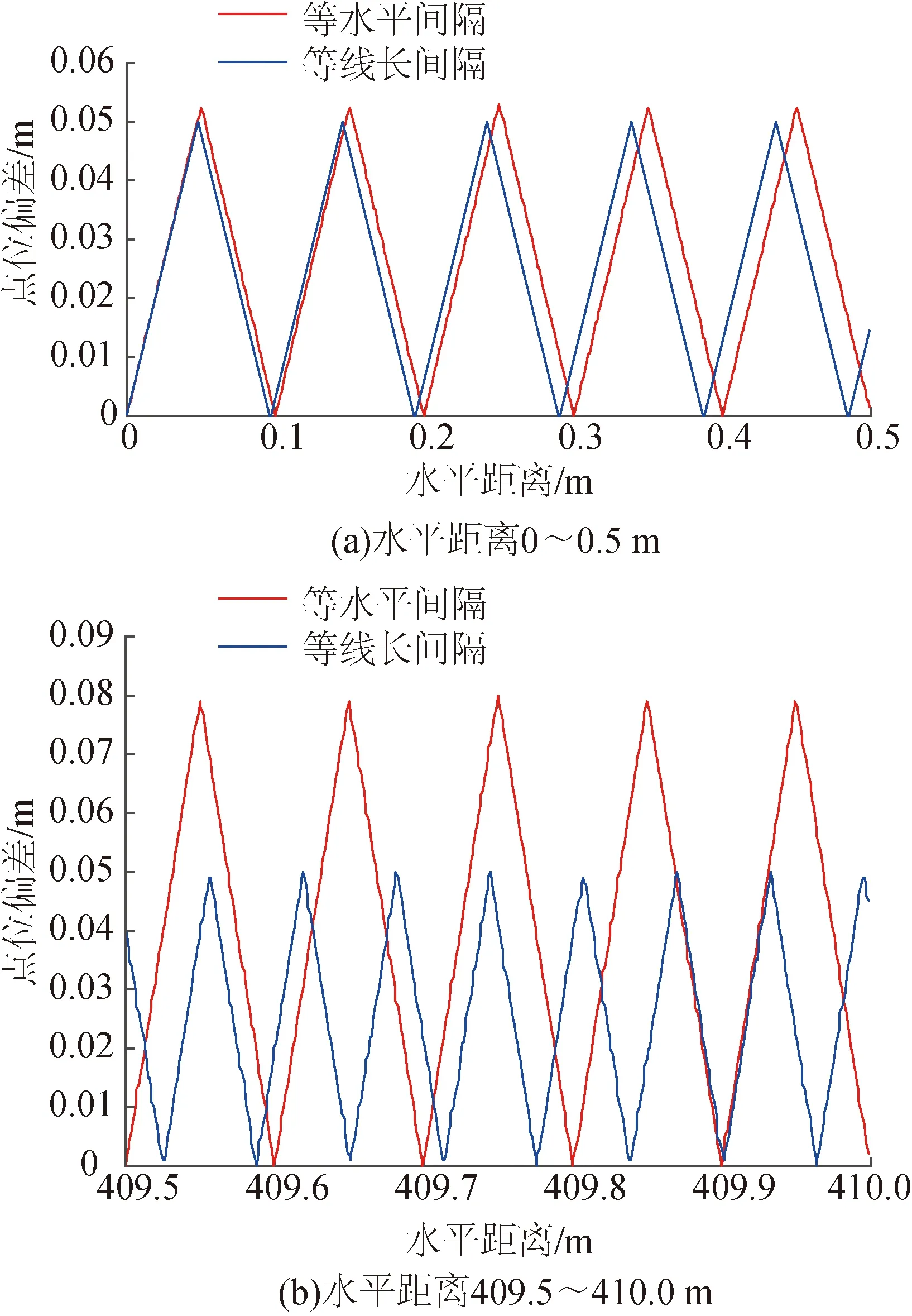
图9 区域最近点定位偏差分布图Fig.9 Distribution map of regional nearest point positioning deviation

从图9中可以得出，等水平间隔采样与等线长采样两种方式最近点定位偏差均符合0到区域最近点定位限差之间均匀分布，而区域最近点定位限差由区域采样点之间的线长间隔决定。从图9(a)与图9(b)对比中可以看出，对于跨越档距较大、挂点高程悬殊的特殊档等水平间隔的采样点在电力线上分布并不均匀，局部区域的线长间隔差异大，导致区域最近点定位限差达到设计的1.5～2.0倍，不利于精度控制。而等线长间距采样方式无论在档距较小、挂点高程相近的普通档以及跨越档距较大、挂点高程悬殊的特殊档均能够保证采样点分布均与，将最近点定位限差控制在目标范围内。

2.2 架空输电线路通道隐患检测对比实验

为验证本文通道检测算法的应用效果，选取某一220 kV架空输电线路GIM模型中连续50档数据进行通道隐患检测，地物点数据通过激光雷达系统进行采集，各档地物点统计如图10所示。

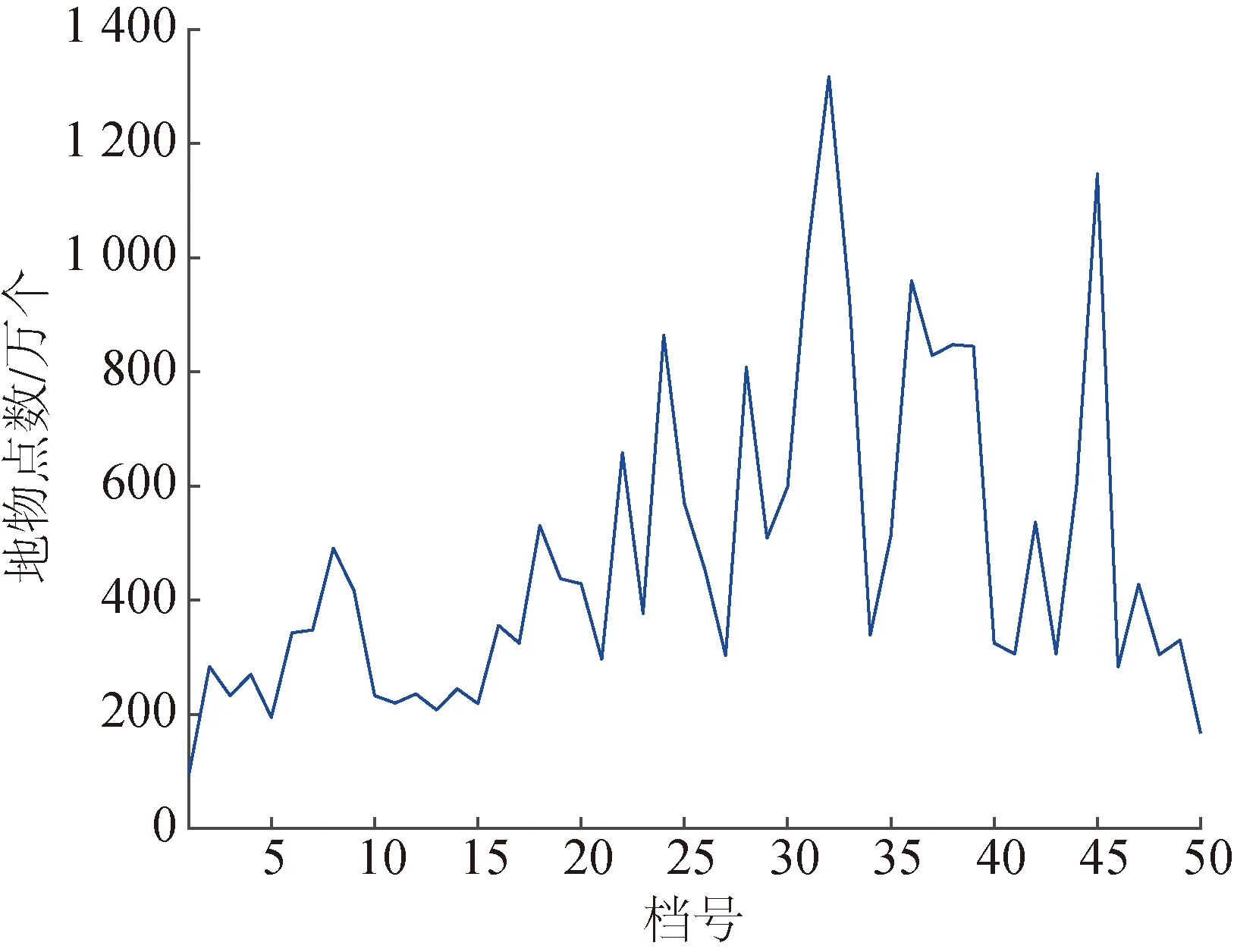
图10 50档地物点点数统计Fig.10 Statistical chart of 50 ground feature points

基于GIM模型电力线采用等线长间隔采样后得到电力线离散点集后，分别按照传统逐点检测、网格法过滤以及本文方法进行隐患检测，分别对检测速度以及检测结果进行对比分析，如图11所示。

从图11中可以看出，网格法与本文方法在检测效率上较传统逐点检测均有较大提升，各档隐患检测耗时缩短为原本耗时的1/20到1/8。根据统计，50档通道检测逐点检测耗时1 169 s，而网格法耗时94 s，为逐点检测耗时的8.0%；本文方法耗时80 s，为传统逐点检测耗时的6.9%。

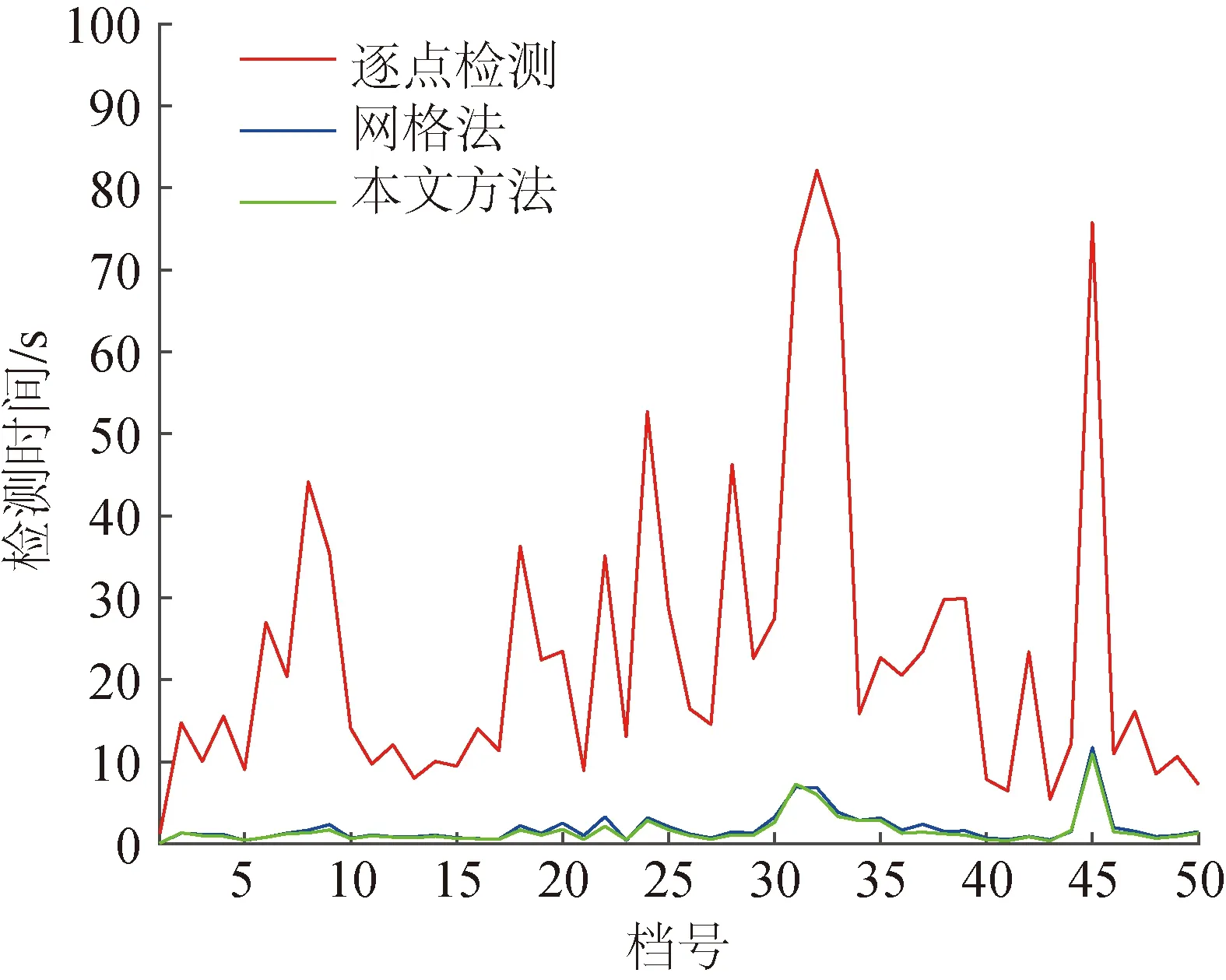
图11 3种隐患检测方法检测耗时对比Fig.11 Comparison of detection time of three hidden danger detection methods

表3为3种通道隐患检测方法检测出的隐患点数统计情况，表中标红部分的网格法检测结果与其余两种方法检测结果并不一致，存在漏点情况。而本文方法从表3中可以看出，各档检测结果仍与逐点检测保持一致，在大大提升检测效率的同时，保证检测结果正确性。

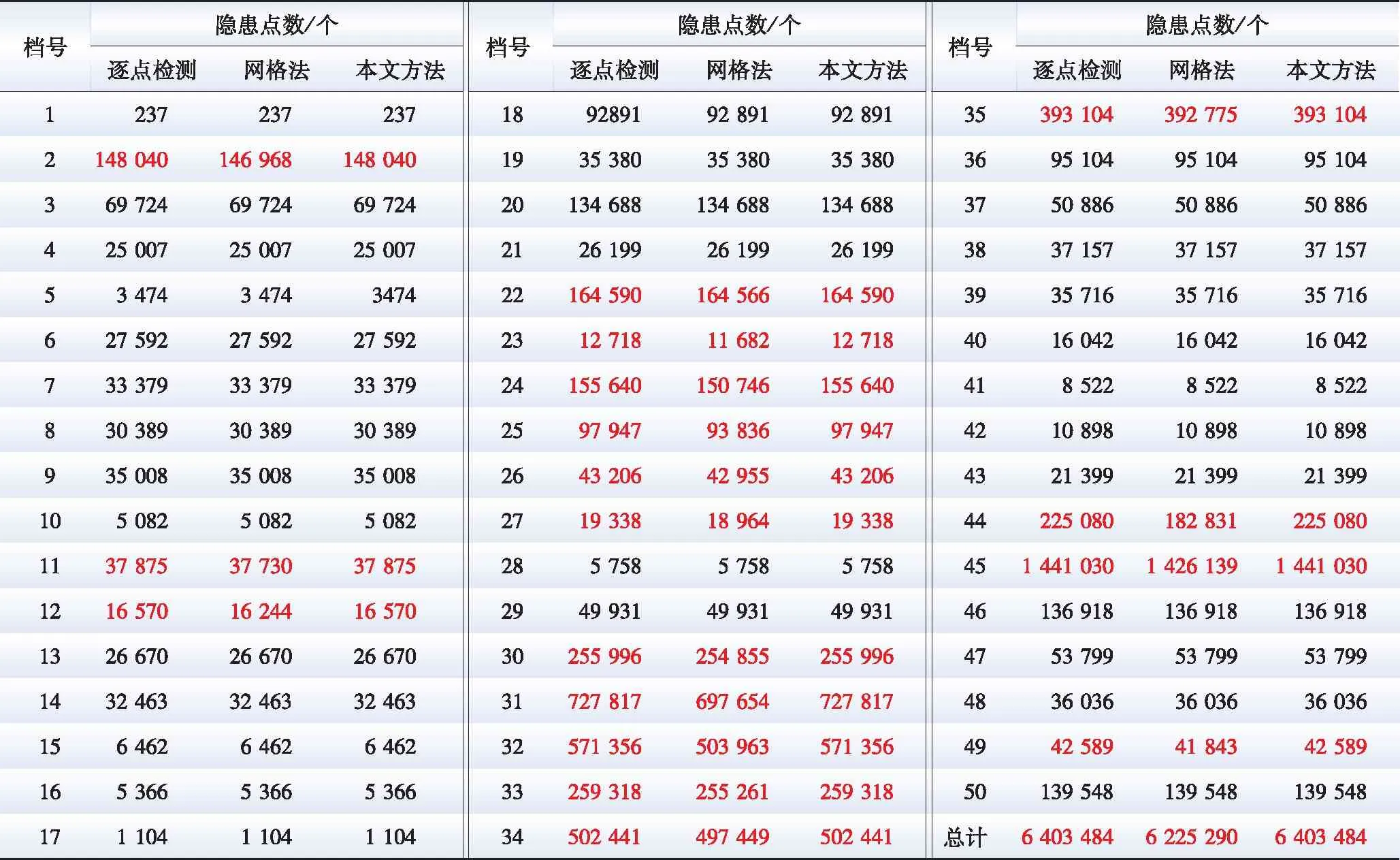
表3 通道隐患检测隐患点数统计Table 3 Statistics of hidden danger points of channel hidden danger detection

为进一步阐述本文方法与网格法检测的差异性原因，截取了本文方法与网格法隐患检测结果不同处的点云场景，如图12所示。

图12中白色点为电力线离散点、蓝色点为地面点、绿色点为植被点、红色点为通道隐患点。由俯视角、侧视角对比可知，当导线从高大树木侧方通过时，由于侧方地物高点满足安全距离要求，网格法认为地物高点所在网格无隐患可能，跳过最近距离检测导致漏检。而本文提出的基于球体包含原理采用更为严密的隐患判断依据，针对侧方高大地物情况仍能够保证正确的检测结果。

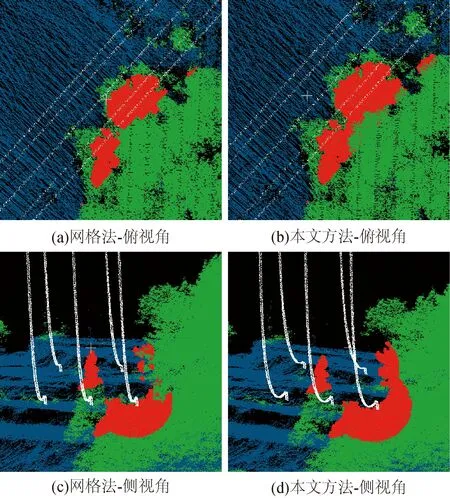
图12 本文方法与网格法隐患检测结果对比Fig.12 Comparison of hidden danger detection results between this method and grid method

3 结 论

本文提出了一种基于等线长点集化和球体包含原理的通道隐患快速检测方法，在保证隐患检测精度的基础上实现通道隐患检测速度。

1)提出了基于等线长间隔的GIM电力线离散点集方法，将电力线局部区域视为空间直线分布实现线长间隔到水平间隔的改正计算，克服现有等水平间隔采样离散点集在电力线上分布并不均匀，跨越档距较大、挂点高程悬殊特殊档最近点定位偏差增大的问题。

2)针对网格法检测速度优化算法存在漏检问题，在该方法的基础上引入球体包含原理，采用严密的数学原理来对网格内地物点是否存在隐患可能性进行判定，以避免高大树木、建筑隐患点漏检的问题。

3)经实验验证，本文提出的等线长间隔采样方法无论在档距较小、挂点高程相近的普通档以及跨越档距较大、挂点高程悬殊的特殊档均能够保证采样点分布均匀，将最近点定位限差控制在目标范围内；基于球体包含原理的隐患快速检测方法能够在保证检测精度的前提下将隐患检测耗时优化为原本耗时的6.9%。