不同工况下功率型锂离子电池的热特性与仿真研究

胡言庆，杨 斌，王宇作，杨 军，刘登锋，阮殿波

(1.宁波大学机械工程与力学学院，浙江 宁波 315211；2.宁波大学先进储能技术与装备研究院，浙江 宁波 315211；3.合盛新能(宁波)科技有限公司，浙江 宁波 315040)

1 引言

“十四五”规划期间，锂离子电池作为国家重点发展产业，在环境保护和能源供应上发挥了关键作用。因其在能量密度、稳定性、使用寿命等方面突出的优势[1]而成为新能源汽车、智能电网、航空系统、轨道交通等领域的核心部件[2]。在“绿色化”、“智能化”的时代发展需求下，充电速度更快、循环寿命更长的功率型锂离子电池成为了下一阶段锂离子电池的重点研发方向。但是，由于功率型电池在充放电过程中不可避免地会存在充放电电流大、使用次数频繁、散热不及时等恶劣工况，严重加剧了电池的热失控风险。因此对功率型锂离子电池单体的热行为进行研究显得尤为重要，同时也能为电池温度预测及电池系统产热分析提供重要依据[3]。

采用电热耦合模型对锂离子电池的热行为进行研究是行之有效的方法，而精确电学模型的建立则是关键。电学模型包括电化学热模型、等效电路模型 (Equivalent Circuit Model，ECM) 及黑箱模型三种。其中，等效电路模型具有参数直观、适用性高及参数辨识性强等优点，应用最为广泛[4]。当前，等效电路模型已发展出了Rint模型、Thevenin模型、双极化(Dual Polarization，DP)模型等[5]。上述模型在模拟精度、计算量、参数识别难度等方面存在各自的优缺点，在实际应用中需要进行良好的权衡。其中，Rint模型计算简单，但忽略了电池内阻动态特性，精度不高；Thevenin模型计算简单，且具有一定的适用性；DP模型则是在Thevenin模型上，加入了一个RC阻容电路，计算复杂，但能更准确反映内部各项内阻的变化响应特性[6]。

基于上述各模型特性，本文对Rint模型、Thevenin模型与DP模型进行了多参数的优化分析，并将电学模型输出的内阻参数进行计算，借助Bernardi生热速率[7]公式对电池的热行为进行了研究。此外，借助混合功率脉冲特性 (Hybrid Pulse Power Characterization，HPPC)工况测试，依据Rint模型、Thevenin模型和DP模型，探讨了在不同环境温度和电流下电热耦合模型的内阻参数变化规律，对比分析了不同工况下电热耦合模型的可靠性。

2 模型方法

2.1 电路模型

建立基于放电倍率Crate、温度T及荷电状态SOC的Rint模型、Thevenin模型与DP模型，能更精确模拟在不同工况电流I下电池内部参数的变化。三种电路模型如图1所示。

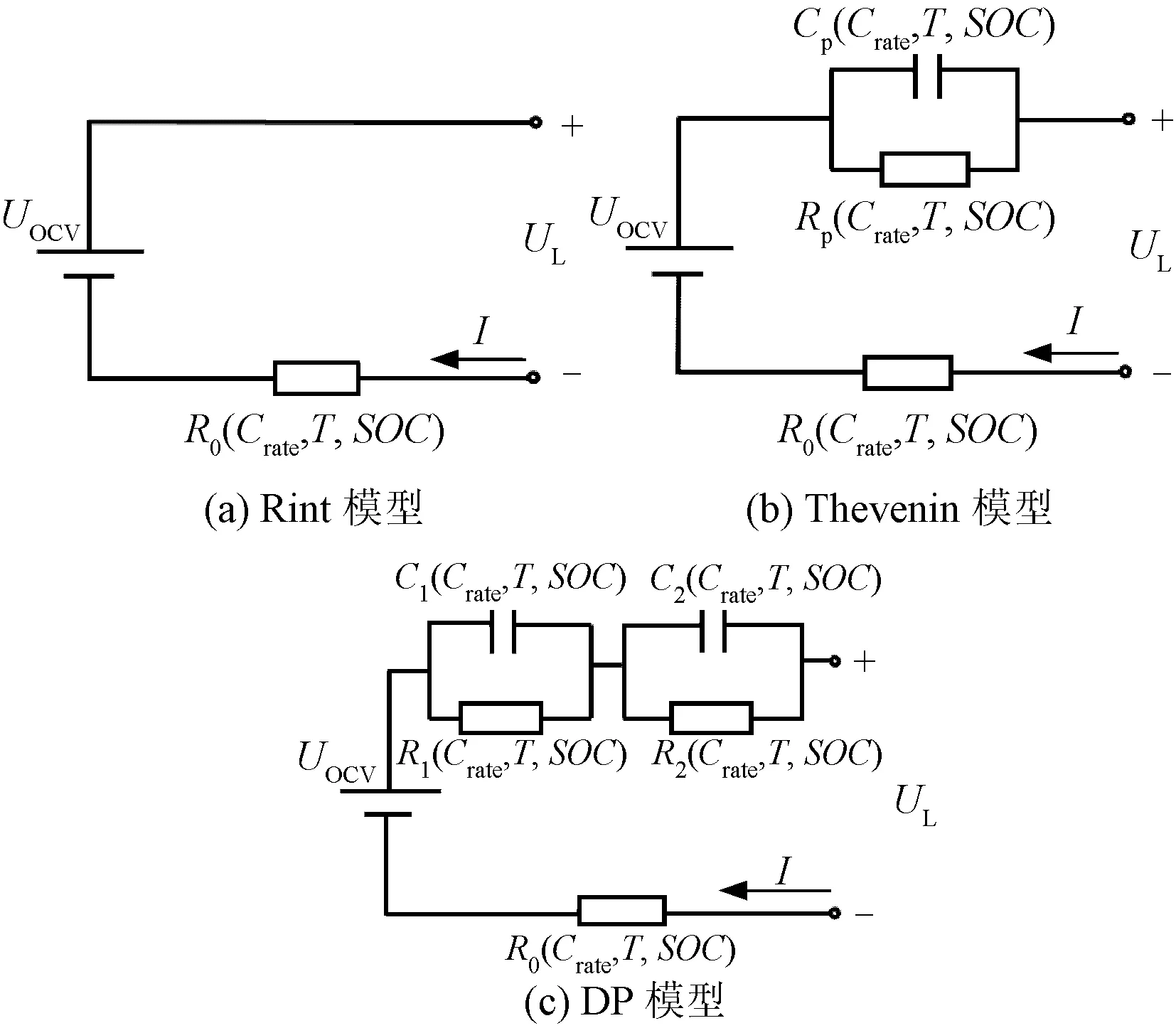
图1 三种不同电路模型Fig.1 Three different circuit models

三种电路的数学模型分别如式(1)～式(3)所示:

(1)

(2)

(3)

式中，UL为电池两端电压；UOCV为电池开路电压；U1、U2分别为电化学极化、浓差极化电容的端电压；R0、Rp分别为电池的欧姆、等效极化内阻；Cp为电池的等效极化电容；R1为电化学极化电阻；C1为电化学极化电容；R2为浓差极化电阻；C2为浓差极化电容。

2.2 生热模型

根据牛顿热力学定律，锂离子电池产生的总热量主要用于电池自身生热量与同外界对流交换的热量，其中电池自身产生的热量由焦耳热以及可逆热组成[8]。

(4)

式中，Qa、Qgen、Qconv、Qj和Qe分别为电池产生的总热量、自身的化学热、与外界交换热、焦耳热和可逆热；m为电池的质量；Cb为电池的比热容；h为电池与外界对流换热系数；s为电池与外界对流换热面积；Ts、T分别为电池表面温度、电池周围环境温度。其中，电池产生的焦耳热Qj主要与电池的等效内阻Re以及电流I相关，可逆热Qe受温熵系数dU/dT、电流I及温度T的影响[9]，具体计算如式(5)所示：

(5)

在生热模型中，生热量与放电倍率有关。当电池放电倍率≥1 C时，电池内部电化学反应产生的可逆热远小于电池内部的欧姆热，且随着放电倍率增大，可逆热占比越小[10-12]。因测试倍率均已高于1 C，为优化生热模型，忽略可逆热并采用均一化模型，即电池生热模型中的产热速率函数可近似为：

(6)

式中，q为电池的产热速率；V为电池体积。

2.3 电热耦合模型

电池的温度影响电路模型，电路模型也直接作用于电池的生热模型，二者相互影响，相互作用，形成电热耦合模型，如图2所示。其中，耦合模型的输入参数为电流I与环境温度T，通过电路模型与生热模型中相关参数计算，最终计算出电池表面温度Ts。

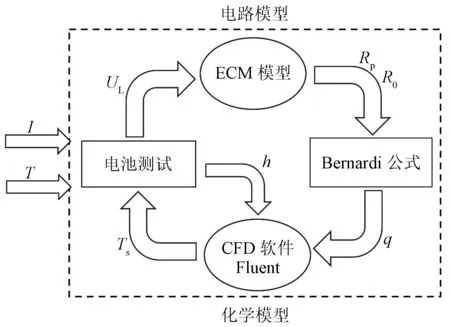
图2 电热耦合模型框架Fig.2 Electrothermal coupling model framework

3 参数辨识

3.1 实验对象

本文以合盛新能(宁波)科技有限公司产的功率型圆柱型锂离子电池21700为实验对象，电池的基本参数见表1。

表1 功率型圆柱型锂离子电池21700基本参数Tab.1 Basic parameters of power type 21700 cylindrical lithium-ion battery

采用上海恩智测控技术公司的充放电测试仪(NGI-N5600A)对电池进行充放电测试，上海晶齐实业公司的多路温度测试仪(AT4716)对电池表面温度进行监测，上海衡鼎仪器设备厂的高低温试验箱(HDGDWJ-18)提供了电池不同环境温度。

3.2 内阻参数辨识及分析

在5 ℃、15 ℃、25 ℃、35 ℃的环境温度以及1 C、2 C、3 C、4 C的放电电流下，本文对实验对象进行了不同SOC的HPPC测试，即对不同SOC下的电池进行倍率脉冲实验，其中充电与放电时间为10 s，搁置时间为40 s，为保证不同SOC下稳定性，不同倍率下测试的搁置时间需大于0.5 h，确定并选取10%～90%的SOC为测试区间。为确保实验的准确性，在SOC下降10%[13]后进行搁置1 h处理。其中，测试中电压电流响应变化如图3所示。

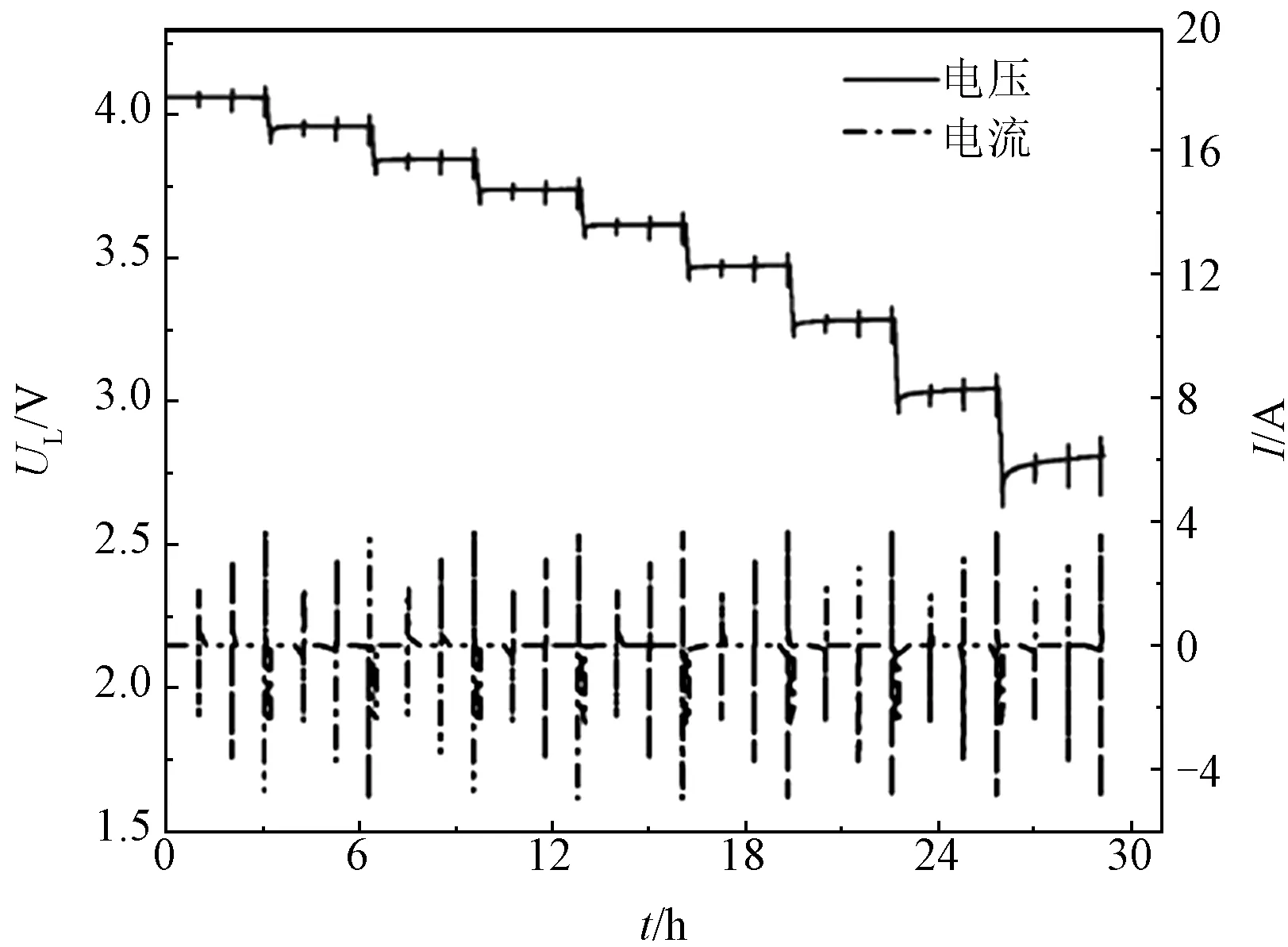
图3 HPPC测试下电压、电流响应曲线示意图Fig.3 Voltage and current response schematic under HPPC test conditions

其中，Rint模型、Thevenin模型与DP模型中的内阻参数R0、Rp、R1与R2可通过图3中HPPC测试下的电压与电流变化进行参数求解[14,15]，具体计算如式(7)、式(8)所示。

(7)

(8)

式中，ΔU1、ΔU2分别对应不同SOC下欧姆内阻R0与极化内阻Rp的响应电压变化值；Idis为不同SOC下的HPPC中脉冲放电电流；τ1、τ2分别为电化学极化电阻R1、浓差极化电阻R2对应的时间常数，并且与电化学极化电容C1、浓差极化电容C2在数值上存在τ=RC的关系。

通过上述计算后，模型识别出的各项内阻参数与环境温度T、放电工况的倍率Crate、荷电状态SOC的关系如图4与图5所示。

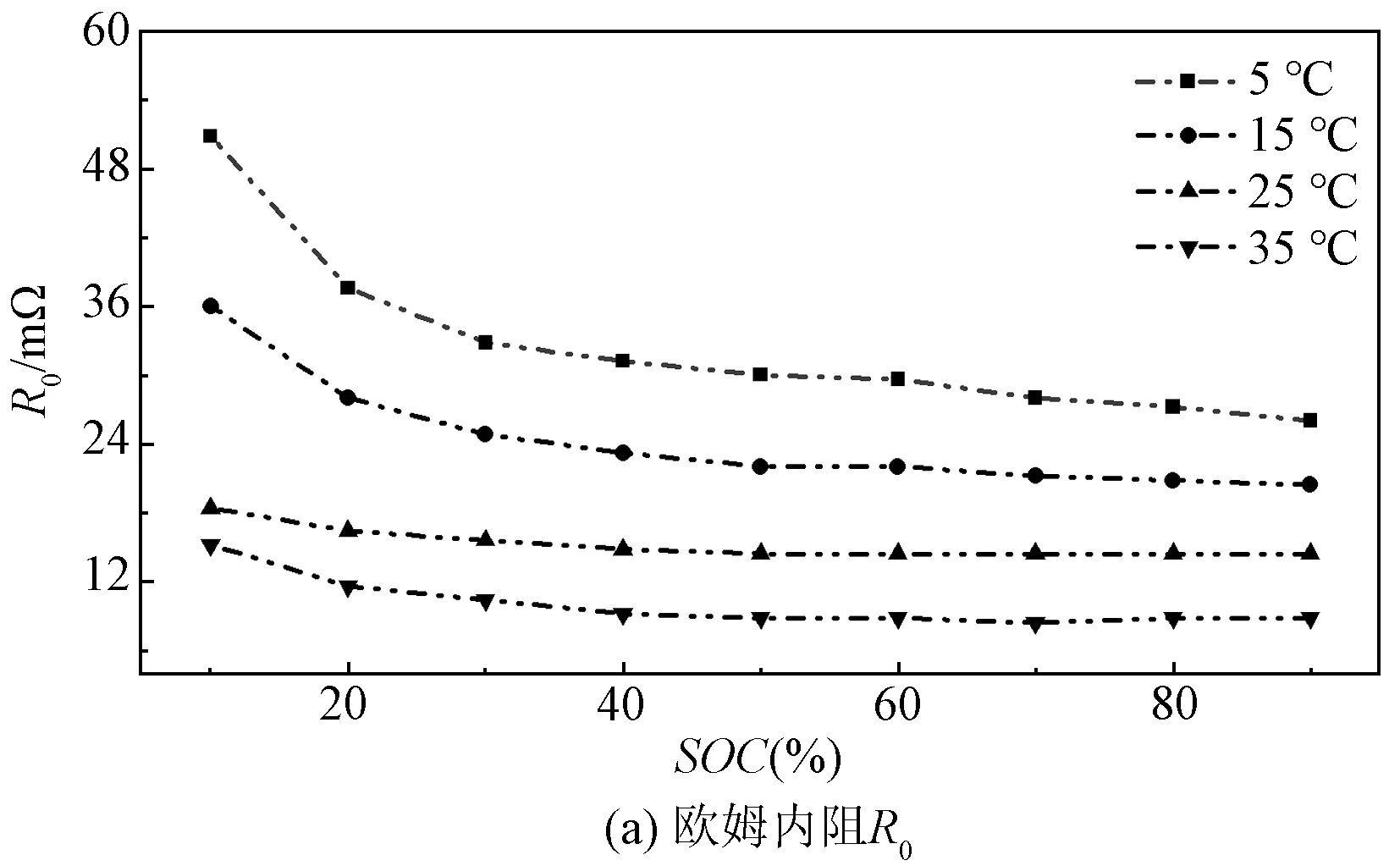
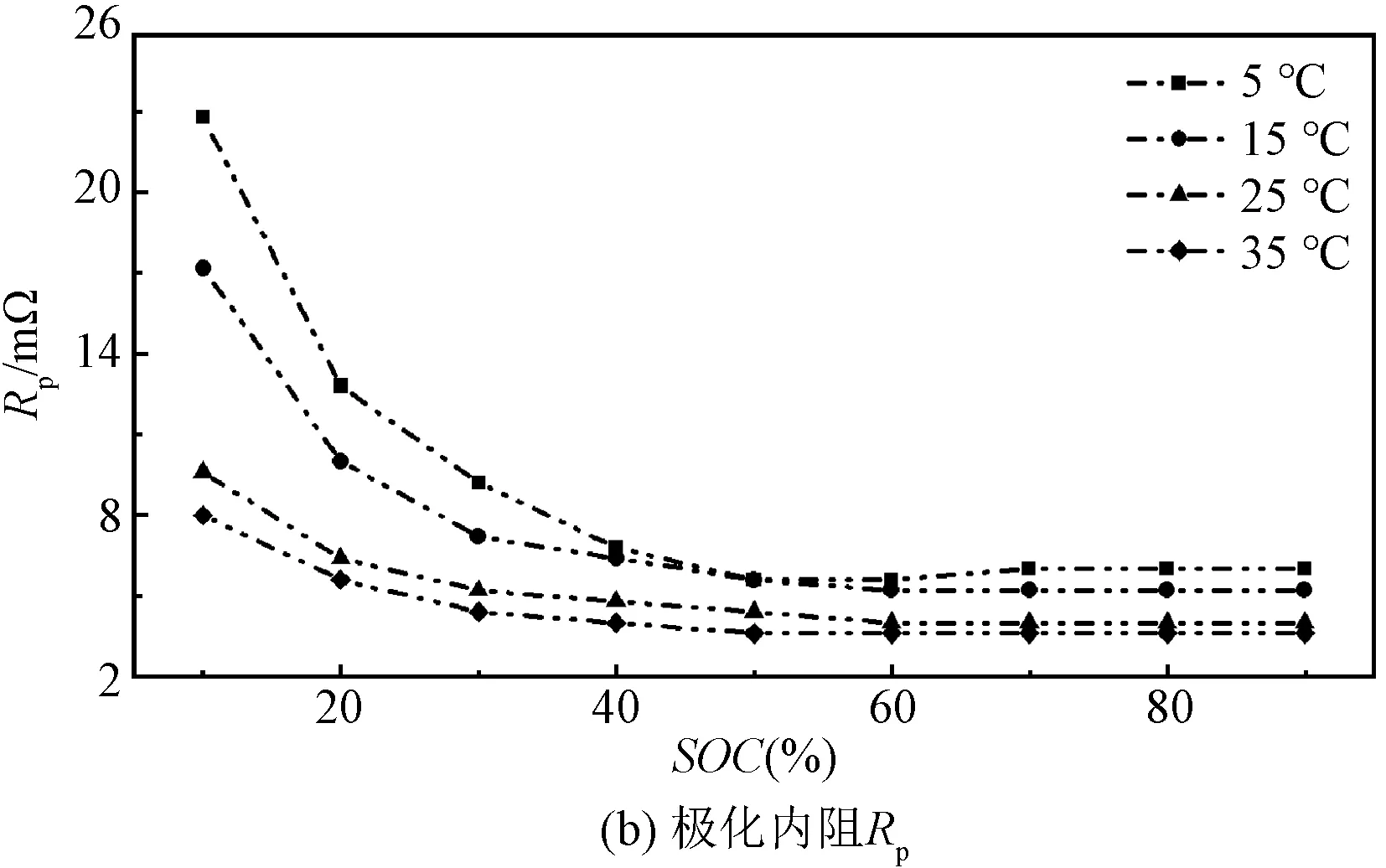
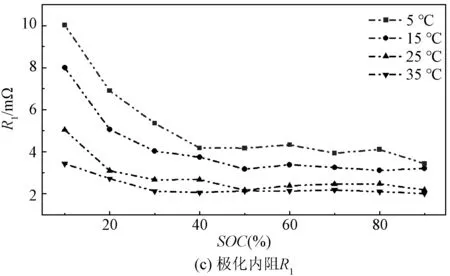
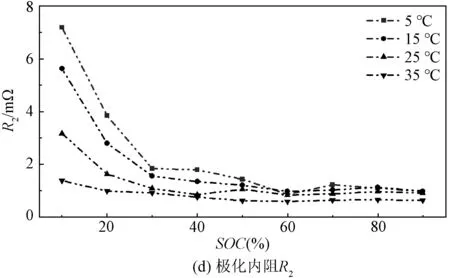
图4 1 C放电倍率不同温度下各项内阻变化Fig.4 Different ambient temperatures variation of resistance under 1 C discharge conditions

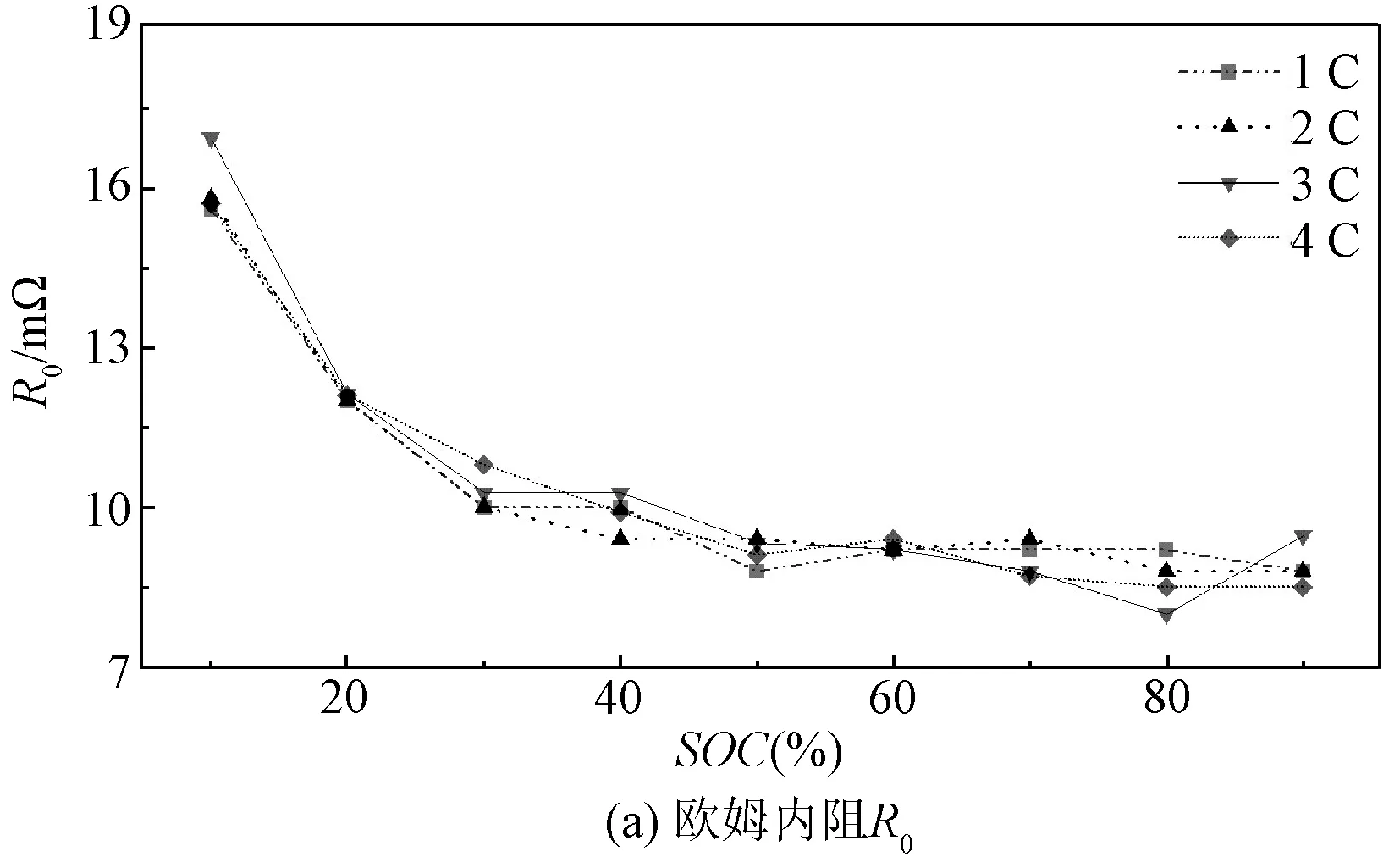
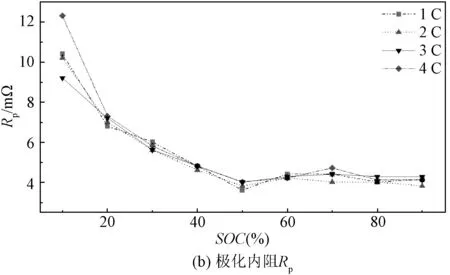
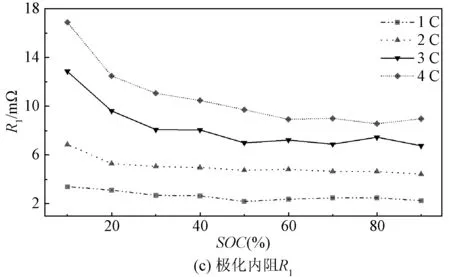
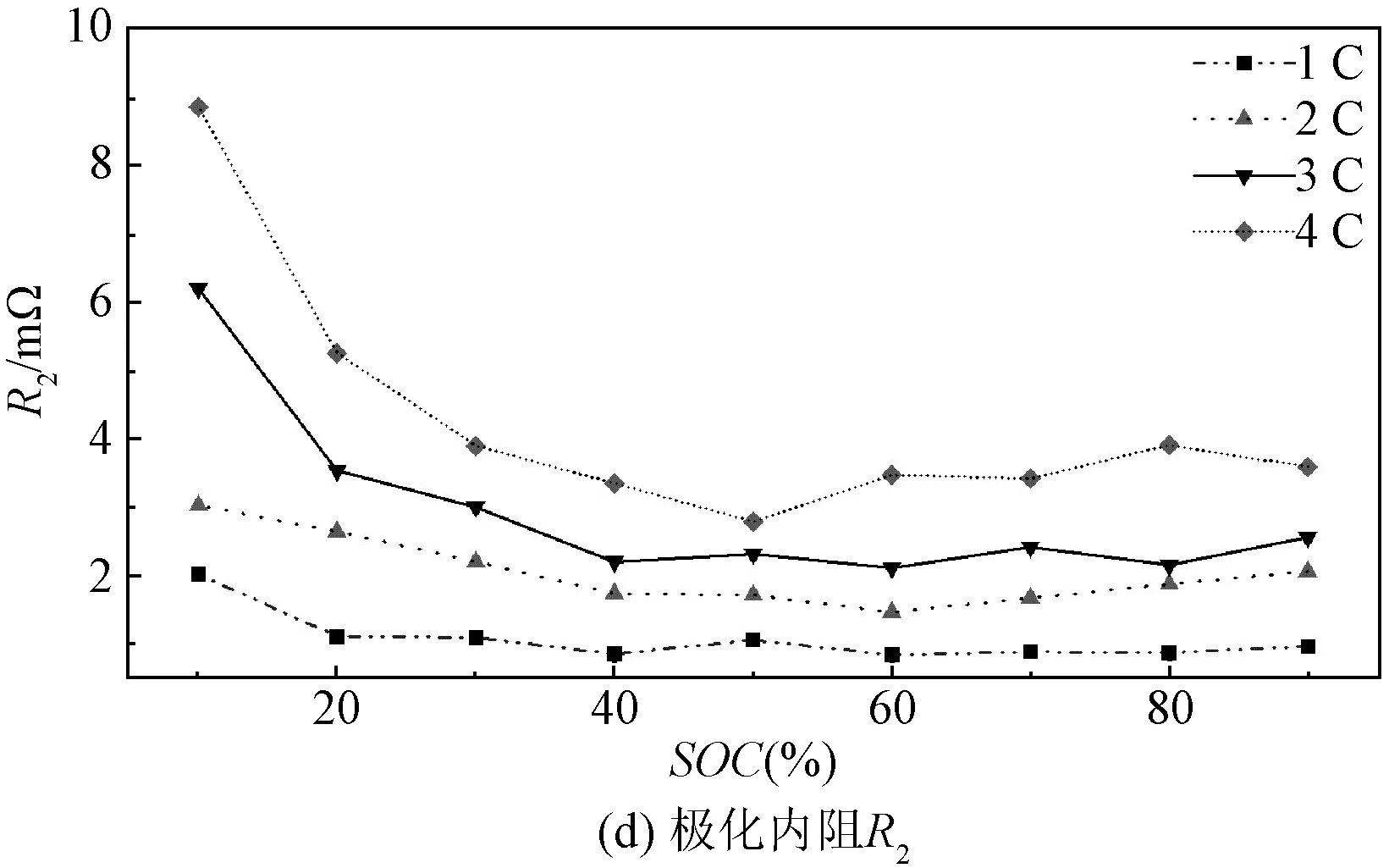
图5 常温不同放电倍率下各项内阻变化Fig.5 Different discharge rates variation of internal resistance under ambient temperature conditions

由图4、图5可知，在HPPC测试下，温度、放电倍率对模型中的电池内阻值R0、Rp、R1与R2的影响随SOC变化趋势一致。环境温度越低时，锂离子传输速率越低，电池内阻越大。且SOC越低时，电池内阻越高，因为此状态下正极表面的锂离子处于饱和状态，无法与电子结合，过多的锂离子聚集[16]。同时，随着放电倍率增大，Rint模型中的欧姆内阻R0和Thevenin模型中的极化内阻Rp变化较小，DP模型中极化内阻R1、R2会随着放电倍率的增大而增大。

3.3 电池热模型参数及换热参数分析

本文采用的功率型锂离子电池，内部电芯为全极耳卷绕式结构，内部材料由正负极活性材料、铝箔、铜箔、电解液与隔膜等组成。因此在导热系数上具有各向异性，可通过热阻串并联公式[17]计算各方向的系数，如式(9)所示：

(9)

式中，λx、λy、λz分别为电池内部x、y、z方向的导热系数；Li为电池内部各项材料的厚度；λi为电池内部各项材料的导热系数；L为电池内部材料厚度总厚度。

电池的密度以及比热容可采用加权平均方式进行计算，如式(10)所示：

(10)

式中，ρb为电池的密度；Vi为内部各项材料所占体积。

通过式(10)计算，得出功率型锂离子电池21700的热模型基本参数见表2。

表2 功率型锂离子电池21700各项热参数Tab.2 Thermal parameters of power lithium-ion battery 21700

根据能量平衡原理，电池表面的换热系数h与环境温度有关，通过放电后电池表面自然冷却相关参数可计算出电池表面的换热系数[18]。其中，在电池表面中间位置布置温度监测点，对不同工况下表面温度变化进行检测。假设电池表面的温度变化一致性较高[19]，根据式(11)计算出对流换热系数h。

(11)

式中，a为拟合系数。

通过Matlab工具对冷却实验曲线进行拟合，求解不同放电倍率下电池的对流换热系数h，分别为13.49 W/(m2·℃)、14.05 W/(m2·℃)、13.55 W/(m2·℃)、13.72 W/(m2·℃)。其中，温度冷却及拟合曲线如图6所示。

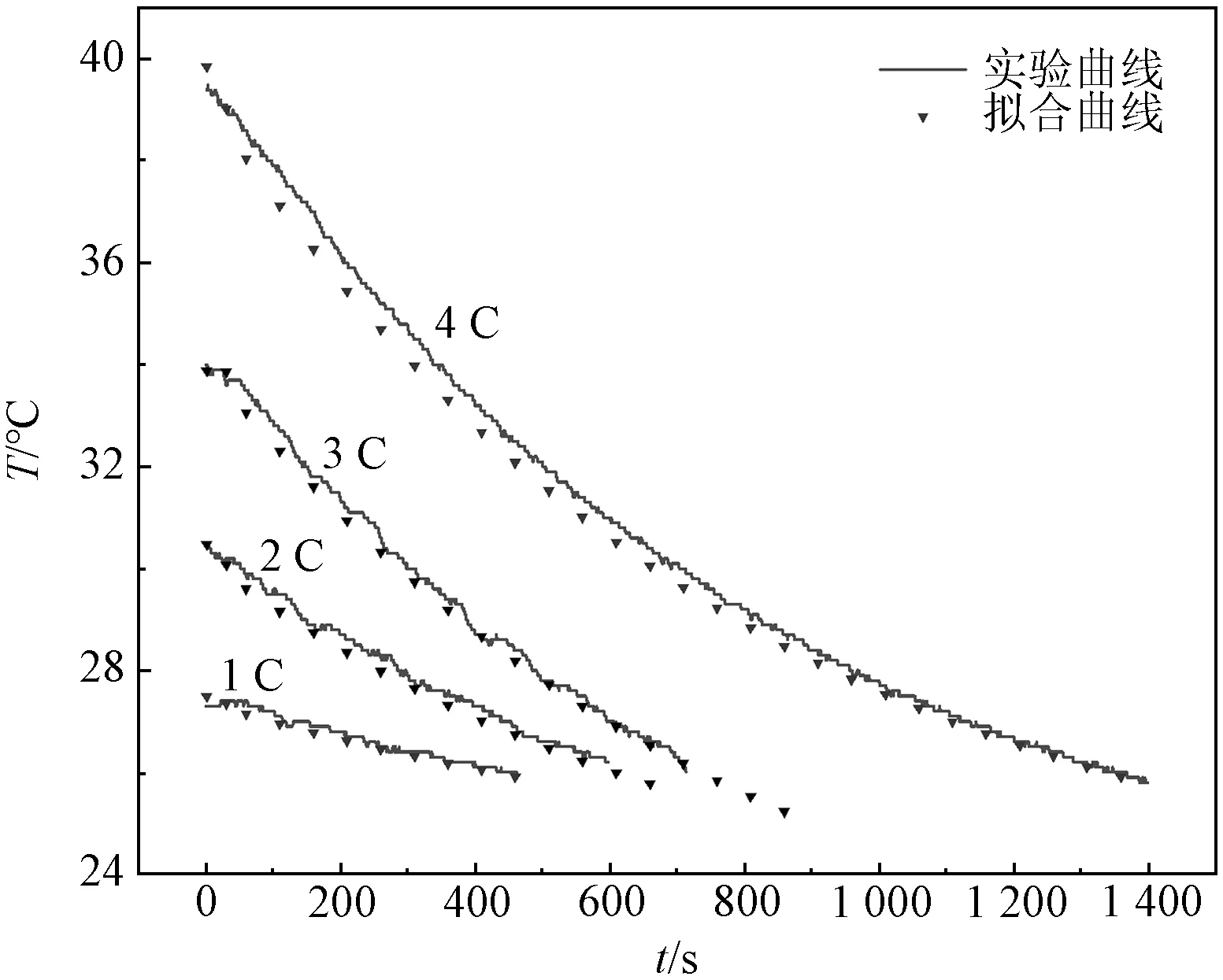
图6 不同放电倍率下电池冷却温度及拟合曲线Fig.6 Battery cooling temperature and fitted curve at different discharge multipliers

4 结果与讨论

4.1 生热模型仿真结果

采用多项式拟合的方式，对各项内阻参数的变化规律进行拟合。并将拟合求解的数值，通过生热计算后导入Fluent软件中，验证在1 C、2 C、4 C放电下三种模型的准确性。如图7所示，选取zy截面分析电池内部产热情况。其中，由于表面换热系数差距较小，模型在不同倍率放电截止时的温度分布相似。即电池最大温度分布于中心处附近，且在y靠近负极的方向上呈现递减状态，由于模型中负极换热面积大于正极，最终导致在电池负极处温度最低。

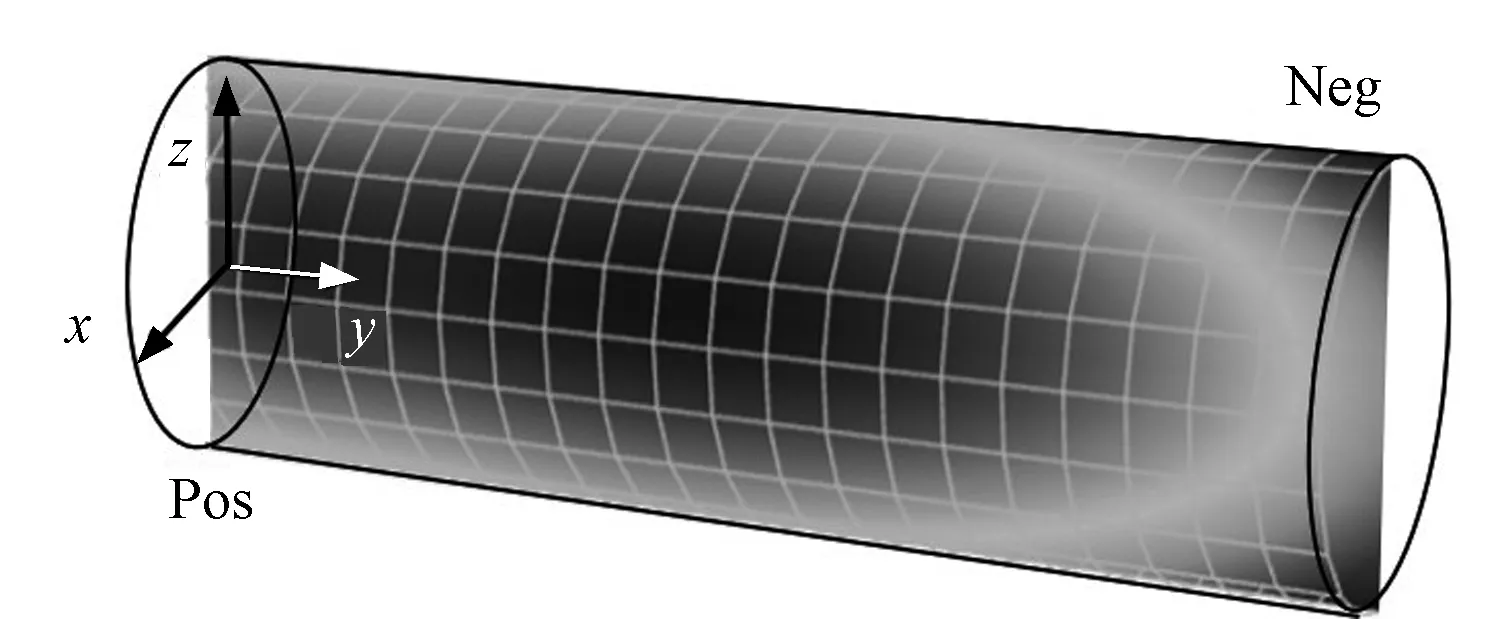
图7 电池温度截面图Fig.7 Battery temperature cross-section

4.2 生热模型精度对比

分别将1 C、2 C、4 C整个放电过程中的仿真与常温环境下的实验结果进行对比。其中，随着放电过程进行，温度误差逐渐增大。通过图8可知，当电池采用1 C放电时，DP模型与实验曲线拟合度最高；当电池采用2 C放电时，由曲线趋势可知，DP模型精度远高于Thevenin模型，且精度与Rint模型精度相差较小；当电池采用4 C放电时，Thevenin模型、DP模型与实验结果拟合较差，但Rint模型与实验结果拟合程度高，趋势较为相近。

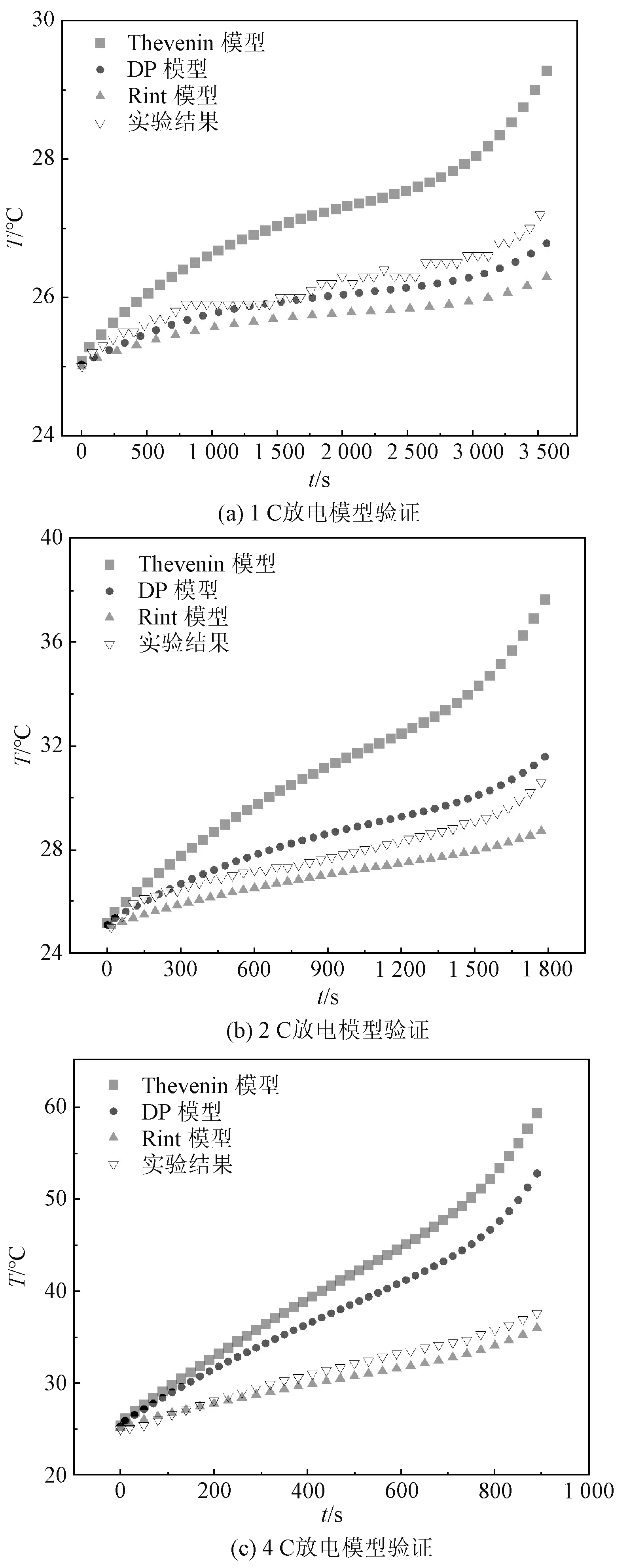
图8 不同放电倍率下模型的验证Fig.8 Validation of model at different discharge rates

为了定量地分析拟合精度，采用最大绝对误差(Maximum absolute Error，Max.E)、平均绝对误差(Mean Absolute Error，MAE)、均方根误差(Root Mean Square Error，RMSE)与平均相对误差绝对值(Mean Absolute Relative Error，MARE)四种误差来判断不同放电倍率下的Rint模型、Thevenin模型与DP模型的精度[20]。

根据图9误差对比可知，在1 C、2 C放电时，误差(Max.E、MAE、RMSE、MARE)最大与最小的模型分别为Thevenin模型和DP模型。其中，在1 C放电时，DP模型误差值分别为 0.58 ℃、0.18 ℃、0.21 ℃和0.68%，约为Rint模型的1/2、Thevenin模型的1/4，精度更高，表明DP模型更适用于电池1 C放电；在2 C放电时，DP模型误差值分别为1.04 ℃、0.68 ℃、0.77 ℃和2.4%，与Rint模型相比，仅在Max.E上存在1 ℃的差异，其他误差基本保持一致，表明DP模型更适用于电池2 C放电。但是，在4 C放电时，Rint模型的误差分别为1.83 ℃、0.81 ℃、1.06 ℃和3%，精度比其他模型高，同时数值与2 C放电时的误差相近，表明Rint模型更适用于电池4 C放电。

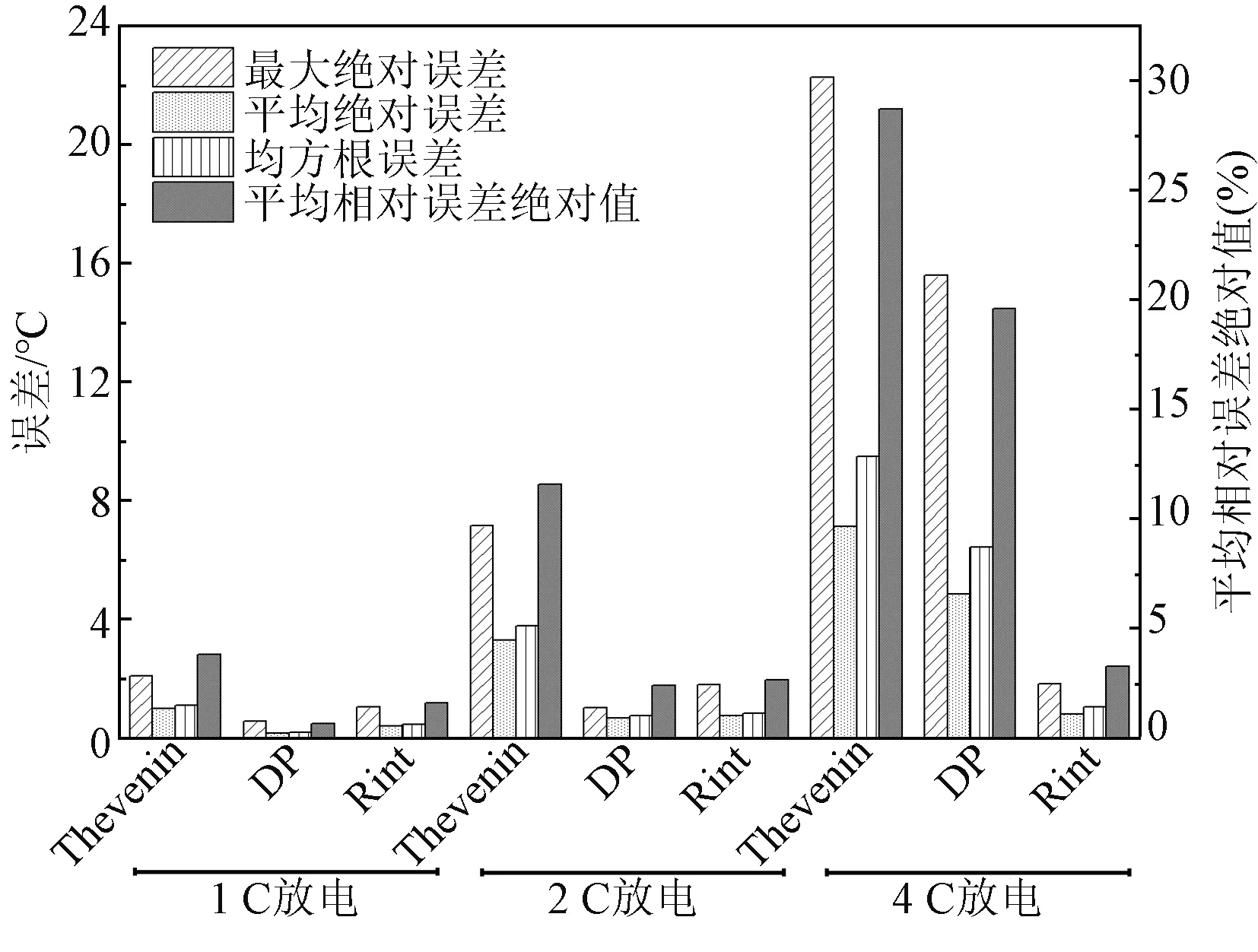
图9 常温不同放电倍率下模型误差的对比Fig.9 Different discharge rates comparison of model errors under ambient temperature conditions

4.3 高倍率验证

根据上述验证结果可知，Rint模型的精度与放电倍率相关。为验证更高倍率下该模型的精度，对电池进行常温环境下的8 C、10 C放电。其中，两种工况下仿真与实验的对比结果如图10所示。

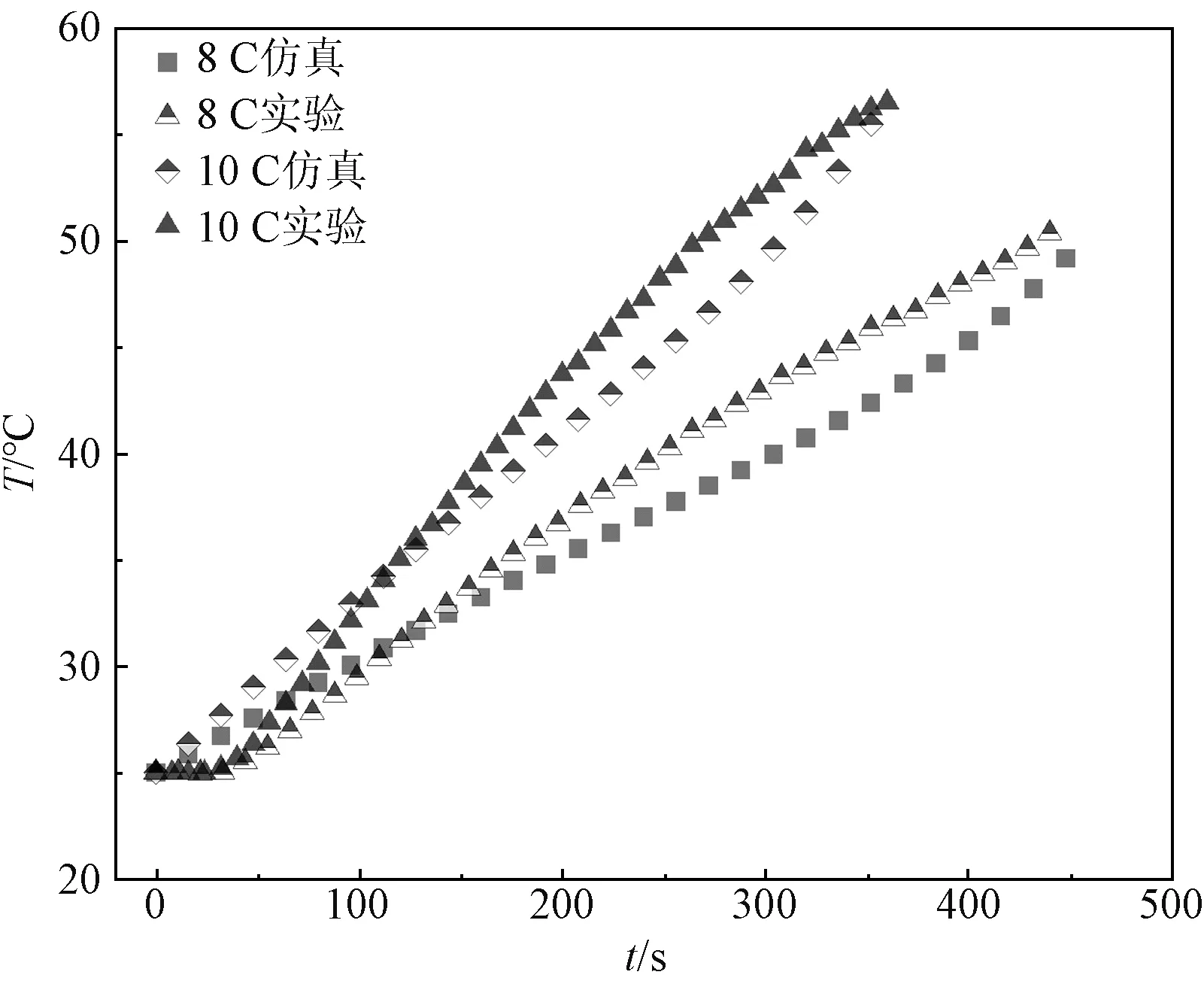
图10 高倍率下Rint模型验证Fig.10 Rint model validation under high discharge rate

通过验证结果可知，Rint模型在8 C、10 C放电下放电截止时的温度与实验测试温度相差较小，但在放电过程中存在偏差。同样采用多种误差方式来判断高倍率放电过程中Rint模型的精度，其结果如图11所示。

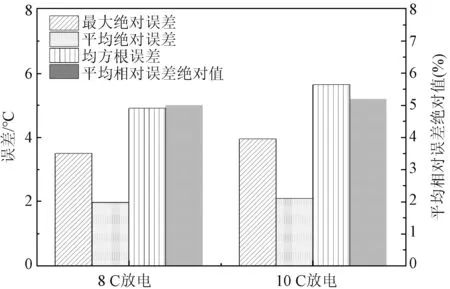
图11 不同高倍率下Rint模型误差对比Fig.11 Comparison of Rint model errors under different high discharge rates

根据图11可知，在8 C、10 C放电时，Rint模型的Max.E、RMSE、MAE、MARE均控制在4 ℃、2 ℃、6 ℃和5%，且两种倍率下误差的差值约为0.5 ℃、0.5 ℃、0.2 ℃和0.2%。表明Rint模型也适用于更高倍率的放电。

5 结论

(1)在功率型锂离子电池的三种常用模型中，温度与电流对电池内阻的影响较大。其中，温度越低，电池的内阻参数越大；但电流特性仅对DP模型中参数产生影响，倍率越大，内阻参数越大。三种模型在不同放电工况以及环境温度下，各项内阻均会随SOC的减小而增大。

(2)通过模型误差对比，当电池采用1 C放电时，可采用DP模型进行热特性分析；当电池采用2 C放电时，Thevenin模型不再适用，可采用DP模型与Rint模型进行研究，但前者在精度上优于后者；当电池采用4 C放电时，可采用Rint模型进行热行为研究，且伴随放电倍率增大，该模型也可适用。