基于分段削峰的用户侧储能容量优化配置启发式方法
高广帅,李新国,曾海燕,李 玮,王主丁
(1.输变电装备与系统安全与新技术国家重点实验室(重庆大学),重庆 400044;2.国网湖北省电力有限公司武汉供电公司,湖北 武汉 430012)
1 引言
近年来,电网中负荷峰谷差不断增加,用电高峰又时常导致电力供需不平衡现象发生,为此电网公司加大输配电设备投入,但又导致电网设备综合利用率降低,影响电力系统经济性[1]。由于储能技术可对功率进行灵活双向快速调节[2],具有应对电力供需不平衡的潜力[3],2021年7月国家发展改革委和能源局联合发布了《关于加快推动新型储能发展的指导意见》,提出到2025年实现新型储能从商业化初期向规模化发展转变,到2030年实现新型储能全面市场化发展。由此可见,在相关政策的扶持下,储能在未来5~10年内将继续保持高速发展的态势。其中,用户侧利用储能系统可通过低储高发[4]以及减少自身基本容量电费进行套利[5],同时还能达到削减峰值负荷和降低峰谷差等作用。
针对用户侧储能配置,文献[6]建立的容量优化规划模型考虑了降低用户基本电费和购电费用所带来的经济收益,并采用粒子群优化算法求解。文献[7]以用户侧储能系统全寿命周期内总的净收益为外层目标函数,以储能系统日调度周期内收益为内层目标函数,采用遗传算法和混合整数线性规划法求解所提出的双层优化配置模型。文献[8]考虑了储能带来的环境效益,针对储能参与负荷削峰填谷建立了详细的成本与收益评估模型并采用遗传算法进行求解。文献[9]采用算法包CPLEX以用户侧储能全寿命周期内净收益最大为目标进行储能配置优化。文献[10]建立了双层规划模型对用户侧混合储能容量配置和储能运行控制策略进行优化并采用粒子群算法进行求解。然而,文献[6-10]均未涉及储能电池循环寿命的优化计算,存在电池寿命不确定导致相应效益计算结果误差较大的问题。为了能够较为准确地计算储能系统的循环寿命,可采用等效全循环次数模型将不同放电深度的放电循环折算为100%放电深度下的等效全循环次数[11,12],具体的程序实现过程需先通过雨流计数法计算电池的放电深度,然后根据电池放电深度与循环寿命的对应关系得到电池的等效循环寿命。此外,对于用户侧储能配置,目前没有针对不同负荷曲线的配额规律研究。在模型求解方面[13],数学优化方法和智能启发式算法在实用上存在这样或那样的问题,比如基础数据获取难于人工干预、算法不成熟、计算耗时和针对不同实例可能存在的算法不稳定等难以推广应用,因此迫切需要实用规划思路和方法的研究,在深入研究问题的细节和机理的基础上抓住主要矛盾,这通常要涉及到传统启发式方法。
本文针对大工业用户,从实用的目的出发,以净年值最大为目标进行储能电池的优化配置,并提出了直观、简洁、快速和稳定的分段削峰启发式方法,同时通过合理的指标设计对不同大工业用户的储能配额规律进行研究,算例表明本文方法能够得到合理的规划方案。
2 储能配置相关基础
作为储能优化配置目标函数中年成本和年收益计算的铺垫,本节包括储能电池成本、储能电池寿命和用户两部制电价三部分内容。
2.1 储能电池成本
储能电池成本由储能一次性固定投资成本以及运行维护成本两部分组成。其中,储能一次性固定投资成本与其自身额定容量和额定充/放电功率相关,且这两者在构成储能投资成本上是相互独立的,该成本可表示为:
Cbinv=CbeEbmax+CbpPbmax
(1)
式中,Ebmax、Pbmax分别为储能电池的额定容量和额定充电、放电功率;Cbe、Cbp分别为储能单位容量和单位充电、放电功率造价。
2.2 储能电池寿命
2.2.1 等效全循环寿命
储能运行过程中存在寿命损耗,通过充放电循环次数体现,可由放电深度估算(放电深度不同,储能可循环次数不同,储能电池的实际使用寿命也不同)。储能电池在实际使用过程中并不是每次都是以100%放电深度进行充放电,须将各次不同深度的放电循环折算为100%放电深度下的等效全循环次数[11,12],然后根据电池100%放电深度与循环次数的对应关系计算出电池的等效循环寿命。
定义储能电池第k次循环周期的放电深度为DODk,则相应的等效寿命折损次数可表示为:
(2)
式中,Ncycle(DOD1)为当放电深度为100%时达到寿命终点所对应的循环次数;Ncycle(DODk)为当放电深度为DODk时的循环次数。
基于式(2),电池在一天工作周期内的总等效寿命折损次数可表示为:
(3)
式中,Ndcyc为储能电池每日的充放电循环周期个数。
则储能电池循环寿命(年)可表示为:
(4)
式中,Nd为储能电池全年有效工作天数。
2.2.2 储能电池的日历寿命
储能电池的日历寿命Tb由电池的浮充寿命Tfloat和基于放电深度的循环寿命Tcycle中的较小值确定,即:
Tb=min{Tfloat,Tcycle}
(5)
浮充寿命Tfloat是固定的服务年限,循环寿命Tcycle则反映了储能电池达到最大循环次数时所对应的工作年限。当实际应用中储能电池的循环次数较少时,计算所得的循环寿命会远远高于浮充寿命,日历寿命即等于浮充寿命。
2.3 大工业用户两部制电价
目前,我国对于大工业用户(变压器总容量在315 kV·A及以上的工业用户)用电实行两部制电价,它将电价分为基本电价和电度电价两部分[7]。其中基本电价按照工业用户的变压器容量或者最大需量(1月中每15 min或30 min平均负荷的最大值)按月收取,不管企业是否用电,都需要缴纳,并与实际用电量无关;电度电价按照实际耗电量收取,并采用分时电价计费(如分为峰时、平时和谷时电价)。月容量电价C′bas和最大需量收费Cbas可分别表示为:
C′bas=csSt
(6)
Cbas=cdPmd
(7)
式中,cs为容量计费单价,元/(kV·A·月);cd为需量计费单价,元/(kW·月);St为变压器容量,kV·A;Pmd为企业月最大需量,kW。
3 储能配置优化模型
用户侧储能配置主要涉及大工业用户电池储能配置的容量和功率,相关收益包括低储高发电价套利收益和最大需量(或容量)减小获得的收益。其中,低储高发电价套利是通过低谷时段低价购电来满足高峰时刻的用电需求,以降低高峰时刻的购电费用;最大需量减小收益即针对大工业用户高峰负荷持续时间短且功率大的特点,利用高峰时段储能放电来削减最大负荷功率,从而降低最大需量费用获得的收益。
针对大工业用户i,储能配置的优化模型可表示为:
(8)
其中
B1,i=Nm,i(cdΔPxf,i)
(9)
(10)
(11)
Cbinv,i=CbeEbmax,i(Tb,i)+CbpPbmax,i
(12)
(13)
(14)
式中,fu,i为在用户i配置储能电池的净年值;Cbinv,i为在用户i配置储能电池的投资(为电池寿命Tb,i或容量的函数);B1,i为用户i储能为最大需量减小带来的年收益;B2,i为用户i储能低储高发电价套利年收益;kz1,i、ky1,i和kh1,i分别为用户i储能投资的折旧系数、运行维护费用系数和回收系数(均为优化变量Tb,i的函数,其中由于折旧一般按平均年限法计算,而运维费用可基于折旧计算,因此折旧费用和运维费用都可按寿命年限直接平摊到每年);SOCi、SOCmin,i和SOCmax,i分别为用户i储能电池运行中的荷电状态、最小荷电状态和最大荷电状态;Ndcyc,i为用户i储能电池典型日充放电循环周期个数;DODi,j为用户i储能电池典型日第j次循环周期的放电深度;Nd,i和Nm,i分别为用户i年运行天数和年运行月数;A/P为资金回收系数;Ebmax,i和Pbmax,i分别为在用户i储能电池的额定容量和额定充/放电功率;ΔPxf,i为用户i配置储能电池后月最大需量减小值;Nh为日采样时刻总数或时间分段总数;ΔPd,m,i和ΔPc,m,i分别为第m个采样时刻的放电功率和充电功率,且ΔPd,m,i·ΔPc,m,i=0;c1、c2和c3分别为对应负荷曲线峰、平和谷时段的电价;Ω1、Ω2和Ω3分别为典型日负荷曲线峰、平和谷的时段数集合;r为基准收益率;η1为预计储能电池净残值率(如0.05);αyz1为储能电池运行维护费用系数按折旧系数提取的比例(如0.6)。
4 模型求解方法
本文从实际规划应用的目的出发,基于简单方法解决复杂问题的思路,提出了简洁直观的分段削峰启发式求解方法,涉及总体思路、储能电池功率和容量的优化配置,以及模型的求解步骤。
4.1 思路和方法
由于大用户负荷受季节性影响较小,而且在规划阶段准确数据难于搜集,通常可做适当的近似计算,即将年平均日负荷曲线作为典型日负荷曲线[9]。
4.1.1 分段削峰法
针对优化模型目标函数中涉及到的负荷曲线峰值削减,本文提出了基于不同削峰率的最大功率分段削减思路和方法进行模型的求解。
负荷曲线最大功率分段削减计算是将最大功率按若干个小的功率分段步长ΔP削减为一系列离散的峰值,在最大功率按固定小步长ΔP逐段减小的过程中,寻找净收益最大的步长个数或削减峰值。尽管这种将连续的峰值动态变化视为多个离散峰值处理的方法会带来一定误差,但如果步长ΔP取得适当且相关算法设计恰当,可以在计算量不大的情况下使规划计算误差得到有效控制。其中,分段计算步长ΔP一般为相应负荷曲线峰谷差的1%左右。
考虑到储能电池的成本结构和收益构成,最大功率的减小方向一般是从最大负荷开始逐渐减小,且在最大功率按固定小步长ΔP逐段减小的过程中,净收益会呈现先增加后减小的趋势,因此可利用这一特点简化计算相关流程。
4.1.2 储能电池功率优化配置
采用分段削峰计算法,则第n阶段削峰后的负荷曲线尖峰功率减小值为nΔP,相应的储能电池放电功率为:
(15)
式中,ηdis为储能电池的放电效率。
针对用户侧或电网侧,储能电池需要在高峰放电低谷充电,且放电电量应等于其充电电量。若当电网最小负荷值增加为Pmin(n)时满足电池充电电量等于放电电量,相应负荷曲线的充电功率为:
(16)
式中,ΔPc,m(n)为第n阶段削峰第m个采样点的储能充电功率;Pm为负荷曲线第m个采样点的功率。
考虑到储能电池在充电过程中存在功率损耗,则储能电池的充电功率为:
(17)
式中,ηc为储能电池的充电效率。
考虑到储能电池的额定功率应同时满足充放电需求,则储能电池的额定功率应为电池充放电功率的最大值,即第n阶段削峰后的储能电池额定功率可表示为:
Pbmax(n)=max{Pdis(n),Pcho(n)}
(18)
4.1.3 储能电池容量优化配置
本文基于电池充放电功率和电量,通过优化放电深度来确定储能电池容量。
(1)最优放电深度的估算
对于某一固定大小的削峰功率,储能电池的充放电功率和电量是确定的,但储能电池的容量可因放电深度的不同而有所改变,从而影响与容量强相关的储能投资及其净收益的大小。在考虑荷电状态限制的情况下,通常放电深度越大储能电池的寿命越短,储能电池的容量越小,而寿命越短年费用趋于越大以及年净收益趋于越小,容量越小则年费用趋于越小以及净收益趋于越大。因此,对于确定的充放电场景(即充放电功率和电量),存在一个最优的放电深度DODopt,使得年净收益最大。
考虑到储能电池实际运行时为避免过充和过放影响储能电池寿命,DODopt(n)应在一定的范围内,即:
DODopt(n)≤SOCmax-SOCmin
(19)
式中,SOCmax和SOCmin分别为储能电池运行荷电状态的上限和下限。
储能电池的最优放电深度可基于式(19)以及储能电池寿命与放电深度的实测关联数据,针对数量有限的放电深度(如0.1,0.2,…,0.8等)采用较为简单的枚举法求得,也可在此基础上结合二分法改善计算精度。考虑到实际规划中难于获得准确的基础数据(如容量电价),放电深度的精确计算意义不大,通常基于不同放电深度的枚举即可获得满足工程计算精度要求的近似计算结果,且由于枚举场景有限计算效率也较高。
(2)储能电池能量波动
对各个采样点的储能电池充放电电量进行累计,可获得对应第n阶段削峰场景下不同采样时刻储能电池相对于初始状态的能量波动,即:
(20)
式中,Eb,m(n)为对应第n阶段削峰场景下储能电池在第m个采样时刻相对于初始状态的能量波动值,即前m个采样点对应的时间段内储能电池累计充放电能量之和,kW·h;Pb,m(n)为储能电池对应第n阶段削峰场景下在第m个采样时刻的功率,充电为正(即ΔPc,m(n)),放电为负(即Pmax-nΔP-Pm,其中Pmax为负荷曲线的最大负荷)。
(3)最优额定容量
针对储能电池在整个典型样本数据周期内的能量波动(该周期内储能电池充放电量基本保持一致),根据储能电池最大和最小能量之差,并考虑储能电池放电深度的优化,可得到储能电池应配置的容量,即对于第n阶段削峰场景,储能电池的额定容量可表示为:
(21)
式中,DODopt(n)为在第n阶段削峰场景下的储能电池最优放电深度。
4.2 模型求解步骤
分别针对各大工业用户,从最大负荷开始分段削峰的计算流程如图1所示,主要涉及以下步骤:
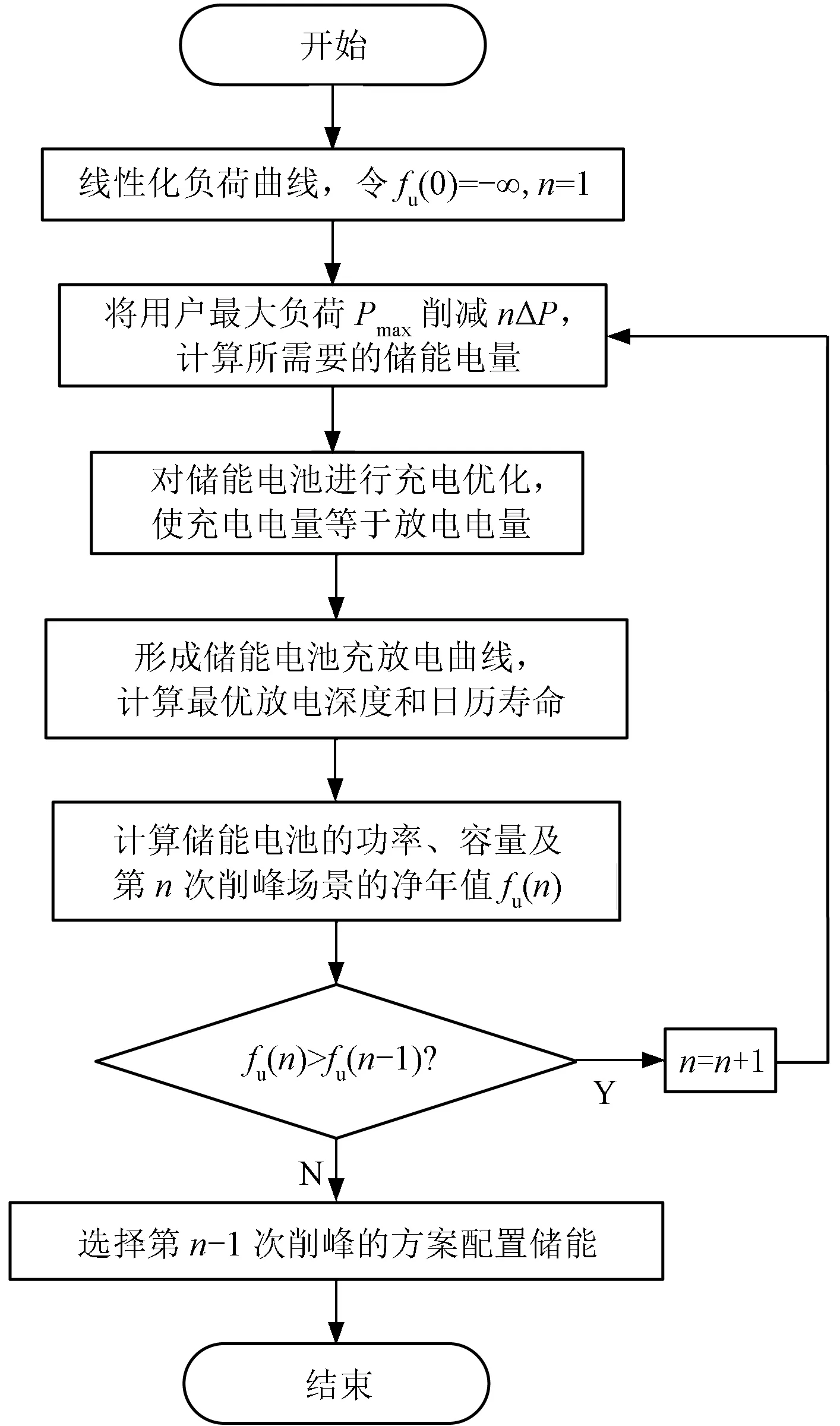
图1 用户侧储能规划优化模型求解流程图Fig.1 Flow chart of optimization model solving for energy storage system planning on user-side
(1)将用户负荷曲线线性化,结果如图2中的实线所示;令年净收益fu(0)=-∞,令削峰阶段数n=1。
(2)以原始负荷削减后仍大于平均负荷为原则,将用户侧的最大负荷Pmax削减到Pmax-nΔP并计算所需的储能电量。以图2中的简单情况(仅削减单峰)为示例,若削减后的最大负荷与负荷曲线交点分别为Ta和Tb,则所需储能电量即为连接Ta和Tb的直线与负荷曲线围成的面积。
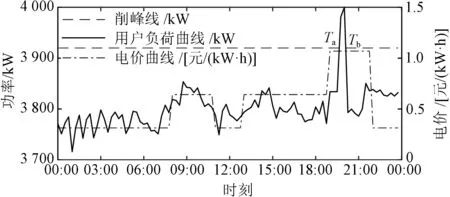
图2 储能规划基本方法示意图Fig.2 Schematic diagram of basic method for energy storage planning
(3)以原始负荷填谷或填平后仍小于Pmax-nΔP以及电池的充电电量等于放电电量为约束,综合考虑净收益受电池容量、充放电次数和深度以及分时电价的影响,对储能电池进行充电优化。
(4)基于步骤(2)和步骤(3)形成的储能电池充放电曲线,运用枚举法和雨流计数法[11]确定储能电池的最优放电深度和日历寿命,进而计算所需储能电池的容量和第n阶段削峰场景下的年净收益fu(n)。
(5)若fu(n)>fu(n-1),令n=n+1,返回步骤(2);否则对应第n-1阶段削峰场景的储能配置方案即为最优方案。
5 储能配额规律研究
储能配额规律研究需要先进行相关影响指标和目标指标的合理选择或设计,然后基于众多样本优化计算结果通过数据挖掘获得目标指标与影响指标间的关系。
5.1 影响指标设计
针对以净收益最大为目标的大工业用户,本文储能配额的影响指标包括反映削峰收益的负荷峰度指标,以及与峰谷电价差套利相关的负荷电价相关度指标。
5.1.1 负荷峰度指标定义
储能电池可通过削减用户的最大负荷获得削峰收益,然而峰谷差之间负荷变化是否陡峭或平缓(或峰值负荷持续的时间长短)影响着所需储能电池容量进而影响成本及收益。本文据此基于采用负荷曲线的不同信息,定义了以下三种类型的负荷峰度指标。
(1)负荷峰度指标1:基于典型日负荷曲线,本文负荷峰度指标1定义为:
(22)
式中,Pave为日负荷曲线的平均负荷功率。
(2)负荷峰度指标2:考虑到典型日负荷曲线中从0到最小负荷(最小负荷一般为大于0的某一数值)之间的部分对储能配置结果没有影响,可仅针对日负荷曲线中最小负荷以上部分定义负荷峰度指标2,其表达式为:
(23)
式中,Pmin为日负荷曲线的最小负荷功率。
(3)负荷峰度指标3:考虑到一般情况下储能系统的最大影响结果为将负荷曲线拉平,可仅针对日负荷曲线中平均负荷功率以上部分定义负荷峰度指标3,其表达式为:
(24)
式中,P′ave为日负荷曲线中仅平均负荷以上部分负荷的平均功率。
5.1.2 电价负相关指标定义
储能电池可通过峰荷放电与低谷充电获得电价差套利收益,即不同时段的电价曲线与负荷曲线的相关性对储能电池的电价差套利收益有较大的影响,本文据此定义了电价相关指标,即:
(25)
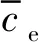
考虑到采用式(25)计算所得结果位于-1~1之间,可通过归一化处理使电价相关指标位于0和1之间,再考虑到储能配额与电价相关指标为正相关,而与负荷峰度指标为负相关,为方便下文基于加权计算的影响指标单一化处理,本文定义了电价负相关指标,即:
(26)
5.2 目标指标设计
为便于使用和找出储能配比与影响指标间的规律,本文定义了以下两种储能配比指标。
(1)峰谷差配比
定义峰谷差配比为储能电池功率与用户典型日负荷曲线的峰谷差之比,即:
(27)
(2)峰平差配比
定义峰平差配比为储能电池功率与峰平差(即典型日负荷曲线峰值负荷与平均负荷之差)的比值,即:
(28)
5.3 配额规律研究思路
首先采用上文优化模型方法获得众多场景(如不同大工业用户典型日负荷曲线样本)储能配置的优化计算结果;然后针对储能配比指标与负荷峰度指标和电价负相关指标的相关性,通过三维曲面拟合识别不同影响指标对储能配比的影响程度(如观察某一指标不变的情况下另一指标变化对配置结果的影响程度),并基于影响程度大的指标权重大于影响程度小的指标权重原则,枚举各影响指标权重的若干组数值(各组指标权重数值之和为1);最后基于各组影响指标权重获得的单一化影响指标,进行目标指标与不同单一化影响指标间的两维曲线拟合,最终选择拟合度较好的指标权重和曲线,从而得到相应的目标指标与各影响指标间的简化优化关系表达式。
6 算例分析
算例涉及到本文方法在不同条件或场景下储能配置和储能配额应用的计算分析。在由Intel(R)Core(TM)i5-5200U CPU @2.20 GHz,4 GB RAM和Windows 10操作系统构成的计算机环境下,针对各应用场景采用Matlab 2018a编程计算用时均在57.44 s左右。
6.1 储能配置计算分析
浙江省某工业用户负荷峰值为61 710 kW,典型日负荷曲线如图3所示。其他相关参数为:基准收益率r=0.08;基本容量电费40元/ (kW·月);工业用户峰谷分时电价见表1;采用的锂离子电池(Li-ion) 放电深度与循环寿命对应关系见表2,相关成本和技术参数见表3。

表3 储能电池相关成本和技术参数Tab.3 Costs and technical parameters of energy storage battery
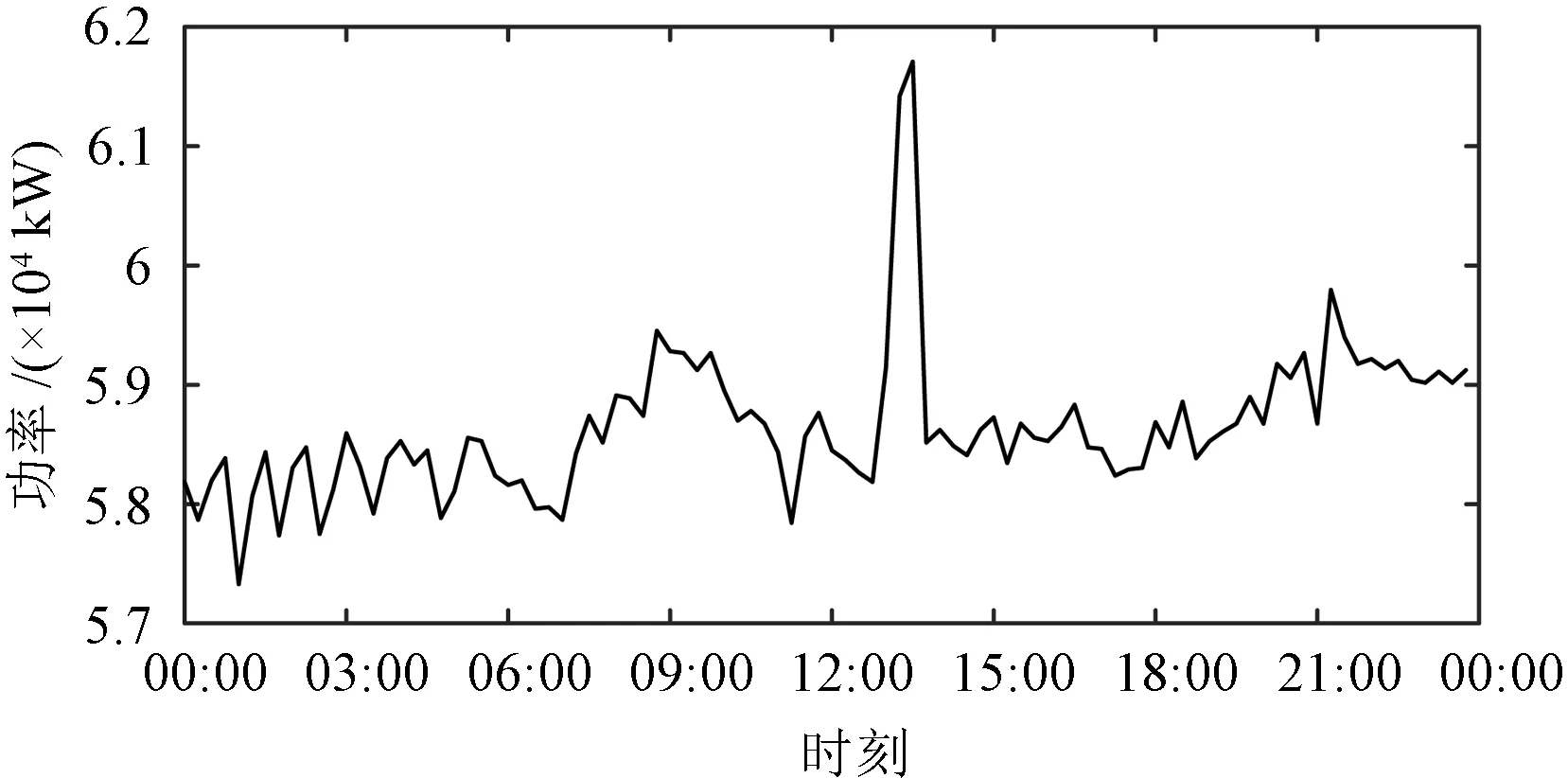
图3 某工业用户负荷曲线Fig.3 Load curve for industry user
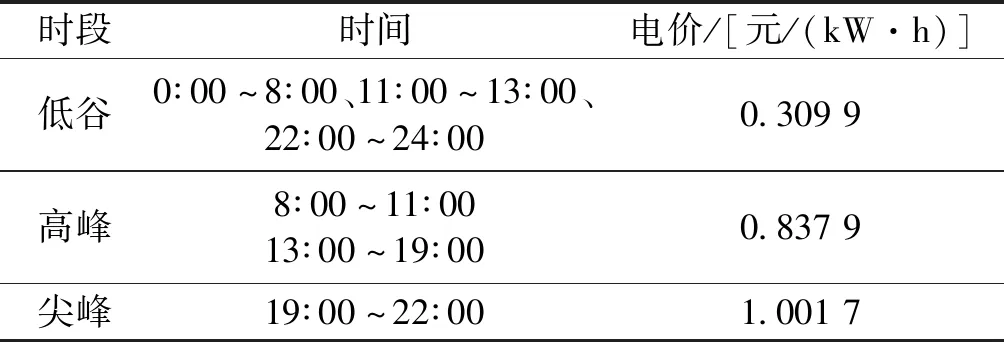
表1 工业用户峰谷分时电价Tab.1 Peak-to-valley time-of-use electricity prices for industrial users
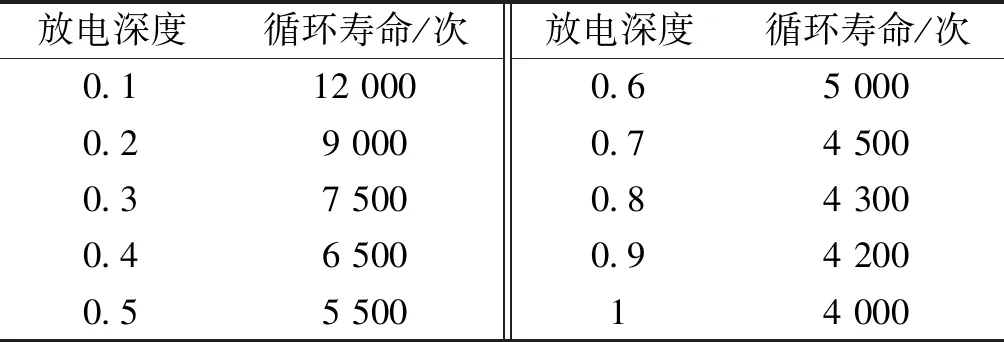
表2 锂离子电池放电深度与循环寿命对应关系Tab.2 One-to-one match between discharge depth and cycle life of Li-ion batteries
采用本文模型和方法,锂离子电池优化配置结果和负荷曲线变化如表4和图4所示。
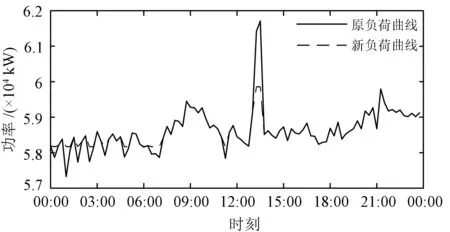
图4 储能削峰前后负荷曲线Fig.4 Load curves before and after peak shaving

表4 锂离子电池优化配置结果(考虑循环寿命)Tab.4 Optimization placement results of Li-ion batteries with cycle life being considered
为了说明电池循寿命对储能配置结果的影响,本文在三种场景下对储能电池进行了优化配置,结果见表5。其中,若不考虑储能电池循环寿命,仅以固定的储能电池15年浮充寿命对储能进行优化配置,计算结果如表5中的方案一所示;若保持方案一中的储能电池功率、容量及最优放电深度不变,利用雨流计数法计算储能电池实际寿命和相应的净年值,结果如表5中的方案二所示;若在保持电池实际寿命为15年不变的情况下进行储能电池的优化配置,结果如表5中的方案三所示。
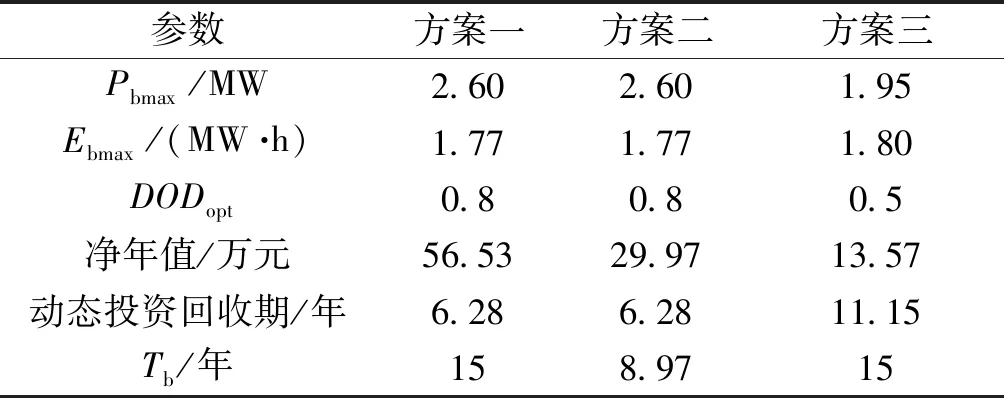
表5 锂离子电池三种对比方案配置结果Tab.5 Placement results of three comparison schemes for Li-ion batteries
由表5可见,方案一中采用的固定15 年电池浮充寿命与方案二中8.97 年的真实寿命相比误差为67.2%,导致相应净年值56.53 万元不符合实际(相比方案二中实际可以获得的净年值29.97 万元误差为88.7%);对比表4可见,表5中方案二配置方案的净年值为29.97 万元,较表4中净年值的优化值36.34 万元减小了17.5%;若要使储能电池达到其浮充寿命,需由原来的放电深度0.8减小至0.5,对比方案二可知,方案三净年值13.57 万元又进一步缩减了54.7%。
6.2 储能配额计算分析
本节储能配额计算分析采用了5.3节储能配额规律研究的思路。
6.2.1 曲面和曲线拟合分析
(1)三维曲面拟合
基于某市34 个大用户的典型日负荷曲线及其储能配置的优化结果,以Δ3(即负荷峰度指标3)为x轴、λcp(即电价负相关指标)为y轴和λ1(即储能峰谷差配比)为z轴进行三维曲面模拟,结果如图5所示。
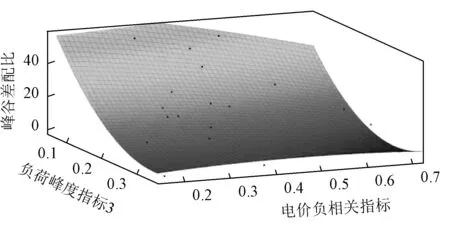
图5 用户侧储能配额三维曲面Fig.5 3D surface of user-side related energy storage quota
由图5可知,在y(电价负相关指标)值保持不变时,z(峰谷差配比)随x(负荷峰度指标3)的增大而减小;同时,在x保持不变时,z随y的增大而减小;且z随x的变化程度远大于z随y变化的程度,即负荷峰度指标相对于电价负相关指标来说对峰谷差配比影响更大。
(2)两维曲线拟合
为将上述三维曲面简化为两维曲线,可将负荷峰度指标与电价负相关指标加权求和来定义一个新的峰谷相关度综合指标,即:
xi=w1Δi+w2λcpi=1,2,3
(29)
基于前文负荷峰度指标和电价负相关指标对峰谷差配比的影响分析,可将式(29)的权重w1和w2分别近似取为0.9和0.1。
基于34个大用户典型日负荷曲线及其储能配置优化结果,分别以xi为横坐标,以λ1和λ2为纵坐标,绘制两维散点图,结果表明采用负荷峰度指标3时规律较为明显,且由于峰谷差配比较为直观,最终选取x3和λ1进行两维加权曲线拟合,结果如图6所示,相应的曲线拟合表达式为:
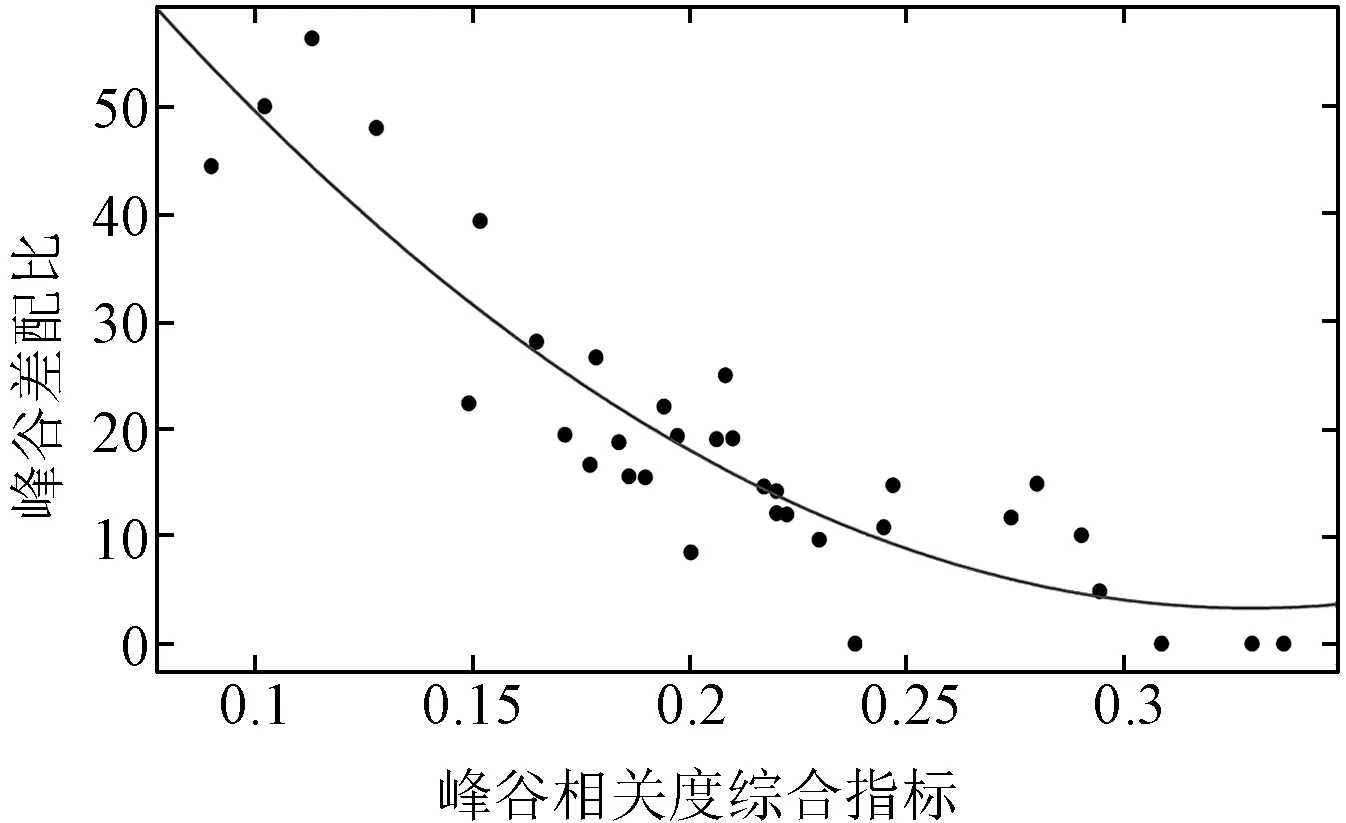
图6 用户侧储能配额两维加权曲线拟合结果Fig.6 Two dimensional weighted curve fitting results for user-side related energy storage quota
(30)
6.2.2 储能配额规律总结
(1)如果负荷曲线不是过于陡峭或平缓,或与负价变化趋势极不相关,本文算例大多数大工业用户的储能峰谷差配比在20%左右。
(2)当峰谷相关度综合指标x3(主要为负荷峰度指标)在10%~15%时,储能峰谷差配比λ1在40%~60%之间;当x3在15%~25%时,配比λ1在10%~30%之间;当x3在25%~40%时,配比λ1在2%~18%之间。
(3)一般情况下,可先基于用户典型日负荷曲线和分时电价数据计算峰谷相关度综合指标,然后采用式(30)计算储能峰谷差配比。
7 结论
本文对配电网用户侧储能电池优化配置的实用模型和方法进行了研究。
(1)模型目标函数为配置储能电池的净收益最大(其中的投资折旧系数、运行维护费用系数和回收系数均为电池寿命优化变量的函数)。
(2)提出了分段削峰启发式方法以对模型进行求解,涉及储能电池最优放电深度和循环寿命的计算。
(3)相比现有的数学优化方法和智能启发式算法,本文方法偏向解析方法,较为直观、简洁、快速和稳定,且便于在实际规划中应用,只要掌握了相应的基本思路,规划人员可借助简单的计算工具甚至仅依靠人工即可完成具体工作。
(4)针对便于在实际储能规划中应用的储能配额制,提出了较为合理的指标设计方案和简化估算公式的推导方法。
(5)算例结果分析表明:
1) 基于大工业用户两部制电价的储能电池配置可获得较大的收益,这是因为两部制电价较为合理地体现了电网或系统的投资,特别是其中的需量计费单价或容量计费单价。针对本文算例,大多数大工业用户的储能峰谷差配比在20%左右(随着储能系统成本的逐渐减小,该配比会有所增大);采用两维曲线拟合得到了峰谷差配比与负荷峰度指标和电价负相关指标间较为一般的关系表达式。
2)将储能电池放电深度优化内嵌于储能电池优化配置中可得出储能电池的实际使用年限,而不考虑放电深度优化的储能规划方案可能使相关计算结果产生较大的误差。

