基于多源特征信息融合的油浸式变压器故障智能诊断模型

李腾飞，郝玉杰，袁 方，孙 锴，马 晶，刘 俊，彭 鑫

(1.国网陕西省电力有限公司超高压公司，陕西 西安 710000；2.西安交通大学电气工程学院，陕西 西安 710049)

1 引言

电力变压器是电力系统能量传输和转换中应用最广泛的核心设备之一，其运行的健康状态密切关系着系统的安全可靠运行[1]。然而变压器在运行过程中，由于绕组变形、主绝缘老化等原因可能会发生故障。近年来，变压器故障引发的事故时有发生，如：2019年特高压泉城站变压器发生爆燃引起火灾及人员伤亡、2019年昭沂直流±800 kV输电工程沂南换流站极II低端Y/Y-C相换流变压器故障着火等。因此，如何有效进行变压器的故障诊断是目前国内外亟待解决的问题。

油浸式变压器在发生故障时，由于变压器油的分解、固体绝缘材料的分解以及一些其他原因[2]，会分解产生一些气体，如：氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)等。基于对上述气体进行成分分析形成的油中溶解气体分析法(Dissolved Gases Analysis，DGA)是常用的变压器故障诊断手段。近年来，基于DGA已形成多种变压器故障诊断方法，如大卫三角法[3]、改良三比值法[4]等。但上述方法都存在信息来源单一、编码边界过于绝对等问题，易出现误诊断的情况。

近年来，人工智能技术快速发展，越来越多学者将神经网络[5-7]、贝叶斯网络[8，9]、支持向量机[10-13]等机器学习算法运用到变压器故障诊断中，并取得了不错的效果。文献[14]利用卡方检验筛选重要特征气体、剔除冗余气体，然后采用不同学习器进行诊断分析，得到最优分类器和最佳特征气体组合。文献[15]利用仿真得到的电气量模拟变压器的故障特征，利用小波分析提取电气量的频域故障特征并进行信息融合，最终采用反向传播(Back Propagation，BP)神经网络进行故障诊断。文献[16]在对比后选择最优的诊断算法进行特征子集选择，利用诊断算法和特征子集训练多个模型，最终在模型间进行选择性融合。文献[17]以归一化后的DGA数据建立了基于XGBoost的故障诊断模型,并采用遗传算法对模型中的多个超参数同时进行优化。文献[18]利用DBSCAN聚类算法建立了变压器故障诊断模型,将DGA数据作为模型的输入得到多种故障的典型聚类簇并进行验证。文献[19]使用托梅克链接移除和自适应样本合成的方法对原始数据进行预处理，随后建立了多种类型的SVM模型进行对比分析。

然而，以上研究都只是利用来源单一的信息对变压器故障进行分类，而变压器又存在较为繁杂的故障机理，仅仅依靠油中溶解气体等单一信息无法在宏观上体现变压器的所有故障[20]。为此，本文提出一种基于多源信息融合技术[21]和卷积神经网络[22]的油浸式变压器故障智能诊断模型。

2 多源信息数据预处理

本文通过西北某省检修公司获取到大量的油浸式变压器故障汇编案例和数据，经整理得到一个包含油色谱分析、高压套管红外检测图谱、放电超声波检测图谱以及特高频局部放电检测图谱的多源异构信息变压器故障数据集。

2.1 高压套管红外检测图谱

红外热像(Infra-Red，IR)技术广泛用于工业检测领域，近年来，已逐渐成为电力设备监测、普查、及时发现隐患、及时抢修、杜绝恶性突发性设备事故的一种手段[23]。

物体的温度变化会引起辐射能量变化，故被测目标的温度可以通过图像信号幅度计算得出，红外测温仪的探测器输出图像信息信号的幅度US表达式为：

(1)

在一定范围内，k1为一常数，由系统增益决定；F(T)由黑体的温度决定。如此，就可以将温度信号转变为电信号，通过电信号的幅值大小判断物体表面的温度高低，进而绘制红外图像。根据颜色的亮暗可以判断变压器套管的温度分布，越亮的图片整体温度越高，变压器发生过热故障的概率也越大。

2.2 放电超声波检测图谱

电力设备内部产生局部放电时，同时产生冲击的振动机械波。放电超声波(Acoustic Emission，AE)检测法通过在设备腔体外壁上安装超声波传感器来测量局部放电信号[24]。

局部放电产生的声强与放电释放的能量成比例，如下所示：

I=μE

(2)

式中，I为声强；E为放电能量；μ为比例系数。

若不考虑空气密度和声速的变化，声强I与声压P有如下关系：

(3)

式中，ρ为空气密度；υ为声速。

根据式(2)、式(3)可知，通过测量超声波声压信号的大小，可以推测出局部放电的强弱，进而能够绘制如图1(b)所示超声波检测图谱。根据波形的幅值大小可以判断变压器内部放电的强弱，幅值越大，则变压器发生高能放电的概率也越大。

2.3 特高频局部放电检测图谱

特高频(Ultra-High Frequency，UHF)法检测技术具有频段高、抗干扰能力强、检测灵敏度高等优点，可用于电力设备局部放电类缺陷的检测、定位和故障类型识别等[24]。

UHF检测法利用特高频传感器对电力设备中局部放电所产生的电磁波信号进行检测，进而推断出局部放电的位点和放电强弱。该方法可有效抑制背景噪声，如空气中电晕产生的电磁波干扰噪声。

如图1(c)所示的局部放电脉冲相位分布(Phase Resolved Partial Discharge，PRPD)图谱，横轴表示局部放电的相位信息，纵轴表示幅值，放电的密度用平面图上点的颜色深浅来表示。通过PRPD可直观地观测出信号的相位变化、幅值变化、放电密度等参数，放电位点越多，则说明变压器发生局部放电的可能性越大。

对于以上四类来自不同信息源的数据，分别进行以下处理：对于DGA数据，其属于数值型数据，可参考行业标准[2]，选择H2、CH4、C2H6、C2H4以及C2H2这5类特征气体的绝对含量，归一化后作为输入信息；另外三类数据均属于图像型数据，对于IR数据，为了避免对样本图片进行复杂且无必要的整体性识别，将RGB+alpha四通道彩色图片转变成单通道的灰度图，并分割出同等大小、只包含高压套管的部分作为IR图像数据的输入信息，如图1(a)所示；对于AE数据，为了避免图片坐标区周围的无用信息产生干扰，本文仅截取包含AE波形图谱的坐标区域，并将其转换成灰度图作为AE波形图谱的输入信息，如图1(b)所示；对于UHF数据，本文舍弃在二维图片上难以分析识别的实时三维图，仅选择显示直观的PRPD平面分析图谱作为输入信息，如图1(c)所示。三类图片的预处理过程如图1所示。

图1 IR、AE、UHF三类图像型数据的预处理示意图Fig.1 Pretreatment diagram of IR,AE and UHF image data

3 基于多源特征信息融合的变压器故障智能诊断模型的建立

3.1 特征提取、融合及网络模型建立

经过上述的数据预处理过程，得到的数据即可作为智能诊断模型的输入信息，下一步就是采用机器学习算法建立智能诊断模型。

对于数值-图像混合型数据，本文搭建包含DNN和CNN的混合型并联网络模型用作特征提取、融合和分类，过程如下：

(1) 首先建立DGA数据部分的DNN模型：

1) 向输入层输入归一化后的DGA数据。

2) 输入层后依次搭建4层神经网络(Neural Network，NN)，其中每层神经元个数分别为8、16、16、8。

3) 输出得到一维向量F1。

(2) 建立图像部分的CNN模型(以IR数据为例)：

1) 向输入层输入规范化后32×32大小的IR图像数据。

2) 卷积层C1采用3×3大小、总数为32个的卷积核分别对输入层的图像进行卷积运算，得到维度为32×30×30的特征图输出到下一次层。

3) 池化层P1大小为 2×2，池化方式为最大池化。经过池化处理后得到32×15×15的特征图输出到下一层。

4) 后续的卷积层C2、池化层P2操作步骤与重复步骤2)和步骤3)。

5) 全连接层F对P2输出的特征图进行展开处理，得到一维的特征向量F2。

(3) 搭建处理AE图像和UHF图像的CNN模型，过程重复步骤(2)。

(4) 将上述过程得到的向量进行融合。向量F2与同样经过CNN处理AE图像和UHF图像数据得到的特征向量F3、F4合并，再与向量F1合并，得到特征融合后的向量V。

(5) 向量V作为输入，向后依次搭建4层NN，每层神经元个数为16、32、32、16。最终输入至分类层，输出诊断结果。

综上所述，本文所提出的多源特征信息融合的变压器智能诊断模型的完整过程如图2所示。

图2 多源特征信息融合的变压器智能诊断模型框架Fig.2 Transformer intelligent diagnosis model framework based on multi-source feature information fusion

3.2 决策诊断和评价指标

变压器故障主要包括过热故障和放电故障两大类，再参考行业标准，本文将故障类型细分为5类，加上无故障(No Fault，NF)的正常状态，一共可以将样本标定为6类，分别见表1。

表1 变压器故障分类标签Tab.1 Transformer fault classification label

本文所述多源信息中的IR图像数据主要体现了变压器的过热故障，其在过热故障类型中可以区分LT与HT；AE、UHF图像数据主要体现了变压器的放电故障，在放电故障类型中，AE图像数据可以区分出LD与HD，而UHF图像数据则重点区分出PD类故障。

针对本文的多分类机器学习问题，由于其样本中6类样本分布并不均匀，其中正常样本和局部放电故障样本数少于其余4类，因此本文采用带改进的交叉熵作为网络训练时的损失函数，同时采用kappa系数作为模型效果的评价指标。

(1) 改进交叉熵损失函数

交叉熵(Cross Entropy，CE)是信息论中一个重要概念，也是神经网络中常用的损失函数，其计算为：

(4)

式中，k为第k类样本；p为真实的类别分布；q为预测的标记分布。

对于本文的不均衡样本集，直接采用式(4)的损失函数会使模型趋于将样本诊断为占比较大的类别，因此精度会大幅降低。为此，本文提出以下带权重的改进交叉熵CEω代替传统的交叉熵作为本文模型训练的损失函数，其表达式为：

(5)

式中，ω(k)为第k类样本的权重。其计算为：

(6)

如此以来，通过给予占比小的样本以更大的权重、占比大的样本以更小的权重，可以有效缓解模型的错分倾向性。

(2)kappa系数

kappa系数常用于一致性检验，也可用作衡量分类精度，其计算如下：

(7)

式中，po为预测正确的样本数除以总样本数，即总分类精度。

假设总类别数为m，每一类的真实样本个数分别为a1,a2,…,am，而每一类的预测样本个数分别为b1,b2,…,bm，总样本个数为n，则有：

(8)

kappa系数能够惩罚模型的“偏向性”，对于评估样本不平衡的数据集有着独特的优势。通常kappa的取值区间为[0,1]，其预测结果相比真实结果的一致性根据取值情况分为表2所示的5类。

表2 kappa系数的一致性检验表Tab.2 Consistency test table of kappa coefficient

4 算例分析

在变压器的故障检测及诊断领域，油中溶解气体检测以及高压套管红外检测已经能够实现在线化，而超声波检测和局部放电检测大多在变压器出现故障后，作为辅助的故障诊断手段。因此，不同的检测方法存在检测周期不同的问题。本文从西北某省检修公司获取大量变压器故障汇编案例和数据，对这些不同时间尺度的检测数据进行如下数据融合处理：①对于样本油色谱检测数据或者红外检测数据缺省的，剔除该样本；②对于样本超声波检测或者局部放电检测数据缺省的，若该样本存在历史数据，则沿用最近一次检测时的结果；否则，采用该样本所属故障类别其余样本的均值代替缺省值。

经过上述的处理，再剔除冗余和异常样本后，经过整理得到1 019个样本，其中各种变压器状态在样本集中的分布见表3。随机选择其中764(75%)个作为训练集，另外255(25%)个样本作为测试。

表3 变压器故障诊断数据集Tab.3 Transformer fault diagnosis data set

4.1 信息融合后模型性能对比

为了验证经过多源特征信息融合后，模型的精度能够得到显著的提升，本文设置三种方案分别进行建模分析，见表4。

表4 多源特征信息融合的变压器故障诊断模型对比方案Tab.4 Comparison scheme of transformer fault diagnosis model based on multi-source feature information fusion

4.1.1 学习曲线和测试精度研究

针对以上三种方案，分别进行建模分析后，训练过程中的学习曲线和最终测试精度如图3和表5所示。

表5 多源特征信息融合的变压器故障诊断模型精度对比Tab.5 Accuracy comparison of transformer fault diagnosis model based on multi-source feature information fusion

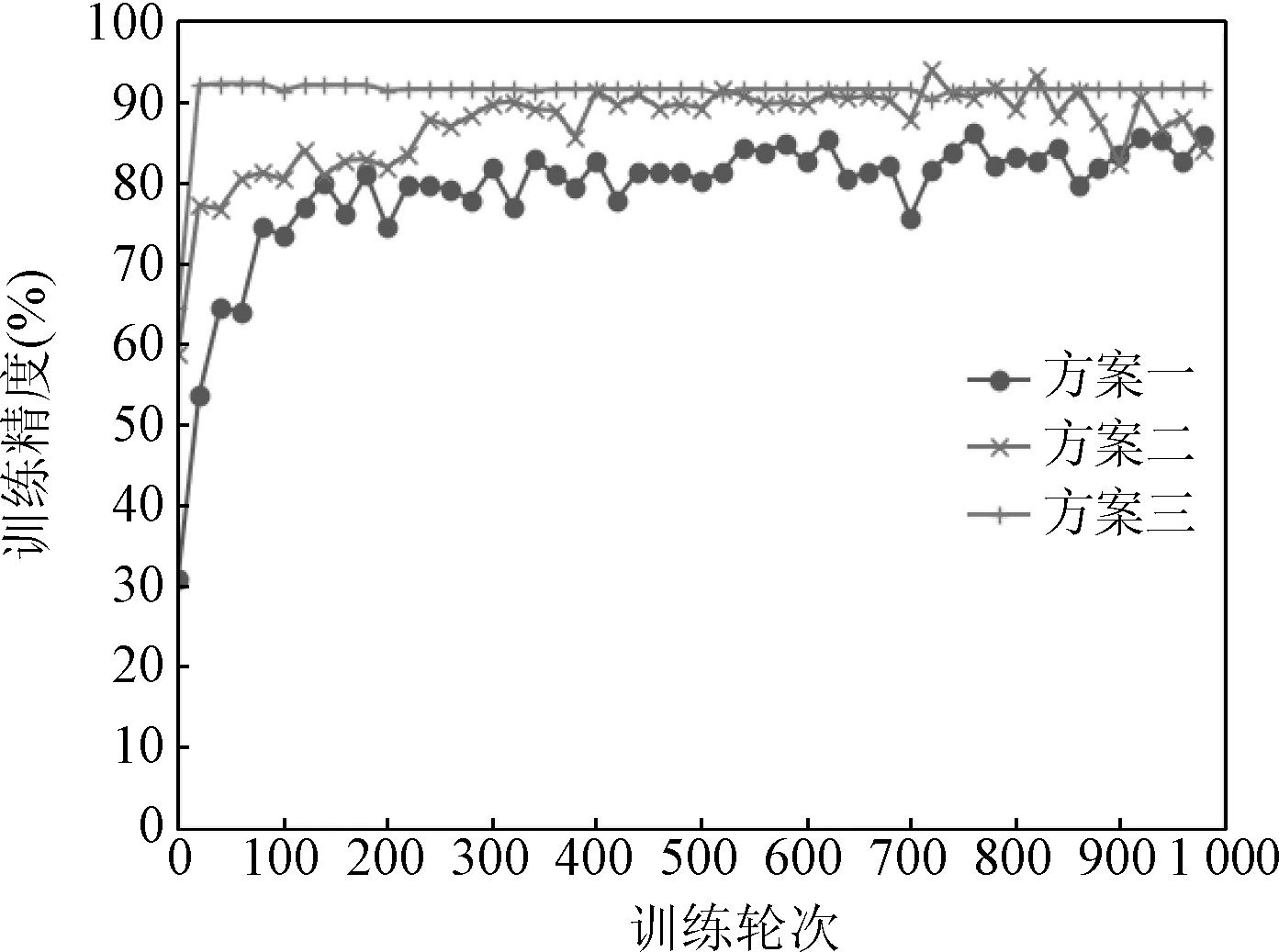
图3 三种方案的训练曲线Fig.3 Training curves of three schemes

从各个模型的训练曲线可见，方案三即本文所提基于多源特征信息融合的变压器故障智能诊断模型收敛速度更快，在前20轮已经能够到达超过90%的训练精度，说明其训练效率最高。此外，方案三最终的测试精度为96.47%，相比于方案一和方案二有着很大的提升。横向对比方案一、方案二、方案三可知，随着输入信息源的增加，模型的诊断效果也逐渐变好，这说明多源特征信息融合可以有效提高变压器故障样本的正确分类。

4.1.2 模型评价与优化

对于多分类问题，混淆矩阵能够清晰反映模型的预测结果。混淆矩阵的每列代表数据的预测类别，每行代表数据的真实类别，位于对角线上的数据为预测正确的样本数。

三种方案预测结果的混淆矩阵如图4所示。图4中矩阵方格中的数字表示当前类别的个数，例如图4(a)第2行第2列的数字“33”表示真实故障为LT、预测结果为LT的样本个数；右侧尺度条颜色深浅表示样本个数的多少，越深个数越多。

图4 三种方案预测结果混淆矩阵Fig.4 Confusion matrix of prediction results of three schemes

由混淆矩阵可知，方案一由于缺少所有图像数据，仅含有DGA数值型数据，每一类别的预测效果都不理想；方案二由于缺乏AE、UHF数据，对三类放电故障，即LD、HD、PD分类效果不佳；而方案三包含本文提出的所有数据信息，每一个类别的预测精度都很高，这再一次验证了多信息源数据融合对模型预测的提升效果。值得注意的是，方案三预测错误的样本主要集中在LT和HT，具体表现为：将4个实际为LT的样本预测为HT，将3个实际为HT的样本预测为LT，并且方案一、方案二也存在类似的问题。这说明CNN对于IR图像的特征提取效果不及AE、UHF图像，至于具体原因是IR图像型数据自身的区分度不够，还是网络结构的问题，还需要进一步研究。

此外，三种方案kappa系数和其所属级别见表6，可知方案三kappa系数远高于方案一和方案二，且其分类结果所属级别为“几乎完全一致”。

表6 三种方案的kappa系数及其一致性检验结果对比Tab.6 Comparison of kappa coefficient and consistency test results of three schemes

4.2 采用改进交叉熵损失函数对模型的影响

考虑到变压器的故障诊断存在数据集样本不均衡的特点，本文提出了带权重的改进交叉熵代替传统的交叉熵作为本文模型训练的损失函数。为了验证其效果，分别采用改进交叉熵和传统交叉熵损失函数搭建模型，并作对比。由于无故障样本数和局部放电故障(Partial Discharge，PD)样本数较少，因此主要分析这两类样本的查准率Prec和查全率Recall，二者可由分类问题混淆矩阵(见表7)计算得到。

表7 二分类问题混淆矩阵Tab.7 Confusion matrix of binary classification problem

(9)

(10)

最终，两个模型的对比结果如图5所示，图5中Accuracy为模型总的预测精度。

图5 采用改进交叉熵损失函数对模型的影响Fig.5 Influence of improved cross entropy loss function on model

由图5可见，采用改进交叉熵作为损失函数后，模型对于NF、PD这两类样本较少的故障类型都有明显的改善作用。同时，整个模型的准确率也有提升，完全符合预期。

4.3 不同学习算法的对比

为了验证本文所提出方法在处理多源特征信息融合数据的应用价值，选择在多分类问题中常用的K近邻(K-Nearest Neighbor，KNN)和随机森林(Random Forest，RF)与本文所提方法进行对比，结果见表8。

表8 不同学习算法的对比Tab.8 Comparison of different learning algorithms

由于这两类算法无法直接处理图像数据，因此对于IR等图像数据，将其展开排列成一维向量并进行归一化，然后与DGA数据合并为总的向量作为输入信息。此外，这两种方法均采用网格搜索法和十折交叉验证进行参数寻优。计算得KNN的最佳近邻个数为19、距离度量d为欧氏距离、权重ω为不均等权重(距离近的比距离远的影响大)；RF的最佳树个数N为120、树的最深深度MD为15、树的最大特征数量MF为11。

最终结果表明这两种算法的识别准确率和kappa系数都低于本文所提出的方法。

5 结论

变压器故障诊断技术是目前国内外亟待解决的问题，现有研究普遍存在信息来源单一、诊断预测精度不高等问题，为此，本文提出一种基于多源信息融合技术和卷积神经网络的变压器故障智能诊断模型。

(1)所提出的基于多源信息融合技术和卷积神经网络的变压器故障智能诊断模型，可针对不同类型的输入数据，分别利用DNN与CNN进行特征提取和数据融合，最后的模型预测准确率达到96.47%，具有很好的识别效果。

(2)为防止由于数据集样本不均衡而造成的模型倾向性，本文提出带权重的改进交叉熵作为模型的损失函数。通过与采用传统交叉熵的模型对比发现，在NF、PD这两类样本数较少的故障类型中，采用改进交叉熵的模型效果提升明显。同时，整个模型的精度也有提升。

(3)本文将所提出方法与KNN、RF两种多分类算法对比，经过参数寻优和交叉验证后发现，本文所提出方法的识别准确率和kappa系数都大幅高于其余两类算法。这说明卷积神经网络在处理图像类数据时表现出了更加优越的性能，再一次验证了该模型的实用性和有效性。