考虑风电不确定性的电力系统惯量评估方法
张 磊,熊致知,叶 婧,程 龙
(1.三峡大学电气与新能源学院,湖北 宜昌 443002;2.国网湖北省电力有限公司十堰供电公司,湖北 十堰 442012)
1 引言
惯量是衡量电力系统抵抗功率不平衡、抑制频率波动能力的重要指标[1],对其准确评估有助于掌握电力系统的频率支撑能力。随着传统电力系统向以新能源为主体的新型电力系统转型升级[2],具有差异化惯量响应特性的新能源电源不断装机投运,使得电力系统惯量呈复杂的非线性时变特征,难以准确量化评估。同时,新能源传输功率与电网频率解耦,致使低惯量系统的频率稳定性恶化[3,4]。为此,开展新型电力系统惯量连续评估研究,实现系统惯量连续监测,对频率失稳风险预警以及保证电网安全稳定有重要意义。
电力系统运行状态数据可通过相量采集单元(Phasor Measurement Unit,PMU)和广域监测系统(Wide Area Measurement System,WAMS)实时获取[5],基于此,国内外学者在扰动事件发生后,利用测量的电力系统时域响应数据对系统惯量进行评估[6,7]。针对评估结果存在偏差的问题,文献[6]将电网划分多个区域分别评估,文献[7]基于频率和电压特性修正摆动方程,从方法层面改善评估效果。在数据方面,文献[8]考虑扰动发生时间和扰动状态数据不准确对惯量评估精度的影响,但无法摆脱对大扰动频率事件的依赖。
然而,大扰动事件不是时有发生,系统遭受小扰动与大扰动下的系统频率幅值波动大、扰动时段固定的特点不同,其数据可靠性难以保障[9]。因此,基于小扰动信息提出马尔科夫-混合高斯模型[10],施加探针扰动信号以闭环辨识电力系统惯量[11],从频率信号中等效估计频率变化率[12]的研究,有效地避免评估偏差。
电网实际运行过程中,不平衡功率和频率扰动始终存在,扰动后的系统惯量评估方法研究为系统惯量连续评估提供思路。文献[13]提取常态化类噪声信息连续估计电网惯量,文献[14]采用功率谱密度分析的电力系统等效惯量评估方法,实现了电网运行时系统惯量监控。上述研究在连续实时惯量评估方面进行了有益尝试,但对新能源电源惯量支撑作用考虑不充分,往往导致评估结果较为保守。此外,新能源出力不确定性加剧了电力不平衡,造成系统惯量水平日内出现强波动性和不确定性[3],因此系统惯量连续实时评估面临不确定场景下的评估精度问题。
针对上述问题,本文提出一种考虑风电不确定性的电力系统惯量连续评估方法。首先,通过分析新型电力系统惯量组成及惯量响应原理,引入惯量中心频率来量化含新能源虚拟惯量的系统惯量;然后,构建考虑新能源不确定性的系统惯量辨识模型,采用鲁棒优化将系统辨识转化为凸优化问题,降低非线性系统惯量辨识的复杂性,进而求解系统惯量;最后,搭建含风电场的四机两区系统的仿真系统,对惯量进行连续实时评估,并验证所提方法的有效性。
2 惯量基本理论
2.1 新型电力系统惯量组成
不同于传统电力系统,以新能源为主体的新型电力系统惯量由同步电机响应的转动惯量、新能源控制策略响应的虚拟惯量共同组成,通过精准评估惯量来表征惯量响应,从而描述系统内部能量转移过程。如图1所示,新型电力系统惯量的组成包括:传统能源的转动惯量HG和新能源的虚拟惯量HR,两者组成系统惯量Hsys,共同响应发电侧和用户侧间不平衡功率ΔP。其中,用户侧负荷在惯量响应阶段的频率调节作用很小,对电网的惯量响应可以忽略不计[1]。以风能作为主要来源的新能源在功率不平衡与频率扰动时的惯量响应特性存在差异,在差异化工况下虚拟惯量策略通过施加控制环节,使风机释放或吸收风机转动部分的旋转动能向电网提供虚拟惯量支撑,用于响应系统频率变化[15],短时间内系统频率不会因为风速突变而跌落。但新能源的虚拟惯量与同步机明确的转动惯量不同,不仅取决于能源资源,还受控制策略的制约,新型电力系统惯量评估难度增大。

图1 新型电力系统惯量组成Fig.1 Inertia composition of new power system
某风电场100%开工况下系统安全稳定运行[12],同一时间段风速、风电场输出功率以及风电场出口频率如图2所示。短时间内风速频繁波动,该波动不是确定性的行为,而是随机变化的,造成风电具有强不确定性。通过虚拟惯量控制策略平滑风速波动性和随机性的影响,使得频率偏移稳定在0.05 Hz范围内,但风电转化过程中风电机组的运行工况变化也会影响不确定性。此外,风电场的有功出力响应频率动态变化过程表明,虚拟惯量一定程度上弥补系统惯量的不足,评估系统惯量应充分考虑新能源电源惯量的支撑作用。与传统电力系统惯量仅由日前同步机机组启停计划决定不同[16],新型电力系统惯量受新能源不确定性影响显著,具有不确定性,因此准确评估系统惯量需计及新能源的不确定性影响。
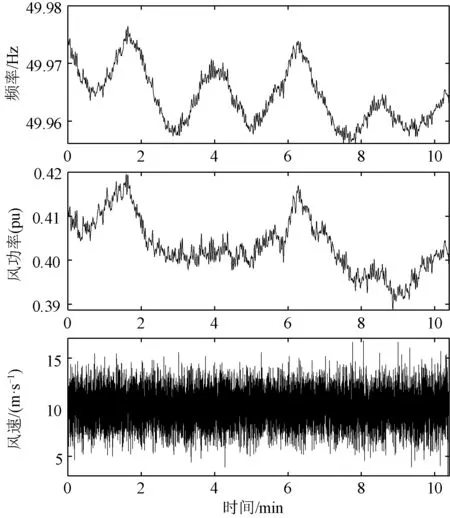
图2 风电场100%开工况测量信号Fig.2 Wind farm 100% operating condition measurement signal
2.2 惯量响应的原理
为应对电力系统频率变化,系统以惯量支撑功率形式响应动作,补充或吸收不平衡功率来稳定系统频率。由于新型电力系统惯量响应特性的差异,造成整个系统频率恢复不同步,因此,本文引入惯量中心(Center Of Inertia,COI)来表示系统的平均频率[17]。定义电网中不同地理分布的各类机组惯量加权的频率均值为惯量中心频率fCOI,计算如下:
(1)
式中,Hi、Sn,i、fi分别为第i台机组的惯量、额定功率、频率;N为机组数量。在表述惯量中心频率时,新能源机组的虚拟惯量支撑作用作为先验知识[18]。
电力系统惯量响应在有功-频率动态变化中体现,惯量中心表征整体电力系统的频率动态特性方程为[19]:
(2)
式中,Dsys为系统阻尼;ΔfCOI为惯量中心频率偏差。由于扰动始终存在,系统功率和惯量中心频率时刻变化,式(2)的动态响应过程中蕴含待辨识的系统惯量特征。
3 基于鲁棒优化系统辨识的惯量评估方法
3.1 系统辨识模型构建
由2.2节分析可知,通过观测系统有功功率、频率数据可以评估出系统惯量参数,惯量评估属于系统参数辨识问题。构建系统辨识模型采用输出误差模型[20](Output Error,OE),表示为:
(3)
式中,u(t)为OE模型的输入,即系统不平衡功率变化率ΔP;y(t)为OE模型的输出,即惯量中心频率偏差ΔfCOI;x(t)为系统内不可观测的真实输出;v(t)为系统噪声;多项式A(q)、B(q)中含有多个待定参数,A(q)=1+a1q-1+…+anAq-nA,B(q)=1+b1q-1+…+bnBq-nB,nA、nB分别为A(q)、B(q)的阶次。
式(3)构建的高阶系统辨识模型中待定参数多,在保证系统辨识模型拟合度的同时减少待定参数,对系统惯量响应时频特性进行分析,其传递函数表达式为:
(4)
系统惯量响应的单位脉冲响应h(t)为:
(5)
单位脉冲响应t=0时表现为扰动下惯量的初始响应,其数值上为2倍系统惯量的倒数。通过式(4)、式(5)的分析将系统惯量响应的高阶辨识模型降阶为一阶传递函数形式,求解模型的初始响应以评估系统惯量。
3.2 基于不确定性的惯量辨识方法
在系统辨识模型确定后,基于最小二乘法理论(Least Squares,LS)将系统辨识模型描述为最小二乘格式:
y(t)=φT(t)θ+v(t)
(6)
式中,θ=[ab],a=[a1…anA]T,b=[b0…bnB]T;φ(t)=[Φ(t)ψ(t)]T,Ф(t)=[-x(t-1) … -x(t-nA)],ψ(t)=[u(t)u(t-1) …u(t-nB)]。
利用PMU实时量测系统有功功率和频率数据,采样长度为m,当t=1,2,…,m时,采样的输入输出数据和对应的系统噪声数据表示为:
将kt写成m×m的矩阵Kt形式,即第一列为kt的下三角Toeplitz矩阵,表示为:
因此,采样得到m个方程式可以将式(6)写为:
yt=Ktθ+vt
(7)
在系统惯量辨识的工程问题中,不确定性输入Kt和输出yt数据间不满足线性关系,采用LS法难以实现无偏估计。非线性数据的不确定性体现在两个方面:①受远动装置性能和数据传输环节的影响,PMU实时数据量测数据存在误差[3];②新能源有功出力具有不确定性,式(1)求取模型的输出ΔfCOI时保留不确定性特征。输入输出数据的不确定性不一定服从概率分布,可表示成K(δ),y(δ)的形式[21]:
(8)
(9)
式中,δKi,δyi分别为输入输出各自的扰动噪声,δy=[δy1…δym]T、δK=[δK1…δKm]T都属于Rm;Ki、ei为扰动方向,ei为m维单位矩阵的第i列,Ki为第一列等于ei的下三角Toeplitz矩阵。
3.3 惯量辨识的鲁棒优化求解
鲁棒优化求解是基于鲁棒最小二乘法(Robust Least Squares,RLS),其原则是:考虑具有式(8)、式(9)形式的输入输出数据[K(δ)y(δ)]的不确定性,使待辨识的系统惯量的结果能实现残差‖K(δ)θ-y(δ)‖2最小,系统辨识模型转化成优化问题来求解:
(10)
式中,ρ为扰动界限;δ为包含δK,δy的扰动噪声,‖δ‖∞≤ρ,即‖δK‖∞≤ρ,‖δy‖∞≤ρ。选取最坏残差作为辨识的准则函数,实现准则函数的最小化获得具有鲁棒性的辨识结果,此时θ为式(10)的RLS解。
(11)
此时,残差的平方是关于不确定数据δ的二次型函数,本文实时量测采样的数据属于连续有界的集合,不难看出该二次型函数的最值存在,进而可以对残差优化求解。
令辅助变量λ≥0,将式(11)的二次型函数运用S-引理优化[22]得到:
(12)
当τ≥0时,式(12)改写为关于λ、τ两变量F(λ,τ)函数的约束形式:
(13)
式中,I为单位矩阵,显然τI≥F的约束中τ≥0。利用矩阵的舒尔补理论将式(13)约束初等变换,辨识问题进一步转化成关于λ、τ函数确定的半定规划问题(Semi Definite Program,SDP)[23]:

(14)
由式(14)可知,在保留辨识模型中多项式时间复杂度的同时,RLS法通过鲁棒对等式近似将辨识问题转化为多项式可解的凸优化问题,采用通用的SDP求解器求解,即可实现不确定条件下系统惯量辨识。
4 系统惯量连续评估方法流程
基于不确定性条件下的系统惯量连续评估流程如图3所示,步骤可以分为数据获取、模型构建、模型求解三部分,具体描述如下:
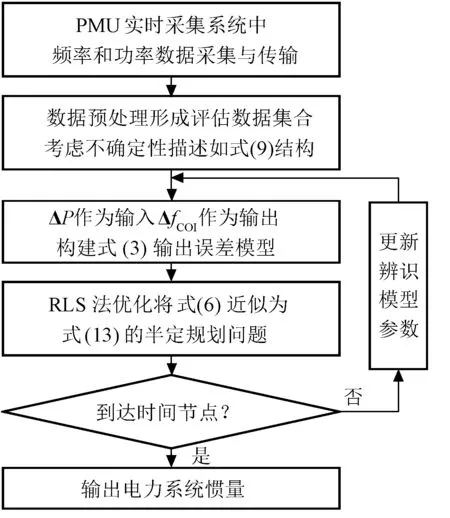
图3 电力系统惯量连续评估流程图Fig.3 Flow chart of continuous evaluation of power system inertia
(1)对PMU实时获得系统内频率与功率数据进行预处理,据式(1)求取的惯量中心频率偏差ΔfCOI,与不平衡功率变化率ΔP形成初始数据样本集合,将其不确定性描述为式(8)、式(9)的形式。
(2)基于式(3)构建的OE模型,通过分析系统有功功率-频率动态过程,解析系统惯量同系统惯量中心频率偏差和有功功率变化率间的耦合关系。
(3)选取最坏残差作为辨识的准则函数,RLS法将原问题转化为确定的式(14)半定规划问题。利用SDP求解器快速求解,在各时间节点更新评估模型参数,完成电力系统惯量连续实时评估。
5 算例分析
5.1 仿真系统
本文所提的方法被应用于改进的典型四机两区仿真系统[24],仿真环境为Matlab/Simulink。如图4所示,装机容量为500 MW的风电场通过母线6接入系统,风电场处风速服从Gumbel分布。为了验证基于鲁棒优化系统辨识的电力系统惯量连续评估方法,双馈异步风力发电机(Double Fed Induction Generator,DFIG)采用虚拟惯量控制策略并网[15],其中DFIG的虚拟惯量时间常数设置为5 s,系统中仿真参数见表1。

图4 改进四机两区域系统模型Fig.4 Improved model of four-machine two-area system

表1 系统各发电机参数Tab.1 System generator parameters
5.2 不同风机工况下系统惯量评估结果的验证
在风电场开机情况分别为10%、40%、70%、100%的工况下,采用本文方法评估系统惯量大小,扰动水平δ取1,得到同一时刻系统惯量结果见表2。其中,风电出力具有不确定性和波动性,表2中计算惯量均含风电场在虚拟惯量控制策略作用下的虚拟惯量。

表2 不同工况下评估系统惯量Tab.2 Evaluate system inertia under different operating conditions
从表2中可以看出,当新能源逐步取代常规机组时,相较不含新能源的典型四机两区系统的系统惯量6.205 s而言[14],系统惯量水平整体下降。对比系统惯量的评估值与设定值可知,本文方法评估惯量误差均在2.50%以内,总体评估结果精度性高。风电场10%开的工况下,评估惯量与设定惯量误差最小,仅为0.36%,风电场100%开工况下误差最大,为2.28%。从风电场开机比例对结果的影响来看,开机比例未过半时评估误差小于0.5%,随着风电场开机比例增加,风电不确定性出力增大,评估的系统惯量误差增长了约2%。由上述不同工况下的评估结果可见,虚拟惯量对系统惯量有一定的支撑作用,高比例风电系统的惯量评估受新能源不确定性影响显著,但采用本文方法较好地处理了辨识数据的不确定性,能精确估计出系统惯量值。
5.3 惯量连续评估结果的对比验证
将本文方法与未考虑不确定性影响的LS法进行对比分析,在风电场100%开工况下,对量测数据采用30 s的移动数据窗,移动步长为15 s,即每15 s更新辨识模型参数以实现系统惯量的连续评估。该风电场处风速连续变化,以1 min内的连续评估为例,每间隔15 s更新系统惯量的评估结果,两种方法对应4个时刻的系统惯量评估结果和误差见表3。
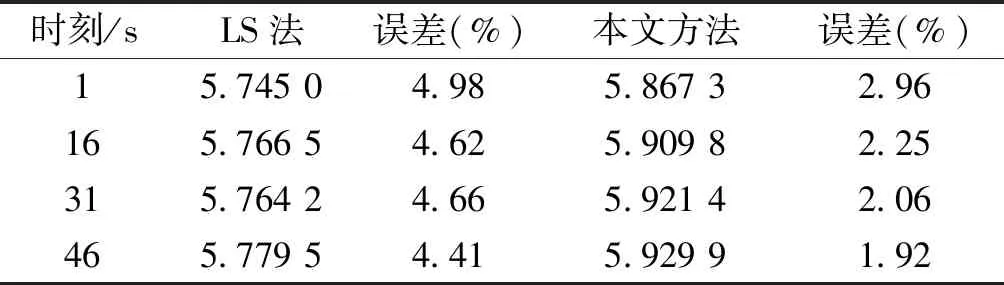
表3 系统惯量评估结果对比Tab.3 Comparison of system inertia evaluation results
由表3结果可知,两种方法均能实现系统惯量的连续评估,在1 min时段内系统惯量没有明显波动。这是由于虚拟惯量策略平滑风速的波动性,短时间内惯量不会因为风速突变而跌落。但采用LS法评估系统惯量时,在1 s、16 s、31 s、46 s时刻节点处误差均高于本文方法,分别为2.02%、2.37%、2.60%、2.49%,本文方法评估结果平均提升了2.37%。评估误差较LS法减小的主要原因在于,本文方法考虑了新能源的不确定性,对外界噪声有很强的抑制作用,具有更强的鲁棒性,可以得到更为精确的系统惯量。
基于系统惯量评估值难以直观反映系统的有功功率-频率动态变化,无法直接提供给系统运行人员操作判断所需信息。为此,进一步验证本文方法的有效性,在惯量连续评估的t=31 s时加设不平衡功率,此时系统有功功率为4.355 pu,系统的不平衡功率ΔP为1.036 pu,功率缺额为23.8%,采用低频减载方案[25]为:频率启动门槛值为49 Hz,启动延时为0.2 s。基于表3中31 s评估惯量结果,此时,系统惯量响应不平衡功率,得到系统频率偏差曲线如图5所示。

图5 系统频率偏差曲线Fig.5 System frequency deviation curve
根据图5和表3数据,当面临严重功率缺额时,基于本文方法评估的系统惯量值,系统频率快速下降但未达到低频减载动作值。而LS法在4.6 s时系统频率偏差已经跌落-1.0 Hz以下,此时,将判断系统触发低频减载。实际上,该时间段内系统频率偏差的变化范围均在±1.0 Hz,系统运行人员无需触发所采用的低频减载方案。本文方法评估系统惯量考虑了风电不确定性影响,用于判断系统不平衡功率缺额下的频率是否会触发低频减载装置动作,判断结果更准确。对比两种评估方法下系统动作看出,对新能源电源惯量支撑作用考虑不充分,将导致系统惯量评估结果较为保守,直接造成系统运行人员采用的安全控制措施不同。
6 结论
本文考虑风电不确定性的电力系统惯量评估方法实现了惯量的连续评估,得到以下结论:
(1)新能源机组通过虚拟惯量控制策略并网具有惯量响应作用,等效的虚拟惯量能为电力系统提供一定的惯量支撑。
(2)所提方法考虑了新能源不确定性,利用不确定性数据信息实现了连续实时系统惯量评估,具有系统惯量在线监控的能力,可以作为频率失稳风险预警的指标,为频率安全控制措施的制定提供新思路。
(3)本文方法对外界噪声有很强的抑制作用,在处理不确定性方面表现出较强的鲁棒性,具有工程适用性。

