基于改进混沌粒子群的PEMFC模型参数辨识
张领先,谢长君,,杨 扬,,刘相万,朱文超
(1.武汉理工大学自动化学院,武汉 430070;2.现代汽车零部件技术湖北省重点实验室(武汉理工大学),武汉 430070)
1 引言
质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell,PEMFC)具有高效率、无污染、使用寿命长、功率密度高、成本低、体积小等优点[1]。基于这些优点,PEMFC应用于航空航天、军事等特殊领域,也在电动汽车和能源系统中具有巨大的应用潜力。由于PEMFC系统是一类极其复杂的非线性强耦合动态系统,建立合适的等效模型并确定模型参数,对于提高整个装置的工作效率和稳定性以及延长其使用寿命具有重要意义[2]。
目前,PEMFC模型[3]可分为机理模型、半经验模型、经验模型和数据驱动模型。PEMFC的机理模型[4]是在一定假设条件下通过基本的物理化学方程构建的。虽然机理模型可以精确地描述PEMFC内部传热传质及电化学反应机理,但其模型复杂,计算成本高。半经验模型[5]是在分析被研究过程机理特性的基础上利用经验公式代替部分复杂机理构建而成,虽然模型有所简化,但是精度仍然较高。经验模型[6]是通过总结每个电池的实验数据,找到相应的数值规律。经验模型比较简单,但存在很多假设,不能适应实际运行情况。数据驱动模型[7]是通过大量实验数据集训练出来的“黑箱”模型,不涉及PEMFC内部机理。虽然精度较高,但是需要大量的数据集用于训练。本文采用了机理模型与经验模型相结合的半经验模型,即综合考虑活化极化损耗、欧姆极化损耗和浓差极化损耗的输出特性模型[5]。
选定模型后,优化模型参数是提高模型精度的关键。近年来,各种元启发式算法被提出用于辨识PEMFC输出特性模型参数。文献[2]提出采用遗传算法(Genetic Algorithm,GA)和新的目标优化函数辨识PEMFC模型参数。文献[5]提出了改进的自适应核糖核酸遗传算法用于PEMFC模型,提高模型辨识精度。文献[8]提出了混合遗传算法(Hybrid Genetic Algorithm,HGA),使用单纯形搜索以提高局部搜索能力。此外,文献[9]使用的差分进化算法(Differential Evolution,DE)和文献[10,11]使用的粒子群优化(Particle Swarm Optimization,PSO)相关改进算法也进一步提高了PEMFC输出特性模型参数辨识的精度。
针对PEMFC输出特性模型参数辨识相关问题,PSO算法有其搜索速度快和效率高的优点。M.Sedighizadeh等人使用改进的PSO算法[12]基于电堆数据进行参数辨识。Q.Li等人提出了一种自适应PSO算法[10](Effective Informed Adaptive PSO,EIA-PSO)平衡局部搜索和全局搜索,提高全局收敛能力。H.Abdi等人提出了一种带收缩系数的PSO算法[13],提高收敛速度。M.Farhangian等人提出Tribe-PSO算法[14]应用于模型参数辨识问题。
基于以上研究,本文结合电堆内部电化学和热力学原理建立PEMFC输出特性半经验模型。结合混沌序列特性,提出一种具有动态惯性权重的混沌粒子群优化(Chaotic Particle Swarm Optimization ,CPSO)算法。基于标准测试函数验证CPSO算法的寻优性能,然后对两种参数不同的电堆进行输出特性模型参数辨识,结果表明,相比其他算法,CPSO算法辨识PEMFC输出特性模型的精度更高。
2 PEMFC输出特性模型
2.1 PEMFC工作原理
PEMFC的基本工作原理如图1所示:①在PEMFC阳极,H2进入阳极流道板,通过阳极扩散层到达阳极催化层,在催化剂作用下分解为氢质子和电子;②氢质子通过质子交换膜到达阴极,电子通过外电路到达阴极;③在PEMFC阴极,O2进入阴极流道板,通过阴极扩散层到达阴极催化层,在催化剂作用下,与氢质子和电子结合生成水并释放能量。外电路中电子的单向运动形成持续的直流电给负载供能。该过程的反应式如式(1)、式(2)所示:
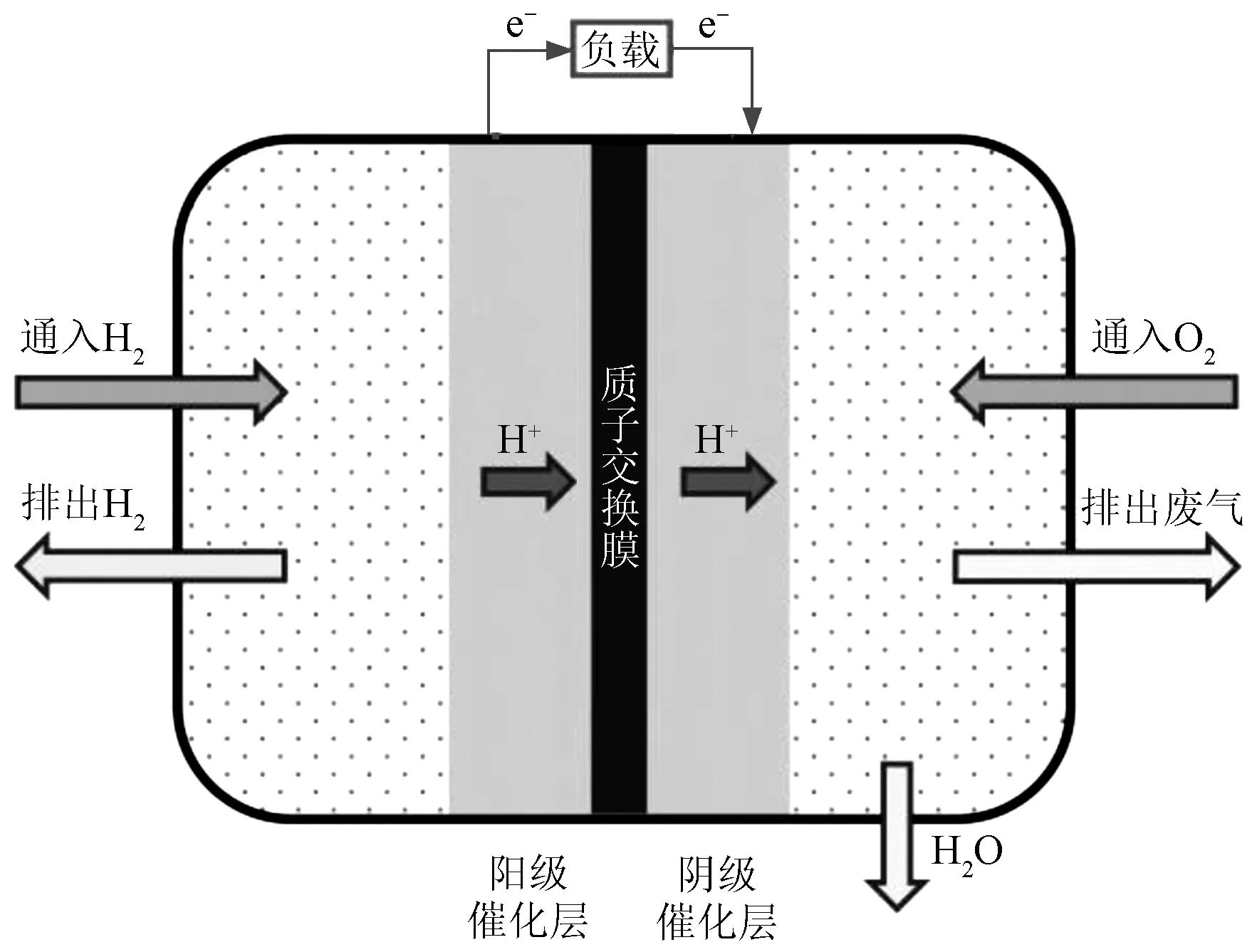
图1 PEMFC工作原理Fig.1 Working principle of PEMFC
H2→2H++2e-
(1)
4H++4e-+O2→2H2O
(2)
2.2 PEMFC半经验模型
本文构建PEMFC半经验模型,即对PEMFC内部气体、质子、水分布和热量分布进行建模,利用能量守恒方程、传质传热方程和电化学反应方程描述相关参数对PEMFC输出特性的影响。当PEMFC接入负载进行供能时,氢燃料电池的输出电压Vcell如下[15,16]:
Vcell=ENernst-Vcon-Vohm-Vact
(3)
式中,ENernst为热力学电动势;Vcon为浓差极化过电压;Vohm为欧姆极化过电压;Vact为活化极化过电压。ENernst由式(4)计算:
(4)
式中,T为PEMFC电堆运行的温度,单位为 K;PO2和PH2分别为O2和H2的分压,单位为 bar,分别由式(5)、式(6)计算:
(5)
(6)
式中,Pa和Pc分别为阳极和阴极的入口压力,单位为 bar;RHa和RHc分别为阳极和阴极中水蒸气的相对湿度;i为电堆的输出电流,单位为A;A为质子交换膜的有效活化面积,单位为 cm2;PH2O为水蒸气的饱和压力,由式(7)计算:
(7)
(8)
式中,b与电池状态有关;J为电池的电流密度;Jmax为电池允许的最大电流密度;b、ξ1、ξ2、ξ3为输出特性模型中需要辨识的参数。欧姆极化过电压Vohm由式(9)计算:
Vohm=i(RM+RC)
(9)
式中,RC和RM分别为电子转移电阻和质子交换膜等效电阻,RC为输出特性模型中需要辨识的参数,RM由式(10)计算:
(10)
式中,L为质子交换膜的厚度,单位为 cm;ρΜ为质子需要克服的阻抗,单位为 Ω·cm,ρΜ由如下经验公式计算:
(11)
式中,λ为质子交换膜的含水量,是输出特性模型中需要辨识的参数。活化极化过电压Vact由式(12)进行计算:
Vact=-(ξ4+ε2T+ξ6TlnCO2+ξ7Tlni)
(12)
ε2=0.002 86+0.000 2lnA+ξ5lnCH2
(13)
式中,CO2为氧气浓度质量分数;CH2为氢气浓度质量分数;ξ4、ξ5、ξ6、ξ7为PEMFC输出特性模型中需要辨识的参数。根据亨利定律有:
(14)
(15)
2.3 电堆模型输出电压
为了满足输出功率和输出电压要求,通常将多个燃料电池单体串联组成电堆。由式(3)可得单个PEMFC输出特性模型的输出电压,假设电池模型的电化学特性一致,则电堆输出电压可以表示为:
Vstack=NVcell
(16)
式中,N为组成PEMFC电堆的电池数量;Vstack为电堆输出电压。
3 改进的混沌粒子群优化算法
3.1 混沌初始化种群
CPSO算法利用混沌映射来改善PSO算法易陷入局部最优解这一问题。PSO算法的迭代是所有粒子持续寻找种群最佳值的过程。优化迭代过程中单个粒子速度和位置的更新公式如式(17)、式(18):
Vt+1=WVt+C1(Xpbest-Xt)+C2(Xgbest-Xt)
(17)
Xt+1=Xt+Vt+1
(18)
式中,Xt和Vt分别为粒子迭代前的位置和速度;Xt+1和Vt+1分别为粒子迭代后的位置和速度;Xpbest为粒子个体历史最佳位置;Xgbest为种群历史最佳位置;W为粒子速度更新的惯性权重;C1为个体学习因子;C2为群体学习因子。
CPSO算法是将PSO算法和混沌搜索策略结合形成的优化算法。本文采用Skew Tent映射产生混沌序列来进行种群初始化,Skew Tent映射的遍历具有均匀性、随机性,从而可以维持种群的多样性,同时提高全局搜索能力。其数学模型为[17]:
(19)
式中,当α∈(0,1)且yt∈(0,1)时系统处于混沌状态。计算数学模型得到混沌序列yt+1∈(0,1),再与参数范围融合,得到混沌化后的初始种群位置。
3.2 混沌扰动
为了改善PSO算法容易陷入局部最优解的问题,对粒子个体施加混沌扰动[18],使粒子跳出当前的局部最优解。详细过程如下:随机产生一个d维分量u0= (u01,u02,…,u0d),d为辨识参数的维度。根据Logistic映射关系:
Zi+1=μZi(1-Zi)i=0,1,2,…;μ∈(2,4]
(20)
式中,Zi为映射函数;μ为控制参数,当μ=4,0≤Z0≤1,上述系统完全处于混沌状态。根据式(20)产生d维分量u1=(u11,u12,…,u1d),u1j=4u0j(1-u0j),j=1,2,3,…,d,将u1的各个分量载波到混沌扰动范围[-β,β]内,扰动增量ΔX=(ΔX1,ΔX2,…,ΔXd)为:
ΔXj=-β+2βu1j
(21)
施加混沌扰动增量后新增位置更新公式为X′t+1=Xt+Vt+1+ΔX,计算其对应的适应度函数值f′,同时计算Xt+1=Xt+Vt+1对应的适应度函数值f。如果f′ 在PSO相关算法中,惯性权重W对收敛速度和收敛性有很重要的影响。基于文献[19]提出的惯性权重更新公式修改,修改后的更新公式为: (22) 式中,iter为当前的迭代次数;ger为算法总迭代次数;Wmax和Wmin分别为惯性权重的最大值和最小值;σ为惯性权重系数,用来控制W与贝塔融合后的偏移程度,提高算法的全局收敛能力;B(b1、b2)为贝塔函数公式,能够提高算法在迭代过程中的随机性,以及加快算法后期的收敛速度。贝塔函数公式为: (23) 式中,当b1和b2取不同的值时,其分布情况不同。根据文献[19],b1=0.1、b2=0.9效果较好。 CPSO算法步骤如下所示: Step1:设置种群规模g,最大迭代次数ger,群体学习因子C2和个体学习因子C1等参数。 Step2:产生基于Skew Tent映射的混沌序列,与参数上下限融合,得到混沌初始化种群,同时定义粒子扰动增量ΔX。 Step3:计算每个粒子对应的适应度函数,更新粒子的个体历史最优值和群体最优值。 Step4:更新粒子的速度并做超界处理。 Step5:更新粒子的速度,施加混沌扰动增量,计算f=F(Xt+1),f′=F(X′t+1),如果f′ Step6:更新粒子的位置,并做超界处理。 Step7:判断当前的迭代次数是否达到最大迭代次数,满足则退出算法,不满足则重新回到Step3。 使用6个标准测试函数对CPSO算法搜索性能进行测试,前4个测试函数为单峰函数,记为f1~f4。而后2个测试函数为多峰函数,记为f5、f6。f1~f6的表达式、理论最优值和输入参数单个维度的数值范围见表1。函数表达式中的D为输入参数的维度,xi代表输入参数的第i维。为了对比CPSO算法的搜索性能,基于6个标准测试函数对GA[2]、PSO[20]、受约束粒子群优化[11](Bound-PSO,B-PSO)算法、具有收缩系数χ的粒子群优化(PSO with constriction coefficientχ,PSO-χ)算法[13]、引力粒子群优化算法[21](Gravitational Search Algorithm PSO,GSAPSO)和DE[9]6种启发式算法也分别进行10维和30维输入参数的性能测试,CPSO算法和其他6种启发式算法的相关参数见表2。 表1 标准测试函数[5]Tab.1 Standarad test function[5] 表2 算法参数设置Tab.2 Algorithm parameter settings 表3 输入参数分别为10维和30维的性能测试结果Tab.3 Performance test results with input parameters of 10 and 30 dimensions,respectively 从表3可以看出,在达到迭代次数时通过比较最终的收敛值来确定收敛精度,在满足绝对误差时通过比较迭代次数来确定收敛精度。对于单峰函数f1~f4,不同的算法有不同的收敛精度表现。但是在输入参数分别为10维和30维的情况下,CPSO算法相对PSO算法有绝对优势,但是相对其他的PSO改进算法则优势较小。对于多峰函数f5、f6,CPSO算法相对其他算法的优势则没有单峰函数大,但是CPSO算法仍然更适合在局部最优解比较多的情况下找到全局最优解。 这7种算法10维输入参数性能测试的收敛趋势如图2所示,横坐标为迭代次数,纵坐标为适应度函数值。从图2的6幅局部放大子图(圆圈圈住的部分为放大区域)可以看出,CPSO算法的迭代起点比其他算法都更低,说明混沌序列初始化有助于降低初始迭代点。此外,分别从图2(a)~图2(d)和图2(e)、图2(f)可以看出,对于单峰函数f1~f4和多峰函数f5、f6,相比GA[2]、PSO[20]、GSAPSO[21]、DE[9]算法,CPSO算法在收敛速度和收敛精度上均有绝对的优势,而CPSO相对B-PSO[11]和PSO- χ[13]则有相对较小的收敛速度和收敛精度优势,这与表3得出的结论是一致的。 图2 f1 ~f6收敛过程Fig.2 Convergence process of f1 ~f6 结合表3和图2的性能测试结果,对于单峰函数f1~f4和多峰函数f5、f6,虽然7种算法在有限迭代次数内都未取得最优解,但总体上CPSO算法相对其他算法有更快的收敛速度和更高的收敛精度。 采用CPSO算法对PEMFC模型参数进行辨识。其中ξ1、ξ2、ξ3、ξ4、ξ5、ξ6、ξ7、λ、RC、b是PEMFC输出特性模型中需要辨识的参数,根据参考文献[5],在两种条件下这10个参数的范围见表4。CPSO算法优化目标函数值越小则算法优化效果越好,由式(24)进行计算: 表4 模型参数的范围[5]Tab.4 Range of model parameters[5] (24) 式中,M为数据点的个数;Vcell为电堆实际输出电压;Vm为建立的PEMFC输出特性模型电压。优化适应度函数Fobj的目的是使模型输出电压与电堆输出电压更为接近。 为了充分验证CPSO算法的辨识性能,采用两种参数不同电堆的数据进行输出特性模型参数辨识,以下简称电堆1[2]和电堆2[6]。 电堆1共包含四组数据,其中阳极入口压力Pa分别为3 bar、1 bar、1.5 bar、2.5 bar,阴极入口压力Pc分别为5 bar、1 bar、1.5 bar、3 bar。前两组数据用于辨识输出特性模型参数,后两组数据用于验证辨识出参数的精度。PEMFC输出特性模型的部分参数设置见表5,表5中Imax为极限电流密度;P为电堆输出功率。 表5 电堆1的参数[2]Tab.5 Parameters of stack 1[2] 为了方便比较辨识结果,在表6中给出了条件1下6种算法的辨识参数、适应度值Fobj、均方根误差(Root Mean Square Error,RMSE)以及平均相对误差(Average Relative Error,ARE),这6种算法即B-PSO[11]、PSO-χ[13]、带有爆炸算子的布谷鸟搜索算法(Cuckoo Search with Explosion Operator,CS-EO)[22]、JAYA-NM[23]、DE[9]和CPSO算法。在表7中给出了条件2下6种算法的辨识参数、均方根误差和平均相对误差。从表6和表7的Fobj对比结果可看出,CPSO算法相比其他算法有一定的精度优势。 表6 电堆1参数辨识结果(条件1)Tab.6 Parameter identification results of stack 1 (condition 1) 表7 电堆1参数辨识结果(条件2)Tab.7 Parameter identification results of stack 1 (condition 2) 基于电堆1前两组电压数据得到辨识参数(条件2)输入模型的模型输出电压,与电堆1前两组实际电压数据对比,如图3所示,且拟合误差在0 V处小幅度波动。图3中,“3bar、5bar”分别为阳极入口压力与阴极入口压力,其余类似。 图3 电堆1训练结果Fig.3 Training results of stack 1 为了验证参数的有效性,将参数输入模型与电堆1后两组实际电压数据对比,如图4所示,且拟合误差在0 V处上下小幅度波动,验证了CPSO算法辨识结果的稳定性。注意到不同数据点的误差幅值不同,这是因为算法的优化目标是使总体误差最小。 图4 电堆1验证结果Fig.4 Validation results of stack 1 结合表6、表7、图3和图4,参数辨识的结果证明了 CPSO算法在PEMFC输出特性模型参数辨识方面的优越性。 电堆2数据来源于Avista Laboratories(爱维斯塔实验室),参数见表8。此实验数据被称为SR12 数据,共 37 组[6]。基于电堆2的极化电压数据,在两种条件下分别使用CPSO、PSO[20]、B-PSO[11]、PSO-χ[13]、GSAPSO[21]和DE[9]进行参数辨识,Fobj、RMSE、ARE和计算时间见表9和表10。 表8 电堆2的参数[6]Tab.8 Parameters of stack 2[6] 表9 电堆2辨识结果(条件1)Tab.9 Identification results of stack 2 (condition 1) 表10 电堆2辨识结果(条件2)Tab.10 Identification results of stack 2 (condition 2) 结果表明,各个算法ARE的大小对比与其性能测试中收敛精度的对比是吻合的。相比其他算法,CPSO算法的拟合误差提升比较小,这是因为电堆2拟合误差集中在电流密度较小的阶段,此时活化极化过电压占主导地位。虽然活化极化过电压计算公式中有4个辨识参数,但是根据表4可知,这4个参数的变化范围均较小,所以最终的误差提升较小。 计算时间这一结果表明CPSO算法相对GA、PSO及其相关的改进算法在精度上有所提升,但其运算量相比GA最高提高了2.5倍左右,这主要是因为CPSO算法每一次迭代,施加混沌扰动模块都会导致增加两次适应度函数的计算。但是CPSO算法运算量与其他算法相比仍然是同一数量级。总体上CPSO算法辨识的Fobj、RMSE和ARE均为最小,CPSO算法相比PSO算法精度提升比较大,但是计算效率受到影响。 将CPSO算法辨识的参数(条件2)输入到PEMFC输出特性模型中计算得到输出电压,在图5中绘制出输出特性模型电压和电堆2实际电压对比,结果表明拟合效果良好。图5中箱线图的箱体代表标准误差,箱线的上下限表示5%和95%的误差分布,箱体内部横线表示中位数。结果表明,CPSO算法的拟合误差总体上分布在更小的区间内,标准误差均匀分布在零刻度线的两侧,且其中位数最小。结合表9、表10中的Fobj、RMSE、ARE以及图5的电压对比结果,再次验证了CPSO算法进行PEMFC输出特性模型参数辨识的优越性。 图5 电堆2参数辨识结果Fig.5 Parameter identification results of stack 2 为比较不同PEMFC模型在不同工况下的性能,采用IEEE 2014 Data Challenge[24]的两种工况数据,基于CPSO算法对3种PEMFC模型进行参数辨识。静态工况记为FC1,其电流恒为70 A。动态工况记为FC2,其电流为70 A的恒流叠加上频率为5 kHz、幅值为7 A的三角波电流。电堆的参数见表11。 表11 IEEE 2014 Data电堆的参数[24]Tab.11 Parameters of IEEE 2014 Data stack[24] 本文使用的燃料电池模型记为模型1,模型2来源于参考文献[5],与模型1的区别为活化极化过电压模型和浓差极化过电压模型,具体为: Vact=ξ4+ξ5T+ξ6TlnCO2+ξ7Tlni (25) (26) 式中,模型2中需要辨识的参数为ξ4、ξ5、ξ6、ξ7、b。模型3[25]与模型2的区别为活化极化过电压模型,其表达式为: Vact=V0+Va(1-e-c0i) (27) 式中,V0为初始电压;Va为过程电压;c0为模型中需要辨识的参数。在静态工况FC1和动态工况FC2下,3种模型在条件1和条件2下训练过程中辨识的误差见表12。为了进一步验证辨识出参数的精度,分别在条件1和条件2两种参数范围下将辨识出的参数分别输入到3种模型中,得到3种模型的输出电压与实际电压数据的对比如图6和图7所示。图6和图7中左侧坐标系为FC1工况下的结果对比,右侧坐标系为FC2工况下的结果对比。 表12 两种工况下3种模型的辨识误差Tab.12 Identification errors of three models under two working conditions 图6 条件1下的电压对比Fig.6 Voltage comparison under condition 1 图7 条件2下的电压对比Fig.7 Voltage comparison under condition 2 结合表12以及图6、图7中可以看出,从不同的参数范围来看,在条件1下,基于FC1和FC2工况进行参数辨识,两种工况下3种模型的误差均有显著的差别。这说明不同的模型对辨识精度有很大的影响。在条件2下,FC1和FC2工况中模型1和模型2的辨识精度较高且接近,模型3拟合误差较大,说明参数范围对参数辨识的精度也有显著的影响。两种条件下模型3的精度始终最低,这是因为其辨识参数数量较少的缘故。 从表12训练过程中的辨识误差可以看出,对于模型1,静态工况FC1下的辨识误差比动态工况FC2更高。对于模型2和模型3,静态工况FC1下的辨识误差比动态工况FC2更低。从图6和图7也可以看出,对于模型1,FC2工况下的电压拟合效果更好。对于模型2和模型3,则是FC1工况下的拟合效果更好。结果说明,模型1对动态工况FC2的适应性更好,而模型2和模型3对静态工况FC1的适应性更好。 本文基于热力学和电化学原理建立PEMFC电堆输出特性模型,提出改进的混沌粒子群优化算法辨识输出特性模型的参数。使用GA、PSO、B-PSO、PSO-χ、GSAPSO、DE及CPSO算法进行性能测试,在测试维度为10维和30维时,CPSO算法均有更高的收敛精度和更快的收敛速度。对于电堆1,CPSO算法在条件1和条件2下的平均相对误差最小,分别为5.016%和2.339%。对于电堆2,CPSO算法在条件1和条件2下的平均相对误差最小,分别为4.901%和1.170%。与其他5种算法相比,CPSO算法辨识后的模型输出误差最小,CPSO算法辨识PEMFC输出特性模型精度较高。最后简单验证了不同工况和不同模型对PEMFC模型参数辨识精度的影响,而基于动态工况进行参数辨识是下一步的研究内容。3.3 动态惯性权重
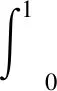
4 CPSO算法性能测试
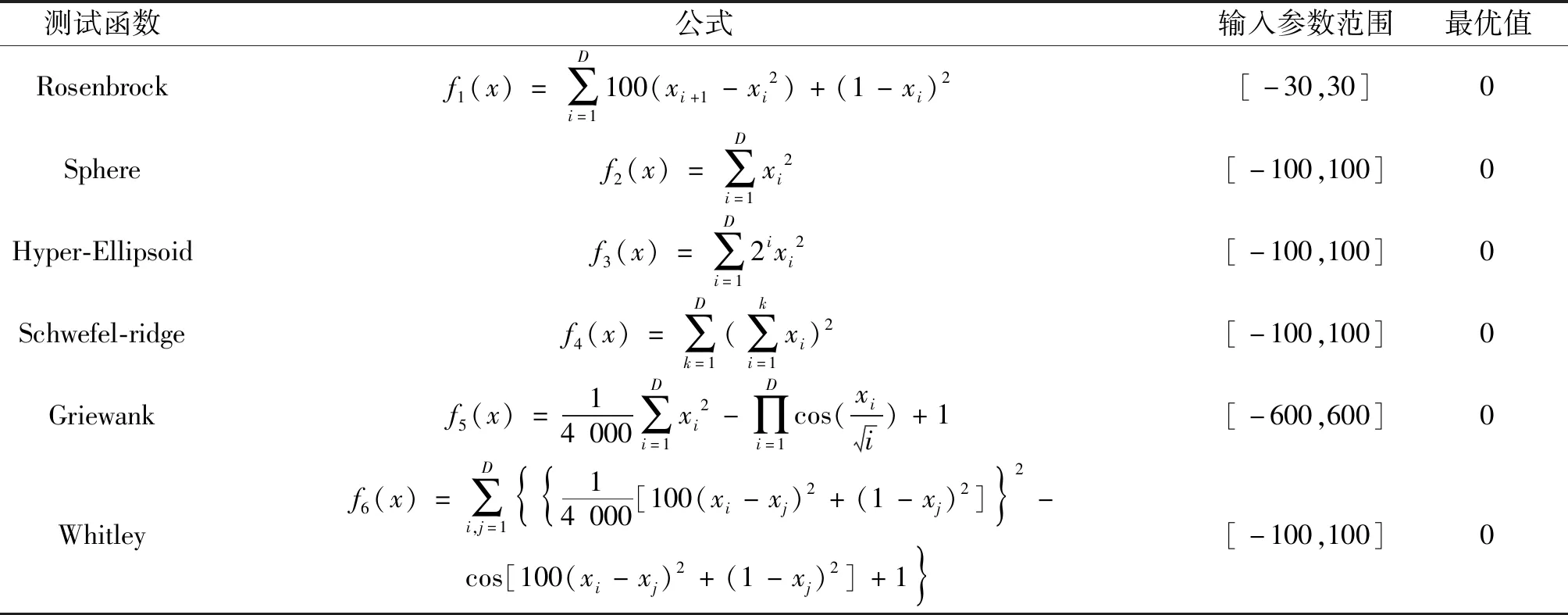

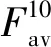
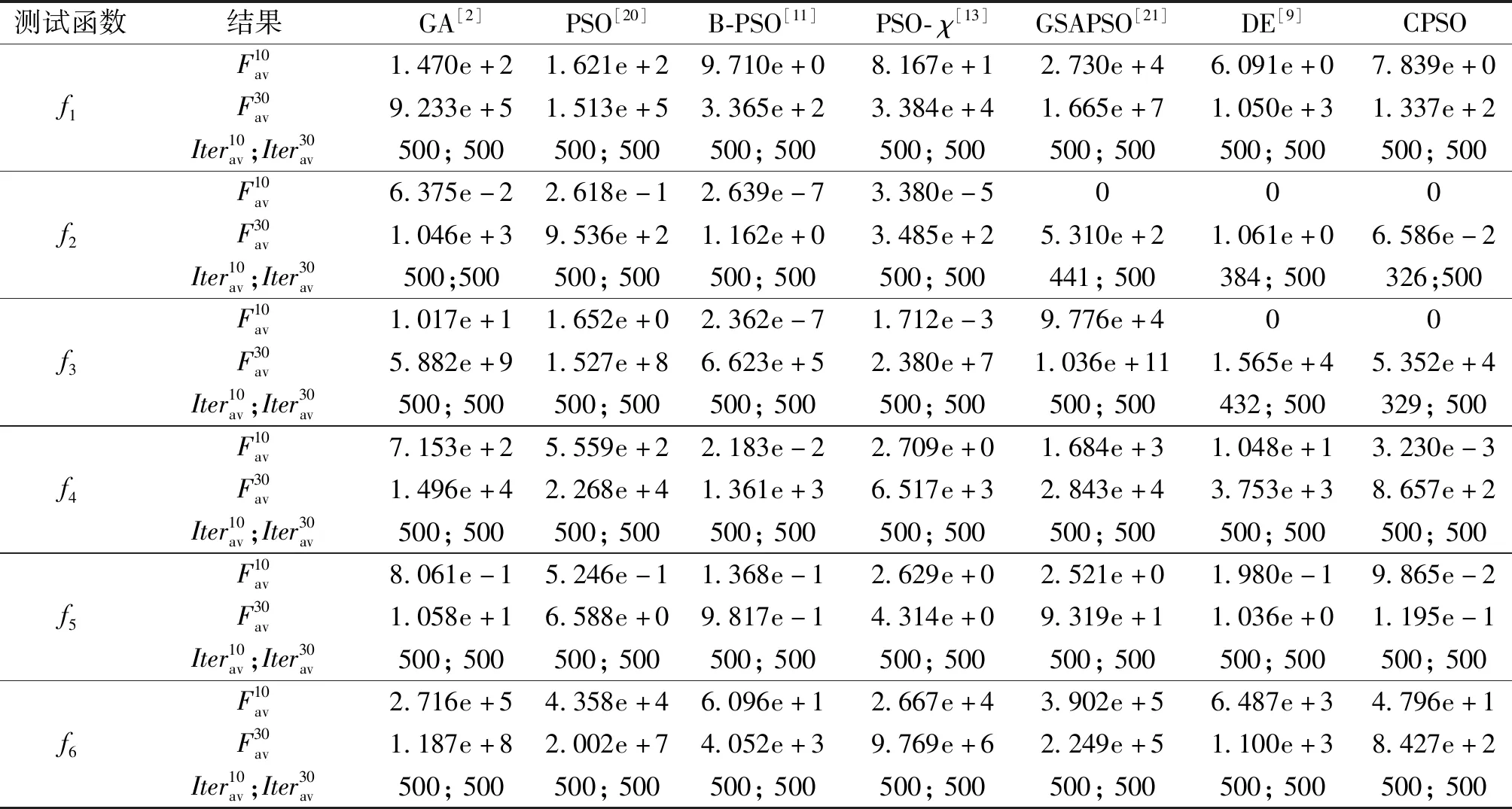
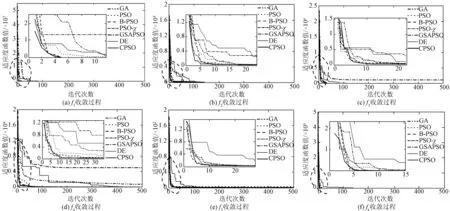
5 PEMFC模型参数辨识
5.1 参数辨识范围
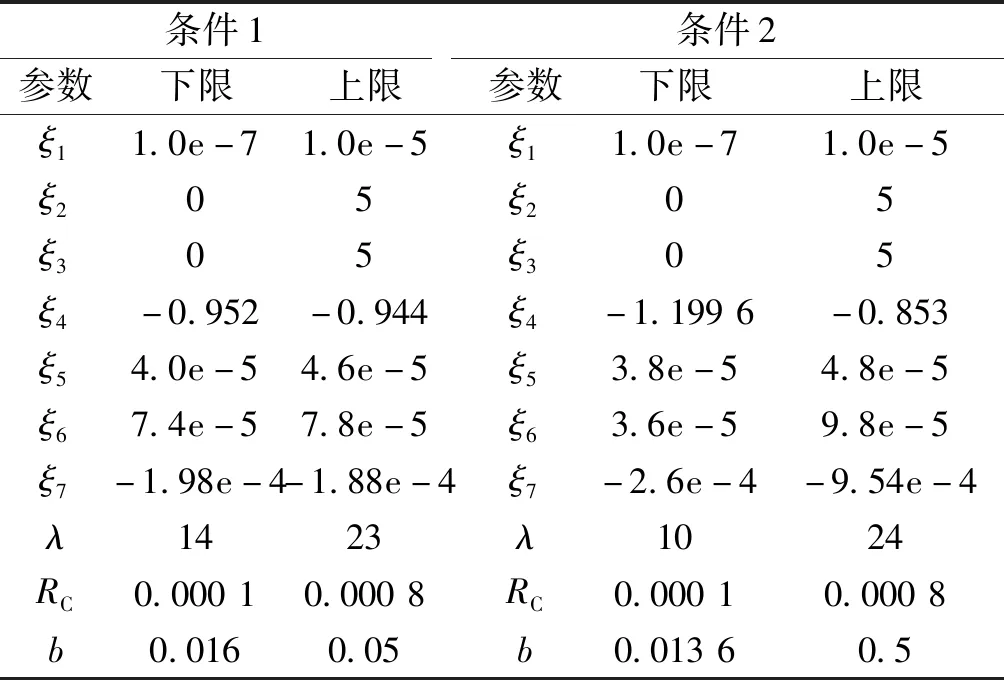
5.2 稳态工况参数辨识结果
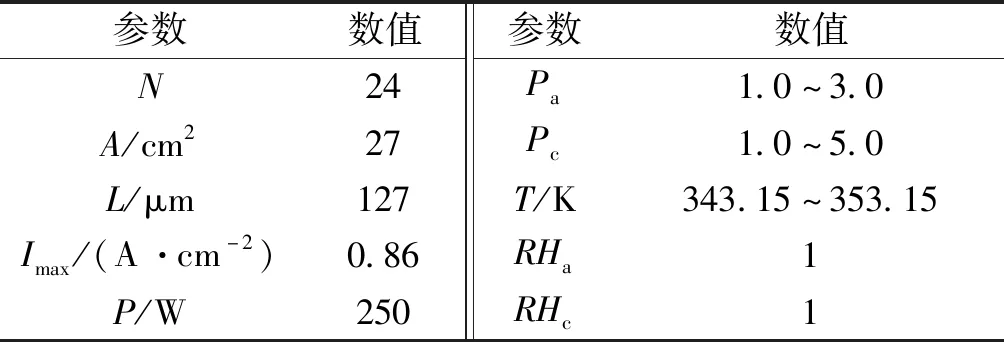


5.3 不同工况下不同模型参数辨识结果
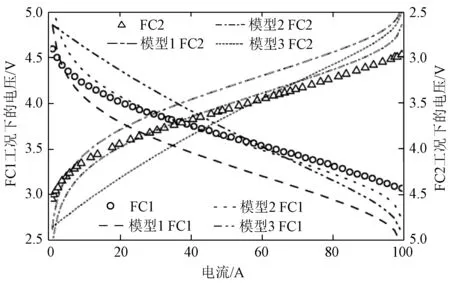
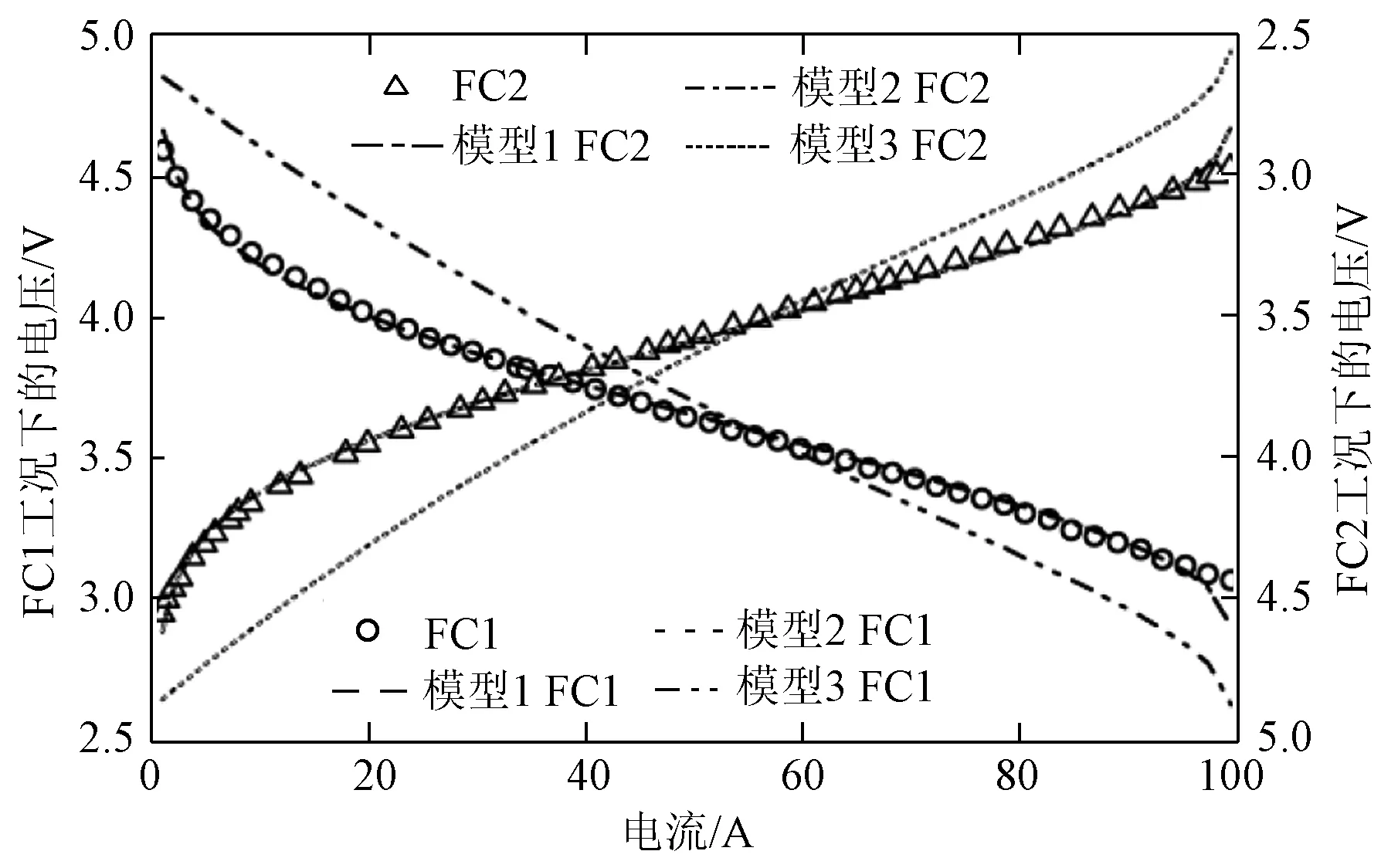
6 结论

