钨柱破片对装甲钢的侵彻研究

张佳玉， 赵太勇， 付建平， 印立魁， 王维占， 孟凡高

(1.中北大学 机电工程学院，太原 030051； 2.中北大学 地下目标毁伤技术国防重点学科实验室，太原 030051;3.山东北方滨海机器有限公司，山东 淄博 255000)

弹丸能否击穿防护装甲是对弹丸威力最为严苛的考验。破片杀伤战斗部作为现役战斗部的主要类型之一，主要依靠战斗部内高能炸药爆炸后产生的爆轰波驱动破片向四周飞散，高速破片和爆轰波用于杀伤敌方有生力量、击穿破坏装甲车辆、舰船、拦截导弹等[1-3]。装甲钢因具有良好的抗弹侵彻能力、抗冲击能力和抗崩落能力，以其优越的性能现仍为防护最常见的装甲[4]；而钨合金材料力学性能好、加工工艺可控，现已被作为预制毁伤元广泛应用在杀爆战斗部内。在有限的空间内，钨柱破片相对于钨球破片可以实现更大的战斗部装填比，存速能力也较好，且不易跳弹，然而不同着靶姿态的柱形破片侵彻能力有较大差异，这也是杀爆战斗部设计必须考虑的问题，所以研究其不同着靶姿态下的弹道极限速度(V50)具有非常重要的意义。

关于柱形破片不同着靶姿态侵彻靶板的研究较少，戴喜会等[5]通过试验和数值模拟的方法研究了长径比及着靶姿态对钨柱破片极限贯穿速度的影响，柱形破片长径比和着靶姿态是影响极限贯穿速度的重要因素，破片质量一定条件下，当长径比为0.8时，极限贯穿速度受破片着靶姿态的影响较小，当长径比大于1.2，极限贯穿速度受破片着靶姿态的影响非常明显。王鹏等[6]在对钨柱正侵彻装甲钢板试验中发现钨柱的着靶姿态主要有：纵向着靶、斜着靶、横向着靶3种姿态，不同着靶姿态的破片极限穿透特征有较大差异。刘俊等[7]通过数值模的方法研究了柱形破片侵彻钢靶的极限穿透速度和穿透剩余速度。结果表明：破片着靶姿态是影响极限穿透速度与剩余速度的重要因素。虽然前人对柱形破片不同着靶姿态的侵彻能力做了一定的研究，但对不同着靶姿态下柱形破片的极限穿透速度受破片质量、破片材料、破片形状、破片长径比等的研究任然不足。鉴于此，本文通过试验与数值模拟相结合，对比不同质量的钨柱破片以不同着靶姿态侵彻10 mm厚装甲钢的弹道极限速度，探索不同质量、不同着靶姿态角钨柱破片的弹道极限速度，以及不同质量、不同着靶姿态角对弹道极限速度的影响规律。

1 试验研究

试验采用12.7 mm滑膛弹道枪发射钨柱破片，弹道枪及试验场地如图1所示。钨柱破片通过弹托加载，弹托出枪口后在空气阻力作用下与破片分离[8]。靶板前设置一对线圈靶，测量破片撞靶前初速。

(a) 12.7 mm弹道枪

试验破片材料为93w，钨柱直径7 mm、高7 mm、质量为5 g，抗压强度大于4.28 kN，弹托为尼龙，如图2所示[9]。

(a) 钨柱破片

表1分别为钨柱破片纵向和横向正侵彻10 mm装甲钢试验结果。剔除无效试验数据，1～6为钨柱破片纵向正侵彻试验数据，7～12为钨柱破片横向正侵彻试验数据。

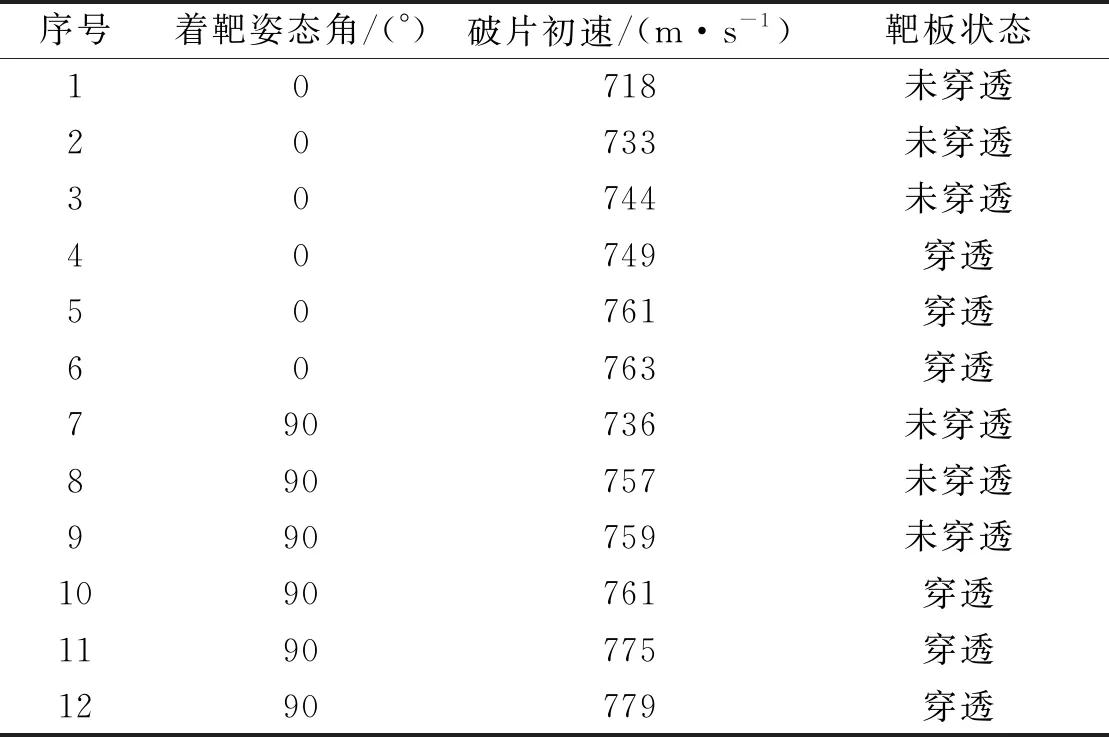
表1 钨柱破片侵彻10 mm装甲钢试验数据表

对于弹道极限速度，通常理解为弹体以规定着角贯穿给定类型和厚度的靶体所需要的撞击速度。以美军弹道极限标准：弹体能在靶板上穿出一个通孔，但靶后没有飞散破片的最低速度。试验采用6射弹弹道极限的方法获取钨柱破片极限穿透速度，该方法为：获取某一规定速度差值范围内的3发完全贯穿和3发局部侵彻数据计算弹道极限。由表1可知，试验中1～6发、7～12发速度最大差值都在45 m/s以内，符合6射弹弹道极限的方法要求。求取3发最小的完全贯穿和3发最大的局部侵彻速度的平均值，可以确定5 g钨柱破片纵向正侵彻10 mm装甲钢极限穿透速度为745 m/s，横向正侵彻10 mm装甲钢极限穿透速度为761 m/s。

表2为钨柱破片斜侵彻10 mm装甲钢试验数据。

表2 几种姿态角下钨柱破片侵彻10 mm装甲钢试验数据表

破片在弹道枪膛内加载速度阶段，破片受弹托约束，姿态基本保持不变，出枪口后，当破片具有不同姿态角时，由于钨柱破片前端面和侧面受空气阻力作用不同，破片在飞行过程中极可能发生较大偏转，较难判定着靶时的准确姿态[10]。试验中如果通过控制加载破片姿态角而控制其着靶姿态角也较难实现。表2为试验中以43°～47°姿态角加载的3发正侵彻5 g钨柱破片，但其穿靶状态存在差异。通过数值模拟观察破片变形状态，发现其分别与40°，60°，70°着靶姿态角数值模拟结果吻合较好。对比表1和表2可发现表2中斜着靶钨柱破片击穿装甲钢靶所需要的速度更大，可以明显看出着靶姿态对钨柱破片极限穿透速度有一定影响。

2 数值模拟研究

柱形破片和靶板形状、材料特性、几何尺寸直接影响破片击穿靶板的极限穿透速度[11]。当这些特性都一样时，极限穿透速度主要与破片着靶姿态有关。要完成不同尺寸柱形破片以不同着靶姿态侵彻装甲钢的试验需要大量的工作，试验成本高、周期长、进度慢，具有局限性，但如今随着计算机数值模拟模拟技术的不断进步，许多试验都可以通过数值模拟来扩展延伸并得到可靠的结果。柱形破片主要有纵着靶、斜着靶、横着靶，柱形破片着靶姿态如图3所示，图3中：θ为着靶姿态角。在试验基础上，采用数值模拟方法计算3 g，5 g，8 g 3种柱形破片以不同着靶姿态侵彻10 mm厚装甲钢的极限穿透速度。钨柱破片尺寸如图4所示。

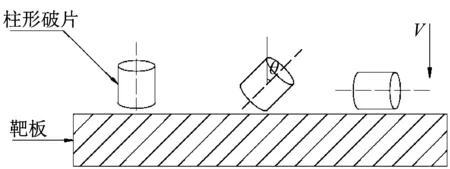
图3 柱形破片竖、斜、横着靶姿态示意图

(a)

2.1 建模建立

弹靶模型采用Truegrid建立标准六面体网格模型，破片尺寸如图4所示，靶板尺寸为85 mm×85 mm×10 mm。柱形破片采用蝴蝶形网格[12]，为保证弹靶接触部分网格尺寸均匀，靶板中心加密，弹靶接触部分网格尺寸为0.46～0.68 mm，由于靶板边缘网格对计算精度影响较小，边缘网格大小为中心网格的2倍，靶板边界设置无反射边界条件，弹靶网格如图5所示。采用LS-DYNA软件作为数值模拟软件，算法为Lagrange算法，单位为cm-g-us制，破片与靶板之间设置侵蚀接触。

2.2 材料参数

装甲钢和93钨的材料模型均采用Johnson-Cook本构材料模型，材料参数见表3和表4。其中:ρ为密度;G为剪切模量;A为屈服应力;B为硬化系数;n为硬化指数;c为应变率系数;M为温度系数;TM为融化温度;TR为环境温度;D1～D5为影响材料变形的失效参数。

表3 装甲钢Johnson-Cook材料模型参数[13]

表4 93钨Johnson-Cook材料模型参数[14]

2.3 结果分析

表5为数值模拟得到的不同着靶姿态角下3种钨柱破片侵彻10 mm厚装甲钢弹道极限速度值。

表5 钨柱破片数值模拟弹道极限速度

2.3.1 经典公式验证

穿甲动力学关于弹丸弹道极限速度的经验公式较多，涉及参数也较多，计算弹丸弹道极限速度主要与弹丸的尺寸、材料、速度，以及靶板的材料、厚度等有关[15]。除破片纵向正侵彻外，通过公式计算其他着靶姿态钨柱破片的弹道极限速度较难实现。式(1)为经典De Marre公式，该公式可用于计算钨柱破片纵向正侵彻靶板的弹道极限速度。

(1)

式中：ms为弹丸质量;Dp为弹径;T为靶板厚度;A为考虑装甲性能和弹体结构影响的修正系数。通过试验得知：A的取值为2 000～2 600[16]，这里取A=2 400。理论计算值与数值模拟值对比如表6所示。

表6 极限穿透速度理论值与数值模拟值对比表

理论计算与数值模拟结果的相对误差在10%以内，认为数值模拟数据较为可靠。

2.3.2 试验结果验证

表7为不同着靶姿态下钨柱破片穿靶后形状的试验与模拟结果对比。

表7 试验破片与数值模拟破片形状对比表

由表7可知，钨柱破片在侵彻装甲钢过程中，破片被横向镦粗，破片弹靶接触部分不断被磨蚀，并挤压迫使破片头部质量不断向作用区域周围不均匀翻卷，最终沿破片周向形成不规则蘑菇头状翻边，试验和数值模拟得到的钨柱破片形状较为相似。

表8为5 g钨柱破片试验与数值模拟弹道极限速度对比，由表8可知，两者相对误差在5%左右，满足工程误差要求。

表8 5 g钨柱破片试验与数值模拟V50对比表

2.3.3 侵彻过程分析

由数值模拟结果可以发现，3种质量破片均在50°着靶姿态角时破片极限穿透速度最大。提取数值模拟5 g钨柱破片分别以0°,50°,90°姿态角临界穿靶状态下加速度、速度变化曲线，如图6、图7所示。

图6 5 g钨柱破片0°,50°,90° 3种姿态加速度衰减图

图7 5 g钨柱破片0°，50°，90° 3种姿态速度衰减图

以0°,50°,90°着靶姿态角分别对应于纵、斜、横3种着靶状态，通过对纵、斜、横3种状态下钨柱破片侵彻装甲钢加速度、速度变化来描述侵彻过程。

由图6、图7可以对钨柱破片侵彻装甲钢靶板过程做如下分析：

a～b段，破片从刚接触靶板开始侵入靶板，侵彻初期，钨柱破片速度大，动能高，侵彻阻力大，加速度大，速度衰减最快，其中纵着靶和横着靶弹靶接触面积大，阻力大，速度衰减曲线斜率最大，破片速度下降最快。斜着靶为破片棱角最先侵彻靶板，初始阻力较小，斜着靶速度损失较慢，破片能瞬间嵌入靶板且不易跳弹[17]。

b～c段，破片由前端小部分侵入靶体到破片大部分侵入靶体，斜着靶破片中间段横截面大，质量集中，此间段斜着靶破片会受到较大的阻力，破片速度衰减快，破片纵着靶和横着靶速度衰减相对较慢。

c～d段，钨柱破片完全侵入靶体，并在靶内持续做侵彻运动。破片主要受到沿速度方向的轴向抵抗力和破片头部周向的挤压力。侵彻过程中，破片被横向镦粗，前端头部不断被磨蚀，并挤压迫使破片头部质量不断向弹靶作用区域周围不均匀翻卷，最终沿破片周向形成不规则蘑菇头状翻边。此阶段，由于钨柱破片靶内运动过程中破片周围不断被磨蚀，弹靶接触面大小逐渐趋于稳定。钨柱破片靶内运动过程中最大横截面越大，受到靶板的抵抗力越大，越不利于击穿靶板。斜着靶破片由于靶内运动过程中头部横截面最大，受靶体抵抗力最大，速度衰减多，横着靶破片次之，纵着靶最小。

d～e段，破片击穿靶体，靶体出现通孔，钨柱破片速度也衰减为0。

通过以上对侵彻过程受力、加速度、速度变化分析可以得到：钨柱破片斜着靶侵彻装甲钢靶时，破片所受的阻力先增大后减小。a～b段，斜着靶破片阻力小于纵、横着靶破片阻力；b～c段，斜着靶破片阻力大于纵、横着靶破片阻力；c～d段，斜着靶破片阻力微大于纵、横着靶破片阻力。不同着靶姿态钨柱破片侵彻装甲钢靶主要不同在于破片侵彻靶板初期阶段(前20 μs)。

2.3.4 破片质量、着靶姿态角与V50的关系

杀爆战斗部爆炸后，破片毁伤元在瞬间的高压爆轰场作用下迅速加载速度[18]。对于柱形破片，破片从爆炸起始端到达目标靶过程中，会受到较为复杂的空气阻力作用，破片飞散姿态不一，破片着靶姿态也各有不同[19]。在弹靶材料、形状、几何尺寸不变的条件下，柱形破片弹道极限速度受着靶姿态影响较大。这与破片不同着靶姿态时破片迎风面积有较大关系，计算柱形破片迎风面积式(2)如下，图8为3 g，5 g，8 g钨柱破片不同着靶姿态下破片迎风面积变化曲线。

图8 钨柱破片迎风面积变化曲线

A=πR2cosθ+2Rlsinθ

(2)

试中：A为柱形破片空气中飞行迎风面积；θ为破片轴线与靶板法线的夹角；R为柱形破片圆半径。

图9为由表5得到的破片着靶姿态角-弹道极限速度图。

图9 破片着靶姿态角-弹道极限速度图

对比图8和图9可以发现不同着靶姿态柱形破片极限穿透速度与破片迎风面积呈正相关。

图10为破片质量-弹道极限速度图。

图10 破片质量-弹道极限速度图

由图10破片质量与弹道极限速度关系图可以看出，破片质量越小，弹道极限速度越大。同质量破片当着靶姿态角为0°时，钨柱破片迎风面积最小，弹道极限速度最小；当着靶姿态角为40°～60°时，钨柱破片迎风面积最大，弹道极限速度大。不同着靶姿态下，对于3 g钨柱破片，最大弹道极限速度比最小弹道极限速度上升4.98%，5 g破片上升3.51%，8 g破片上升2.62%。3 g破片不同着靶姿态角下，破片最大与最小弹道极限速度差值较大，5 g相对小些，8 g破片更小，破片质量越大，破片着靶姿态对其弹道极限速度影响越小，大质量破片对着靶姿态不敏感。

3 结 论

本文通过弹道冲击试验与数值模拟研究着靶姿态对钨柱破片侵彻装甲钢V50影响规律，获得如下结论：

(1) 试验通过6射弹弹道极限的方法得到长径比为1，质量为5 g，93w柱形破片纵向正侵彻10 mm装甲钢的V50为745 m/s，横向正侵彻10 mm装甲钢的V50为761 m/s，并通过数值模拟得到了3 g，5 g，8 g 3种钨柱破片不同着靶姿态下侵彻装甲钢靶板的弹道极限速度。

(2) 钨柱破片斜着靶侵彻装甲钢靶时，破片所受的阻力先增大后减小。不同着靶姿态钨柱破片侵彻装甲钢靶主要不同在于破片侵彻靶板初期阶段(前20 μs)。

(3) 钨柱破片侵彻装甲钢的V50存在波动区间，不同着靶姿态下，钨柱破片V50与破片迎风面积大致呈正相关。当着靶姿态角为0°时(纵向着靶)，钨柱破片迎风面积最小，V50最小；当着靶姿态角为40°～60°时，钨柱破片迎风面积大，V50较大。不同着靶姿态下，对于3 g钨柱破片，最大V50比最小V50上升4.98%，5 g破片上升3.51%，8 g破片上升2.62%。随着破片质量的增加，钨柱破片穿透装甲钢的V50对着靶姿态越不敏感，V50波动区间越小。