服役条件下提速地铁车辆的横向运动稳定性研究

吴俊汉， 文永蓬,3， 宗志祥， 周 月， 董昊亮

(1.上海工程技术大学 城市轨道交通学院,上海 201620； 2.上海市轨道交通振动与噪声控制技术工程研究中心,上海 201620； 3.西南交通大学 牵引动力国家重点实验室,成都 610031；4.上海地铁维护保障有限公司车辆分公司,上海 200235)

随着我国经济的高速发展，地铁覆盖地域不断扩张，地铁车辆提速成为必然趋势，更高的运营速度成为人们关注的重点[1]。在服役条件下，随着轮轨磨损的加剧，会导致车辆的横向运动稳定性裕量不足，对低速地铁车辆可以通过日常的轮轨镟修来维持正常运行，但由于地铁车辆本构的局限，一旦进行提速，可能会出现剧烈的横向振动，影响行车安全性和舒适性。现役地铁车辆由于成本问题不可能完全放弃，因此，服役条件下地铁车辆提速可能产生的横向运动稳定性问题引起了学者的广泛关注[2]。

近年来，国内外学者对轨道车辆的横向运动稳定性进行了大量的研究。蛇行运动是轨道车辆的特有现象，蛇行运动临界速度是衡量车辆横向运动稳定性的重要指标[3]。Zhang等[4]建立了二自由度轮对横向动力学模型，给出了轮对系统的分岔图、相图、庞加莱截面和李雅普诺夫指数，并研究了车轮踏面锥度对Hopf分岔类型的影响。Yan等[5-6]建立了转向架横向模型，研究了等效锥度的变化对线性和非线性临界速度的影响。Dong等[7]建立了半车横向模型，发现了车辆系统存在亚临界和超临界Hopf分岔，并通过根轨迹法求解了Hopf分岔点。Zhang等[8]建立了完整的17自由度高速铁路车辆横向模型，利用特征值分析、分岔图和第一Lyapunov系数对蛇行运动稳定性进行了研究。姜培斌等[9]建立了高速列车刚柔耦合车辆模型，探讨了车辆系统与特定波长的轨道不平顺激励发生的共振特性。Zeng等[10]研究了车辆在直线和曲线轨道上的蛇行稳定性，并分析了曲线轨道半径和轨道超高对车辆临界速度的影响。李凡松等[11]针对动车组车辆偶然出现的抖车现象，发现动车组在服役过程中，车轮与钢轨匹配关系出现异常，导致轮对等效锥度增大，使得转向架蛇行运动频率与车体一阶菱形模态频率发生共振，提出了可以通过打磨钢轨和镟修车轮来改善轮轨匹配关系或者提高车体的一阶菱形模态频率，来提升动车组车体对磨耗车轮和异常线路的适应性。宫岛等[12]通过长期跟踪测试发现，服役条件下的车轮等效锥度过大是车辆发生车体抖振的原因，提出了基于正交试验的多目标车辆系统悬挂参数优化方法，对悬挂参数进行优化设计，提高了车辆运动稳定性及运行平稳性。滕万秀等[13]仿真研究了高寒动车组在-40 ℃低温环境下的动力学性能，服役环境下悬挂参数的改变会使转向架与车体发生共振，导致车辆发生横向晃动。张卫华等[14]研究了车辆结构特征和系统参数对高速列车运动稳定性的影响，考虑系统参数的非线性影响和服役特性，将临界失稳速度为设计目标，给出了车体质量和二系悬挂刚度及阻尼、轴箱纵横向定位刚度等悬挂参数的选择范围，从而实现了高速列车的运动稳定性的提升。李响等[15]分别研究了不同等效锥度的车轮踏面以及悬挂参数的变化对车辆动力学性能的影响，优化计算得出了一组适用于多种高速车辆的局部参数。综上，上述研究中分析了等效锥度变化对车辆横向运动稳定性的影响，但是对服役条件下车轮磨损引起的横向动力学问题重视不足。

为此，论文建立包含抗蛇行减振器的地铁车辆横向动力学模型，通过调研上海某地铁线路的车轮磨损情况，分析服役条件下车轮半径和等效锥度随运营里程的变化规律，获取服役条件下地铁车辆的横向振动特性，研究安装抗蛇行减振器对服役条件下提速地铁车辆横向运动稳定性的提升。

1 含抗蛇行减振器的地铁横向模型及验证

论文建立的地铁车辆横向动力学模型[16]，包括1个车体、2个转向架、4个轮对、连接轮对和转向架的一系悬挂装置、连接车体和转向架的二系悬挂装置、抗侧滚扭杆以及抗蛇行减振器。车辆系统参数及含义如表1所示。

表1 某地铁车辆横向动力学模型的参数

假设车体和转向架之间的受力可简化为由二系悬挂装置提供的纵向、横向和垂向的二系悬挂力、抗蛇行减振器提供的纵向力以及抗侧滚扭杆提供的扭矩，受力情况如图1所示。车体运动包括横移yc、摇头Ψc和侧滚φc，其中横移和侧滚是耦合运动，即滚摆运动，共计3个自由度。根据车体受力关系，得到车体的振动微分方程，分别为

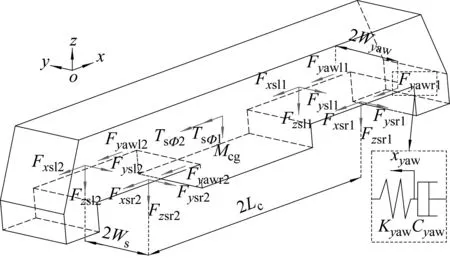
图1 车体的受力示意图

(1)

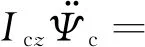
(Fysl2+Fysr2-Fysl1-Fysr1)Lc+

(Fyawl1+Fyawl2-Fyawr1-Fyawr2)Wyaw

(2)

(Fysl1+Fysr1+Fysl2+Fysr2)H1-Tsφ2

(3)

式中:下标x、y、z为纵向、横向和垂向；下标s为二系悬挂；下标yaw为抗蛇行减振器；下标l，r分别为左侧和右侧；Tsφ1，Tsφ2分别为1位端、2位端转向架提供的抗侧滚扭杆力矩。

车体与转向架之间的二系悬挂力及抗侧滚扭杆力矩为

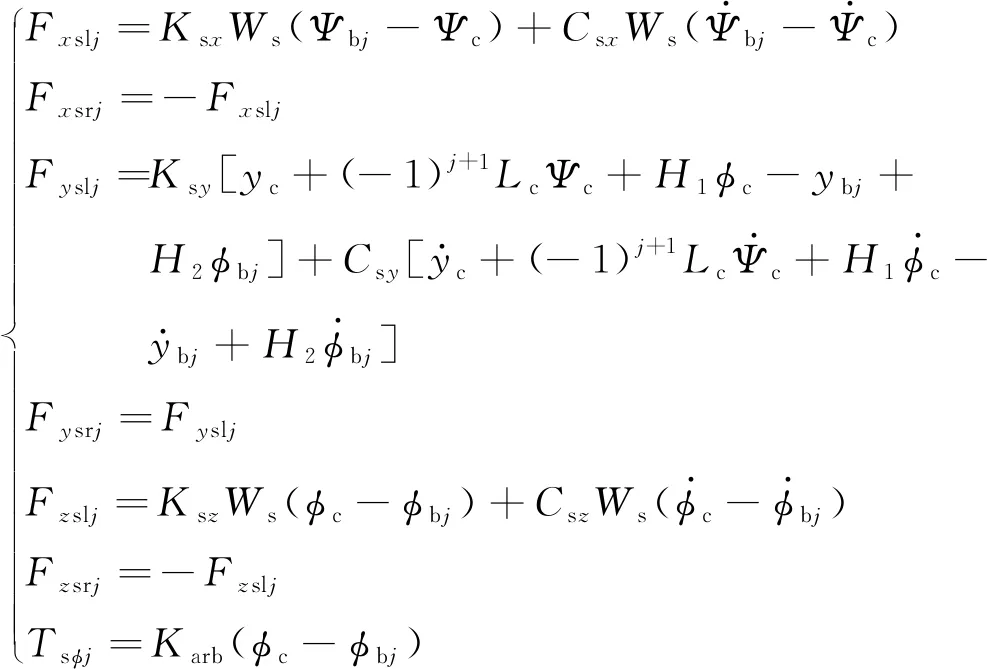
(4)

式中，j为j位端转向架(j=1,2)。

将抗蛇行减振器描述为经典的Maxwell模型，可得到左、右侧抗蛇行减振器弹簧力为

Fyaw(lj,rj)=Kyaw(xyawlj±ΨbjWyaw)

(5)

式中：Kyaw为抗蛇行减振器的刚度；xyaw为抗蛇行减振器阻尼活塞的位移。

左、右侧抗蛇行减振器阻尼力为

(6)

式中，Cyaw为抗蛇行减振器的结构阻尼。

因此，左、右侧抗蛇行减振器的平衡方程为

(7)

构架除了会受到来自车体的反作用力外，还会受到来自构架与轮对之间的一系悬挂力，受力如图2所示。同理，构架运动包括横移ybj(j=1,2)、摇头Ψbj(j=1,2)、侧滚φbj(j=1,2)，共计6自由度。根据构架的受力关系，可得到构架的振动微分方程，分别为

图2 构架的受力示意图

Fyslj+Fysrj-Mbgφbj

(8)

(Fypl(2j)+Fypr(2j)-Fypl(2j-1)-Fypr(2j-1))Lb+

(Fxpl(2j-1)+Fxpl(2j)-Fxpr(2j-1)-Fxpr(2j))Wp+

Wyaw(Fyawrj-Fyawlj)

(9)

(Fzpr(2j-1)+Fzpr(2j)-Fzpl(2j-1)-Fzpl(2j-1))Wp+

(Fypl(2j-1)+Fypl(2j)+Fypr(2j-1)+Fypr(2j))H3

(10)

式中，下标p为一系悬挂。

构架与轮对之间的一系悬挂力为

(11)

式中，i为第i轴轮对，当j=1时，i=1,2，当j=2时，i=3,4。

轮对除了会受到来自构架的反作用力外，还会受到轮轨之间的蠕滑力、蠕滑力矩和轮轨法向力，受力如图3所示。由于车轮踏面具有锥度，当轮对发生横移时，轮对左右滚动圆半径不同会使轮对产生一个侧滚角，该侧滚角可通过轮对的横移量线性表示，故不单独考虑轮对的侧滚，仅考虑轮对的横移ywi(i=1,2,3,4)、摇头Ψwi(i=1,2,3,4)，共计8自由度。根据轮对的受力关系，可得到轮对的振动微分方程，分别为

图3 轮对的受力示意图

Fypli+Fypri-Mwgφwi-FRi

(12)

(Fcxri-Fcxli)Lw+(Fxpri-Fxpli)Wp+Tczri

(13)

式中:Fcx，Fcy，Tcz分别为纵向蠕滑力，横向蠕滑力和自旋蠕滑力矩；Fn为轮轨法向力；FRi为轮缘力。

根据Kalker线性蠕滑理论[18-19]，轮对所受的蠕滑力以及蠕滑力矩可以表示为

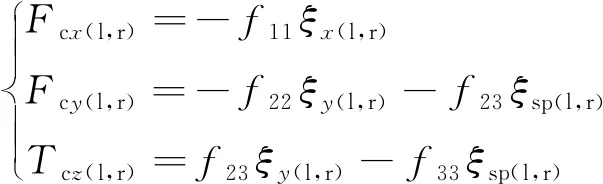
(14)

式中：f11,f22,f23,f33分别为纵向、横向、横向自旋和自旋蠕滑系数；ξx(l,r)，ξy(l,r)，ξsp(l,r)分别为纵向、横向、自旋蠕滑率，考虑轮对横移和摇头的情况下可表示为

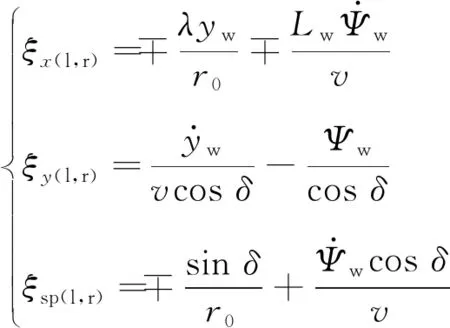
(15)

式中:λ为等效锥度;∓分别为左侧和右侧；v为车辆行驶速度；δ为轮轨接触角。

考虑轮对为锥形踏面时，当轮对发生横移时，轮轨法向力会产生一个横向力来抑制轮对的横移运动，可以表示为

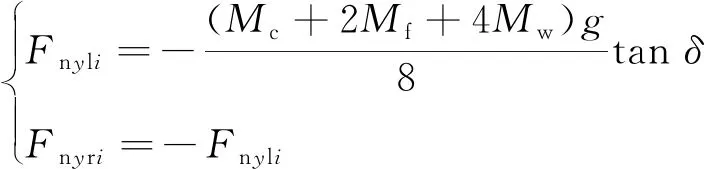
(16)

轮对横移超过轮缘-钢轨间隙时，轮对在会受到轮轨碰撞产生的轮缘力，可以分别表示为

(17)

式中:K0为轮缘和钢轨接触刚度，取K0=1.617×107N/m；Δ为轮缘-钢轨间隙，取Δ=9.23 mm。

对于17自由度横向动力学模型，可以将振动微分方程统一表达为如下的矩阵形式

(18)

式中:M,C,K分别为地铁车辆系统的质量矩阵、阻尼矩阵和刚度矩阵，均为17阶方阵；X为地铁车辆系统的自由度向量，为17×1阶矩阵。

(19)

式中:A为地铁车辆系统的雅可比矩阵，是与车速v相关的34阶方阵;E为单位矩阵。

根据运动稳定性理论，判断车辆系统是否稳定，可以通过系统的雅可比矩阵特征值实部的正负号来判断。计算系统雅可比矩阵的特征值，使

|λ(v)E-A(v)|=0

(20)

式中，λ(v)为雅可比矩阵的特征值。

若存在v，使得雅可比矩阵最大特征值实部满足

Reλ(v)≥0

(21)

那么，最大特征值实部为零的速度为蛇行临界速度。

根据表1参数，采用特征值法计算蛇行临界速度，如图4所示。图4中，最大特征值实部小于零时系统稳定，最大特征值实部大于零则系统失稳，可见，蛇行临界速度约为124 km/h。

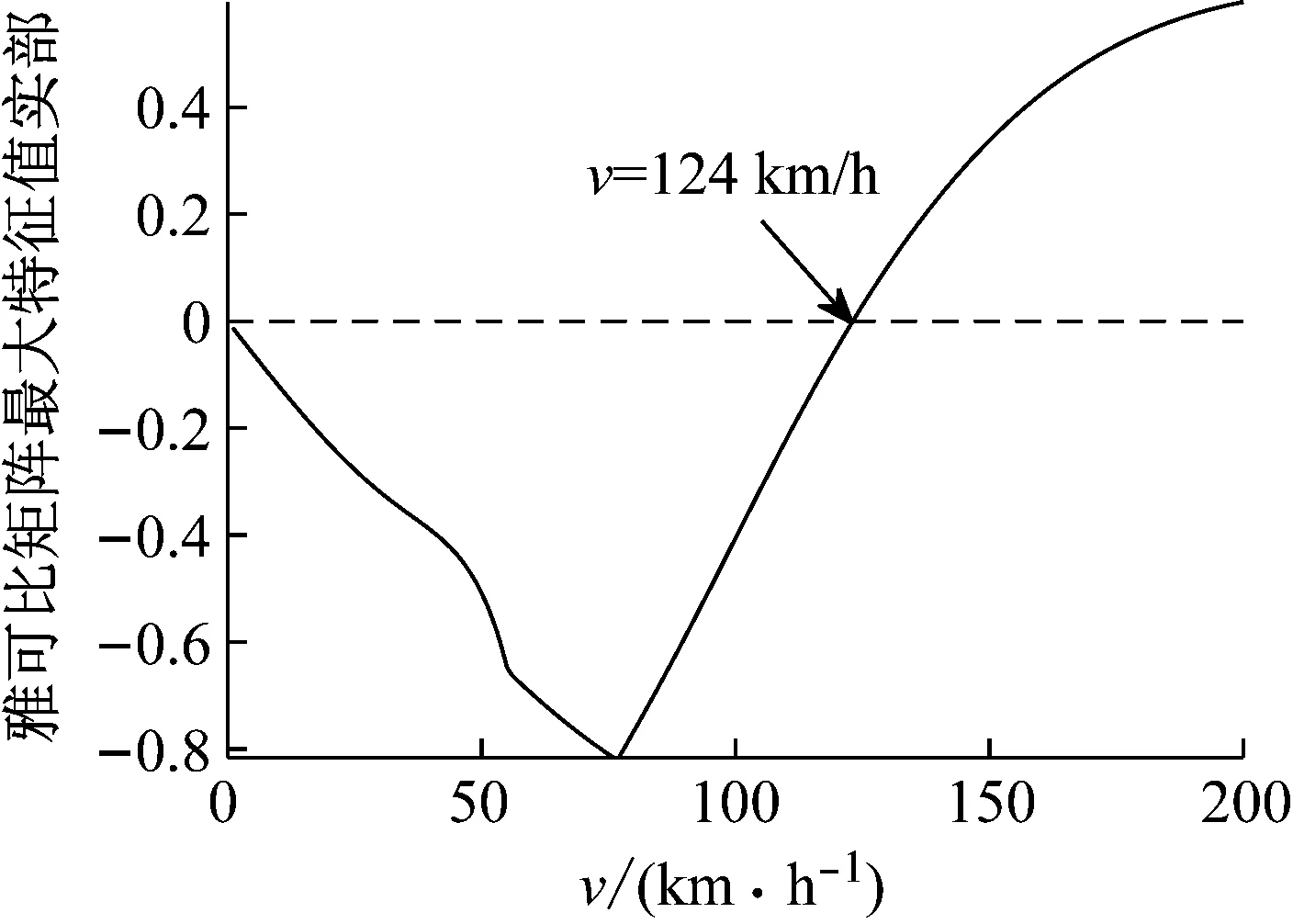
图4 特征值法求解临界速度

为了验证该临界速度的可靠性，根据表1参数建立了基于SIMPACK软件的地铁车辆模型，如图5所示。

图5 基于SIMPACK软件的地铁车辆动力学模型

采用根轨迹法计算车辆系统的阻尼比，可以求解地铁车辆的临界速度，如图6所示。

由图6可知，地铁车辆的蛇行模态对应系统的最小阻尼比，当最小阻尼比小于零时，车辆系统会发生蛇行失稳，即该车辆的临界速度为131.5 km/h，与特征值法求解的临界速度误差为5.7%，原因可能是SIMPACK建立的是空间模型，与论文建立的横向模型存在可能误差，但从结果来看，两者求解的临界速度是接近的。

(a) 蛇行模态分布

通过论文模型进行数值积分，求解车辆横向动力学方程得到的车速与轮对横移的分岔图，如图7所示。由图7可知，车速在135 km/h前，轮对横移幅值趋近于0，超过该速度后，轮对横移幅值发生陡增，因此，135 km/h为数值法求得的蛇行运动临界速度。该临界速度与特征值法求得的临界速度误差8.1%，与SIMPACK求解的临界速度误差仅2.6%，说明数值积分求得的动力学响应是可靠的，可以用于进一步的仿真分析。

图7 车速-轮对横移分岔图

综上，通过特征值法、根轨迹法求解地铁车辆的临界速度，其结果与论文模型的数值模拟结果基本一致，从而证明了论文模型的正确性。

2 地铁车轮磨损调研

地铁车轮磨损是一个逐步累积的随机过程[20]。车轮在磨损过程中不仅会改变车轮半径，往往还伴随着等效锥度的变化，具有动态时变性和随机性[21]。通过对上海某线路车辆进行了长期的调研，得到了车轮磨损随运营里程变化的实际数据。不同车辆各轴车轮半径随运营里程增加的变化图,如图8所示。

(a) 车辆1

由图8可知:服役条件下，车轮半径并非随运营里程的增加而线性减小，同一车辆各车轮半径演化在短运营里程内存在一定的相似性；不同车辆之间存在车轮磨损前期车轮半径磨损速度较快，车轮磨损后期车轮半径磨损速度减慢，原因可能是磨耗型踏面有利于减缓车轮半径的磨耗。总体来看，轮对的半径会随着运营里程的增加而不断减小。

由于地铁车辆通常采用的是锥形车轮，导致踏面各位置的受力差异较大，使得踏面出现不均匀的磨耗，导致车轮锥度发生改变。考虑轮对横移量3 mm处的等效锥度随运营里程增加的变化，如图9所示。由图9可知，当运营里程较小时，等效锥度分布在0.05附近，等效锥度随运营里程的增加呈上升的趋势。调研发现等效锥度存在个别异常值，造成的原因可能是计算等效锥度需准确测量车轮踏面、轨面、左右车轮半径、轮对内侧距、轨距和轨底坡等尺寸存在人工测量误差[22]；等效锥度偏大值可能是地铁车辆在维护周期内，轮轨关系恶化导致。

图9 等效锥度随运营里程的变化

在服役过程中车轮磨损导致的车轮半径减小和等效锥度增大，会对地铁车辆的横向运动稳定性产生一定影响，下面将具体分析。

3 车轮磨损对车辆横向运动稳定性的影响

3.1 车轮半径对车辆横向运动稳定性的影响

随着运营里程的增加，车轮磨损日益加剧，导致车轮半径减小。为探究车轮磨损对车辆运动稳定性的影响，论文给出了新旧车轮在不同速度下的轮对横移相图，如图10所示。

(a) 135 km/h

当车速135 km/h时的新旧车轮横移相图，见图10(a)，该速度为新车轮的临界速度，故新车轮的横移幅值收敛于原点附近，而磨损车轮迅速发散形成了稳定的极限环，说明此时磨损车轮已经发生了周期性的蛇行运动，可以初步判断，磨损车轮相较于新车轮具有更低的临界速度，更易导致车辆失稳。当车速140 km/h时的新旧车轮横移相图，见图10(b)，已经超过了新车轮的临界速度，可以明显看出，新旧车轮都形成了稳定的极限环，但磨损车轮形成的极限环无论从横移幅值还是横移速度，均大于新车轮，即该速度下磨损车轮发生更剧烈的蛇行运动。因此，服役条件下车轮半径的减小，会降低车辆的横向运动稳定性。

进一步地，研究了随车轮半径变化的车速-轮对横移分岔，获得了轮对横移幅值与车速、车轮半径的关系，如图11所示。

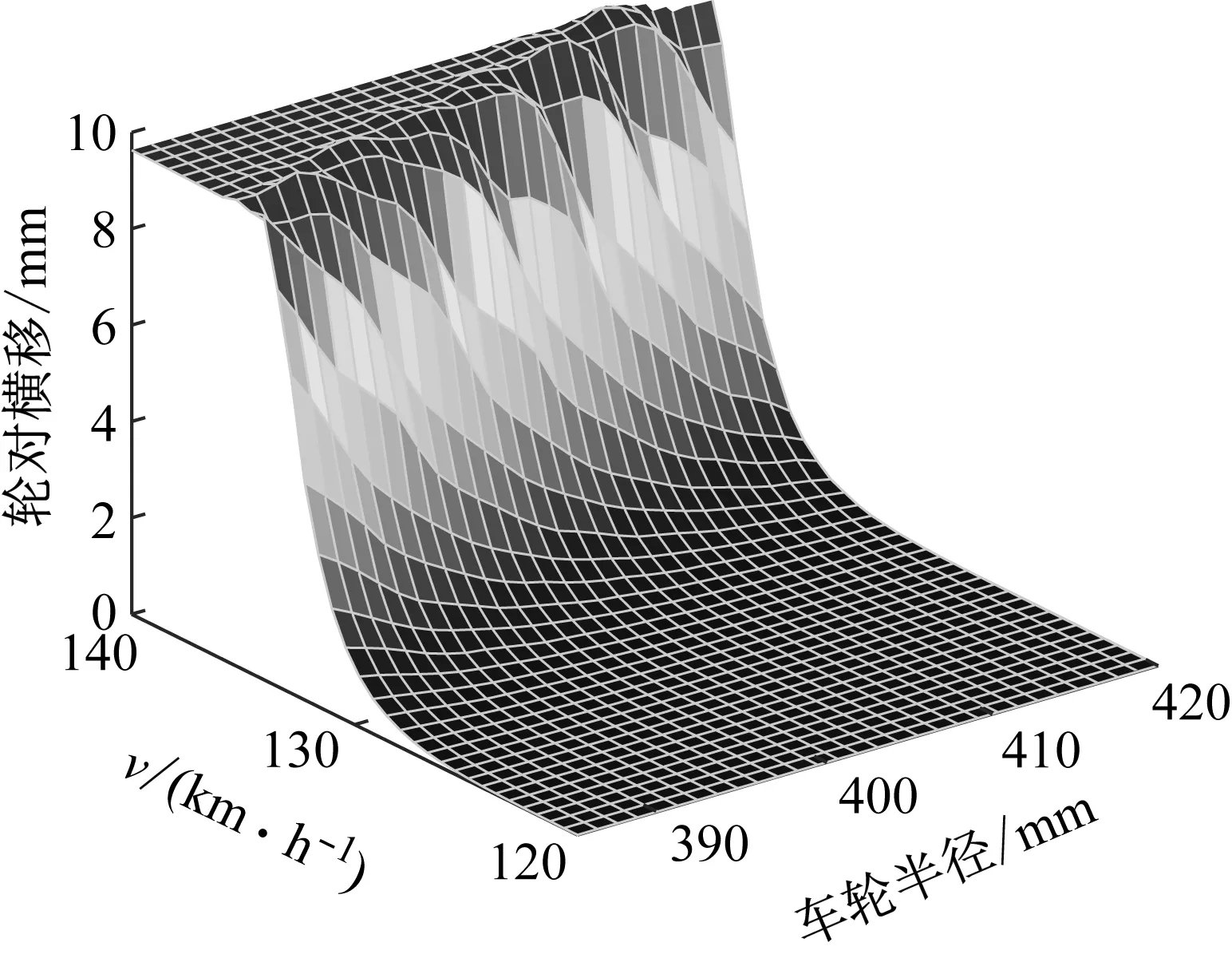
图11 轮对横移幅值随车速、车轮半径变化图

由图11可知，图像呈阶梯状分布，随着车轮半径的减小，轮对横移幅值更快达到峰值，说明磨损后的轮对在更低的速度下就会发生蛇行失稳，这意味着车轮半径减小会降低地铁车辆的临界速度，影响车辆的横向运动稳定性。

3.2 等效锥度对车辆横向运动稳定性的影响

等效锥度作为衡量轮轨接触关系的重要指标，与车辆的横向运动稳定性密切相关[23]。图12为随等效锥度变化的车速-轮对横移分岔图。

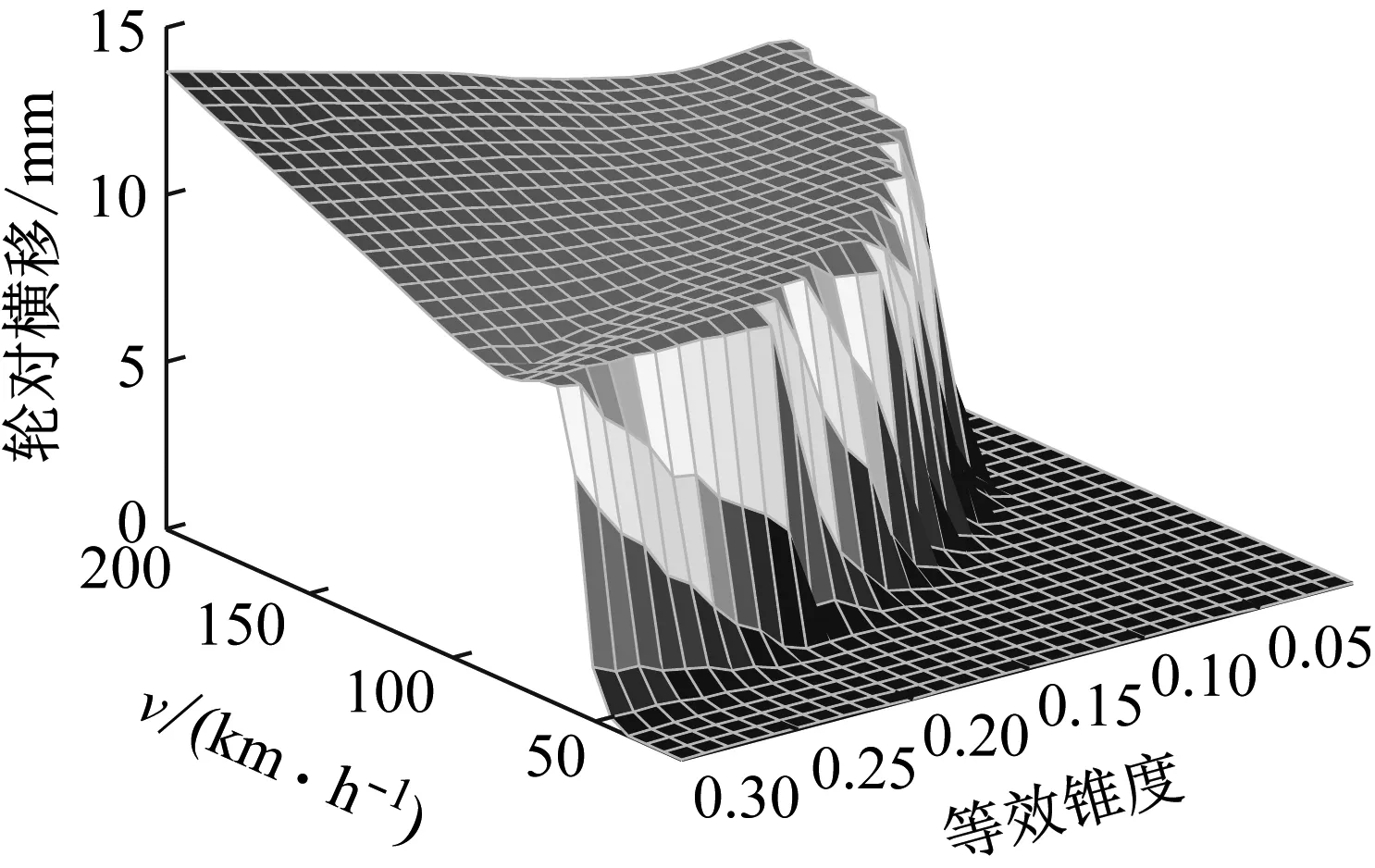
图12 轮对横移幅值随车速、等效锥度变化图

由图12可知:当等效锥度较小时，车辆具有较高的临界速度；随着等效锥度的增大，轮对横移幅值更容易达到峰值，车辆的临界速度降低；同一速度下，随着等效锥度的增大，轮对的横移幅值逐渐增大，说明等效锥度的增大不仅会降低临界速度，同时还会加剧蛇行运动，不利于行车安全。

对于没有安装抗蛇行减振器的地铁车辆，只能通过镟轮和打磨钢轨的方式来降低等效锥度。虽然低等效锥度下，车辆具有较高的临界速度，但等效锥度也不是越小越好。例如当等效锥度为0.01、车速为180 km/h时，悬挂参数异常匹配使车辆系统发生了一次蛇行运动，如图13所示。车辆的蛇行运动不再仅仅表现为转向架失稳的二次蛇行运动，而主要体现在车体失稳的一次蛇行运动。

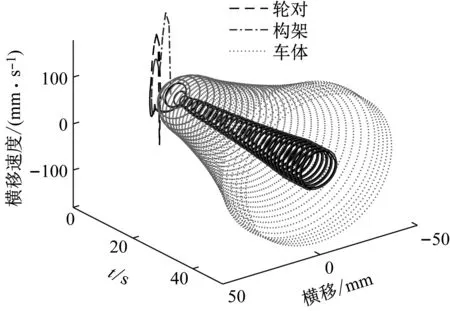
图13 一次蛇行下的轮对、构架和车体横移图

由图13可知：从理论上车体的横移幅值甚至达到了40 mm，远远大于轮对、构架的横移幅值，严重影响了旅客的乘坐舒适性；轮对、构架横移相图形成了半径为10 mm左右的极限环，而车体横移相图形成了半径为40 mm左右的极限环，说明该速度下，轮对，转向架和车体均发生了周期性的蛇行运动。

因此，在车轮镟修和钢轨打磨的过程中，需要严格管理等效锥度和车轮半径。针对现役低速地铁车辆，在车轮随机磨损不可避免减小的情况下，适当控制等效锥度来提高临界速度，能使车辆保持良好的横向运动稳定性。此外，服役条件下，一旦地铁提速，即使是小等效锥度条件，也可能带来的车辆横向运动稳定性裕量不足的问题，因此，下面采用抗蛇行减振器提高地铁车辆的横向运动稳定性。

4 抗蛇行减振器提高地铁车辆的横向稳定性

4.1 抗蛇行减振器参数的选择

由3.1节可知，车轮半径越小、等效锥度越大，车辆的临界速度越小。因此，在低等效锥度下地铁车辆的横向运动稳定性往往具有较大的安全裕量。抗蛇行减振器参数的选取应充分考虑车轮磨损带来的不利影响。因而，研究针对尤其可能引起横向振动失稳的磨损到限车轮和高等效锥度情况，取车轮磨损到限半径为385 mm，等效锥度为0.3。

根据现有研究[24]，大等效锥度下应匹配较小的抗蛇行减振器阻尼，取Cyaw=0.3 MN·s/m。同时，研究表明，不仅抗蛇行减振器阻尼能够起到耗散车辆蛇行运动能量的作用，而且抗蛇行减振器刚度对车辆的横向运动稳定性也有着显著的影响[25-26]。因此，论文接下来在既定的抗蛇行减振器阻尼的基础上，分析抗蛇行减振器刚度变化对车辆临界速度的影响，选取合适的抗蛇行减振器刚度以满足服役条件下地铁车辆提速的横向稳定性需求。

随抗蛇行减振器刚度变化的车速-轮对横移分岔图,如图14所示。由图14可知：随着抗蛇行减振器刚度的增加，轮对横移发生分岔的速度逐渐增大；当刚度较小时，对临界速度的提升较大，而后增速逐渐放缓，说明刚度对临界速度的提高存在上限。为了满足地铁车辆提速的需求，临界速度应大于120 km/h。因此选取对应的抗蛇行减振器刚度Kyaw=3.8 MN/m。

图14 抗蛇行减振器刚度对临界速度的影响

4.2 效果对比与讨论

安装4.1节设计的抗蛇行减振器，研究服役条件下安装抗蛇行减振器对车辆临界速度的提升效果，如图15所示。

图15 抗蛇行减振器效果对比

由图15可知，等效锥度增大是服役条件下临界速度降低的主要原因，车轮半径的减小对临界速度的影响相对较小。安装抗蛇行减振器总体上能够显著提升车辆的临界速度。在车轮磨损前期，即等效锥度在0.05～0.15时，临界速度对等效锥度的变化敏感；当等效锥度较大时，等效锥度增大对临界速度的影响力逐渐下降。在低等效锥度下，未安装抗蛇行减振器的现役地铁能够达到地铁提速要求，但是，等效锥度逐步增大可能将无法满足横向稳定性的要求。

总体看来，在服役条件下，如果未来地铁实施提速，未安装抗蛇行减振器的现役地铁车辆可能引起横向失稳问题；安装抗蛇行减振器能够有效地解决地铁车辆车轮磨损以及提速带来的横向运动稳定性裕量不足问题。

并且，抗蛇行减振器的采用还能让车辆的横向振动具有一定鲁棒性。例如，3.2节提及的在等效锥度为0.01时，悬挂参数异常匹配导致车辆发生了一次蛇行运动，该异常参数车辆安装抗蛇行减振器前后车速与各结构横移的分岔图，如图16所示。

(a) 无抗蛇行减振器

由图16(a)可知，该异常参数下无抗蛇行减振器的车辆临界速度约为165 km/h，主要体现为车体横移过大，即发生一次蛇行运动，超过临界速度后，横移幅值存在一个缓慢提高的过程，说明系统发生的是超临界Hopf分岔。

由图16(b)可知，车辆超过临界速度后，横移幅值立刻发生突变，达到了峰值，说明系统发生的是亚临界Hopf分岔，从行车安全的角度考虑，这种突变现象的发生是应该避免的。但是，含抗蛇行减振器的车辆临界速度高达305 km/h，较无抗蛇行减振器的车辆提升了84%之多，且超过临界速度后车体的横移小于构架和轮对的横移，没有发生一次蛇行运动。

综上，现役地铁如果安装抗蛇行减振器，不仅能大大提升车辆横向振动的鲁棒性，解决提速带来的横向运动稳定性裕量不足问题，而且还让车辆异常出现的一次蛇行运动演变为二次蛇行运动。因此，安装抗蛇行减振器是作为实现服役条件下的地铁车辆提速的一种有效措施。

5 结 论

(1) 服役条件下地铁车辆的车轮半径会随运营里程的增加而减小，导致车辆临界速度降低且横向振动幅值增大，将降低车辆的横向运动稳定性，影响行车安全。

(2) 等效锥度随运营里程的增加呈上升的趋势，等效锥度的增大不仅会降低临界速度，同时还会加剧蛇行运动，不利于行车安全。服役条件下，一旦地铁提速，即使是小等效锥度条件下，若悬挂参数发生异常匹配将发生一次蛇行现象，可能带来车辆横向运动稳定性裕量不足的问题。因此，在车轮镟修和钢轨打磨等维保过程中，建议严格管理等效锥度，适当控制等效锥度来提升车辆横向运动稳定性。

(3) 现役地铁如果安装抗蛇行减振器，不仅能大大提升车辆横向振动的鲁棒性，解决提速带来的横向运动稳定性裕量不足问题，而且还能避免地铁车辆在异常参数匹配下发生一次蛇行运动。因此，面对服役条件下可能出现的横向失稳问题，建议安装抗蛇行减振器，以满足现役地铁车辆提速的需求。