负泊松比内凹蜂窝结构梯度设计与动态冲击响应

张晓楠， 晏石林， 欧元勋， 文 聘

(1.武汉理工大学 新材料力学理论与应用湖北省重点实验室，武汉 430070；2.武汉理工大学 理学院，武汉 430070)

负泊松比结构具有较高的剪切模量、断裂韧性、压痕阻力和抗冲击能力，广泛应用于汽车制造、航空航天、武器工业等领域[1-5]。尤其是负泊松比结构的“拉胀效应”使得其能量吸收的能力得到了显著的提升[6-8]。因此，对负泊松比蜂窝结构的动态吸能性能行为研究具有重要的意义[9-11]。

国内外学者对于蜂窝结构材料在压缩和动态冲击下的变形模式和面内动力学响应特性等进行了研究[12-14]。张新春等[15]讨论了胞元扩张角和冲击速度对蜂窝材料面内冲击变形和能量吸收能力的影响，结果表明胞元扩张角的绝对值越大，冲击端的平台应力越大，冲击速度越高，蜂窝结构表现出更强的能量吸收能力。白临奇等[16]给出了箭头型负泊松比蜂窝结构在中低速冲击载荷下的应力应变关系的理论公式，为蜂窝结构的参数选择和优化设计提供了指导。任晨辉等[17]设计了一种同时具有负刚度负泊松比效应的周期性超材料，该材料结构具有抗冲击吸能性且因其不产生塑性变形的特点而可重复使用。黄秀峰等[18]针对四面内凹金字塔型负泊松比点阵夹层结构在有无聚脲涂覆两种情况下的抗冲击性能进行了研究，结果表明，相比未涂覆聚脲模型，涂覆聚脲的负泊松比点阵夹层结构在受冲击后保持完整，芯层仍具有承载能力。魏路路等[19]将三边反手性蜂窝及传统蜂窝相比，不同冲击速度下内凹-反手性蜂窝均呈现出优异的能量吸收性能。马芳武等[20]将梯度负泊松比点阵结构作为填充材料引入吸能盒设计，发现冲击角度和冲击速度对负泊松比结构的耐撞性能影响较大。Xu等[21]提出了一种正弦负泊松比蜂窝结构，研究了正弦负泊松比蜂窝结构在不同冲击速度下的变形模式和面内动力响应，结果表明，正弦负泊松比蜂窝结构相比其他传统的蜂窝结构具有更好的吸能性能。袁敏等[22]通过引入梯度厚度的概念，探讨了梯度厚度对蜂窝结构能量吸收性能的影响规律，结果表明正向梯度能够有效降低蜂窝结构的平台应力。可见，目前国内外学者对负泊松比结构的研究工作已经逐步开展，但研究构型较为单一且关于变截面思想还未在相关文献涉及。

基于此，本文根据负泊松比内凹蜂窝结构的变形机理，在相对密度不变的情况下，减小垂直于冲击方向的厚度，增大沿着冲击方向的厚度，设计出了一种变截面内凹蜂窝结构。基于功能梯度的概念，根据截面变化率β的变化将不同变截面内凹蜂窝结构组合为梯度变截面内凹蜂窝结构，并通过有限元仿真对不同梯度变化、不同冲击速度的力学性能和能量吸收性能进行了研究。

1 结构与仿真建模

1.1 负泊松比内凹蜂窝结构设计

本文根据常规的内凹蜂窝结构，提出了一种负泊松比变截面内凹蜂窝结构(auxetic re-entrant honeycomb structure with variable cross section,VCRH)，如图1所示。两种胞元结构的倾斜胞壁长度l、水平胞壁长度a和胞壁夹角θ的大小保持一致。在本文中，取l=9.24 mm，a=20 mm，θ=120°。传统内凹蜂窝胞元的所有胞壁均具有厚度为t的均匀截面，变截面内凹蜂窝胞元的水平胞壁具有可变截面。变截面内凹蜂窝胞元的水平胞壁两端最大厚度为t1，中心最小厚度为t2。两种整体结构的长度和宽度相同，面外厚度(z方向)取10 mm。

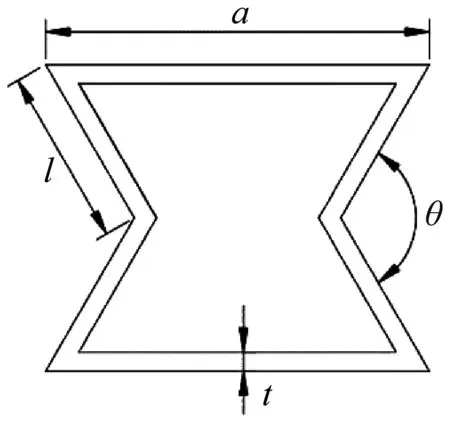
(a) 常规单胞结构图

与密实材料不同，多孔材料还有一个重要的参数，即相对密度，其定义如下

(1)

式中:ρ0为多孔材料表观密度;ρs为基体材料密度。对于具有均匀界面的蜂窝结构，常规内凹蜂窝的相对密度Δρ计算公式如下

(2)

变截面内凹蜂窝结构单胞由两种胞壁组成，包括4个具有均匀截面的倾斜胞壁和2个具有变截面的水平胞壁。变截面内凹蜂窝结构的相对密度可由式(3)给出

(3)

式中，S1和S2分别为倾斜胞壁和水平胞壁的面积

S1=lt

(4)

(5)

为了量化水平胞壁横截面的变化，引入了截面变化率β，其定义为：β=1-t2/t1=(t1-t2)/t1。当β=0时，变截面内凹蜂窝结构退化为常规内凹蜂窝结构。在保持有效密度Δρ不变时，通过选择厚度t1和t2的不同组合，得到了一些具有代表性的形状参数值。所有考虑的蜂窝结构设置,如表1所示。

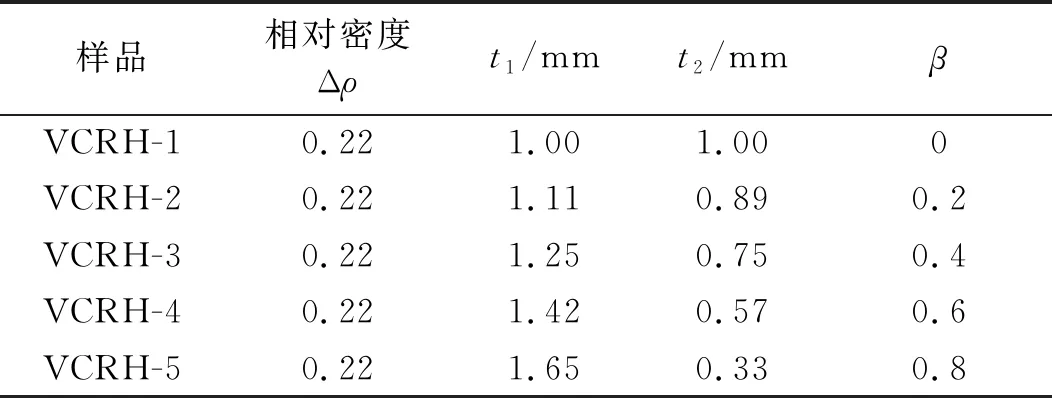
表1 负泊松比变截面内凹蜂窝结构的几何参数

本文根据截面变化率β的变化提出了4种梯度负泊松比变截面内凹蜂窝结构(auxetic re-entrant honeycomb structure with gradient variable cross section,G-VCRH)，如图2所示。图2(a)为正梯度蜂窝结构(G-VCRH-1)，截面变化率β从上向下依次为0.8,0.6,0.4,0.2,0；图2(b)为负梯度蜂窝结构(G-VCRH-2)，截面变化率β从上向下依次为0,0.2,0.4,0.6,0.8；图2(c)为双向正梯度蜂窝结构(G-VCRH-3)，截面变化率β从上向下依次为0.8,0.4,0,0.4,0.8；图2(d)为双向正梯度蜂窝结构(G-VCRH-4)，截面变化率β从上向下依次为0,0.4,0.8,0.4,0。

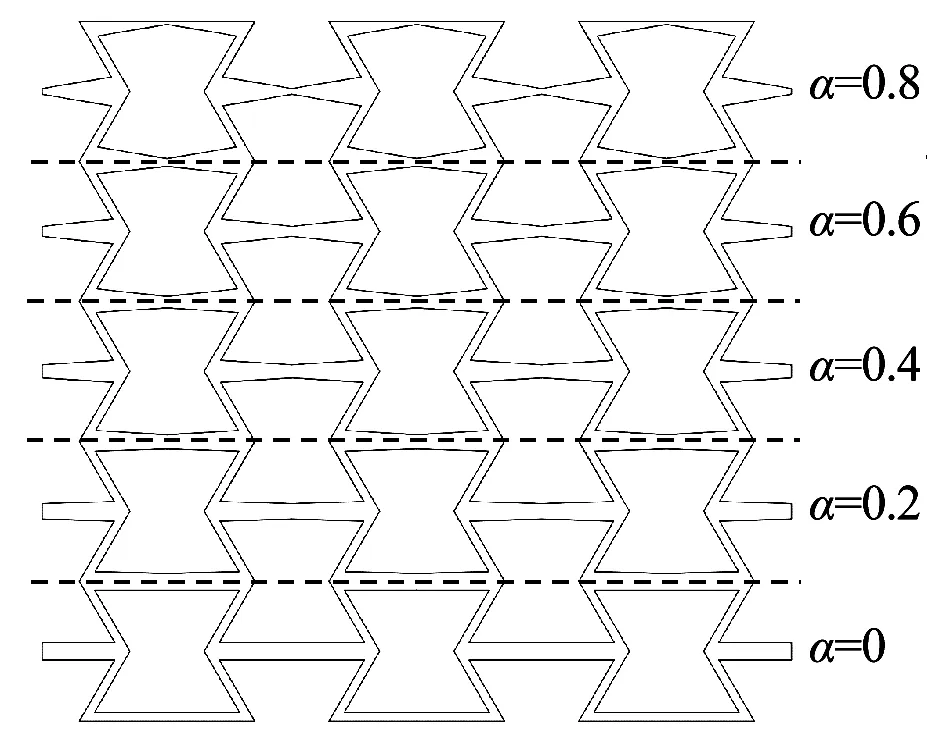
(a) G-VCRH-1

1.2 材料参数及计算设置

本文通过FDM 3D打印技术制造了标准试件，并对标准试件进行密度测量和拉伸实验来获取打印材料的密度、弹性模量、泊松比和屈服强度,如表2所示。

表2 内凹变截面蜂窝结构基体材料参数

在有限元软件ABAQUS中建立的VCRH模型,如图3所示。将蜂窝结构置于两个离散刚板内，并约束底端6个自由度，上刚性板在竖直受到恒定冲击荷载的挤压。为保证计算过程的稳定性和准确性，在内凹蜂窝结构和两个刚性板之间设置了面-面接触，摩擦因数设置为0.3。计算网格尺寸为0.5 mm。为充分计算不同载荷速率下结构的动力学响应，本文设置的载荷速率范围有准静态压缩(5 mm/min)、低速(5 m/s,10 m/s)、中速(20 m/s,30 m/s,40 m/s,50 m/s)。

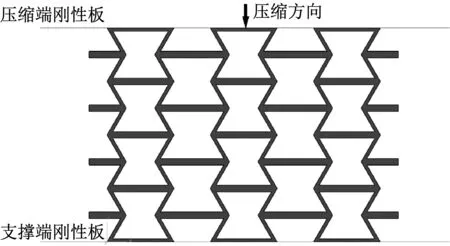
图3 变截面内凹蜂窝结构的准静态压缩有限元模型

2 结果与讨论

2.1 实验与仿真验证

传统内凹蜂窝模型(VCRH)在准静态压缩下的变形模式,如图4所示。 VCRH在受到准静态压缩的初始阶段(ε=0.1)，靠近支撑端的四自由边角处的胞元首先发生明显的凹陷，而下面3层没有明显的凹陷。随着压缩的进行(ε=0.3)，在结构模型4个边角的对角线上形成两条交叉的“X”型的剪切带，在剪切带上胞元被剪切变形。随着压缩的继续进行(ε=0.5)，中间两层的胞元完全溃缩，模型最上端和最下端的胞元也发生了不同程度的变形，“X”型的压密带消失。最终，整个结构溃缩，进入密实阶段。经对比可以发现有限元仿真的变形结果与实验结果具有一致的趋势。

(a) 实验

变截面内凹蜂窝结构在准静态压缩下应力应变曲线实验与仿真的结果基本吻合，如图5所示，两者最大误差绝对值不超过5%，在工程上可以接受。VCRH在受到准静态压缩的初始阶段(ε=0.1)，结构进入弹性阶段，名义应力随应变大体上呈线性增加；随着压缩的进行，结构进入屈服阶段，名义应力在一定幅度内保持稳定；随着压缩的进一步进行，结构被完全压溃后进入密实化阶段，名义应力急剧增加。仿真与实验结果的吻合说明有限元模拟的方法适用于内凹蜂窝模型吸能特性的研究。以下将以有限元仿真结果为基础，对多种梯度变截面内凹蜂窝结构的冲击性能以及吸能机理进行进一步探讨。

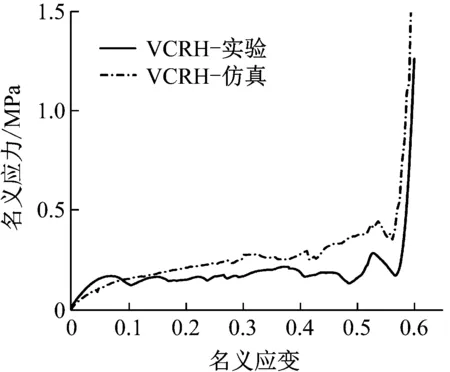
图5 准静态压缩作用下变截面内凹蜂窝结构实验与仿真的名义应力应变曲线

2.2 冲击模式下应力-应变曲线

梯度变截面内凹蜂窝结构在不同冲击速度下动力响应曲线的仿真结果,如图6所示。由图6可知:梯度变截面内凹蜂窝结构的动力学性能规律与传统内凹蜂窝结构基本保持一致，即当冲击刚开始时结构整体处于弹性阶段，名义应力随应变增大而线性增大；随后结构进入屈服阶段，而应力应变曲线进入平台阶段，名义应力出现波动，这可能是由于结构局部发生失效导致；最后结构被完全压溃后进入密实化阶段，名义应力迅速增加。

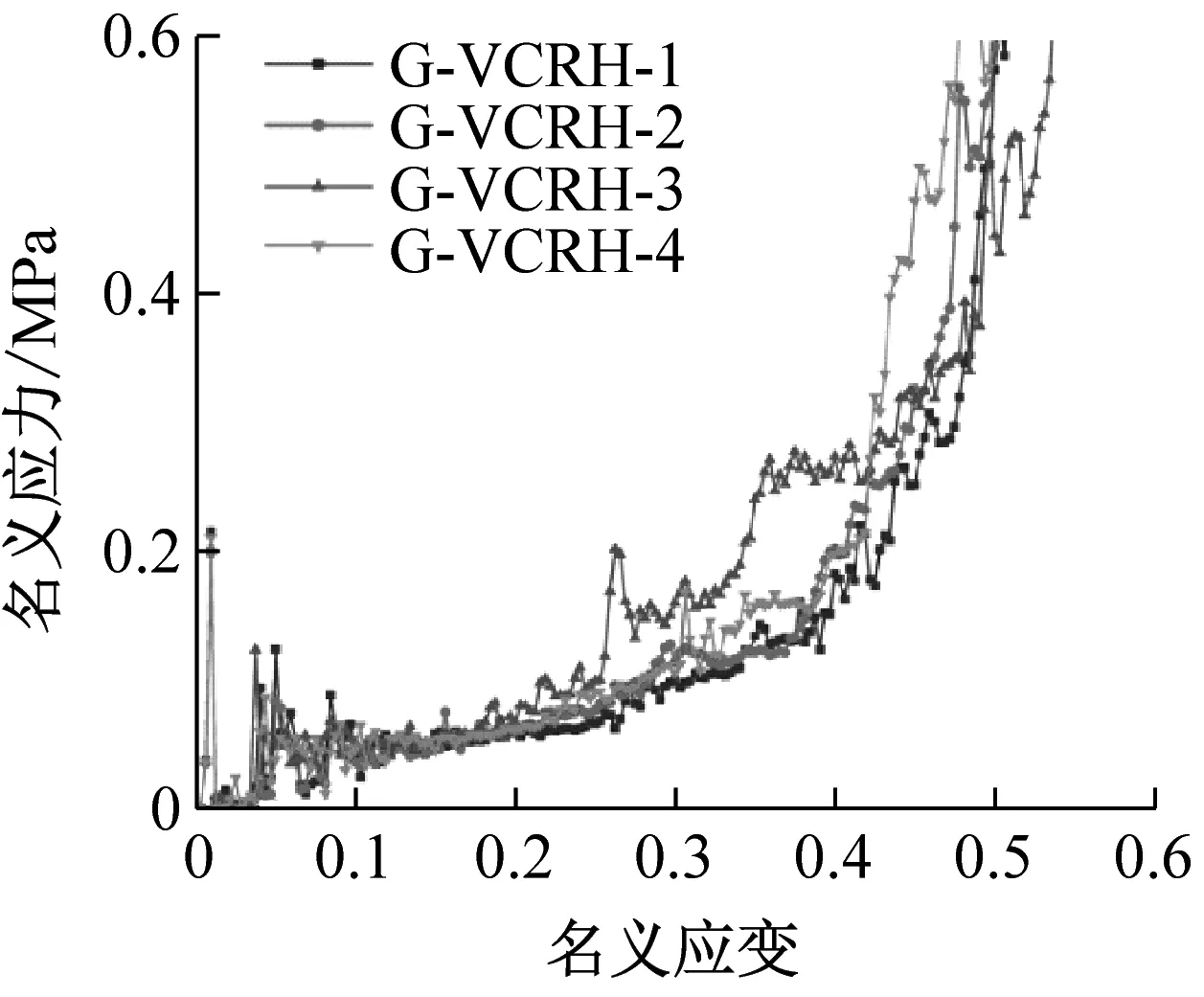
(a) v=5 m/s

2.3 密实应变分析

不同冲击速度下4种结构完全压溃时的应变,如图7所示。由图7可知，对于梯度变截面内凹蜂窝结构，冲击速度与密实应变呈负相关，即冲击速度越大，密实应变值越小。当冲击速度相同时，4种结构的密实应变从小到大排列依次为G-VCRH-3、G-VCRH-1、G-VCRH-2、G-VCRH-4。其中，G-VCRH-1、G-VCRH-2基本一致，且4种结构的密实应变接近结构内部胞元密实应变的平均值，这表明梯度方向对于密实应变没有影响，而密实应变主要受结构内部胞元的影响。

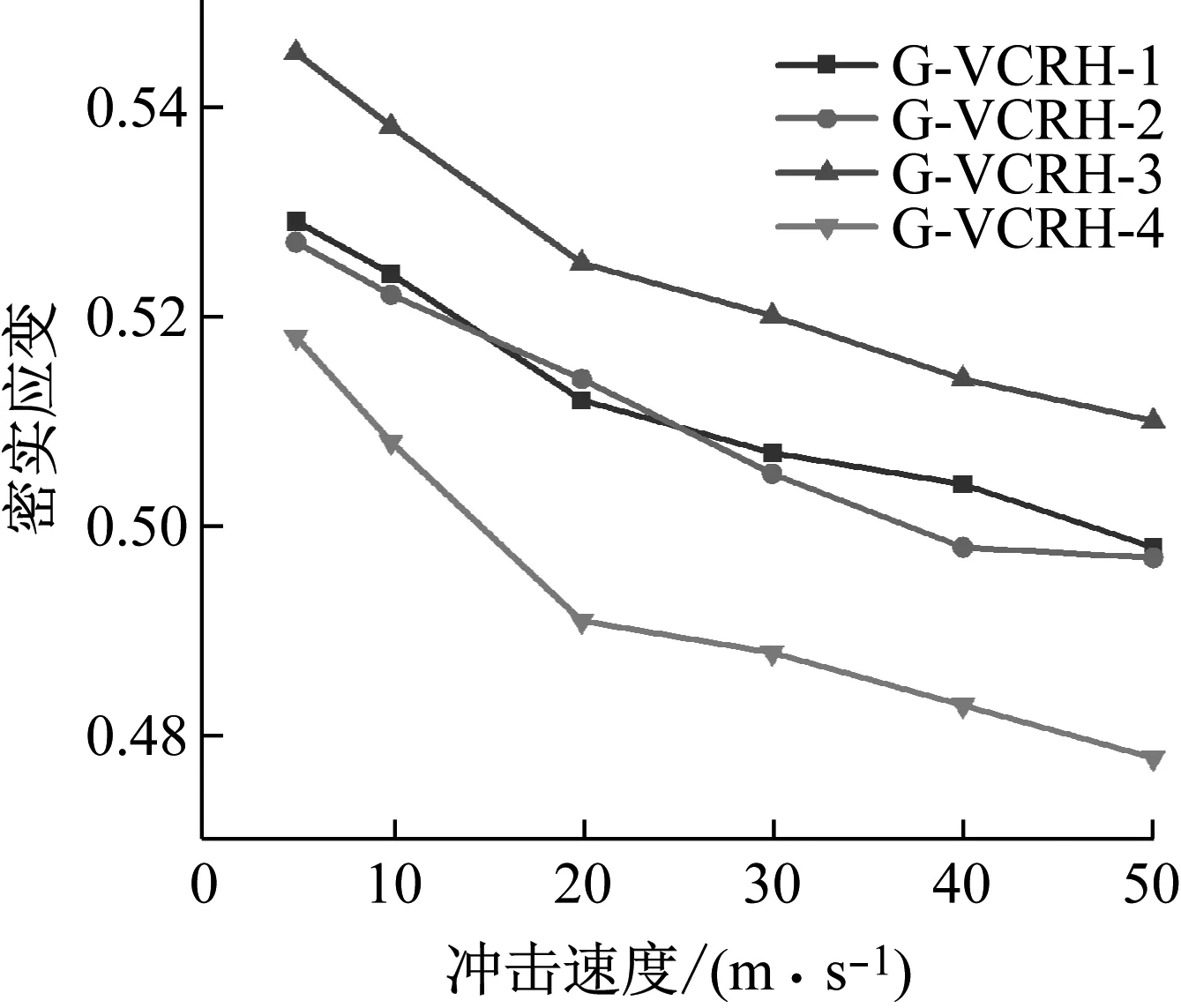
图7 不同冲击速度下梯度负泊松比内凹蜂窝结构的密实应变

2.4 动态平台应力

平台应力(σm)是评价多孔结构吸能能力的一个重要指标。多孔结构的平台应力可以表示为

(6)

式中:σ(ε)为随应变而变化的名义应力；εy为屈服应变，即初始应力峰值所对应的名义应变；εd为密实应变，是材料被压缩密实前的最大应变值。

本小节研究了冲击速度对梯度变截面内凹蜂窝结构冲击端动态平台应力σm的影响。4种梯度变截面内凹蜂窝结构的平台应力。随着冲击速度的增加，平台应力呈现出一个先上升后下降最后再上升的趋势。在(5 m/s,10 m/s)冲击作用下，梯度变截面内凹蜂窝结构G-VCRH-1、G-VCRH-2、G-VCRH-4的平台应力基本相等，均小于G-VCRH-3。在(20 m/s,30 m/s,40 m/s,50 m/s)冲击作用下，梯度内凹蜂窝结构的平台应力从大到小依次为：G-VCRH-3、G-VCRH-4、 G-VCRH-1、 G-VCRH-2。

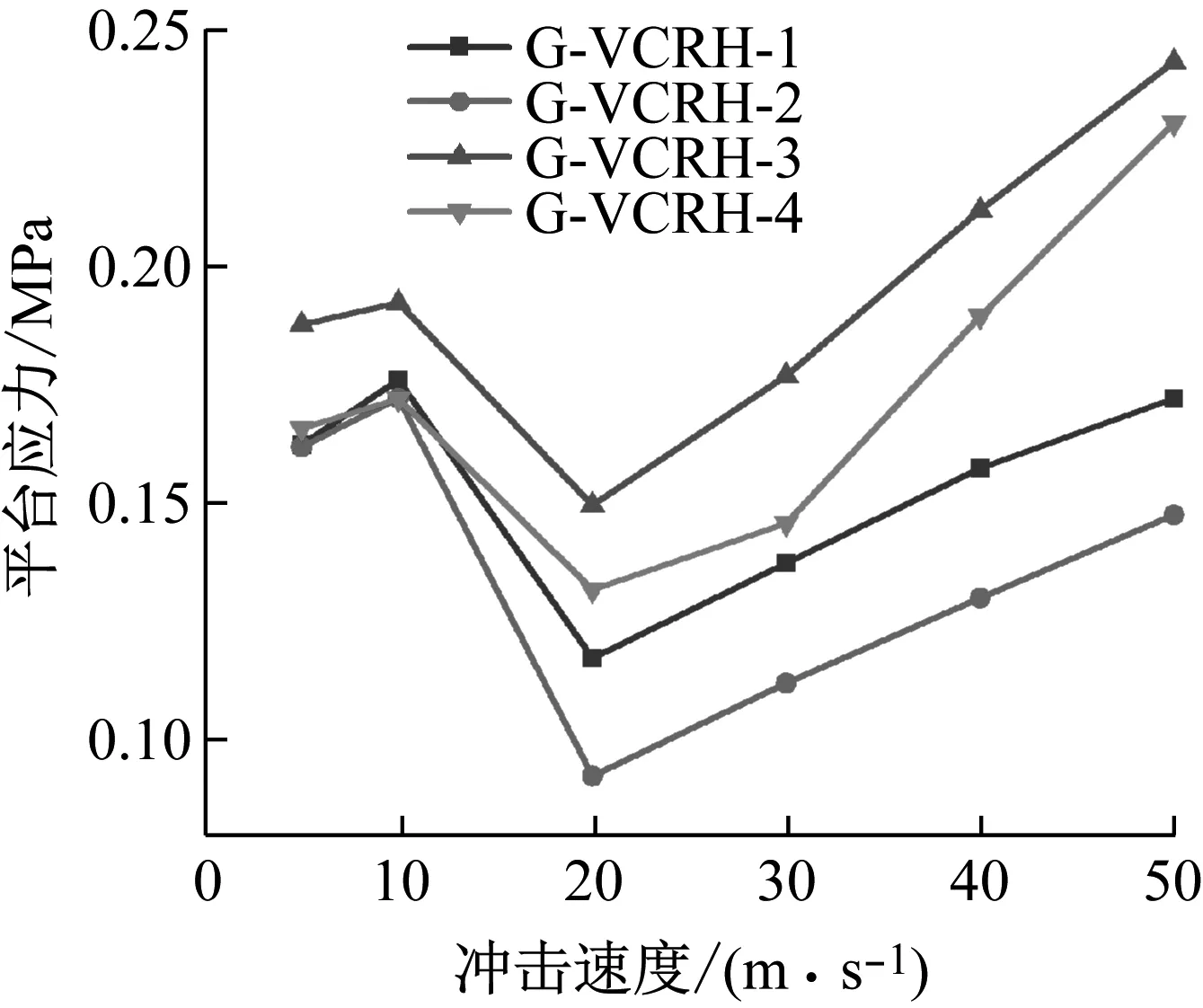
图8 不同冲击速度下梯度负泊松比变截面内凹蜂窝结构的平台应力

2.5 冲击载荷均匀性

为了表征不同几何参数的变截面内凹蜂窝结构的冲击载荷均匀性，冲击载荷效率EIL可以表示为[23]

(7)

式中,σm和σmax分别为动态应力-应变曲线对应的平台应力和最大峰值应力。

蜂窝结构在作为耗能元件中使用时，应保持良好的冲击载荷均匀性。不同冲击速度下梯度变截面内凹蜂窝结构的冲击载荷效率,如图9所示。结果表明，随着冲击速度的增大，梯度负泊松比内凹蜂窝结构呈现先下降，后缓慢上升的趋势。在低速冲击时，其结构的冲击载荷效率最大。在一个恒定的冲击速度下，梯度负泊松比内凹蜂窝结构的冲击载荷效率从大到小为：G-VCRH-3、G-VCRH-4、 G-VCRH-1 、G-VCRH-2。

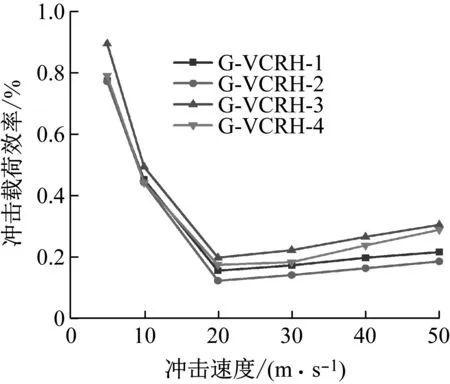
图9 不同冲击速度下梯度负泊松比变截面内凹蜂窝结构的冲击载荷效率

2.6 能量吸收特性

比吸能ASE是评价多孔材料吸能能力的一个关键指标，其定义为总能量吸收量与质量之比，公式如下

(8)

式中:m为试样的质量;V和ρ0分别为相应的体积和密度。

不同冲击速度下梯度变截面内凹蜂窝结构的比吸能,如图10所示。结果表明，随着冲击速度的增加，比能量吸收呈现出一个先下降后上升的趋势。在(5 m/s)冲击时，结构的能量吸收性能最好。且梯度变截面内凹蜂窝结构G-VCRH-1、G-VCRH-2、G-VCRH-4的比能量吸收基本相等，均小于G-VCRH-3。在(10 m/s,20 m/s,30 m/s,40 m/s,50 m/s)冲击作用下，梯度内凹蜂窝结构的比能量吸收从大到小依次为：G-VCRH-3、G-VCRH-1、 G-VCRH-2、 G-VCRH-4。

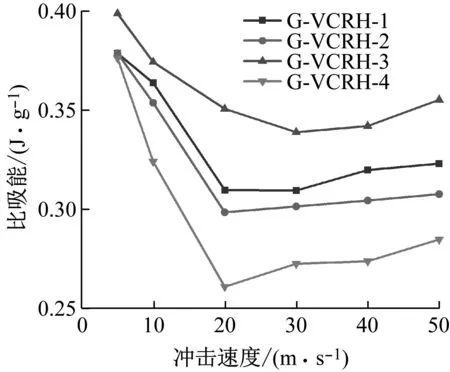
图10 不同冲击速度下梯度负泊松比内凹蜂窝结构的比能量吸收

3 结 论

本文针对内凹蜂窝结构的变形机理，设计出一种变截面内凹蜂窝结构，并在准静态压缩作用下将结构进行有限元仿真和实验验证，结果表明，有限元仿真结果和实验吻合良好。

基于功能梯度的概念，将不同变截面内凹蜂窝结构组合为4种梯度变截面内凹蜂窝结构：正梯度蜂窝结构、负梯度蜂窝结构、双向正梯度蜂窝结构、双向负梯度蜂窝结构；并进行了不同冲击速度下的有限元模拟。结果表明，在低速冲击作用时，结构的能量吸收性能最好，随着冲击的增加，能量吸收性能大体上呈现出先减少后增加的趋势。在某一特定的冲击速度下，双向负梯度的能量吸收效果优于其他3种梯度结构。