高聚物胶凝戈壁土的动模量及阻尼比试验研究

杨海华， 刘 亮， 刘汉龙,4， 高鹏展， 陈育民

(1. 新疆农业大学 水利与土木工程学院， 乌鲁木齐 830052；2. 河海大学 岩土力学与堤坝工程教育部重点实验室， 南京 210098；3. 河海大学 土木与交通学院， 南京 210098； 4. 重庆大学 土木工程学院， 重庆 400045)

戈壁土是分布于我国西北干旱地区的一种粗颗粒土，常被作为建筑材料用于大坝填筑、铁路路基或建筑地基等[1]。我国西部处于欧亚地震带边缘，常受到严重的地震灾害影响，主要表现为地基强度破坏、沉降变形或液化等[2]。近年来，学者们对粗粒土的静、动力特性开展了大量的研究，并提出土体的加固技术，对天然土工程性质的某方面不足进行加固处理，改善土的工程性质。加固材料常采用非胶凝类或胶凝类两类，如水泥、粉煤灰、聚合物纤维、玻璃纤维、钢纤维等，能有效提高土的抗剪强度、改善变形能力、抗液化能力等[3-4]。随着现代工业的发展，人们还采用多元异氰酸酯、多元羟基化合物等原料合成的高分子聚合物材料进行土体加固，该类材料具有强度高、延伸率大、回弹性好、粘接性能优等特点，被广泛应用到多个领域[5]。对于戈壁土强度较高而黏聚力低，在地震灾害中常出现变形较大、地基液化等问题[6]。如对戈壁土掺入黏弹性较好的高聚物改善其工程性质，将对西北地区的工程建设起到积极的推动作用。

对于土体加固处理，Schlosser等[7]于1974年首先进行了加筋土的力学性质试验，之后学者们开始重视加固土体的静、动力特性，从而开展了大量的研究工作。Maher等[8]通过共振柱、扭剪试验研究了纤维加固砂土的动模量和阻尼比，认为加固效果与剪应变幅、围压、振次、纤维含量、长细比等因素有关，纤维加固对砂土的动模量影响较大，对阻尼比影响较小。Li等[9]进行了纤维加固土的动模量试验，分析了纤维含量、围压、循环次数等对弹性剪切模量的影响，并建立了纤维加固土的非线性弹性本构模型。杨贵[10]进行了土工格栅加固筑坝料的动三轴试验，研究了围压、孔隙比、加筋层数和加筋间距对加固堆石料的动模量和阻尼比的影响。Shewbridge等[11]进行了钢丝加固砂土的大型空心扭剪试验，研究钢丝加固土的动力特性，结果表明在0～10 Hz内，荷载频率对未加固土、加固土的动模量无影响；在应变小于5%时钢丝加固砂土的动模量无明显影响，当应变大于7%时，钢丝加固抑制了砂土螺旋剪切破坏面的形成。Chauhan等[12]进行了粉煤灰和纤维加固粉质砂土的循环三轴试验，得出粉煤灰和纤维加固可提高土的回弹模量、减小残余变形的结论，加固土的残余变形与循环次数、偏应力、围压等因素有关。刘汉龙等[13]研究了围压、循环荷载条件和加筋间距对土工格栅加筋堆石料动残余变形的影响，结果表明加筋后堆石料的动残余变形明显减小，可通过扩大加筋范围、减小加筋间距、提高筋材的刚度和强度来减小土石坝在地震作用下的永久变形。傅华等[14]研究了水泥胶凝砂砾石料的动力特性，得出水泥的胶凝作用可提高砂砾石的动剪切模量，降低围压对动剪切模量和动残余变形的影响，并且水泥胶凝砂砾石料的动残余变形规律仍可采用沈珠江残余变形模型描述。庄海洋等[15]利用橡胶颗粒与砂混合，进行了动三轴试验，得出橡胶颗粒含量与橡胶颗粒-砂混合料破坏振次的关系。李雪菊等[16]研究了荷载分级对砂-锯末混合模型土动剪切模量和阻尼比的影响，认为随荷载的增大，滞回圈面积和形状也随之改变。

以上研究以土工格栅、纤维、水泥等作为加固材料，研究了土体加固后的动力特性，得到了较为丰硕的成果，但对于加固戈壁土的研究较少。鉴于此，本文选用高聚物(双组份弹性聚氨酯)掺入戈壁土中，形成高聚物胶凝戈壁土，在同一密度下进行中型动三轴试验，研究高聚物质量比、围压、固结比等因素对高聚物胶凝戈壁土的动弹性模量和阻尼比的影响，对比分析不同高聚物质量比下滞回曲线的变化规律，并建立适用于高聚物胶凝戈壁土的沈珠江修正模型。本文对戈壁土的加固提出了一种新方法，并可为高聚物胶凝戈壁土的工程应用提供理论依据。

1 动三轴试验

1.1 试验设备和材料

试验设备采用新疆水利工程安全与水灾害防治重点实验室的大型多功能动静三轴试验机。该试验机可进行直径为Φ300 mm和Φ150 mm两种尺寸的静、动力三轴试验；轴力、围压加载系统采用液压伺服作动器，可实现轴向、径向(围压)不同动应力、不同相位差的单、双向循环加载试验；动荷载加载频率f为0.01～10.00 Hz。

试验用戈壁土料取自新疆和田地区某水利枢纽工程现场。考虑本次试验为直径Φ=150 mm的中型三轴试验，按照相关规范要求，对戈壁土粒径超过40 mm的颗粒进行剔除，处理后戈壁土料的颗粒级配曲线如图1所示。试料不均匀系数Cu=32.7，曲率系数Cc=1.2，属于级配良好砾，小于0.075 mm颗粒含量为0.7%；经试验测得试料的比重为2.71，最大干密度为2.28 g/cm3，最小干密度为1.85 g/cm3。

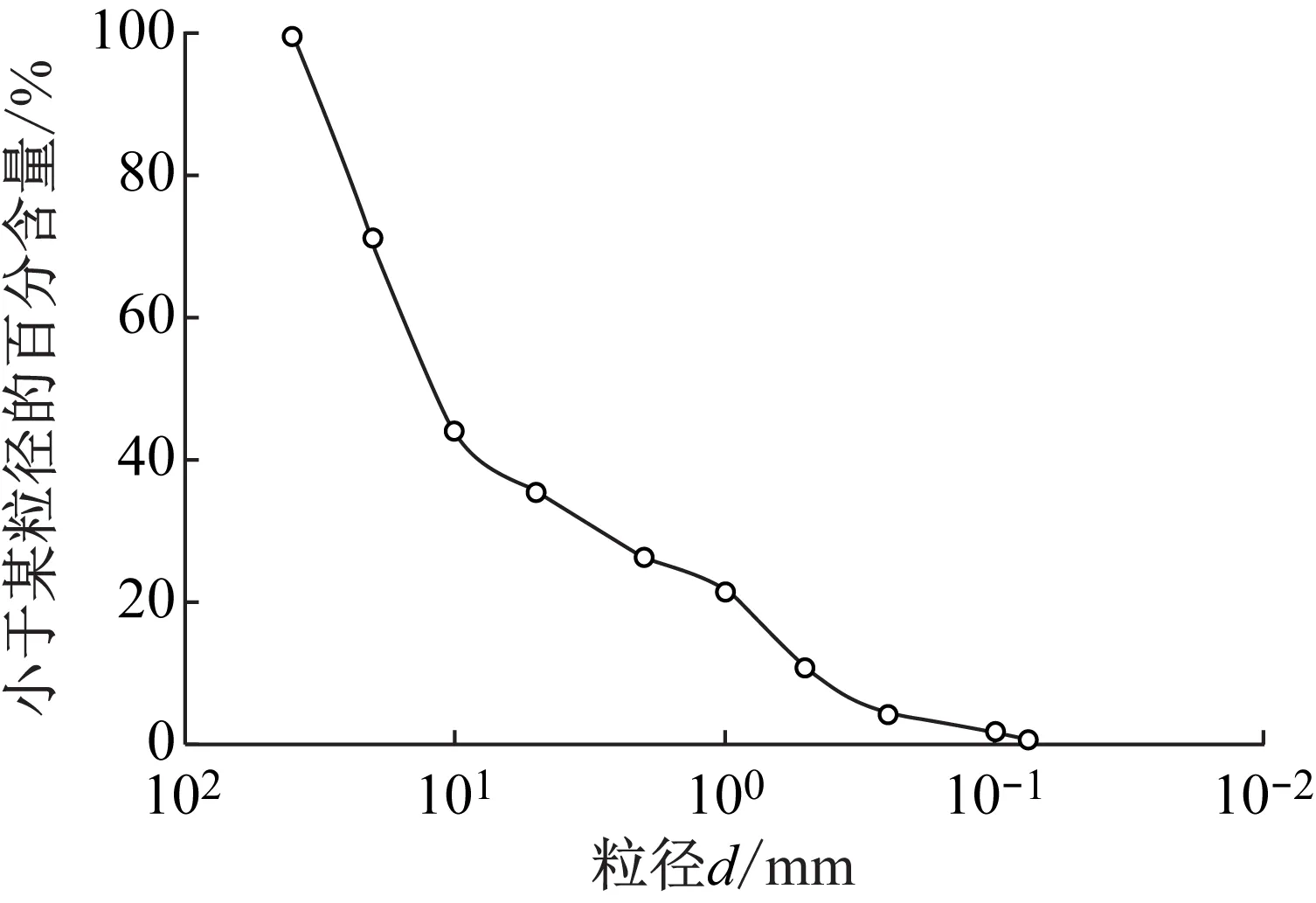
图1 试验戈壁土颗粒级配曲线

本次试验用高聚物为双组份弹性聚氨酯，具有较好的粘接性能和弹性恢复能力，其拉伸强度为2.3 MPa，拉伸伸长率为528%，低温弯折性能可达到-40 ℃，高温在120 ℃时未出现软化现象，其基本性能如表1所示。

表1 双组份弹性聚氨酯基本性能

1.2 试样制备

为研究高聚物掺量对加固后戈壁土的动力特性的影响，采用高聚物质量比Rp(高聚物质量与戈壁土质量的比值)作为衡量指标，进行不同高聚物质量比Rp的动三轴试验。试样成型前，先进行高聚物(双组份弹性聚氨酯)两种原料的混合，拌合均匀后为黑亮色、稠度均匀、流动性好的膏状物；然后按所需质量比称取高聚物和戈壁土进行拌和，形成高聚物戈壁土混合物。为使混合物均匀，将高聚物和戈壁土加入搅拌机中搅拌4 min，搅拌前、后的高聚物戈壁土如图2所示。

(a) 搅拌前

采用击实方法成型试样，将搅拌均匀的高聚物戈壁土装入三轴试模(Φ150 mm×300 mm)中，按密度要求称取混合料，分两层装入进行击实，以击实后试样的高度作为标准控制试样密度。考虑高聚物质量比Rp对高聚物胶凝戈壁土的密度影响，减小试样密度对试验结果的影响，本次试验所有试样密度均取戈壁土的相对密度Dr=0.70(ρd=2.133 g/cm3)。击实后试样在试模中静置24 h，待形成高聚物胶凝戈壁土后脱模，成型后高聚物胶凝戈壁土试样如图3(a)所示。对高聚物质量比Rp为0的试样(天然戈壁土)直接采用中型三轴仪试样成型筒在动三轴仪上击实成型。

1.3 试验方法

在动模量和阻尼比试验中，将高聚物胶凝戈壁土试样装入动三轴仪，如图3(b)所示，安装压力室，对试样进行抽气饱和，使试样饱和度达到Sr≥95%后进行试验。根据试验要求施加不同围压和轴向固结应力进行试样固结，固结完成后保持围压不变施加不同的轴向动应力进行试验。采用一个试样分多级施加动应力进行试验，陆晓炎等[17-18]的研究结果均指出先期振动对材料的应力应变有一定的影响，为减小先期振动对试验结果的影响，每个试样按等差方式施加5级动应力，控制动应力比(cyclic stress ratio，CSR：为一循环周期内最大动应力幅值与围压之比)的最大值不大于0.95；循环加载采用正弦波，每级动应力下进行5次振动，采用第2次～第4次振动的平均值作为试验结果进行处理分析。

(a) 三轴试样

为对比分析各影响因素对高聚物胶凝戈壁土动力特性的影响，进行了不同高聚物质量比Rp、不同围压σ3、不同固结比Kc和不同加载频率f条件下的动模量和阻尼比试验。共完成动三轴试验11组，每组试验3个试样，试验方案如表2所示。

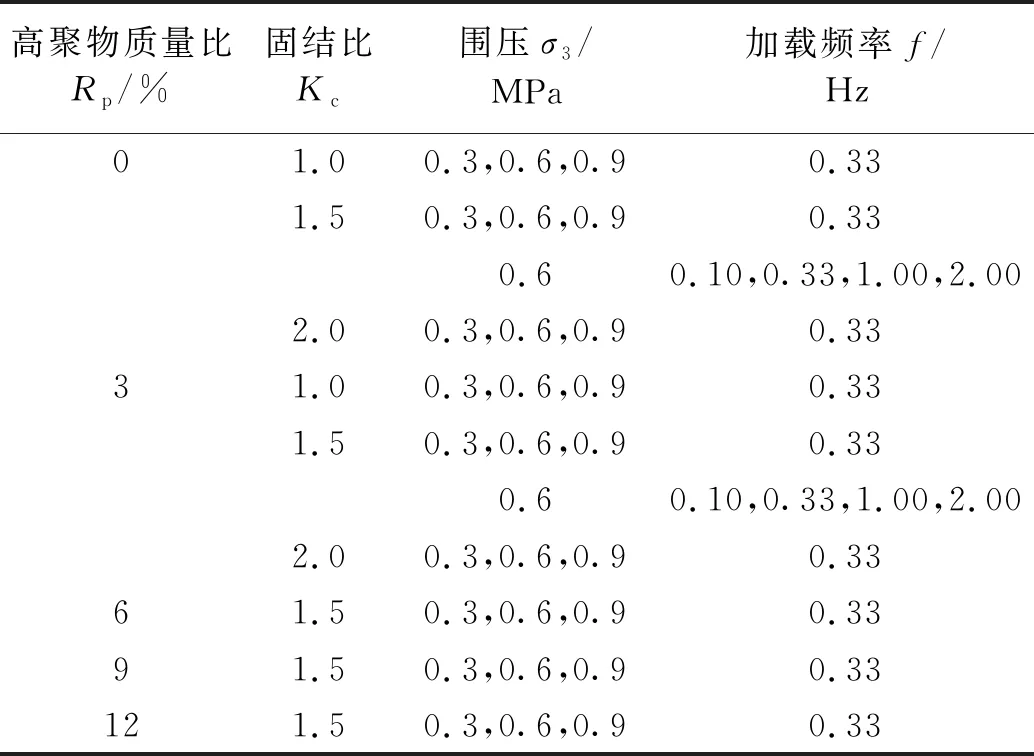
表2 动模量和阻尼比试验方案

2 动模量和阻尼比试验结果

土的动弹性模量(或动剪切模量)和阻尼比是研究土动力特性的两个重要参数[19]，表达式为

(1)

(2)

式中：Ed为动弹性模量，MPa；σd为轴向动应力，MPa；εd为轴向动应变；λ为阻尼比；AL为滞回圈的面积，表示一个周期内的能量损耗；AT为滞回圈上最大动应力与动应变乘积的0.5倍(三角形面积)，即一个周期内加载所储存的总能量。

动弹性模量反映土体在遭受振动荷载作用下应力-应变曲线(骨干曲线)的变化规律；阻尼比表征土体在循环荷载作用下能量的耗散情况。动弹性模量和阻尼比的变化，对土的振动响应和变形均有较大的影响，下面对不同条件下高聚物胶凝戈壁土的动弹性模量和阻尼比变化规律进行分析。

2.1 高聚物质量比的影响

不同高聚物质量比Rp在围压σ3=0.3 MPa、固结比Kc=1.5、加载频率f=0.33条件下的动应变εd与动应力σd、动弹性模量Ed和阻尼比λ的变化曲线，如图4所示。由图4(a)可知：在相同动应力水平下，随着高聚物质量比Rp的增大，动应变εd出现先减小后增大的趋势，骨干曲线呈现出先变陡后逐渐变缓过程；在小应变情况下(εd<0.02%)，高聚物的掺入，增加了戈壁土颗粒之间的黏结作用，使其在小应变阶段的动弹性模量增加；由于高聚物自身具有较高的弹性，掺入戈壁土后使高聚物胶凝戈壁土的弹性增加，在受到较大动应力时其应变受高聚物的影响较大，应变量越增加，高聚物质量比Rp越大，在同一动应力下的应变越大。由图4(b)可知：不同高聚物质量比Rp使动模量在小应变情况下增大，随着应变量的增加，动模量呈逐渐减小的趋势，说明当高聚物质量比Rp较小时可有效提高戈壁土的刚度，Rp增大可提高其适应变形的能力；阻尼比λ随高聚物质量比Rp的增加逐渐减小，但降低幅度较小。

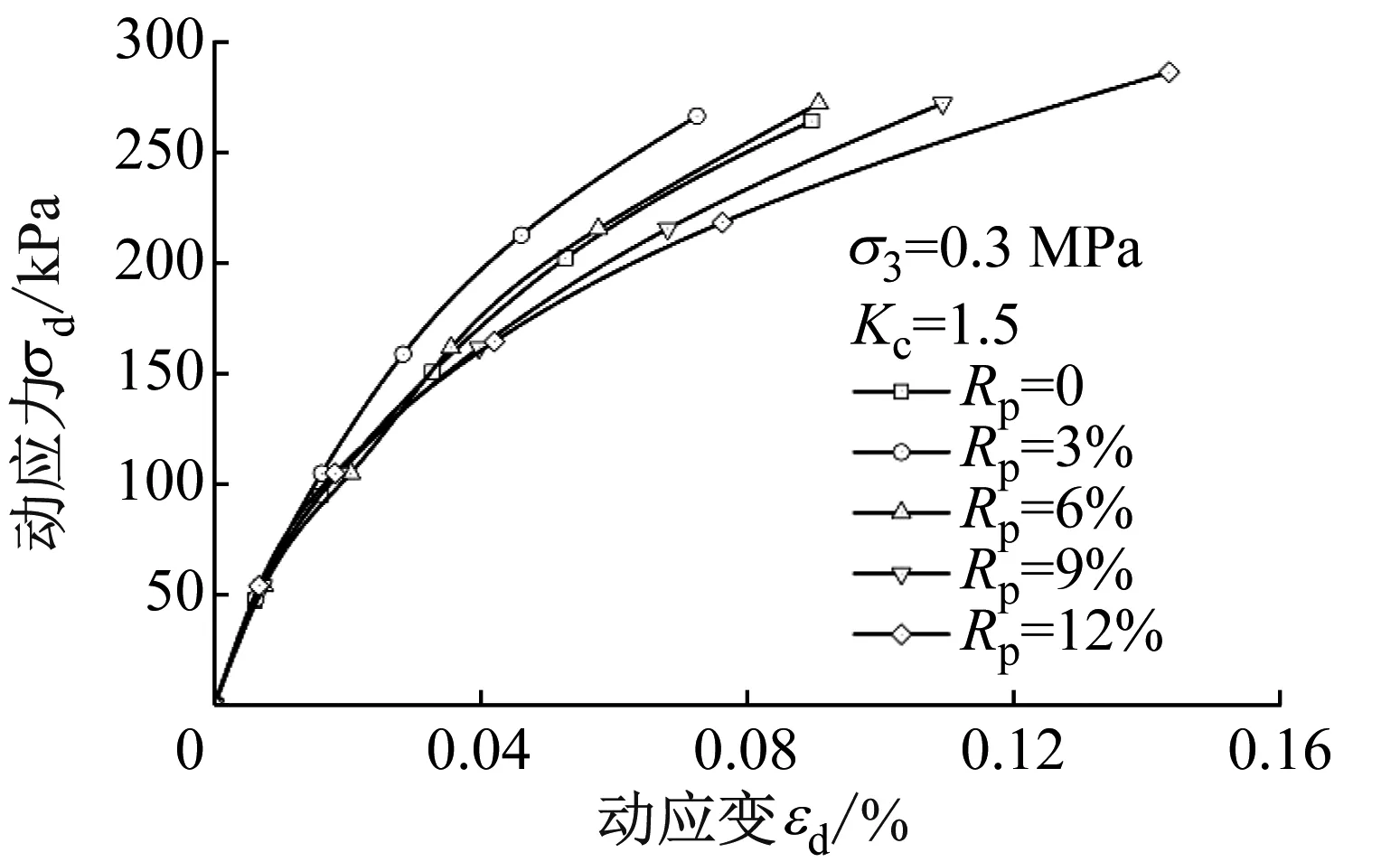
(a) 动应力-动应变曲线

不同动应力比CSR下高聚物胶凝戈壁土的动弹性模量对比，如图5所示。由图5可知：动弹性模量Ed随CSR的增大，逐渐减小；在相同CSR时，高聚物质量比Rp对动弹性模量的影响较大，当CSR为0.157时，随Rp的增大，动弹性模量逐渐增大；而当CSR>0.157后，动弹性模量随高聚物质量比的增加呈先增大后减小趋势，在Rp为3%时出现最大值。试验结果与Shewbridge等、邱成春等[20]通过钢丝加固、水平-竖向加固土体的动力试验得到的加固提高土的动弹性模量，降低了阻尼比的结论存在一定差异。这主要是由于加固材料的性质不同而造成的，钢丝加固和水平-竖向加固主要提高了土体的整体性，土体在受力时由于土颗粒受加固材料束缚作用而很难出现相对位移，从而提高了土体的刚度，模量增大。而高聚物为高弹性聚合物加固材料，有较高的弹性变形性能，在高聚物质量比Rp较低时，高聚物在土颗粒表面形成一层薄膜，使颗粒之间有效的粘接在一起，此时孔隙中无多余的高聚物，呈现出整体性提高，模量增大；随着Rp的增加，土颗粒间的高聚物厚度增大，土体内部孔隙被高聚物填充，土体颗粒排列形态出现部分颗粒悬浮在高聚物中的现象，在受动荷载作用时土体和高聚物共同承担作用力，高聚物受力后出现较大弹性变形，表现出在相同CSR时Rp越大应变越大、动弹性模量降低的现象。

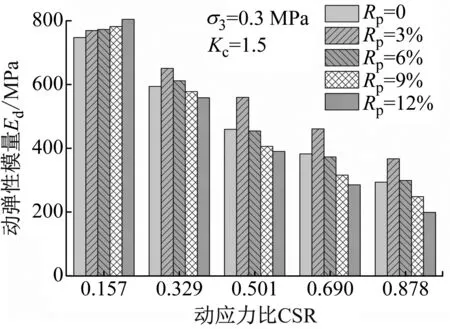
图5 CSR对高聚物胶凝戈壁土动模量的影响

在动荷载作用下，土的动变形分为残余变形和弹性变形。其中，残余变形在动荷载作用过程中稳定增长，具有不可恢复和单调增长特性。在动应力比CSR为0.329时高聚物胶凝戈壁土5次循环荷载作用过程中的动应变时程曲线，如图6所示。由图6可知，Rp为0的天然戈壁土经5次循环荷载后的残余动应变较大，为0.141%；而Rp>0的高聚物胶凝戈壁土残余动应变较小，且Rp越大，残余动应变越小，经过5次循环荷载后的残余动应变最大值为0.026%，其残余动应变为天然戈壁土的18.4%，说明高聚物的掺入，能有效降低动荷载作用下戈壁土的残余变形。其原因在于Rp为0的天然戈壁土在循环荷载作用下，加载使土体颗粒发生相对移动而产生弹塑性变形，卸载时只有弹性变形部分恢复，所以出现随振次的增加残余动应变逐渐增大；而对于Rp>0的高聚物胶凝戈壁土，一方面高聚物的粘接作用使戈壁土颗粒紧密黏结成一个整体，阻碍了加载时土粒的相对移动，塑性变形较小；另一方面，土体内部孔隙填充的高聚物具有高弹性，在受力时仅发生弹性变形，在卸载阶段高聚物又恢复到初始状态，表现出高聚物加固后的戈壁土残余变形减小的特性。并且在受振动荷载时，高聚物能有效减弱动荷载的冲击作用，使土体受到的作用力相对减小，从而降低动荷载对戈壁土的破坏作用。

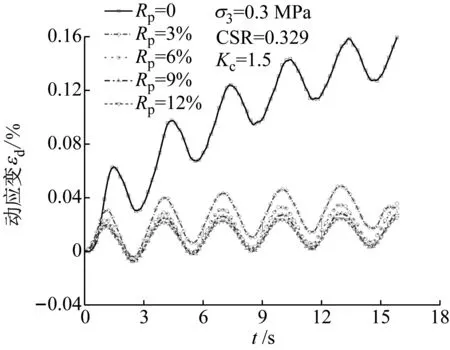
图6 不同高聚物质量比Rp下动应变时程曲线

2.2 围压的影响

不同围压σ3在高聚物质量比Rp=0和Rp=3%、固结比Kc=1.5、加载频率f=0.33条件下的动应变εd与动应力σd、动弹性模量Ed和阻尼比λ的变化曲线，如图7所示。由图7(a)可知，各级围压下的骨干曲线服从双曲线规律，可用双曲线对骨干曲线进行拟合。随着围压σ3的增大，骨干曲线的斜率增大。主要是因为在围压增长时土体内部球应力增大，土粒发生挤密效应，在受动应力σd作用时其本身的模量提高了。由图7(b)可知，在相同的高聚物质量比Rp下，围压增加动弹性模量Ed增大，并随着动应变εd的增加而逐渐减小。阻尼比λ随围压的变化不明显，仅随应变的增大而增大，在动应变相同时，围压的增大反而使阻尼比略有降低。

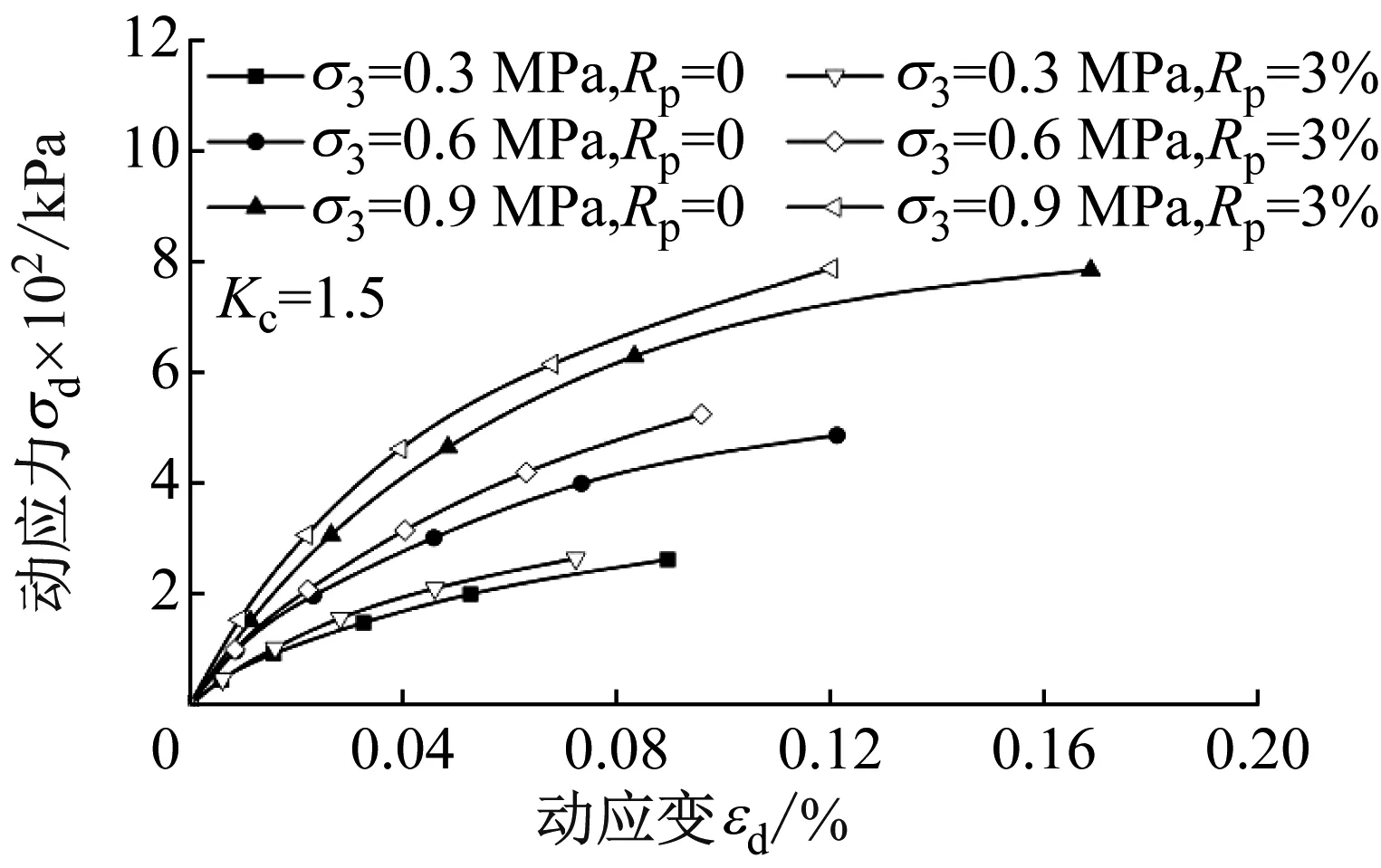
(a) 动应力-动应变曲线

2.3 固结比的影响

不同固结比Kc在高聚物质量比Rp=0和Rp=3%、围压σ3=0.3 MPa、加载频率f=0.33条件下的动应变εd与动应力σd、动弹模量Ed和阻尼比λ的变化曲线，如图8所示。由图8(a)可知，固结比Kc对高聚物胶凝戈壁土的骨干曲线有明显的影响，固结比越大，骨干曲线越陡，斜率增大。由图8(b)可知，在相同的动应变条件下，固结比Kc增大，戈壁土和高聚物胶凝戈壁土的动弹性模量Ed均增大，而戈壁土的阻尼比λ减小，高聚物胶凝戈壁土的阻尼比λ变化较小。袁晓铭等[21]认为固结比的增大，使砂土的有效球应力增加，从而引起动弹性模量的增大,与本次试验的结果一致，说明高聚物胶凝戈壁土材料亦具有相同的性质。

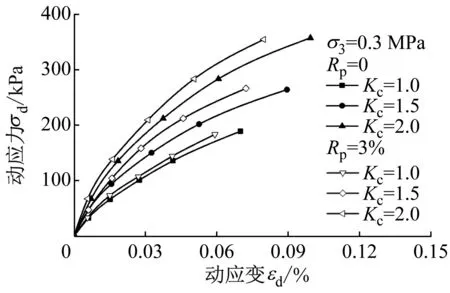
(a) 动应力-动应变曲线

2.4 加载频率的影响

不同加载频率f在高聚物质量比Rp=0和Rp=3%、围压σ3=0.3 MPa、固结比Kc=1.5条件下的动应变εd与动应力σd、动弹模量Ed和阻尼比λ的变化曲线，如图9所示。由图9可知：在相同Rp时，试验的4种加载频率下的骨干曲线几乎重叠，说明加载频率对高聚物胶凝戈壁土骨干曲线的影响较小；并且动弹性模量和阻尼比在不同加载频率下也无明显变化，该结果与郭熙灵[22]得出的振动频率对粗粒土的动弹性模量和阻尼比影响较小的结论是一致的。

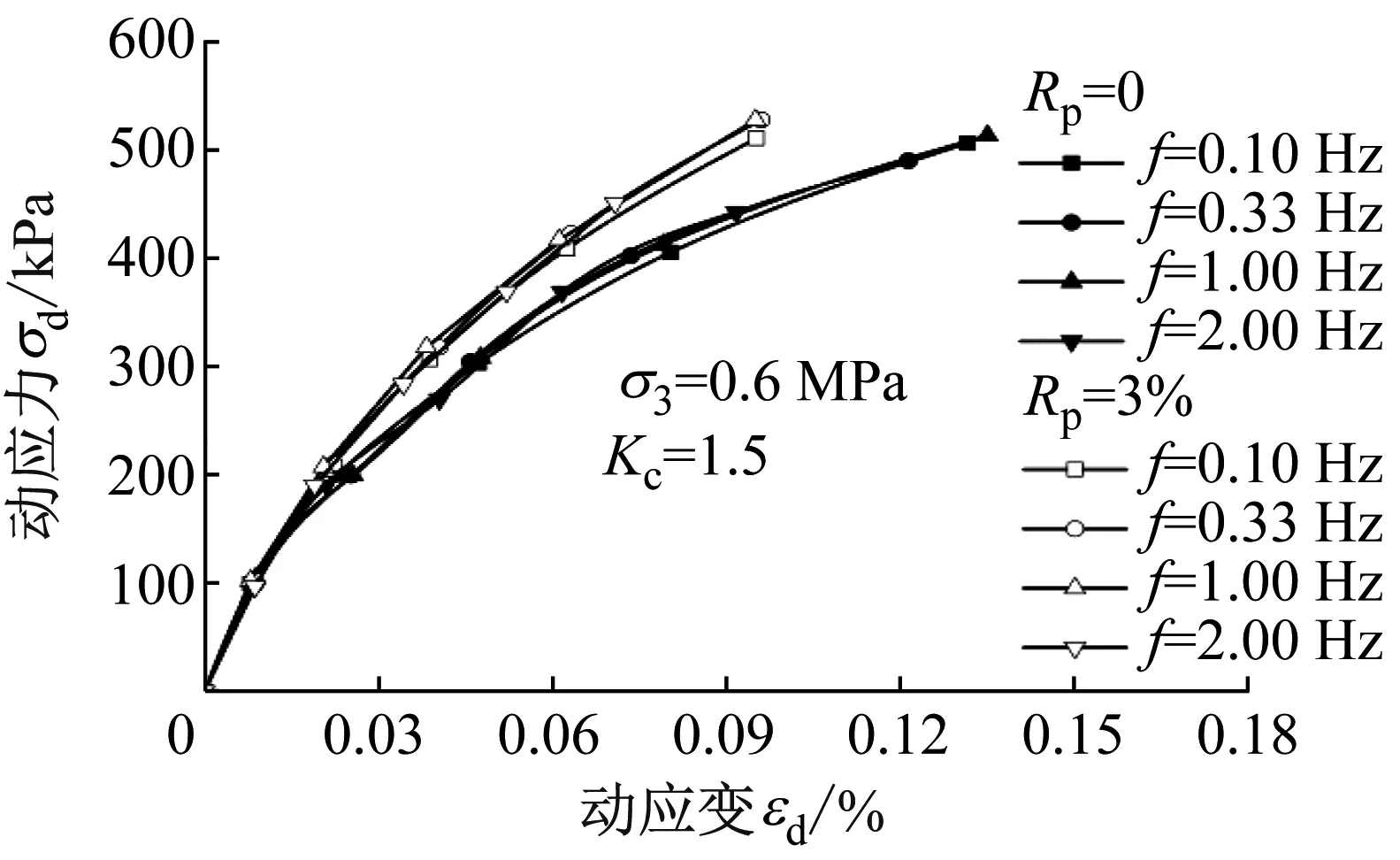
(a) 动应力-动应变曲线

2.5 不同高聚物质量比的滞回曲线分析

滞回曲线可反映高聚物胶凝戈壁土材料在循环荷载作用下的应力-应变关系，同时可以计算出动弹性模量、阻尼比等动力学参数。当动应力比CSR为0.501时，不同Rp下的滞回曲线对比，如图10所示。由图10可知，在相同的动应力σd下，Rp越大，高聚物胶凝戈壁土在周期荷载下产生的应变滞后现象越小，加载、卸载过程的曲线对称性越好，说明掺入高聚物后，戈壁土的弹性增大，变形恢复能力有所提高。Figueroa等[23]提出循环荷载作用下的能量耗散可用滞回圈面积的大小来衡量，图10可以看出当Rp为0时滞回圈的面积最大，说明在一个循环内天然戈壁土吸收的能量最多，破坏的可能性最大，所以高聚物加入戈壁土后减小了循环荷载对高聚物胶凝戈壁土的破坏作用。

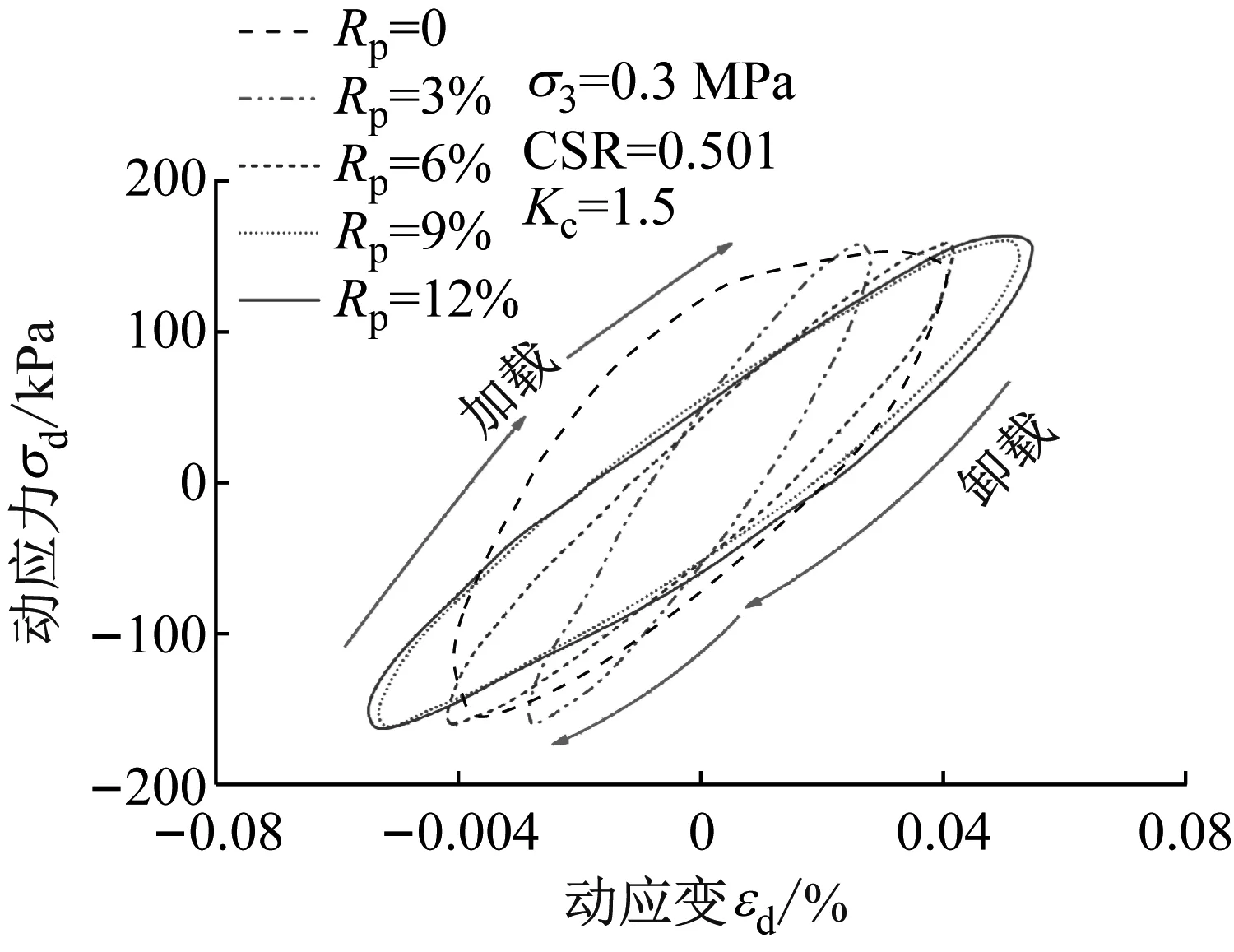
图10 高聚物质量比Rp对滞回曲线的影响

3 本构模型修正

3.1 沈珠江动力模型

目前，关于土的力学性能模型主要有理想弹塑性模型、黏弹性模型、黏塑性模型和双线性模型等。对于土的动力本构模型中，以Hardin等[24]提出的等效线性模型应用最广。该模型中，假定动应力-动应变关系曲线(骨干曲线)符合双曲线变化规律，表达式为

(3)

式中：σd为动应力，MPa；εd为动应变；a，b为试验参数。当εd→∞时，最大动应力σd,max=1/b；εd→0时，求得最大动弹性模量Ed,max=1/a。

沈珠江等[25]认为Ed,max与球应力σm有如下关系

(4)

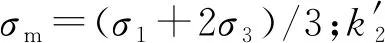
(5)

其中

(6)

(7)

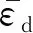
动力分析中一般采用动剪切模量Gd，动剪切模量Gd和动弹性模量Ed有如下关系

(8)

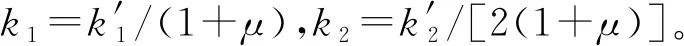
等效阻尼比λ采用式(9)或式(10)计算

(9)

(10)

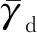
3.2 模型参数确定及修正

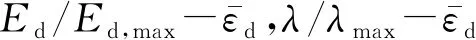
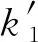
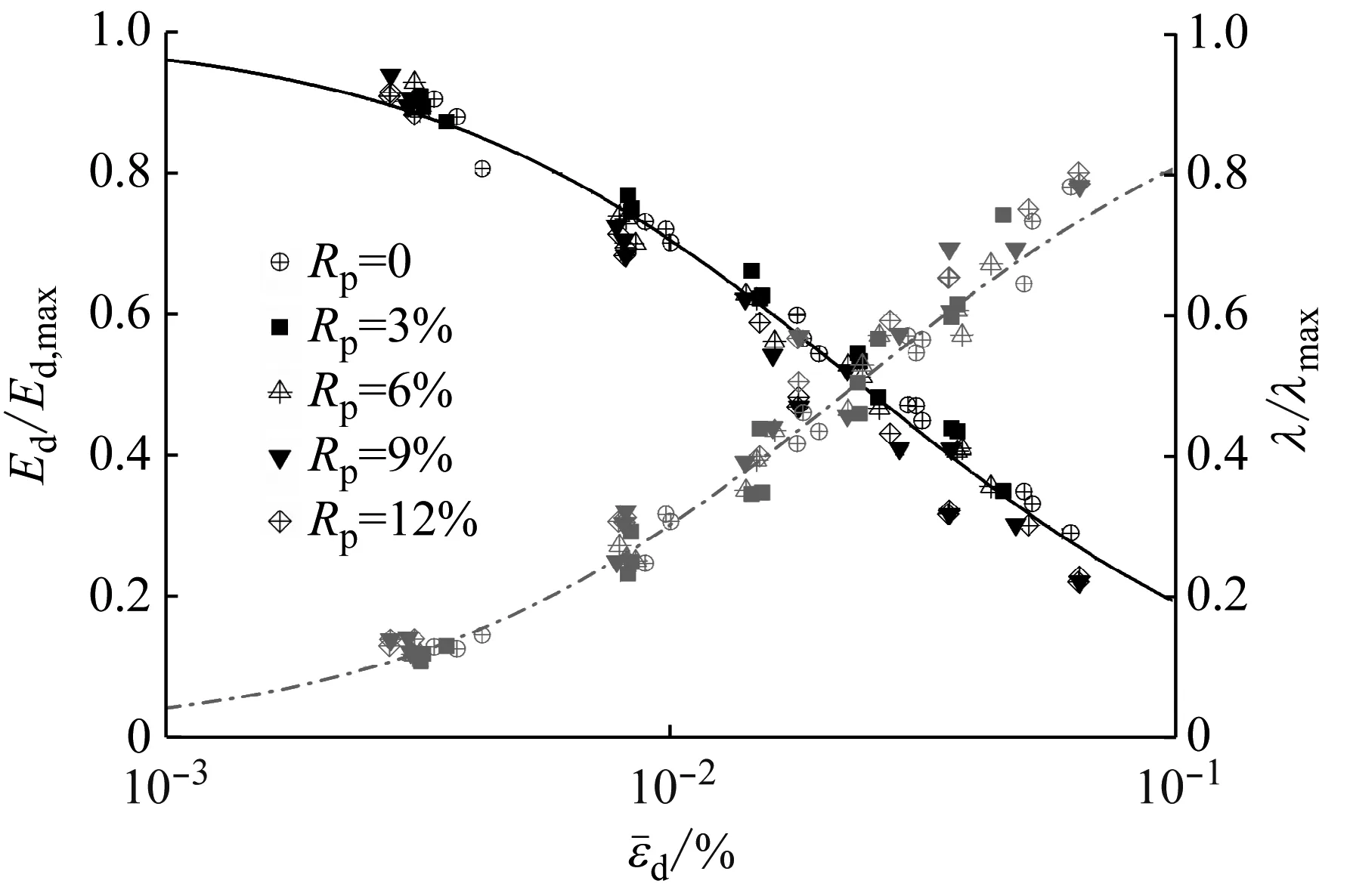
图11 当f=0.33时的曲线

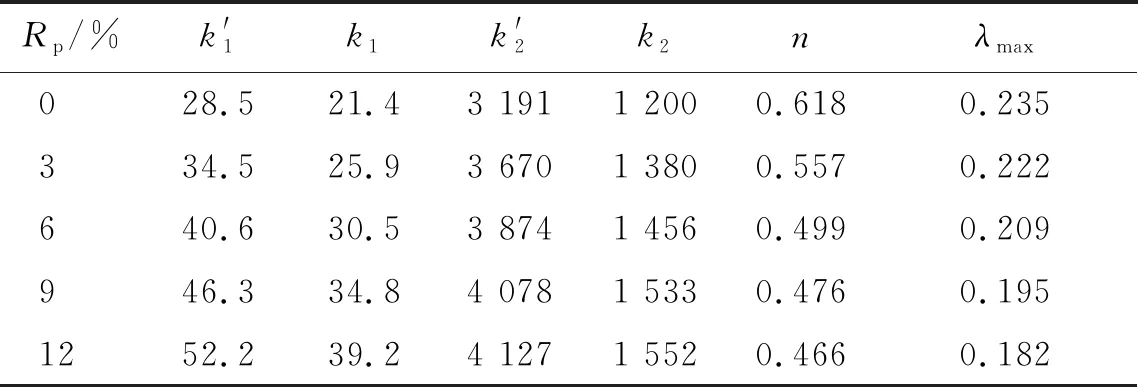
表3 沈珠江动力模型参数表(f=0.33 Hz)

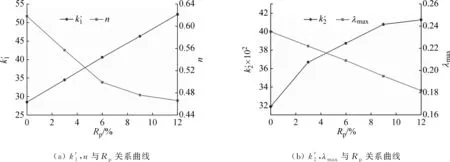
图12 模型参数随高聚物质量比Rp变化的关系曲线

在沈珠江动力模型中，没有考虑高聚物质量比Rp的参数，计算高聚物胶凝戈壁土的动模量和阻尼比时必须对每个Rp下的模型参数进行整理计算，工作量较大。为定量反映高聚物质量比Rp对高聚物胶凝戈壁土动弹性模量和阻尼比的影响，采用经验公式对模型参数和高聚物质量比Rp的关系进行拟合处理，以实现高聚物胶凝戈壁土的动力模型修正。修正后动模量表达式如下

(11)

其中

(12)

(13)

(14)

修正后的等效阻尼比表达式

(15)

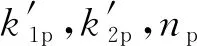
3.3 模型验证

为验证修正沈珠江动力模型对高聚物胶凝戈壁土的适用性，进行了高聚物质量比Rp为0，3%，6%条件下的3组动三轴试验。验证试验固结比Kc为1.5，振动频率为0.33 Hz，围压σ3为0.4 MPa，0.8 MPa，1.2 MPa，每个围压下动应力分7级加载，每级动应力下振动5次。为更接近工程中戈壁土的填筑密实度，试样密度按戈壁土相对密度Dr=0.85(ρd=2.205 g/cm3)控制。

按照沈珠江模型对各高聚物质量比Rp下的试验结果进行整理，得到模型参数；基于天然戈壁土(Rp为0)模型参数，联立式(11)～式(15)，推求出当Rp为3%和6%时的高聚物胶凝戈壁土模型参数，如表4所示。由表4可知，试验结果整理得出的模型参数与采用修正模型预测的模型参数值差异不大，相对误差最大值为5.8%，说明修正模型能较好地描述高聚物胶凝戈壁土在高聚物质量比Rp变化时的模型参数变化，具有较高的精度。

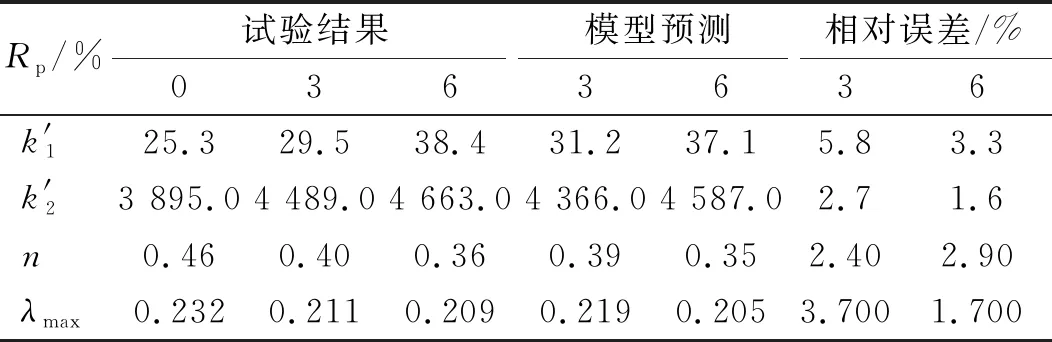
表4 试验和预测模型参数对比

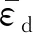
4 结 论

本文通过中型动三轴试验研究了高聚物胶凝戈壁土在标准击实密度、不同高聚物质量比、围压、固结比、加载频率下的动弹性模量和阻尼比的变化规律；在沈珠江动力模型的基础上，建立了适用于高聚物胶凝戈壁土的修正模型，并验证了模型的适用性。主要得出以下结论：

(1) 高聚物质量比Rp对高聚物胶凝戈壁土的动弹性模量的影响较大。在动应力比CSR为0.157时，动弹性模量随Rp增大呈线性增长；CSR>0.157后随Rp增大动弹性模量先增大后减小，当Rp为3%时出现峰值；阻尼比随Rp的增大略有降低。

(2) 在相同CSR下，Rp为0的天然戈壁土经历5周次振动后的残余应变为0.141%，Rp增大，残余应变迅速减小；当Rp为3%时经过5周次振动后的残余应变为0.026%，为天然戈壁土的18.4%。

(3) 当CSR为0.501时，Rp越大，高聚物胶凝戈壁土在循环荷载下产生的应变滞后现象越小，滞回曲线对称性越好，滞回圈面积减小，吸收的能量降低，高聚物的掺入增大了戈壁土抵抗振动荷载破坏的能力。

(4) 基于沈珠江动力模型，建立了考虑高聚物质量比Rp影响的修正沈珠江模型，并与试验结果进行验证，得出修正后的模型具有较好的适用性，可为无试验条件时的动力计算提供经验数据。

(5) 高聚物胶凝戈壁土的动弹性模量随围压和固结比的增大而增大，振动频率对动弹性模量的影响不明显；围压、固结比和振动频率对阻尼比的影响较小。