面向物流提升装备的桁架式立柱刚强度分析

薄澎涛，李 玮，沈 婕

（1.西南林业大学 机械与交通学院，云南 昆明 650224；2.西南油气田分公司 通信与信息技术中心重庆总站，四川 成都 610066）

0 引言

堆垛机是物流运输中运载货物的重要设备，立柱作为该设备的“承重墙”有着不可或缺的地位。堆垛机有单立柱和双立柱两种结构，其结构组成如图1所示，现阶段堆垛机的立柱形式普遍为封闭的腔体，中间穿插有带孔的隔板。立柱的封闭腔体由金属板材焊接而成，制造的形式决定了其有着安装和拆卸不易、维修困难以及结构笨重的缺点。针对上述问题，本文提出了一种新型的桁架式立柱结构，相比于传统的立柱结构，桁架结构具有净空间值高、承受集中载荷效率高、空间扩展性强、设计灵活、易于组装等优点[1]。在拥有这些优点的同时，桁架式立柱也要满足刚度和强度的要求，因此，分析桁架式立柱刚强度对保证其安全性及动力学性能具有非常重要的作用。

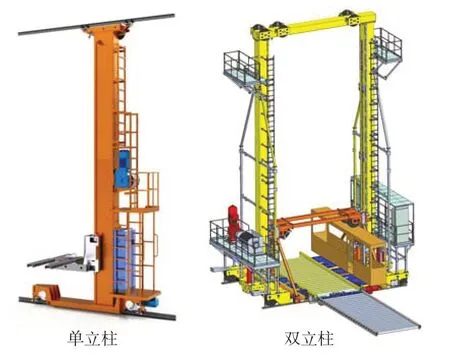
图1 堆垛机

通过有限元分析研究桁架类的结构是一种较为普遍的方法。王春喜，等[2]针对稳定平台测试实验台架，利用MSC软件完成了桁架结构的建模和静、动态特性的分析计算，验证了该结构的轻微震动不影响设备的正常功能。陶友海[3]以黑木沟大桥为例，利用两种软件对挂篮进行数值模拟，分析了不同荷载下的刚强度，并对比了两种软件的适用性，得出了ABAQUS软件更为合理的结论。文铁军，等[4]对桁架结构的通廊分析了风荷载作用于通廊的应力，并提出针对桁架类结构的设计建议。文献[5-7]针对单立柱、双立柱堆垛机的立柱和横梁进行了力学模型的建立和刚强度分析,根据分析结果判断了危险部位，通过给立柱加筋板，在立柱腹板两侧开孔，以及改变立柱的界面尺寸等3种设计，通过实验的方式，对堆垛机结构进行了优化。上述文献多是通过软件作为有限元分析的手段和工具对桁架类结构进行分析，而在没有有限元仿真软件时如何通过理论计算验证桁架类结构的刚强度并未过多涉及。

本文采用NASTRAN对桁架式立柱进行刚强度的有限元分析，验证了其在几种荷载作用下的挠度大小以及应力分布是否符合结构和材料的极限屈服强度。并基于经典小变形弯曲梁理论，探究在没有有限元仿真软件的情况下，为估算桁架式立柱结构承受荷载是否符合工程要求提供了相应的计算方法。

1 桁架式立柱的几何模型

桁架式立柱由底板、顶板、立柱、拉杆以及前后弯折板等连接主体结构的零件组成。图2所示，为桁架式立柱详细的三维模型和各零件的位置关系，由于该模型的高度尺寸较大，中间的模型每层都相同，因此，为了更好地表达零件的细节，相同的模型只展示一部分。除立柱部分的材料采用了6063铝型材外，其余部分均采用Q235B钢材。

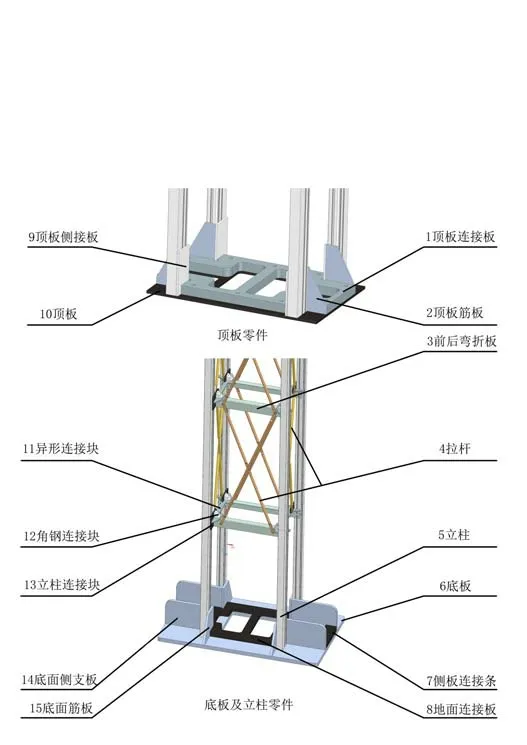
图2 桁架式立柱零件图

2 桁架式立柱有限元分析

有限元分析是一种计算数值的方法，用于确定物理系统的各种物理量，如位移、应力等。它主要基于有限元方法理论和数值解算技术，对复杂的物理现象进行精确的计算求解。有限元分析法在工程学领域应用广泛，可以用于分析和优化各种工程结构、机械装置和材料性质等。

2.1 模型简化处理

有限元分析的简化模型是指通过去除一些细节或者简化复杂结构等方式，将原有的模型简化而得到模型。简化模型的目的是降低计算的复杂度和成本，同时要保证模型的准确性和可靠性。一般而言，在模型简化并建立有限元模型时，应遵循等效刚度原则，即简化后的模型和原模型在刚度上应基本保持一致[8]。也就是说，去掉模型中不显著的项，通过减少项数使模型更容易使用，或者是减少模型的复杂度，使模型更容易计算。考虑到桁架立柱模型的上下底板为固定约束与载荷施加部位，该部位的模型圆角和小孔对刚强度分析几乎没有影响，因此，分析前在NASTRAN中对桁架式立柱模型进行简化处理。

2.2 网格划分

有限元分析的网格划分是将连续的物理对象或区域离散化为一系列离散元素的过程。网格划分是有限元分析中最重要的步骤之一，它直接影响到有限元分析的结果精度和计算效率，网格的划分是有限元模型建立的基本要求。1D单元用于描述两个节点之间直线或曲线结构的刚度，主要应用于梁、桁架、加强筋、网格连接等结构，表1列出了NASTRAN中部分1D单元的类型和用途。

表1 1D单元的类型

模型立柱部分截面的剪切中心不与中性轴重合，因此采用复杂梁单元的CBEAM单元，在梁截面管理器中定义立柱截面。拉杆的截面需要根据不同的拉杆位置定义不同的截面，拉杆的两端、中间部位、完整拉杆截面以及赋予3种截面的单根拉杆如图3所示。

图3 拉杆不同部位截面图

2D单元也称面单元，用于表示相对于其他维度单元厚度较小的一种结构。在桁架式立柱的前后弯折板、异形连接板和立柱连接块3个零件部位，其模型的厚度远小于长度和宽度，因此，将这三种零件抽取中面，并定义其厚度和材料，采用2D单元进行网格划分来代替3D实体网格划分，以减少后期网格数量和计算量[9]。除上述模型外，其余模型采用3D单元进行划分，桁架式立柱模型零件均为规则的几何模型，所以在划分网格时，使用性能完善的自适应划分网格,即系统根据模型的具体情况决定单元的大小进行网格划分[10]。

划分网格的过程中需要定义单元材料，表2为所用到的两种材料的物理属性。

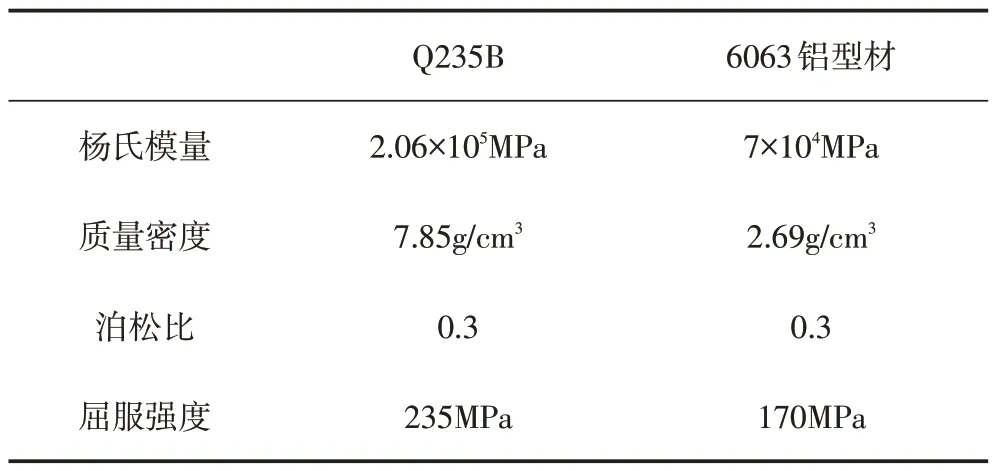
表2 材料物理属性表

建立好的整体有限元模型如图4所示，共产生了409 379 个单元和518 096 个节点，其中，1D 单元共有22 396 个，2D 单元共有106 055 个，3D 单元共有106 584个。通过单元质量的检查，大部分单元的雅可比、宽高比、锥度、实体翘曲和边点夹角等单元属性都符合要求。桁架式立柱的高度有近2×104mm，模型中间重复的部分并没有全部展示，并附上部分单元的细节局部放大图。

图4 网格划分结果和细节图

2.3 连接关系和边界条件

完成网格划分后，各个零部件之间还需建立对应的连接关系，上下底板的零部件之间和立柱与底板之间为焊接，采用1D连接中的面-面方式即可实现零部件之间的焊接，需要注意的是立柱的1D连接所选择的连接节点应全部处于立柱截面的形状区域。桁架式立柱中间部分的连接主要以螺栓连接为主，由于立柱部分采用的是1D单元划分的网格，立柱与中间零件的连接采用1D单元的节点与零件孔进行连接。螺栓孔之间采用RBE2单元蛛网连接。定义螺栓的连接中需要建立点到点、点到边等节点连接，这些节点的选择先后决定了其属性为独立节点还是依附节点，假设两个孔之间的点到边连接圆心点为独立节点，孔边节点为依附节点，而两个圆心点在建立连接时则会产生圆心点既是独立节点，也是依附节点的矛盾，如图5所示，这就发生了节点的属性冲突。若要解决这种冲突，须在解算方案的模型数据参数中将AUTOMPC更改为允许，这样NASTRAN会根据模型情况自动判断节点的独立依附关系。

图5 独立节点和依附节点

完成有限元模型的建立后，根据桁架式立柱的实际工作需求定义边界条件，创建包含4种工况的解算方案，表3为边界条件施加的详细情况。

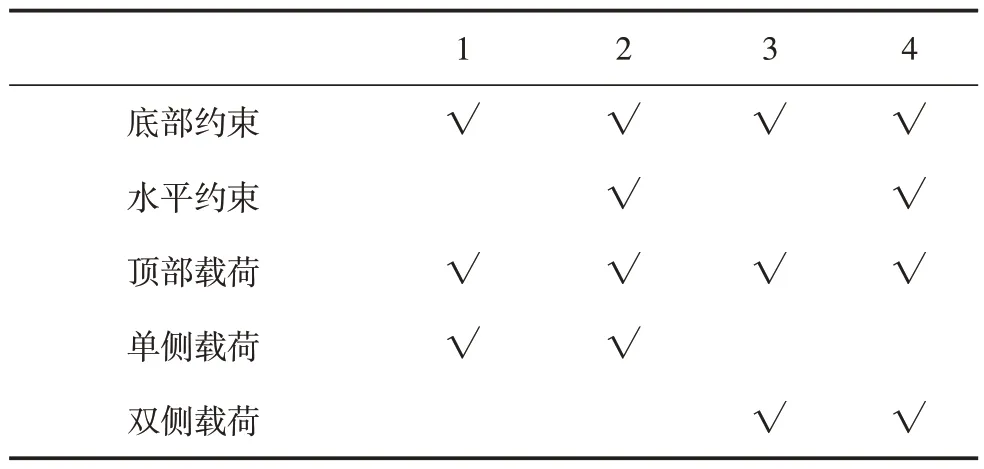
表3 边界条件

图6所示为4种工况的设定图例：

图6 工况预设图

工况一：固定立柱底部，顶部两个130mm×49mm的长方形范围内施加4 740N的力，方向竖直向下，在立柱内侧距顶部600mm、1 400mm的位置施加一对方向相反的3 087N的力。

工况二：在工况一的基础上，每间隔一组横梁施加一个水平约束。

工况三：在工况一的基础上，在对侧对称施加相同大小的力。

工况四：在工况三的基础上，按照工况二对横梁进行固定。

2.4 有限元分析结果

依据上述4种工况定义解算方案中的边界条件并求解，得到4种工况下的应力云图，如图7所示。

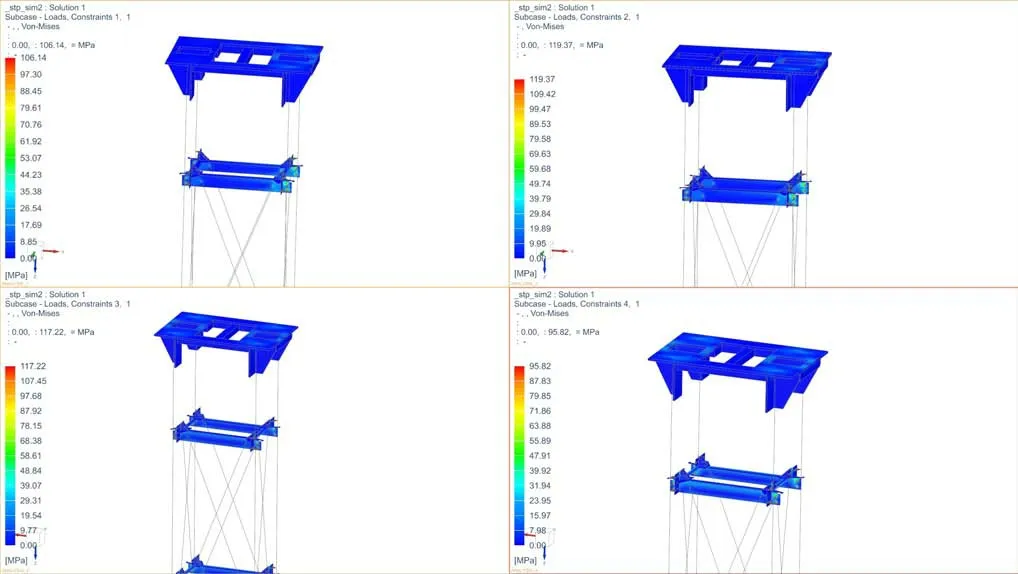
图7 4种工况下的应力云图

立柱部分的应力均取应力最大值，依据圣维南原理，如果把物体局部边界上的力系，使用分布不同但静力等效（主矢相等绕任一点的主矩也相等）的力系来代替，则这种等效处理使得物体的应力分布仅在作用区域附近有显著影响，而在远离作用区域的地方所受到的影响很小，可以忽略不计[11]。因此，为得到正确的应力值，立柱截面取一半高度的位置，即l=9 821mm。立柱截面的应力云图如图8所示。

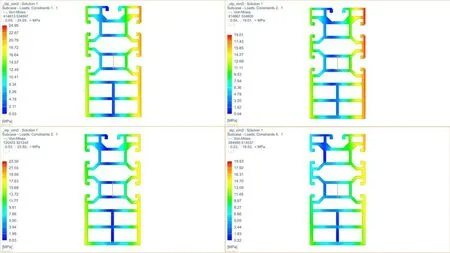
图8 4种工况下立柱截面的应力云图

4种工况下桁架式立柱所产生的最大应力都小于两种材料的许用应力，满足实际工作中的使用要求，表4为4种工况下的应力对比情况。

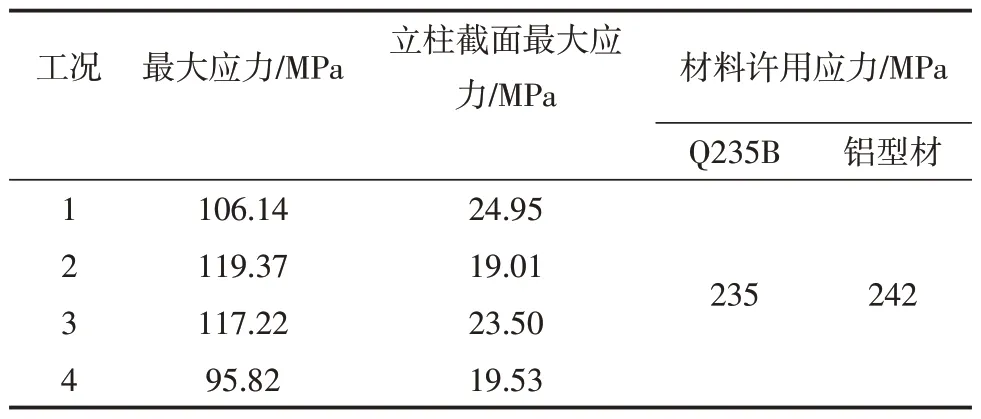
表4 四种工况应力对比

3 基于经典小变形弯曲梁的计算

3.1 整体截面抗弯刚度的确定

惯性矩是一个几何量，通常被用作描述截面抵抗弯曲的性质。桁架式立柱的立柱截面为复杂截面，若要计算整体的挠度就需要计算桁架式立柱整体截面的惯性矩，4根立柱的截面一致，在得出单个复杂截面的惯性矩后，可以通过移轴定理得出4个截面关于整体模型中性轴的惯性矩。

整体立柱模型截面形状及尺寸关系如图9所示。

图9 整体截面图

由于立柱截面的形状复杂，其面积计算起来较为复杂，因此，可以通过软件直接得出此截面的面积及惯性矩Iyc，本文直接采用软件内所给出的准确数据。

在得到单一截面对其中性轴的惯性矩之后，通过平行轴定理计算出每个截面对整体模型中性轴的惯性矩。查阅相关资料得到平行轴定理公式：

其中：Iy：截面对整体中性轴的惯性矩；

Iyc：截面对自身中性轴的惯性矩；

a：截面中性轴到整体中性轴的距离；

A：立柱复杂截面的面积。

代入数据可得：

Iy=4.47×105+2852×1 666.45=1.36×108mm4

则模型总的惯性矩为：

I总=4×Iy=5.44×108mm4

材料的杨氏模量E 在表2 中已给出，E=7×104MPa，桁架式立柱的整体抗弯刚度为：

EI总=7×104×5.44×108=3.8×1013MPa·mm4

3.2 桁架式立柱的挠度与应力

3.2.1 最大挠度。挠度是在受力或非均匀温度变化时，杆件轴线在垂直于轴线方向的线位移或板壳中面在垂直于中面方向的线位移。本文所述的桁架式立柱的立柱部分为一等截面体，即EI为一定值。根据作用于立柱上的边界条件，可以将桁架式立柱看作为一端固定，另一端施加荷载的悬臂梁，如图10所示。

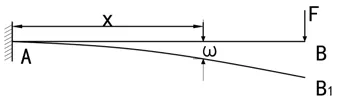
图10 桁架式立柱等效图

上述悬臂梁的弯矩与曲率关系为：

曲率又可表示为：

这里略去了式（3）曲率表达式中分母的高阶项，因此，该理论只适用于小变形弯曲梁，联立式（2）和式（3），得到挠曲线近似微分方程为：

对上式进行两次积分，得：

其中x处的弯矩方程为：

由于A处施加了固定约束，在A截面处，桁架式立柱的挠度为0，代入式（5）中得到C=0，D=0。因此，桁架式立柱的挠曲线方程为：

桁架式立柱在力的施加处取得挠度的最大值，即x=l=19 642mm。将桁架式立柱的各项数据带入式（7）中即可计算出端点B处的最大挠度fmax的值为：

3.2.2 最大应力。通过查阅相关资料[12]得到立柱弯曲正应力求解公式为：

将数据代入式（8）中得到立柱截面的应力为：

4 分析结果对比

在桁架式立柱顶端的侧面施加一大小为3 000N的横向力，底面施加固定约束，忽略重力，模拟悬臂梁理论计算模型，得到仿真计算结果。有限元仿真的挠度和应力结果如图11所示。

图11 仿真结果

在顶端3 000N 横向力的作用下，桁架式立柱最大的挠度为181.07mm，相较于理论计算结果199.42mm 有9.20%的误差。立柱中间位置截面的应力理论值为16.79MPa，与仿真应力结果16.05MPa 相比有4.4%的误差。

在上述理论计算过程中，并未考虑桁架式立柱的拉杆部分，拉杆部分的存在会增大桁架式立柱整体的抗弯刚度，这也是理论计算结果比仿真结果大的原因。若将拉杆截面的惯性矩为2 700.98mm4，代入式（1）计算得到拉杆截面对整体中性轴的惯性矩为：

Iy=2 700.98+2662×59.69=4.2×106mm4

拉杆的杨氏模量为E=2.06×105MPa，则拉杆部分总的抗弯刚度为：

4EIy=4×2.06×105×4.2×106=3.46×1012mm4·MPa

将其代入式（5）和式（6）中得到桁架式立柱的最大挠度和中间截面的应力分别为：

对比结果见表5。

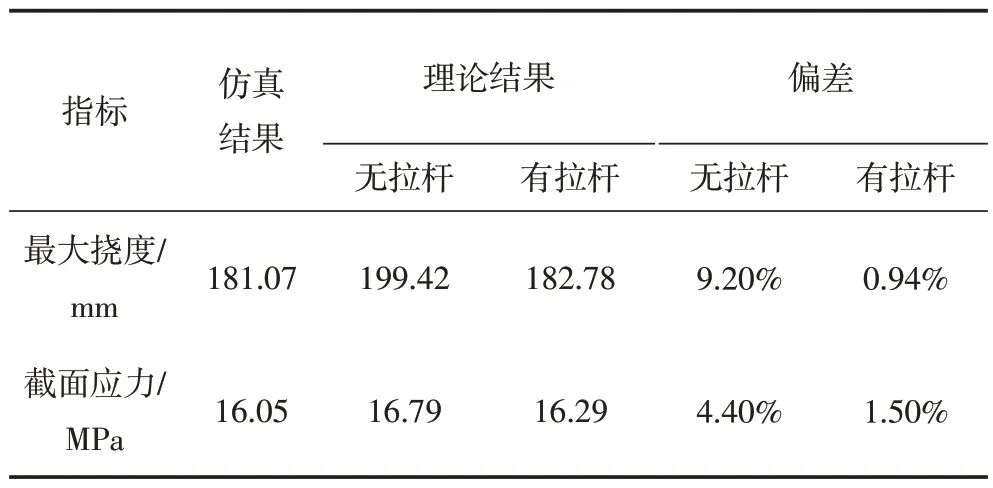
表5 理论与仿真结果对比表

综上，在实际工程应用中，此类桁架式结构可以按照上述理论方法简单验证其在承受荷载时产生的变形是否符合工程需求，这为未能采用有限元仿真软件时提供了一种行之有效的理论计算方法。

5 结语

本文主要以堆垛机为例，分析了物流提升装备传统立柱结构存在的一些问题，针对这些问题，提出了一种新型的桁架式结构。采用有限元分析方法，对桁架式立柱的整体结构进行了静力学上的刚强度分析。在得到最大挠度和立柱截面应力的仿真数据后，基于经典小变形弯曲梁理论阐述了一种理论上的计算方法。在对比两种方法得出的结果后，加入桁架的拉杆结构对整体刚度的影响，互相验证了两种方法的可行性，为桁架式立柱后续的设计与优化提供了参考。本文采用的研究方法对于其他类似产品部件的有限元分析也具有较好的借鉴意义。